线性回归
1 一元线性回归
线性回归具有如下性质
y = x[0]w[0]+x[1]w[1]+…+x[m-1]w[m-1]+w[m]
其中w[0],w[1]…w[m-1],w[m]是m+1个权重值
线性回归是假设自变量和因变量之间的关系有这样子的形式,再利用数据确定出这m+1个权重值,最终找到自变量和因变量之间的关系。
1.1 最小二乘法
? 最小二乘法(Linear Least Squares, LLS) 是一种最基本的线性回归方法。在最小二乘回归中,有n条数据,每条数据有m个自变量数值x[i,0],x[i,1],…x[i,m-1]和一个因变量数值y[i],0<=i<n,一般情况下n>>m,即数据的条目远大于自变量的个数,因变量的个数等于数据的条目。在机器学习领域,数据条目中的自变量的数值又称为 “特征”(feature) ,因变量的数值成为标签(label)。用张量记号,可以把所有的数据条目的特征和标签分别记为一个张量。
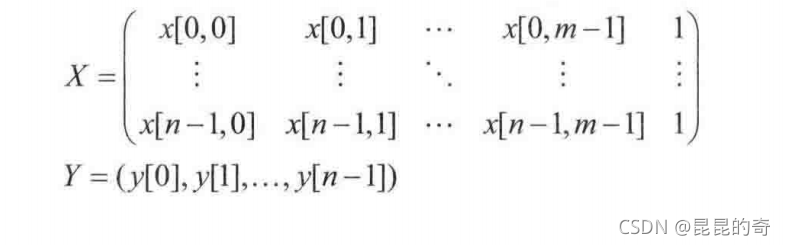
? 如果特征和标签之间完全由W指定的线性关系精确确定,则有y[i,:] = X[i,:]·W。若以上等式对所有条目都成立,则有Y = X·W
。线性回归,就是试图找到权重值W,使得Y和X·W尽可能接近。
? 最小二乘法用均方误差(Mean Squared Error,MSE),表示Y和XW的接近程度,均方差的表达式为:

? PyTorch中的函数torch.lstsq() 实现了最小二乘法。这个函数有两个参数,分别对应了MSE里的张量Y和X。这个函数有两个返回值,前一个返回值包括了所有的权重值,后一个返回值是QR分解的结果。当X的大小为 (n,m+1) ,Y的大小为 (n,),这个返回值是一个大小为 (n,1) 的张量(这是个 二维张量)。取这个张量的 前m+1 个元素,可以得到大小为 (m+1,) 的张量w。(这个张量的其他元素是表示残差的量,平方和就是MSE的值)
demo
import torch
x = torch.tensor([[1., 1., 1.], [2., 3., 1., ], [
3., 5., 1., ], [4., 2., 1.], [5., 4., 1.]])
y = torch.tensor([-10., 12., 14., 16., 18., ])
wr, _ = torch.lstsq(y, x)
w = wr[:3]
print(w)
1.2 正规方程法
? 正规方程(normal equation) 法是最常见的求解最小二乘法的方法。推导过程略。
? 正规方程表达式:

? 方程的解:

2 多元线性回归
? 多元线性回归试图讨论自变量与多个因变量之间的关系。我们可以逐一考虑自变量和每一个因变量之间的关系,建立多个线性回归问题来求解。但是我们也可以将多个线性回归问题合并成一个问题来一次求解
? 设自变量有m 个(不包括常数1),因变量有c个,则特征张量 X的大小为 (n,m+1),标签张量Y的大小为 (n,c),这时候的权重张量的大小为(n,c),用torch.lstsq()求解同一元线性回归。
demo
import torch
x = torch.tensor([[1, 1, 1], [2, 3, 1], [3, 5, 1], [
4, 2, 1], [5, 4, 1]], dtype=torch.float32)
y = torch.tensor([[-10, -3], [12, 14], [14, 12],
[16, 16], [18, 16]], dtype=torch.float32)
wr, _ = torch.lstsq(y, x)
w = wr[:3, :]
3.其他损失情况下的线性回归
? 接下来用梯度下降法求解线性回归问题。为了叙述方便,将一元线性回归看成多元线性回归的特殊情况。
3.1MSE损失、l1损失和平滑l1损失
? 假设结果预测张量Z(W)=X·W。预测结果张量Z的大小和标签张量Y的大小相同,其大小为**(n,c)** ,Y的元素个数是n’
(1)MSE损失又称l2损失。预测结果Z和标签张量Y的MSE损失为

? (2)l1损失又称 “平均偏差”(Meaning Absolute Deviance,MAD)。预测结果Z和标签Y的l1损失定义为
? 
? (3)平滑1范数损失(smooth l1 Loss) 又称为Huber损失。预测结果Z和标签Y的损失定义为:
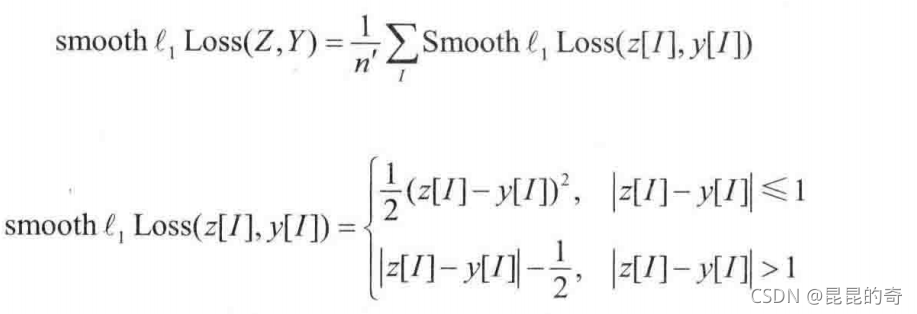
? 如果交换预测结果Z和数据标签Y的位置,损失值不变。这样的损失为对称损失。但是,无论损失是不是对称的,在定义和使用的过程中,都必须把预测结果Z写在前面,把数据标签Y写在后面。这是因为,预测结果和数据标签在损失中的地位不对等,预测结果需要对张量W求梯度,而数据标签不需要对张量W求梯度。
3.2 torch.nn子包与损失类
PyTorch已经在torch.nn子包中实现了多种损失。
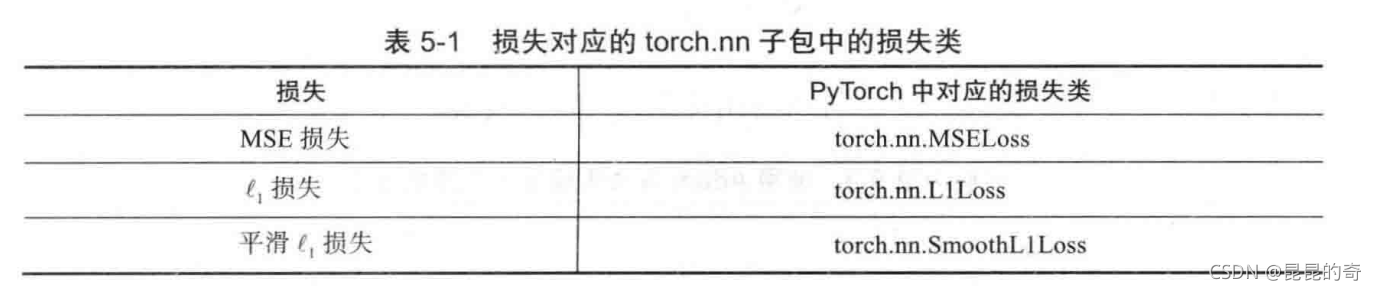
? torch.nn里的损失类都是torch.nn.Module类的子类。要使用torch.nn.Module类的子类,需要构造并调用类实例。具体的使用方法如下。
-
根据损失类型选择torch.nn子包中对应的类。一种损失对应着torch.nn包中的一种损失类。
-
使用选定的损失类构造类的实例。
demo
criterion = torch.nn.MSELoss() -
调用类的实例,并以预测结果和标签作为参数。这两个参数都是张量类型。需要注意的是,要先用预测结果作参数,再用标签做参数。
demo
pred = torch.arange(5,requires_grad = True) #预测结果,对应X·W y = torch.ones(5) #标签 loss = criterion(pre,y) -
利用调用类得到的损失值进行后续操作,如求梯度,优化等。
demo
loss.backward()
3.3 使用优化器求解线性回归
? 无论什么损失都可以用梯度下降法找到合适的权重W,使得损失最小。采用这种方法,需要先实现损失,然后对损失求梯度,并据此更新迭代W的值。事实上,即使是MSE损失,当数据过多而不能一次性全部载入内存时,也可以采用梯度下降法,在每一次迭代时选择载入一部分数据进行运算。
? 这个方法与torch.lstsq()相比更加费时费力,运行时间也更长。对于torch.lstsq()函数能解决的问题尽量用torch.lstsq()函数解决。
import torch
x = torch.tensor([[1, 1, 1], [2, 3, 1], [3, 5, 1], [
4, 2, 1], [5, 4, 1]], dtype=torch.float32)
y = torch.tensor([-10, 12, 14, 16, 18], dtype=torch.float32)
w = torch.zeros(3, requires_grad=True) # 初始化为0
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam([w, ])
for step in range(30001):
if step:
optimizer.zero_grad()
loss.backward()
optimizer.step()
pred = torch.mv(x, w)
loss = criterion(pred, y)
if step % 1000 == 0:
print(f'step = {step}, loss = {loss:g}, W = {w.tolist()}')
? torch.nn子包中的torch.nn.Module 扩展类除了包括各种损失类,还有torch.nn.Linear类。torch.nn.Module类包括一些可以求梯度
的张量(在touch.nn.Linear类中,那些可以求梯度的张量就是线性组合使用的权重张量) touch.nn.Linear类的使用方法遵循touch.nn.Module类的使用方法,需要构造并调用类的实例。在构造torch.nn.Linear类的实例时,需要提供两个int型参数。在线性回归的语义下,这两个参数相当于特征的个数(包括常量1,因此有m+1个)和因变量的个数(即c) 。还有一个关键字参数bias ,它的默认值时True。关键字参数bias表示是否考虑偏移(bias)
? torch.nnModule类实例还有个成员方法parameters(),它返回一个张量的生成器(generator),它可以生成这个模块涉及的所有可导张量。torch.nn.Linear类实例在bias=True的情况下,parameters()返回的生成器可以生成一个大小为(m,c)的权重张量和大小为(c,)的偏移张量
用torch.nn.Linear(),就不用显式地定义权重张量W。这个类的实例中就包含了权重张量。而且对于这里的特征张量不需要再补齐没有意义的1,因为使用了torch.nn.Linear类并对偏移进行了特殊处理。
demo
import torch
x = torch.tensor([[1, 1], [2, 3], [3, 5], [4, 2], [5, 4]], dtype=torch.float)
y = torch.tensor([-10, 12, 14, 16, 18], dtype=torch.float).reshape(-1, 1)#一定要reshape否则后面数据不一致,大小为(-1,c)
fc = torch.nn.Linear(2, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(fc.parameters())
weights, bias = fc.parameters()
for step in range(30001):
if step:
optimizer.zero_grad()
loss.backward()
optimizer.step()
prediction = fc(x)
loss = criterion(prediction, y)
if step % 1000 == 0:
print( f"step = {step}, loss = {loss:g}, weights = {weights.tolist()}, bias ={bias.item()}")
3.4 数据的归一化
? 在某些线性规划问题中,特征的数值范围和标签的数值范围差别很大,或者不同特征之间的数值范围差别很大。这时,某些权重值可能会特别大,这为优化器学习这些权重值带来了困难。在这种情况下常常对数据进行归一化,使得优化器面对的每个特征的数值或标签的数值在一个相对固定的范围内。
? torch.mean()函数和torch.std()函数可以用于求张量的均值和方差。利用这两个函数可以把某个特征或标签A归一化为

? 归一化得到的特征或标签的均值为0,方差为1。这样它们的取值范围就相对固定了。
下面demo对有无归一化进行了对比。程序输出了迭代过程中的损失。这里的损失都是原数据下的统计结果,与是否归一化没有关系。统计结果表明,对数据进行归一化后,损失下降的更快了。
demo 没有归一化
'''在没有数据归一化的情况下进行线性回归'''
import torch
x= torch.tensor([[1000000,0.0001],[2000000,0.0003],[3000000,0.0005],[4000000,0.0004],[5000000,0.0004]])
y = torch.tensor([-1000.,1200.,1400.,1600.,1800.,]).reshape(-1,1)
fc=torch.nn.Linear(2,1)
criterion= torch.nn.MSELoss()
optimizer = torch.optim.Adam(fc.parameters())
for step in range(10001):
if step:
optimizer.zero_grad()
loss.backward()
optimizer.step()
prediction = fc(x)
loss= criterion(prediction,y)
if step%1000 ==0:
print(f"step = {step}, loss = {loss:g}")
demo 有归一化
'''借助数据归一化进行线性回归'''
import torch
x = torch.tensor([[1000000, 0.0001], [2000000, 0.0003], [
3000000, 0.0005], [4000000, 0.0004], [5000000, 0.0004]])
y = torch.tensor([-1000., 1200., 1400., 1600., 1800., ]).reshape(-1, 1)
x_mean, x_std = torch.mean(x, dim=0), torch.std(x, dim=0)
x_norm = (x-x_mean)/x_std
y_mean, y_std = torch.mean(y, dim=0), torch.std(y, dim=0)
y_norm = (y-y_mean)/y_std
fc = torch.nn.Linear(2, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(fc.parameters())
for step in range(10001):
if step:
optimizer.zero_grad()
loss_norm.backward()
optimizer.step()
prediction_norm = fc(x_norm)
loss_norm = criterion(prediction_norm, y_norm)
prediction = prediction_norm*y_std+y_mean
loss = criterion(prediction, y)
if step % 1000 == 0:
print(f"step = {step}, loss = {loss:}")
? 在用优化器求解线性回归的权重时,对各特征和标签进行归一化非常重要!!!