一、监督学习、无监督学习
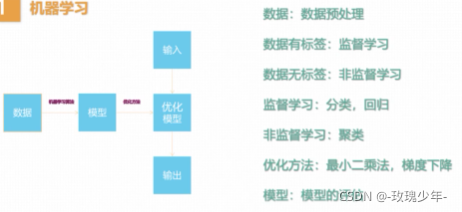
二、特征工程
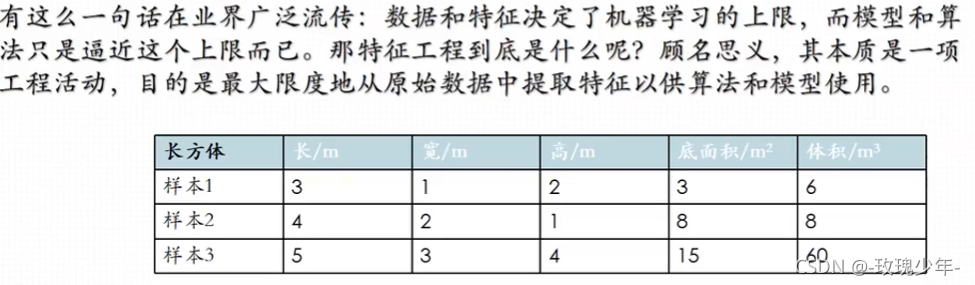
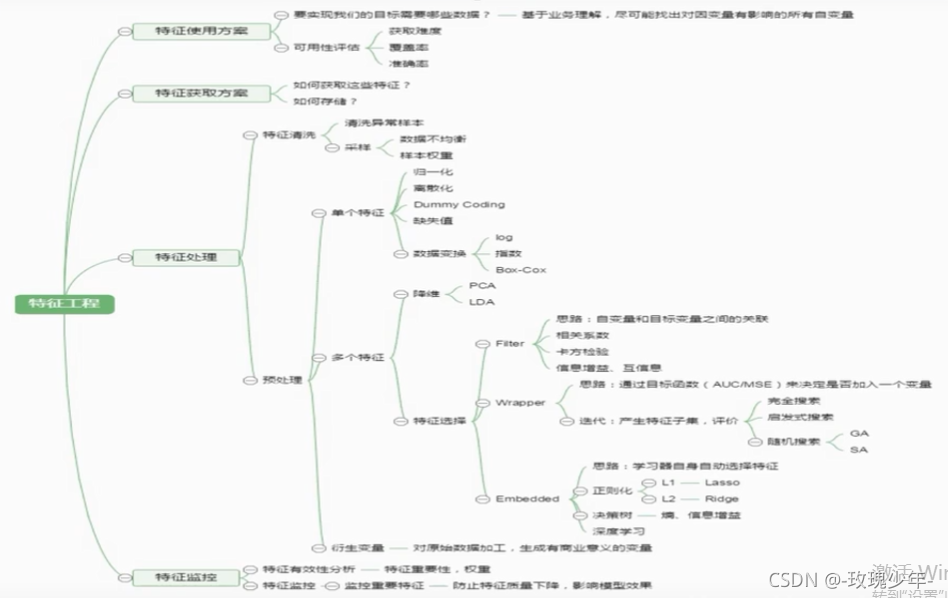
三、特征选择
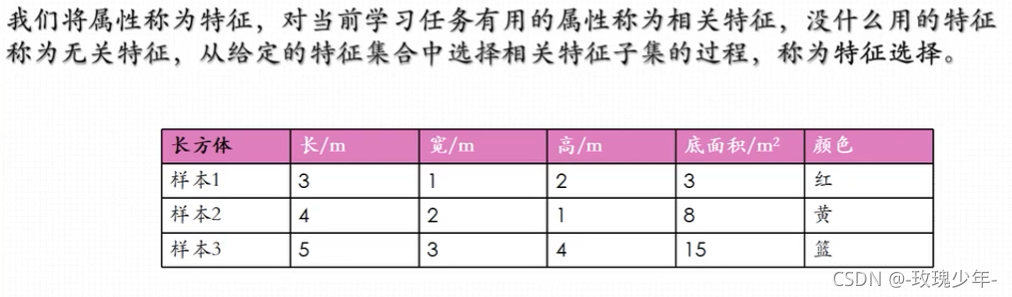
显然,以上属性中“颜色”这个属性是无关特征,而长宽高就是相关的特征。
为什么进行特征选择呢?
1、冗余。
我们在现实任务中经常会遇到维度灾难问题,这是由于属性过多造成的。假如我们从中选出重要的特征,就可以使得在之后的学习过程中只需要在一部分特征上构建模型,维度的灾难问题就会大幅度减轻。
去除不相关的特征,比如上图的颜色特征,抽丝剥茧,只留下关键的因素。这样我们就更容易看清楚。
2、噪声。
数据集中有些数据不仅对你选择分类模型没有正向的影响,反而可能有负的影响。
特征选择和降维的区别·:
前者是去掉原本特征里和结果预测不大的。
后者做特征的计算组合构成新特征。
举例:
任务:求长方体的体积
特征1:长、宽、高、底面积
特征2:长、宽、高
结果特征集:高、底面积
特征1—>结果特征集属于特征选择,因为只是筛掉了长、宽两个特征。
特征2—>结果特征集属于降维,因为底面积是从长、宽两个特征降维得来的。
特征选择三大类型:
1、过滤型
按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征。
缺点:没有考虑到特征之间的关联作用,可能把有用的关联特征误剔除掉。
发散性其实就是用方差的方式来选择、过滤特征。
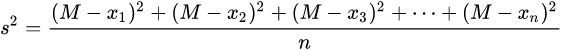
设置阈值为d,当方差>=d,就保留此特征,<则删除。
相关性,计算相关性的方法很多,如:皮尔逊系数,一些距离系数等。
接下来介绍一种贝叶斯方法来分析特征之间的相关性。
贝叶斯公式:
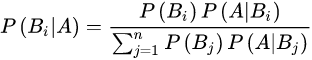
在A发生的条件下,Bi发生的概率 =
分子:Bi发生的概率Bi发生的条件下A发生的概率
分母:j从1+到n,Bj发生的概率Bj发生的条件下A发生的概率
简化思路,去A的路有B1、B2…Bn中方式,
在去到A后,求从B1出发的概率是多少?
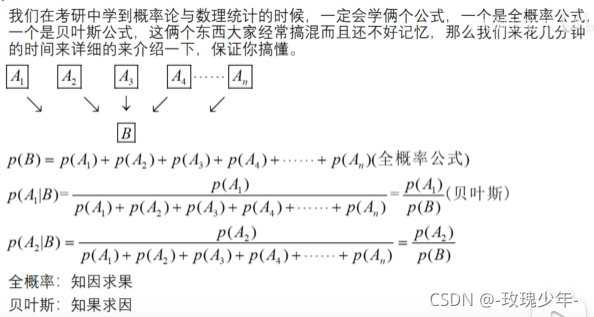
来看一个选好瓜的例子:



同样,我们取阈值d,当式子>=d时,就把Xi保留下来,否则删除。
例如上图选瓜图中,x3是最好的特征,可以把x1,x2都删除掉。
2、包裹型
把特征选择看做一个特征子集搜索问题,筛选各种特征子集,用模型评估效果。
经典算法:
递归消除特征法:使用一个模型来进行多轮训练,每轮训练后,移除若干权值系数的特征,再基于新的特征集进行新一轮的检测。
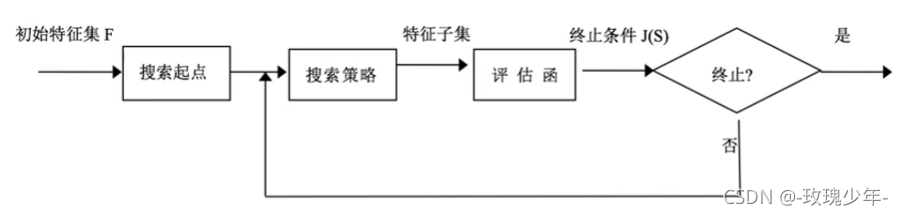
搜索策略:
a.前向搜索:初始特征集F为空,加特征,利用评估函数来测定,假如达到了要求,就终止,如果没有达到要求,就继续循环。
b.后向搜索:初始特征集F={x1,x2,x3…xn},删特征
c.随机搜索算法:从初始集{x1,x2,x3…xn}中随机的选若干特征如{x1,x5,x6…xn}
其实我们要做的就是在初始特征集F里面选出字节和S,由于F的维度是n,如果用穷举法算的话,可能需要算2^n-1次,显然搜索次数太多,所以就需要选取响应的搜索策略。
终止条件有四种:
1、比如F有100个特征,筛选够50个就停止。
2、搜索循环的次数超出了给定的阈值,比如100次的时候就停止。
3、评估函数已经达到最高或者最优,停止。
4、评估函数超出预先给定的阈值,比如打分,分数到达80分即可,那我们到达80就停止。因为一直要特征值最高或者最优是可遇不可求的。
模型评估:
1、ROC曲线
2、AUC,AUC是ROC与x轴的面积,AUC越大说明模型越好。
2、嵌入型
根据模型来分析特征的重要性
利用正则化思想,将部分特征属性的权重变为0。(正则化是防止过拟合的)
包裹型算法一直在迭代,所以它的时间复杂度较高,如果有上亿维度的特征,用包裹型就不太现实。
嵌入式在训练的过程中就把不需要的特征权重置为0了,但嵌入式删掉的不一定都是不好的特征,可能两个很好的特征它只保留了一个,但是它可以很好地降维。
嵌入式算法适用于维度很高的情况。