前章回顾
在ch03中我们做了一个有趣的任务,就是做一个手写数字的分类。
我们的数字包含了0~9共10类,于是我们的第一思路是训练出10个二元线性分类器。
我们用一个大矩阵来存储每个线性分类器拟合出来的Theta,大矩阵的某一行就是专门为某一数字拟合出来的系数,当我们的原数据对应与系数相乘并且经过激活函数sigmoid之后就会得到属于此数字类别的概率。
同时我们初步认识了神经网络,知道其能去学习一些非线性的特征,其中的隐藏层hiddenlayers利用的是不再是我们直接喂入的数据了,最后的正确率十分可观。
我们简单实现了前向传播的过程,无非就是包含了加入一列偏置项和矩阵相乘的运算。
神经网络的损失函数
因为我们同样是在利用神经网络进行一个分类的任务,所以其损失函数的公式实际上是和逻辑回归的损失函数类似的。如下图所示:

可以看到其中的交叉熵损失函数和正则项都是完全相同的。
其中在交叉熵损失函数处我们多了一个K求和,这里就要牵扯到一个one-hot独热编码的概念。
因为在手写数字分类任务中,我们的神经网络最后会输出10个值,每个值分别代表属于某一个数字的概率。但我们的标签只有一个值,就是数字本身(0除外,其标签我们设置成了10)。此时我们需要对标签进行一个处理,比如标签9,变为一个向量:
[0,0,0,0,0,0,0,0,0,1],就是把对应的下标设置为1即可。
同样可以从概率的角度理解,即其为9的概率为1,其他值的概率为0!
所以这个K求和就是在说要为每一个预测出来的概率做交叉熵。
你可以这么想,比如一些奇奇怪怪的人写6和0很像。
此时对于标签来说,6的概率为1而0的概率为0。
但神经网络不这么想,他可能认为是0的概率也有高达40%,只不过它认为是6的概率更高,这样一来,argmax的时候仍旧能正确预测是6,但无疑在0这个标签上就存在了误差。所以我们的误差要对K个标签做求和处理!
接下来就是正则项,这个并不难理解,同样是把所有theta都进行了惩罚!只不过theta的下标比较多而已…所以才会有当前看到的3重求和运算,以我们的作业的神经网络为例:
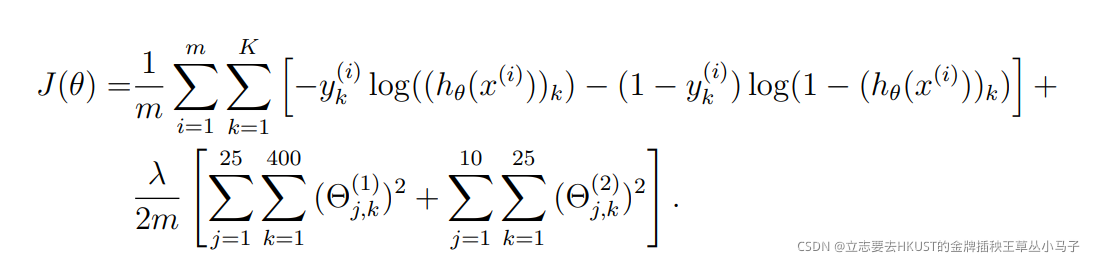
因为我们的输入层是400个神经元,隐层是25个神经元,输出层是10个神经元。
而且我们的网络又是全连接的,即两层之间的神经元都是互相连接着的,两两神经元间连着的线就是一个权值theta,所以含义很简单,就是全部的theta做一个正则惩罚处理。
从第一个公式的普适性上来讲,简要进行分析:
l控制层数,共L层的话就是有L-1个映射关系需要用到theta。
i控制当前层的神经元个数,sl就是当前层的所有神经元的总数。
j就是控制下一层的神经元个数。
要具体的表现一个权值我们需要告知这三个参数,即某一层的第几个神经元与下一层的第几个神经元相连接。
好了,有了损失函数,我们又可以通过梯度下降或者更加高阶的优化算法来进行缩小损失的步骤了。
这也是神经网络中最困难的部分,用到了“链式求导”法则。以后再进行“深度学习”时同样会遇到“计算图”、“反向传播”的概念,下一部分我可能写得并不是特别好,需要配合视频+推荐的两篇推导博客进行服用达到好的效果。
反向传播算法
反正我一开始看视频是没看懂的,我看了另外两篇博客才慢慢推导出来反向传播究竟在干什么。这里附上两个链接:
反向传播算法推导1
反向传播算法推导2
反向传播其实就是我们求导的一个过程,我们最终的目的同样是需要用损失函数J对theta进行求导然后不断缩小损失值提高精确率。
但看起来用这个巨麻烦的损失函数直接对theta进行求导并不是件很好办的事儿!
why?你想想你输入层映射到隐层的theta值并不是直接对损失函数直接造成影响的值啊,只有隐层直接到输出层的theta才会在损失函数中被直接用到。
正因如此我们才会用到链式求导。
好,这里简要说了为什么会需要链式求导,接下来我们需要定义一个中间量。
名为δ(delta),其有一个上标l代表层数,下标j代表第几个神经元。
其数学定义如下:
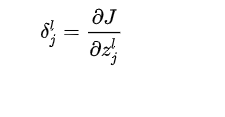
这里的z就是未经sigmoid激活之前的值而已。
这里我们先对输出层进行简单分析:
(这里就以一张图的输入为例,也就是先不考虑m的影响)
我下面写得那个“觉得多余”完全基于这是输出层,其它层肯定得考虑完整!

再对前面的层进行分析:

结局完我们的中间变量,再去回归正题,因为我们仍旧是做的对theta进行求导!
theta求导其实就是大同小异了,同时不难发现我们所计算的δ在这儿都用得上。

不知道自己推得咋样。。但是第一篇知乎大佬的公式会整洁很多!
作业代码
因为这次的神经网络我用的是类,所以里面会带个self。
1.数据可视化。
def displayData(self):
Data = loadmat("./ex4data1.mat")
self.X = Data['X']
self.length = len(self.X)
self.labels = Data['y'].reshape(-1) # it's not very convenient to label image 0 with 10
self.labels -= 1 # it's the way that we use
self.Y = self.labels.copy()
show_indexes = np.random.randint(0, len(self.X), 100)
for i in range(len(show_indexes)):
plt.subplot(10, 10, i + 1)
plt.axis(False)
plt.imshow(np.transpose(self.X[show_indexes[i]].reshape(20, 20)))
plt.show()
可视化和ch03是一样的,这里不再具体解释。
2.模型的表示,载入weights,可以固定下Theta1和Theta2的shape,同时可以在写完损失函数后和老师给出的损失值做一个对比以确保正确性。
很简单,不打算解释:
我这里直接给出了theta的shape。
def loadRandomInitializedParameters(self):
Thetas = loadmat("./ex4weights.mat")
self.theta1 = Thetas['Theta1']
self.theta2 = Thetas['Theta2']
# after debugging, you'll find the shape of two matrices
# size of theta1 is (25, 401) while the other is (10, 26)
# well, on the other hand, the size of our training data X is [5000, 400].
# clearly, before we multiply, add a bias column in X first
3.前向传播和损失函数。
前向传播实际上我们在ch03也写过了,几个关键步骤就是加一列偏置项,做矩阵相乘的运算,sigmoid激活函数。
def sigmoid(X):
# sigmoid activation function
return 1 / (1 + np.exp(-X))
def forwardPropagation(self):
bias = np.ones((len(self.X), 1))
# first we should implement the feedforward propagation
# here we use a to represent values after sigmoid while z before..
a1 = np.hstack((bias, self.X)) # size is (5000, 401)
z2 = np.dot(a1, self.theta1.T) # size is (5000, 25)
a2 = sigmoid(z2) # size is (5000, 25)
bias = np.ones((len(a2), 1))
a2 = np.hstack((bias, a2)) # size is (5000, 26)
z3 = np.dot(a2, self.theta2.T) # size is (5000, 10)
a3 = sigmoid(z3) # size is (5000, 10)
return a1, z2, a2, z3, a3
然后就是损失函数的处理。
损失函数先对原标签进行独热编码的处理,操作很简单,如下所示:
labels先设置成一个全0矩阵,应该是5000行,10列。然后根据原标签作为某一行的下标,相应位置置为1。
大家也可以上网查查好像有一个库函数直接可以进行OneHotEncoding,我忘了。
def onehotEncoding(self):
labels = np.zeros((len(self.X), self.num_labels)) # size is (5000, 10)
for i in range(self.num_labels):
for j in range(len(self.labels)):
if self.labels[j] == i:
labels[j, i] = 1
self.labels = labels
我们的损失函数就需要一个循环,以类别数为循环次数,每一次就对一个类别进行交叉熵函数的计算。
可以看到我在交叉熵损失函数后面写了一行验证初始损失的代码。
然后就是我们的正则项损失。我们的Theta1的size是(25, 401),因为我们的第一列是用于给偏置项的权值的,所以我们在做平方时列是从下标为1进行选取的。
np.power是element-wise的,也就是平方完仍旧是一个矩阵,所以我们要用一个sum将其拉回到一个数值,最后要乘上学习率lr。
def nnCostfunction(self, params, lr):
self.reshapeparams(params)
a1, z2, a2, z3, a3 = self.forwardPropagation()
# one-hot encoding! if label is 9, then transform it into [0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
# self.onehotEncoding(a3)
# labels = self.labels
# then apply cost function to it
cost = 0
for i in range(self.num_labels):
cost += -np.mean(self.labels[:, i] * np.log(a3[:, i]) + (1 - self.labels[:, i]) * np.log(1 - a3[:, i]))
# print("cost is %f" % cost) # the initial cost is 0.287629, it's verified!
# then we need to append the regularized cost
reg_cost = (np.sum(np.power(self.theta1[:, 1:], 2)) + np.sum(np.power(self.theta2[:, 1:], 2))) * lr
cost += (reg_cost / (2 * self.length))
# print("the cost is %f" % cost) # the initial cost(contains reg_cost) is 0.383770, it's verified!
return cost
params解释:
是这样的,我们在用高级的优化函数时,我们会把拟合系数theta用一个向量进行传入。所以我们的params实际上就是Theta1和Theta2两个矩阵展平后进行一个连接,变成一个向量。然后我们的优化函数根据导数优化params,但我们仍旧需要将params变换为Theta1和Theta2两个矩阵才能做矩阵运算!
所以这里特地写一个reshapeparams函数用于将当前的params转换为两个theta矩阵。因为我们一开始已经率先导入了weights,已经提前知道Theta1和Theta2的shape了,所以这里可以直接调用。
所以顺序一定要搞清楚!
def reshapeparams(self, params):
self.params = params
theta1 = self.params[:self.theta1.shape[0] * self.theta1.shape[1]]
theta2 = self.params[self.theta1.shape[0] * self.theta1.shape[1]:]
self.theta1 = theta1.reshape(self.theta1.shape)
self.theta2 = theta2.reshape(self.theta2.shape)
4.随机生成系数
前面的损失函数损失值验证完毕后我们需要自己随机生成初始拟合系数,如下所示:
在神经网络中我们不能简单地将所有权值置位0或者1等,所以会导致训练结果不理想,具体地可以直接去看视频。
def randomInitializeweights(self):
epsilon = 0.12
units_num = self.theta1.shape[0] * self.theta1.shape[1] + self.theta2.shape[0] * self.theta2.shape[1]
self.params = np.random.rand(units_num) * 2 * epsilon - epsilon
theta1 = self.params[:self.theta1.shape[0] * self.theta1.shape[1]]
theta2 = self.params[self.theta1.shape[0] * self.theta1.shape[1]:]
self.theta1 = theta1.reshape(self.theta1.shape)
self.theta2 = theta2.reshape(self.theta2.shape)
# this is what we really need to implement, the weights we read in load xxxx function is just to help
# you know whether your cost function has bugs
return self.params
5.反向传播
第一个iters是拿来等会展示训练进度的。
delta3是比较好解释,就是我们的输出层,我们在前面推导过了输出层的delta就是神经网络的输出与实际标签的差值。这里的减法也是element-wise的。
我们的循环就是每次处理一个数据也就是一张图片。最后会对每一个导数进行取均值。
我们的delta计算公式其实刚刚推导过但还是再看一眼吧:
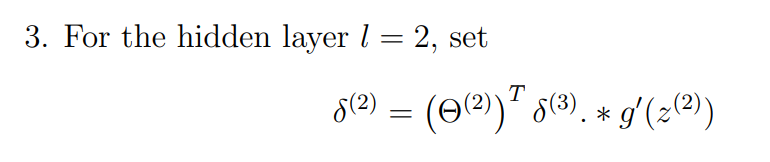
这个公式是对我们上面推导的东西做了向量化处理的。
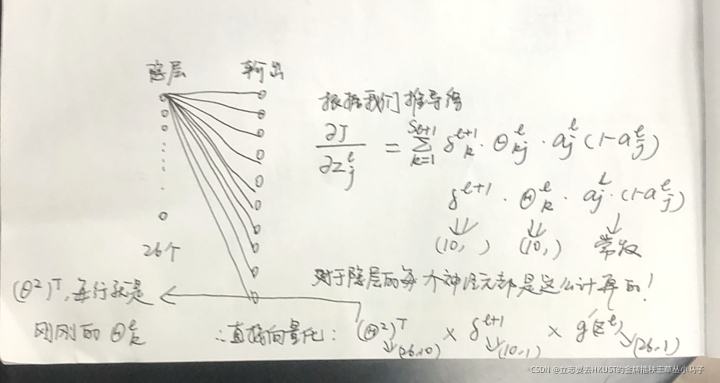
前两个用矩阵乘法,随后两个都是(26, 1)用element-wise的乘法。
所以可以观察下面的代码的d2t就是做的我们上面讲的这个。
直接对theta本身求导的就是我们的theta1和theta2了,也是采取了向量化的。
而且比较简单,就是用中间件d和a做矩阵运算即可。
反正最好能把向量化后的代码仔细推敲一下看看究竟做了啥是最好的!
def backPropagation(self, params, lr):
self.iters += 1
print("process ---%f%%" % ((self.iters / 250) * 100))
self.reshapeparams(params)
a1, z2, a2, z3, a3 = self.forwardPropagation()
# as we all know, δ is a index which measures the diff of θ
delta1 = np.zeros(self.theta1.shape)
delta2 = np.zeros(self.theta2.shape)
delta3 = a3 - self.labels # size is (5000, 10) each time we fetch a row whose size is (1, 10)
# temp = delta3[0, :].reshape(-1, 1) # shape is (10, 1)
for i in range(self.length): # here the loop means every time we just take one image(example) into account
a1t = a1[i, :].reshape(1, -1) # size is (1, 401)
z2t = z2[i, :].reshape(1, -1) # size is (1, 25)
a2t = a2[i, :].reshape(1, -1) # size is (1, 26)
# size of delta3[i, :] is (10,)
d2t = np.dot(self.theta2.T, delta3[i, :].reshape(-1, 1)) # size is (26, 1)
z2t = np.insert(z2t, 0, values=np.ones(1))
d2t = np.multiply(d2t.T, sigmoid_gradient(z2t)) # size is (1, 26)
delta2 += np.dot(delta3[i, :].reshape(-1, 1), a2t) # size is (10, 26)
delta1 += np.dot(d2t[:, 1:].T, a1t) # size is (25, 401)
# delta3 +=
delta2 /= self.length
delta1 /= self.length
# add the gradient regularization term
delta1[:, 1:] = delta1[:, 1:] + (self.theta1[:, 1:] * lr) / self.length
delta2[:, 1:] = delta2[:, 1:] + (self.theta2[:, 1:] * lr) / self.length
# unravel the gradient matrices into a single array
grad = np.concatenate((np.ravel(delta1), np.ravel(delta2)))
return grad
6.用库函数进行优化梯度下降过程,和之前的都一样,用scipy optimize的minimize函数传入关键的损失函数及梯度求导函数和待优化的系数。
因为训练神经网络尤其是大型的深度学习的网络都是一个复杂漫长的过程,训练完的结果我用pickle库函数进行打包存储以免一次次重复训练!
def fminc(self, params, lr, fp):
fmin = opt.minimize(fun=self.nnCostfunction, args=lr, x0=params, jac=self.backPropagation, method='TNC',
options={'maxiter': 250})
print(fmin)
with open(fp, 'wb') as fw:
pickle.dump(fmin, fw)
self.showHiddenlayers(fmin.x)
self.predict(fmin.x)
7.预测结果。
和ch03是一模一样的,只不过这次的参数是我们自己训练出来的:
def predict(self, params):
self.reshapeparams(params)
bias = np.ones((self.length, 1))
x = np.hstack((bias, self.X))
temp1 = sigmoid(np.dot(x, self.theta1.T))
temp1 = np.hstack((bias, temp1))
answers = sigmoid(np.dot(temp1, self.theta2.T))
results = np.argmax(answers, axis=1)
print("accuracy is %f" % (np.sum(results == self.Y) / self.length))
# al last, we can visualize the result~
# at last, we can just visualize the prediction
show_index = np.random.randint(0, self.length, 9)
for i in range(9):
plt.subplot(3, 3, i + 1)
plt.axis(False)
plt.imshow(np.transpose(self.X[show_index[i], :].reshape(20, 20)))
# because when we read file, real label subtracts 1, thus, we add 1 to corresponds to the image
# don't forget that the label of 0 is 10!!!
# by the way, we can learn the ternary operator in Python, it's just a little bit different than C++ or C
l1 = self.Y[show_index[i]] + 1 if self.Y[show_index[i]] + 1 < 10 else 0
l2 = results[show_index[i]] + 1 if results[show_index[i]] + 1 < 10 else 0
plt.title("label:%d pred:%d" % (l1, l2))
plt.show()
8.一些不是特别重要的小练习。
梯度检查,就是用极限法来求某个点的梯度
[J(θ+epsilon) - J(θ-epsilon) ]/2epsilon近似某一点的梯度。
我因为整个网络设置的不像吴老师给的那么完美所以没法用一个小网络来测试梯度,因此,整个检查过程十分缓慢我已经注释掉了,但结果还是有的!
设置选项最大训练轮次(我们已经在代码中展示了怎么设置,通过options用词典的方式设置)。
9.结果展示
准确率惊人,prodigious!
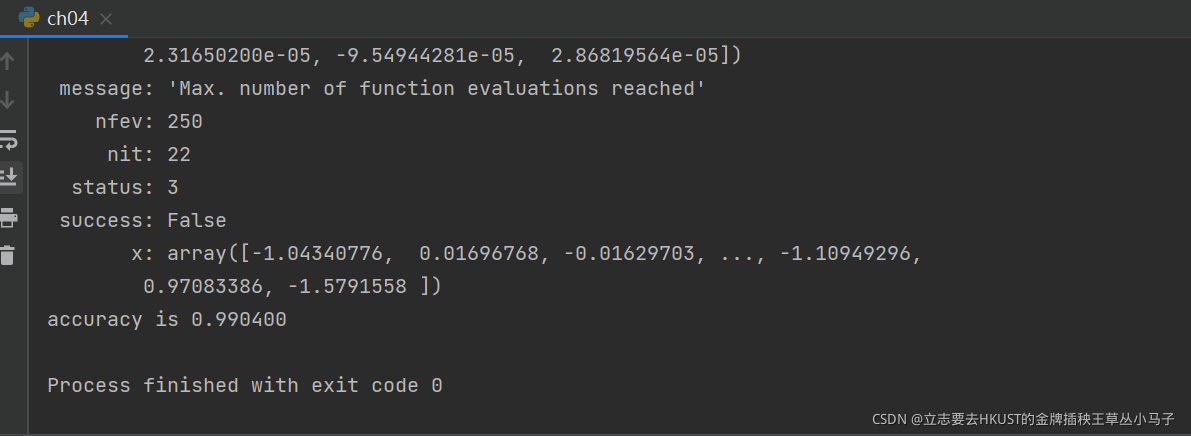
预测结果:
