核心思想
??本文提出一种将多种特征描述算法融合起来实现更好图像匹配的方法。近些年来,图像特征的描述算法层出不穷如SIFT、LIOP 、DAISY等等,每种方法都有各自的优势和侧重点,对于不同图像其效果也各有优劣。那么能不能将多种算法的优势结合起来,提出一种混合的特征描述算法来满足各个情况呢?最简单方法就是将多个特征向量级联或者加权求和得到融合特征向量,但这个方法有很大的问题,因为不同算法得到的特征向量维度不同,数值表达的含义也不同,因此简单的级联或者相加都不能保留原有算法的性能。如果要将多种特征描述算法更好的融合起来,就必须把他们映射到一个统一的空间中,在这个空间中各个算法的优劣有一个统一的度量方法。

??作者首先使用三种特征描述算法对两幅图像进行匹配,结果如上图(c)、(d)、(e)所示,黑色连线表示错误匹配,彩色连线表示正确匹配,作者发现无论是哪种特征描述算法,其正确匹配通常都满足几何连续性,他们的几何变换(单应性)都是一致的。这启发了作者将特征向量映射到单应性空间中,如图(f)所示,作者发现对于正确的匹配点,无论用任何特征描述算法,在该空间中的位置都是临近甚至是一致的,而误匹配点不同算法得到的映射坐标是不同的,无规律的散布在空间中。利用这一规律,作者利用一种无监督的单类SVM算法将正确匹配点分类出来。
实现过程
??根据上面的思路,作者首先使用Hessian-Affine检测器从两幅图像
I
P
I^P
IP和
I
Q
I^Q
IQ中分别提取关键点,构成点集
U
P
U^P
UP和
U
Q
U^Q
UQ,特征点的坐标表示为
x
i
\mathbf{x}_i
xi?,然后用
M
M
M种特征描述算法分别提取特征描述向量
{
f
i
,
m
}
m
=
1
M
\{f_{i,m}\}^M_{m=1}
{fi,m?}m=1M?。
C
~
=
U
P
×
U
Q
\tilde{C}=U^P\times U^Q
C~=UP×UQ表示所有特征点之间的对应关系,为了提高计算效率,对于每个
I
P
I^P
IP图中的特征点
u
P
u^P
uP都只保留相似程度最大的
r
r
r个匹配点作为后续匹配的候选对象,因此对于每个特征点、每种特征描述算法都会得到一个候选匹配点集
C
i
,
m
=
{
(
u
i
P
,
u
i
k
,
m
Q
∈
I
Q
)
}
k
=
1
r
C_{i,m}=\{(u_i^P,u_{i_k,m}^Q\in I^Q)\}_{k=1}^r
Ci,m?={(uiP?,uik?,mQ?∈IQ)}k=1r?,则每个特征点都有
r
×
M
r\times M
r×M个候选匹配点,而整个点集
U
P
U^P
UP中包含
N
P
N^P
NP个特征点,则整个匹配点集
C
C
C表示为

??对于特征点
u
i
u_i
ui?所在的特征描述区域(特征描述算法通常提取以特征点为中心的一块区域内的特征信息),经过仿射变换可得
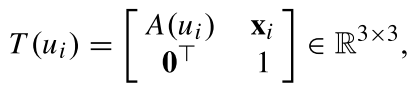
其中
A
(
u
i
)
A(u_i)
A(ui?)是一个
2
×
2
2\times 2
2×2的非奇异矩阵,用于记录特征点
u
i
u_i
ui?的尺度、形状和方向,对于
U
P
U^P
UP和
U
D
U^D
UD中的特征点都进行仿射变换,并得到下式
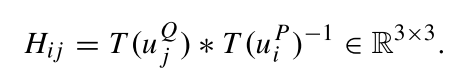
H
i
j
H_{ij}
Hij?是一个6自由度的仿射变换,他也可以看成是6维的仿射单应性空间
H
\mathcal{H}
H中的一个点。因此对于匹配点集
C
C
C中的任意一对匹配点
c
=
(
u
i
P
,
u
j
Q
)
c=(u^P_i, u_j^Q)
c=(uiP?,ujQ?)都可以映射到上述空间中的一个点。可考虑两对匹配点
c
=
(
u
i
P
,
u
j
Q
)
c=(u^P_i, u_j^Q)
c=(uiP?,ujQ?)和
c
′
=
(
u
i
′
P
,
u
j
′
Q
)
c'=(u^P_{i'}, u_{j'}^Q)
c′=(ui′P?,uj′Q?),其对应的放射单应性矩阵分别为
H
i
j
H_{ij}
Hij?和
H
i
′
j
′
H_{i'j'}
Hi′j′?,则匹配点
c
=
(
u
i
P
,
u
j
Q
)
c=(u^P_i, u_j^Q)
c=(uiP?,ujQ?)与
H
i
′
j
′
H_{i'j'}
Hi′j′?之间的投影误差可表示为
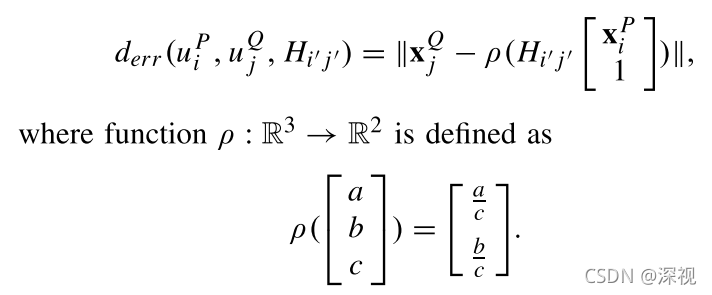
这个误差反映了将匹配点
c
=
(
u
i
P
,
u
j
Q
)
c=(u^P_i, u_j^Q)
c=(uiP?,ujQ?)的单应性矩阵从
H
i
j
H_{ij}
Hij?更换成
H
i
′
j
′
H_{i'j'}
Hi′j′?时产生的误差,进而两对匹配点之间的重投影误差可表示为
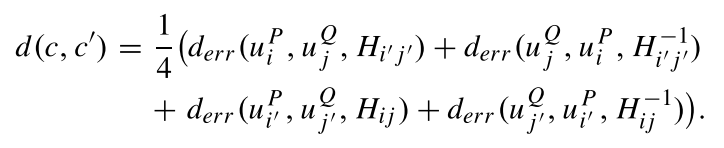
重投影误差用于计算两对匹配点之间的几何差异。
??作者构建了一个无向图
G
=
(
V
,
E
)
\mathcal{G}=(\mathcal{V},\mathcal{E})
G=(V,E)来描绘匹配点之间的几何和空间关系。图中的每个节点
v
i
v_i
vi?都对应一对匹配点
c
i
c_i
ci?,如果两个节点对应的匹配点
c
i
c_i
ci?和
c
j
c_j
cj?在图像
I
P
I^P
IP中的特征点
u
i
u_i
ui?和
u
j
u_j
uj?之间的距离足够近(这里距离足够近的概念是特征点
u
j
u_j
uj?是
u
i
u_i
ui?的K最近邻),则两个节点
v
i
v_i
vi?和
v
j
v_j
vj?之间有边
e
i
j
e_{ij}
eij?连接,且边上的权重如下
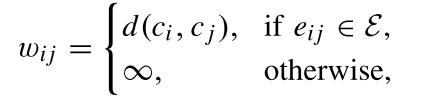
其中
d
(
c
i
,
c
j
)
d(c_i,c_j)
d(ci?,cj?)就是上文介绍的重投影误差,这表现了匹配点之间的几何一致性。为了描述匹配点在空间上的连续性,作者计算了
C
C
C中所有匹配点的测地距离
d
g
e
o
(
c
i
,
c
j
)
d_{geo}(c_i,c_j)
dgeo?(ci?,cj?),测地距离是指两个节点在图
G
\mathcal{G}
G中的最短路径距离。如前文所说,正确匹配点之间具备更强的几何和空间一致性,也即测地距离更短。
??最后作者使用一个单类SVM从匹配点集
C
C
C中选取出正确的匹配点,该方法假设正确的数据之间都是相似的,而错误数据之间各有各的不同。这一思想正好与正确匹配点之间具备更强的几何和空间一致性的思想不谋而合,因此可以用来识别正确的匹配点。SVM方法通过解决下述带约束的最优化问题来预测每个样本的标签,
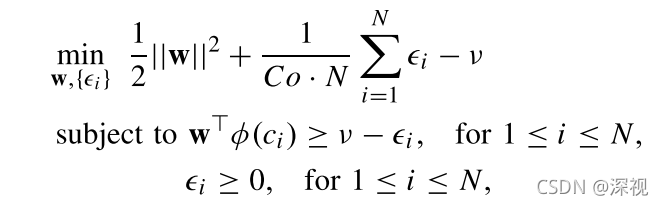
其中
C
0
C_0
C0?和
v
v
v是SVM的参数分别取1和0.5,函数
?
\phi
?将数据映射到再生核希尔伯特空间(RKHS),利用核技巧能够很容易的计算两个映射后数据之间的内积,即
k
(
c
i
,
c
j
)
=
<
?
(
c
i
)
,
?
(
c
j
)
>
k(c_i,c_j)=<\phi(c_i),\phi(c_j)>
k(ci?,cj?)=<?(ci?),?(cj?)>,本文选择的核函数为
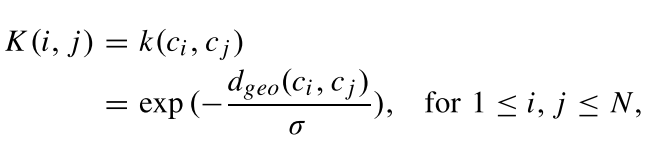
其中
σ
\sigma
σ设置为每对匹配点到其最近邻之间的平均测地距离。每对匹配点
c
i
c_i
ci?对应的匹配得分
f
(
c
i
)
f(c_i)
f(ci?)可得
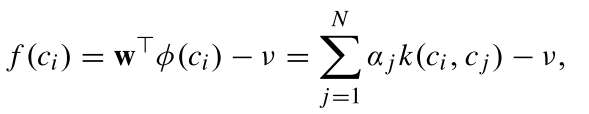
其中
α
j
\alpha_j
αj?表示支持向量的优化系数,对于每对匹配点对应的匹配点集
C
i
C_i
Ci?(其中包含多种特征描述算法对应的匹配结果),选择匹配得分最高的点作为最终的匹配点。
创新点
- 通过将匹配点映射到放射单应性空间中,使得多种特征描述算法具有统一的比较标准
- 设计重投影误差和测地距离来描述匹配点之间的几何一致性和空间连续性
- 利用单类SVM算法来预测每对匹配点使用不同特征描述算法的匹配得分,并选择得分最高的作为最终匹配点
算法评价
??本文是从特征描述算法的角度来提高匹配效果的,融合多种特征描述算法并从其中选择出对于当前匹配点最好的方法。通过仿射变换解决了不同的特征描述算法之间无法直接比较和融合的问题,并且利用正确匹配点具备较高的几何和空间连续性的这一假设,通过构建重投影误差和测地距离来计算匹配得分。这一思想还是很有特色,而且曾经也备受关注,但问题是计算耗时实在太长了,单幅图像匹配时间长达36秒,这对于很多应用而言是无法接受的。
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。