[人工智能]如何使用决策边界评估逻辑回归？

前言：本文主要为简单介绍决策边界，以及使用自定义函数绘制决策边界，不涉及决策边际的深度探讨。

内容分为两个模块：1. 介绍什么是决策边界；2. 如何通过自定义函数绘制逻辑回归的决策边界。

如何理解决策边界？

定义：在二维空间中，通过一条线将二分类的标签划分为两个部分，这条线称为决策边界。

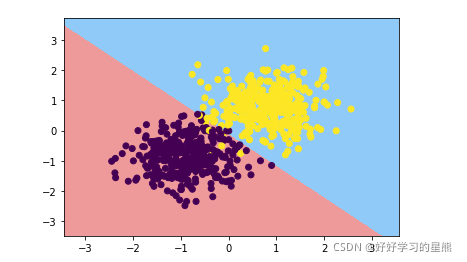
特点：

1. 不同的模型决策边界的形态不一样；比如KNN的决策边界可能是曲线；

2. 可以直观体现模型效果；比如是否过拟合，如果边界两侧融合的数据较多，那么模型可能存在过拟合；

3. 可视化只适用于2维/3维空间，更高维度的空间无法绘制。

如何绘制逻辑回归的决策边界？

自定义函数的思路、代码：

1. X的范围扩大1，打点；

2. 训练模型；

3. 将打点值放到训练好的模型上预测得到标签；

4. 绘制决策边界

# 自定义逻辑回归绘制决策边界的函数
def logit_DB(X,w,y):
    x1,x2=np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,1000)
                      ,np.linspace(X[:,1].min()-1,X[:,1].max()+1,1000)
                     )
    
    X_temp=np.concatenate([x1.reshape(-1,1)
                           ,x2.reshape(-1,1)
                           ,np.ones(shape=(1000000,1))],1)
    
    y_hat_temp=logit_cla(sigmoid(X_temp.dot(w)))
    y_hat=y_hat_temp.reshape(x1.shape)
    
    from matplotlib.colors import ListedColormap
    custom_cmap=ListedColormap(['#EF9A9A','#90CAF9'])
    plt.contourf(x1,x2,y_hat,cmap=custom_cmap)

如何绘制逻辑回归的决策边界（案例：逻辑回归模型_二分类数据集）

案例中涉及自定义函数为：arrayGenCla（生成数据集）、array_split（划分训练集和测试集）、z_score（标准化）、sgd_cal（小批量梯度下降）、logit_gd（逻辑回归的损失函数）、logit_acc（逻辑回归的准确率评估）

1. 创建数据集

# 创建数据集
seed=9
np.random.seed(seed)
f,l=arrayGenCla(num_class=2,deg_dispersion=[6,2],bias=True)
X_train,X_test,y_train,y_test=array_split(f,l,random_state=24)
X_train[:,:-1]=z_score(X_train[:,:-1])
X_test[:,:-1]=z_score(X_test[:,:-1])
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)
plt.show()

??

2. 训练模型并查看学习曲线

# 训练模型并查看学习曲线
np.random.seed(seed)
n=X_train.shape[1]
w=np.random.randn(n,1)

epoch=200
lr_lambda=lambda epoch:0.95**epoch
score_train=[]
score_test=[]

for i in range(epoch):
    w=sgd_cal(X_train,w,y_train,logit_gd,epoch=1,batch_size=50,lr=0.2*lr_lambda(i))
    score_train.append(logit_acc(X_train,w,y_train))
    score_test.append(logit_acc(X_test,w,y_test))
    
plt.plot(range(epoch),score_train,label='score_train')
plt.plot(range(epoch),score_test,label='score_test')
plt.legend()
plt.show()

??

3. 绘制训练集上的决策边界

# 绘制训练集上的决策边界
logit_DB(X_train, w, y_train)
plt.scatter(X_train[:,0],X_train[:,1],c=y_train)
# plt.scatter(X_test[:,0],X_test[:,1],c=y_test) # 查看决策边界在测试集上的效果
plt.show()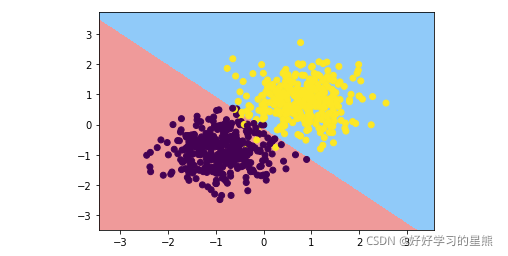

逻辑回归的参数大小是否代表特征重要性？（案例：逻辑回归的决策边界_鸢尾花数据集）

案例说明：此案例通过使用鸢尾花部分数据集，绘制逻辑回归模型的决策边界。将逻辑回归求得的特征参数与决策边界对比，用以说明决策边界对模型评估的应用场景。

案例中代码涉及使用部分自定义函数

# 创建数据集
data=pd.read_csv('iris.csv')

features_temp = np.copy(data.iloc[:, 1: 3].values)
labels_temp = np.copy(data.iloc[:, -1].values)

labels_temp[labels_temp!='Iris-setosa']=0
labels_temp[labels_temp=='Iris-setosa']=1

labels=labels_temp.astype(float).reshape(-1,1)
features=np.concatenate([features_temp,np.ones(shape=labels.shape)],1)

# 模型训练并绘制决策边界
seed=24
np.random.seed(seed)
n=features.shape[1]
m=np.random.randn(n,1)
epoch=200
lr_lambda=lambda epoch: 0.95**epoch

for i in range(epoch):
    w=sgd_cal(features,w,labels,logit_gd,epoch=1,batch_size=10,lr=0.5*lr_lambda(i))

print(w)
print(logit_acc(features,w,labels,thr=0.5))

logit_DB(features,w,labels)
plt.scatter(features[:,0],features[:,1],c=labels)
plt.show()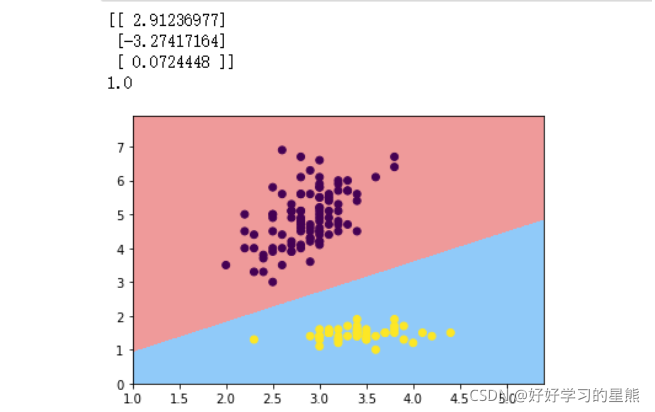

?

结论：不代表。因为w的随机性、实际数据集上可能存在局部最小值等原因，导致模型不一定迭代到全局最小值点；同时数据集分类差异较大，也存在多个决策边界可以划分数据集。

是否存在多个决策边界，则可以通过决策边界可视化查看。比如图中，两个分类的标签间距很大，这个间距中可以绘制任意多个决策边界。