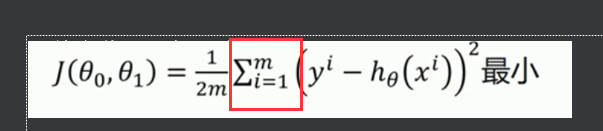[人工智能]人工智能入门

1 什么是人工智能

• Artificial Intelligence，亦称智械、机器智能，
• 指由人制造出来的机器所表现出来的智能
• AI的核心问题包括建构能够跟人类似甚至超卓的推理、知识、规划、学习、交流、感知、移物、使用工具和操控机械的能力等

2 人工智能的分类

• 弱人工智能 如除了语音识别，啥都不能干
• 强人工智能 如自动驾驶
• 超人工智能 全能，推理能力

3 人工智能研究分支

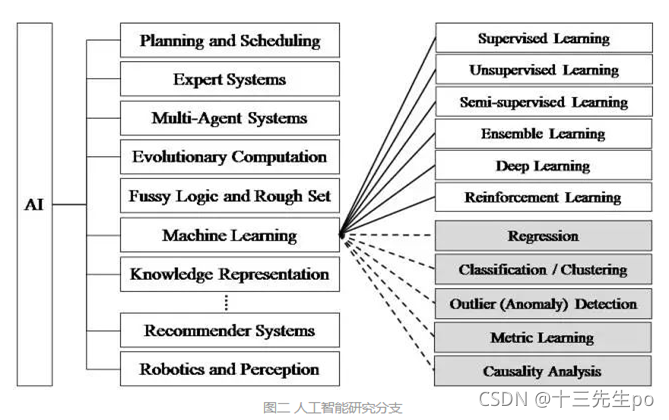
• 机器学习AI （Machine Learning AI）
  • 机器学习是要在大数据中寻找一些“模式”，然后在没有过多的人为解释的情况下，用这些模式来预测结果，而这些模式在普通的统计分析中是看不到的
    • 大量的数据
    • 发现规律
• 深度学习(Deep Learning)
  • 人工神经网络
  • 是机器学习中最热门的算法
    

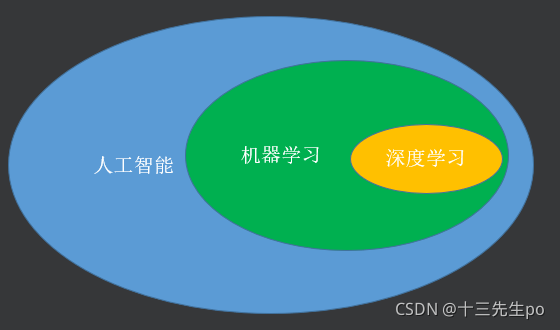
4 机器学习

• 人工智能的一个分支
  • 什么是学习？
    一个成语就可概括：举一反三，懂解题方法，因此考场上面对陌。高考为例，高考的题目在上考场前我们未必做过，但在高中三年我们做过很多很多题目生问题也可以算出答案
  • 推理机器学习在近30多为主线，从数据中自动分析获得规律
  • 近年已发展为一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、计算复杂性理论等多门学科
  • 设计和分析一些让计算机可以自动“学习”的算法

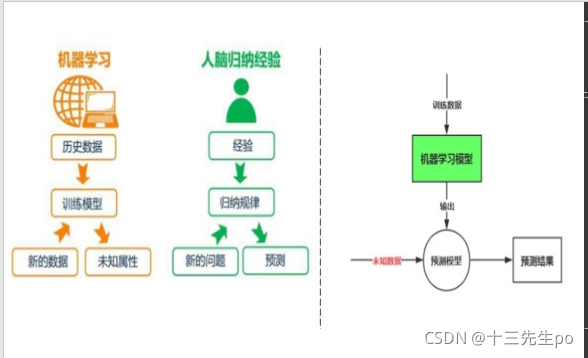
4.1 机器学习的核心任务

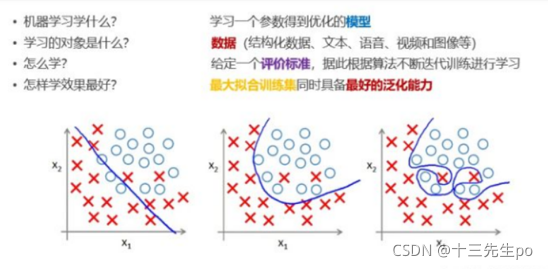
训练过度，虽然准确度很高，但是不符合实际应用，左边的训练成果已经很好了

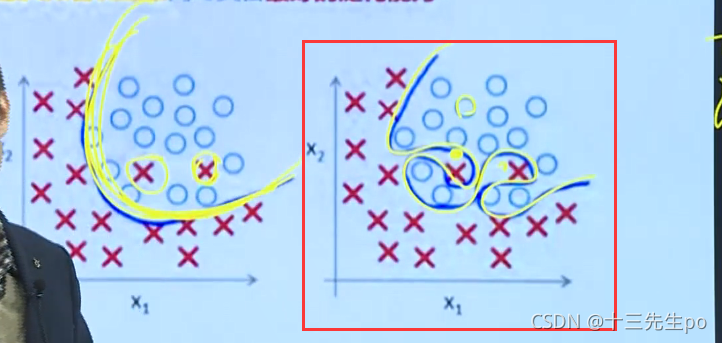
4.2 学好机器学习的第一原则和要义

4.3 机器学习分类

• 监督学习（有目标的，如年龄和肿瘤良性恶性是否有关系）
• 无监督学习
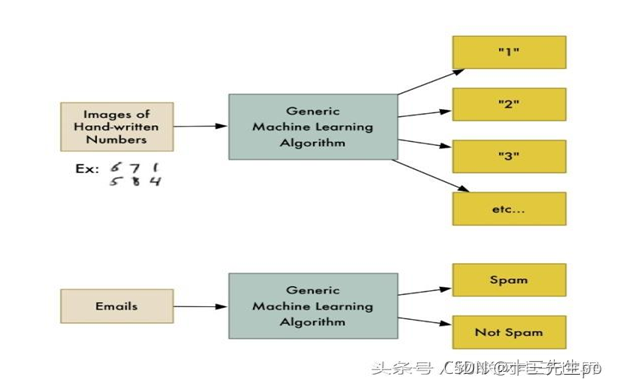
• 最简单也最普遍的一类机器学习算法就是分类（classification）。对于分类，输入的训练数据有特征（feature），有标签（label）。所谓的学习，其本质就是找到特征和标签间的关系（mapping）。这样当有特征而无标签的未知数据输入时，我们就可以通过已有的关系得到未知数据标签。
• 在上述的分类过程中，如果所有训练数据都有标签，则为有监督学习（supervised learning）。如果数据没有标签，显然就是**无监督学习（unsupervised learning）**了，也即聚类（clustering）。

监督学习



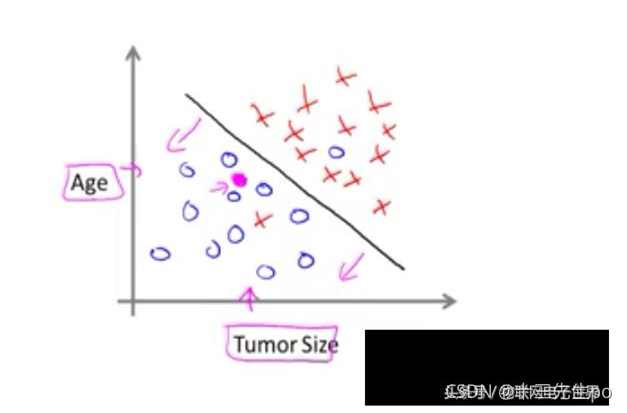
无监督学习

“自学成才”,没有老师的“指导”，没有明确的目的。要回答的问题是“从数据X中能发现什么”。
通过无监督学习，我们可以快速把行为进行分类，虽然我们不知道这些分类意味着什么，但是通过这种分类，可以快速排出正常的用户，更有针对性的对异常行为进行深入分析。

• 案例1：发现异常

  • 有很多违法行为都需要”洗钱”，这些洗钱行为跟普通用户的行为是不一样的，到底哪里不一样？
  • 如果通过人为去分析是一件成本很高很复杂的事情，我们可以通过这些行为的特征对用户进行分类，就更容易找到那些行为异常的用户，然后再深入分析他们的行为到底哪里不一样，是否属于违法洗钱的范畴。

• 案例2：用户细分

  • 这个对于广告平台很有意义，我们不仅把用户按照性别、年龄、地理位置等维度进行用户细分，还可以通过用户行为对用户进行分类。
  • 通过很多维度的用户细分，广告投放可以更有针对性，效果也会更好。

• 案例3：推荐系统

  • 大家都听过”啤酒+尿不湿”的故事，这个故事就是根据用户的购买行为来推荐相关的商品的一个例子。
  • 比如大家在淘宝、天猫、京东上逛的时候，总会根据你的浏览行为推荐一些相关的商品，有些商品就是无监督学习通过聚类来推荐出来的。系统会发现一些购买行为相似的用户，推荐这类用户最”喜欢”的商品。

5 学习人工智能步骤

• 基本数学知识
  • 微积分基础
  • 线性代数
  • 概率论
• 编程语言
• 机器学习算法
• 人工神经网络

6 一元线性回归

6.1 回归概念

• 高尔顿(达尔文表兄)提出
  • 研究父辈身高和字辈身高关系
    通过大量统计表明矮个子的父辈的子女平均身高高于父辈，高个子身高的父辈子女平均身高低于父辈。
  • 通俗的讲，姚明的孩子身高超过姚明的概率很低，潘长江的孩子超过潘长江的概率很高。
  • 大自然有种力量让物种趋于平均。这种现象就叫回归

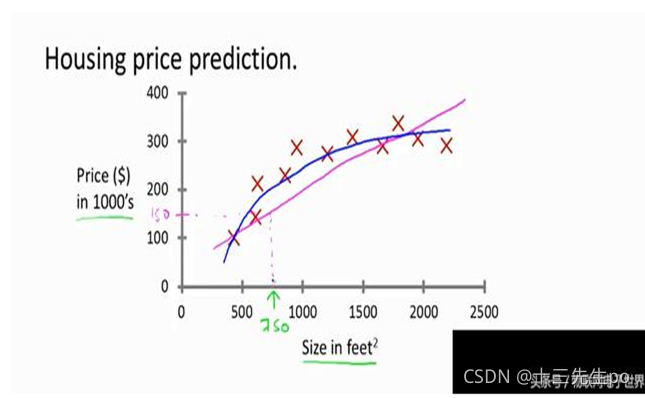
6.2 线性回归适用场景

• 身高体重预测
  
• 房价预测等
  

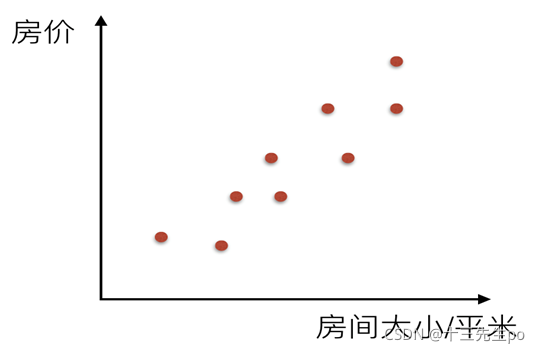
6.3 线性回归方程

• 一元线性回归
  f(x) = w1*x+w0
• 多元线性回归
  f(x1,x2…xn) = w0+w1X1+w2X2+…wn*Xn
  

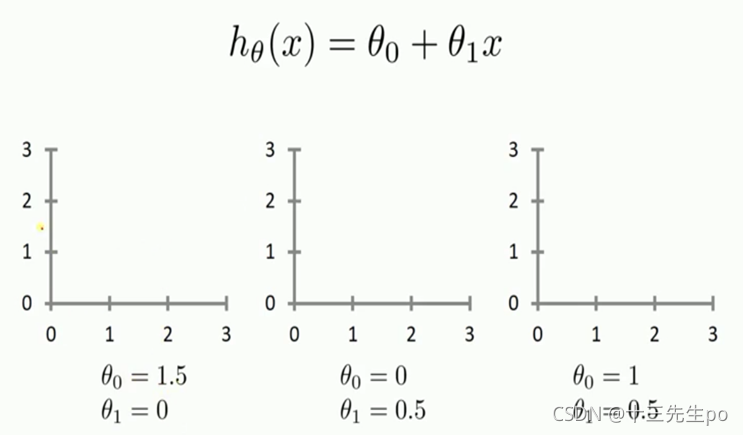
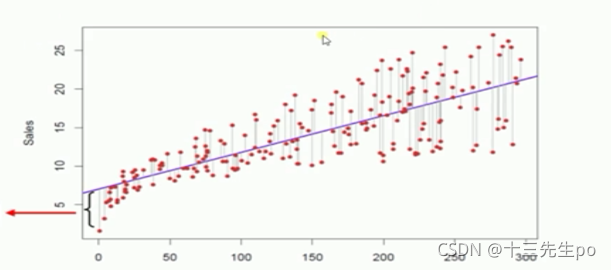
拟合直线的原则

• 最小二乘法
• 真实值和预测值的误差最小
• 每个点和直线的距离平方和最小。
  判断哪条直线最合适
  

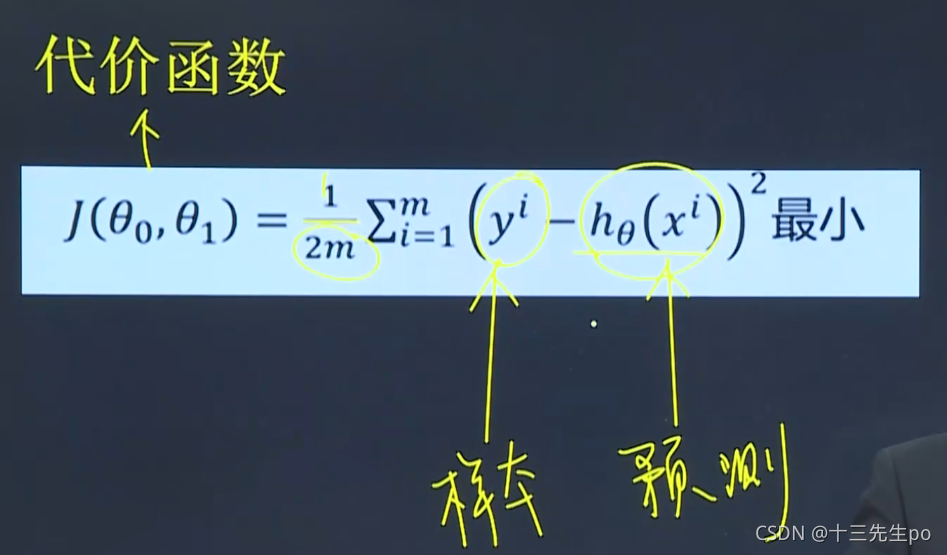
6.4 利用最小二乘法求解——代价函数

参考书籍

高数书第九章：

• 第八节 多元函数的极值及其求法
• 第十节 多元函数的极值及其求法

利用最小二乘法求解体现出来的公式如下：均方差最小，求平方和之后要除以m，平方求导有个2，加个1/2方便约掉（这里加个2只是为了方便计算，因为只是要求极值点，所以本身的值并不重要，乘以一个系数并不改变极值点的位置）

我们要求解的是：θ1是斜率，θ0是x等于0时的最大值

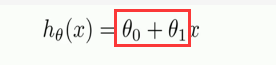
6.4.1 代价函数计算

数学必备知识：导数概念、复合函数求导法则、偏导数、极大值，极小值概念、梯度概念

• 最小二乘法
  
• 最小二乘法求解
  求极大值和极小值时，是求其导数=0的时候
  则求两个参数θ1、θ0的偏导数
  对θ0、θ1求偏导数得以下结果：θ1是斜率，θ0是x等于0时的最大值
  

大致化开的结果：

将1式和2式合并求解得：

求解过程比较麻烦，我们选用梯度下降法

6.5 梯度下降算法

选取一点，选择比较陡的方向走，走到准备开始向上为止

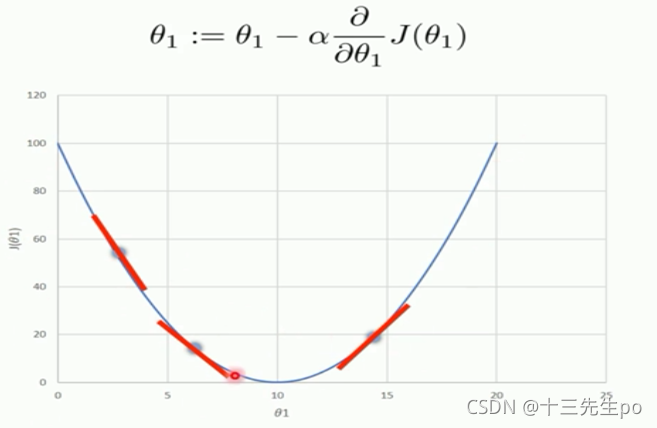
• 确定当前位置的损失函数的梯度，对于θi,其梯度表达式如下：（如果是一元线性，J里面只需要一个参数，即是“J（θ0）”）

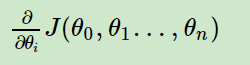
• 用步长乘以损失函数的梯度，得到当前位置下降的距离，即
  

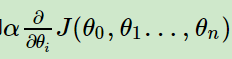
• 确定是否所有的θi,梯度下降的距离都小于ε，如果小于ε则算法终止，当前所有的θi(i=0,1,…n)即为最终结果

• 更新所有的θ，对于θi，其更新表达式如下。更新完毕后继续转入步骤1
  

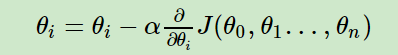
• 线性方程中，对θ1不断重新赋值，a是步长。迭代这个参数值

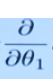
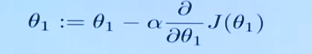
6.5.1 步长大小的影响

情况1：每次下降的步长过小，也能找到点，但是收敛的时间特别长

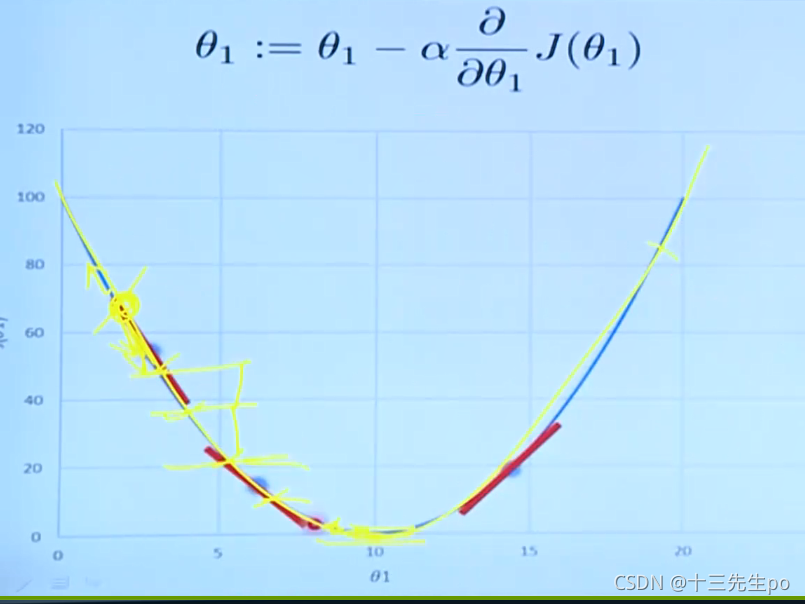
情况2：每次下降的步长过大，如果高了就往回走，出现振荡，找谷底比较难

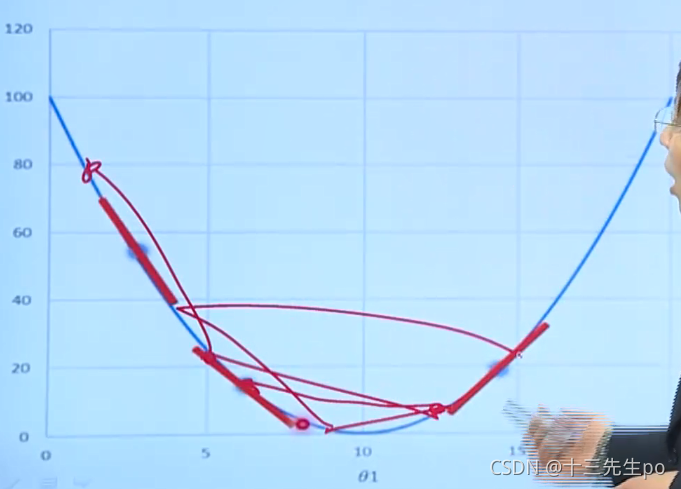
6.5.2 凸函数和非凸函数

非凸函数一般画不出来，影响的参数比较多，二维（只有一个自变量）可能画不出来，

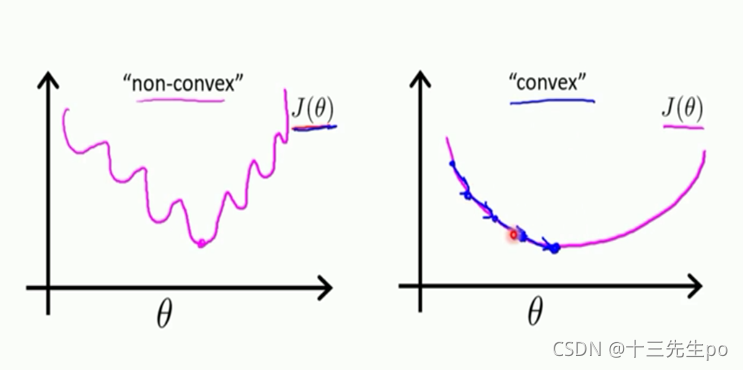
例如该三维图，有多个谷底，有多个参数

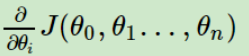
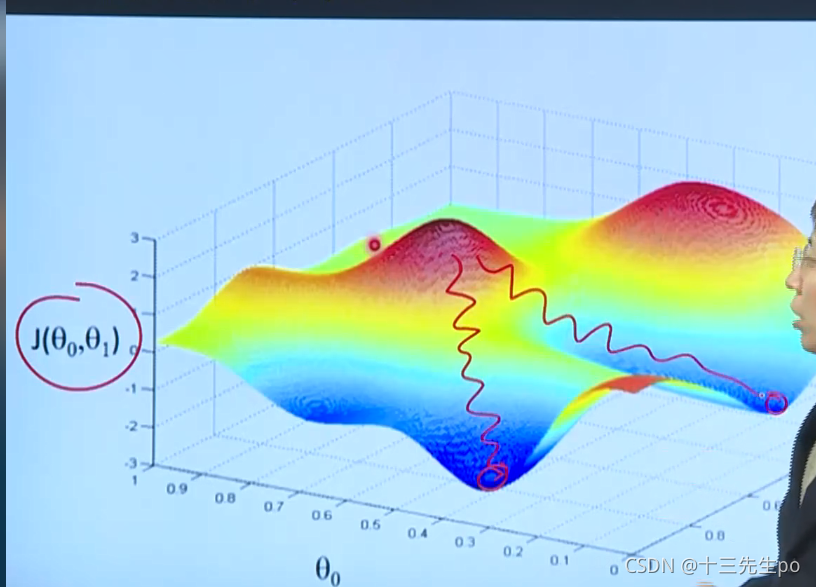
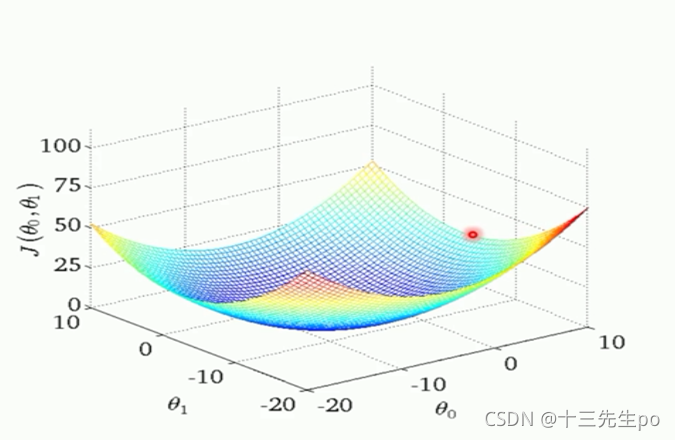
最理想的状况就是有一个“V”的极值

6.5.3 单变量函数的梯度下降

• 梯度下降的计算公式
  
  
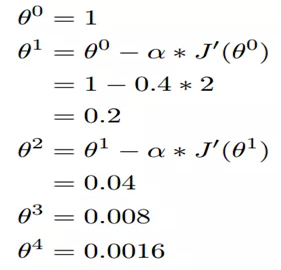
  慢慢接近终点
  
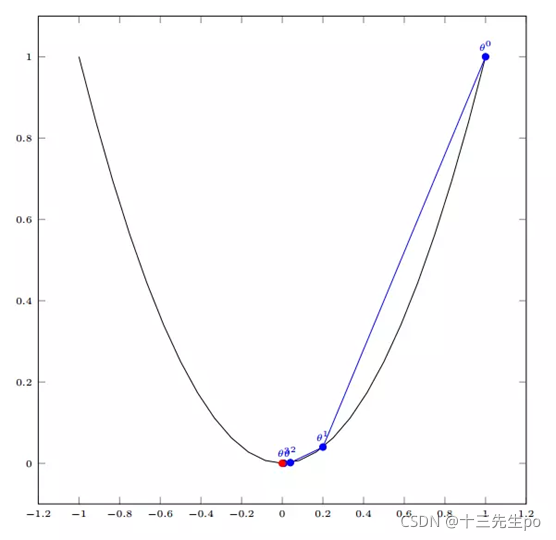
• 一元函数的梯度下降算法
  • 将前面计算好的求导结果拿过来使用
    
    得到以下结果
    

6.5.4 一元线性回归实战1(房价预测)

m是迭代的次数
代价函数是利用每个x,y值求出对应的数值得到的结果的求和