1,
supervise监督学习与强化学习的区别在于:监督学习需要根据棋盘信息而告诉机器下一步动作,而强化学习,只需要让机器自己进行游戏.得到reward,然后评估每一步.


2,回归

x的下标用来表示x的某一特征
x的上标用来表示某个x样本

在第一步找到很多函数,然后在第二部由损失函数找到最好的那个函数.损失函数有多种.

该图为损失函数对每个w,b画的图形,颜色表示损失值.越偏蓝色代表越好.
找到最好方程时:可以用正规方程,也可以用梯度下降.


gradient表示这一部分
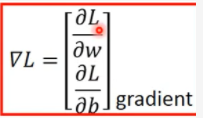

w,b向等高线法线方向移动.
在线性回归中,损失函数定义为均方误差的形式,那么不需要担心找到极小点,而不是最小点,因为它的损失函数如上图,是光滑均匀的只有一个最小点.


注意这里error与均方误差的损失函数很像.
如何做到更好,



模型复杂可能会造成过拟合问题.Overfitting

由此可以看出,只考虑cp值,作为特征是不正确的.


引入冲激函数的概念.



对损失函数进行正则化,解决过拟合问题.如上图:希望w越小越好,因为w越小,拟合出的曲线越平滑,受输出影响越小.即不会引起突变.
平滑程度与b无关,所以不考虑b,b表示上下移动.

取样N次,每一次算出的平均值都不一定等于真实的平均值,但是平均值的期望值一定是等于真实的平均值的,期望值就是各概率乘以结果的总和.这样期望值等于真实的平均值的就是无偏估计.这里的平均值与方差指的是,最好函数的平均值与方差,而不是我们采样出来的.

虽然是无偏估计,但是由于方差关系,还是不能得到真实平均值.N取越大,即每个样本中数据越多,越接近.

评估方差Variance,他是有偏的,因为他的期望值不等于真正的方差.即做很多次实验,也得不到真正的方差.

每次数据的误差来源于两部分.bias与variance,bias表示瞄准的点,variance表示实际打出比瞄准点偏移多少.variance小,表示实验数据集中,bias小表示多次实验数据的平均值接近红心.

模型简单,多次取样后得到的结果,有低方差.

理论上如果是无偏估计那么,进行无穷次实验,对所有实验找到的f取平均,就是最好的,真实的f.

如上图.蓝色的线与黑色的线之间的差距就可以理解为bias

所以简单模型代表低方差高bias.

模型越复杂,bias误差越小,但variance误差越大,所以总误差蓝色的线呈现上图形状.并且如果误差主要来自于bias误差就是欠拟合,来自于variance就是过拟合.


但是正则化可能会提高bias误差.

所以说public的结果并不可靠

使用n折交叉验证方法来尽量消除影响.