[人工智能]《蜥蜴书》_讲义及源码解读_11

训练神经网络

梯度消失/爆炸问题

反向传播算法的工作原理：是从输出层（高层）到输入层（低层），传播误差的梯度。 一旦算法计算出网络中每个参数的损失函数的梯度，就可以使用梯度下降来更新每个参数。

梯度消失：随着方向传播算法进展到较低层，梯度往往变得越来越小。 梯度下降更新使得较低层的连接权重实际上保持不变，并且训练永远不会收敛到最优解。 这被称为梯度消失问题。

梯度爆炸：在另一些情况下，正好相反：梯度可能变得越来越大，许多层得到了非常大的权重更新，算法发散。这是梯度爆炸的问题，在循环神经网络中最为常见。

原因的分析和猜测

著名的饱和激活函数Sigmoid ：$\sigma (x)=\frac{1}{1+e^{?x}}$

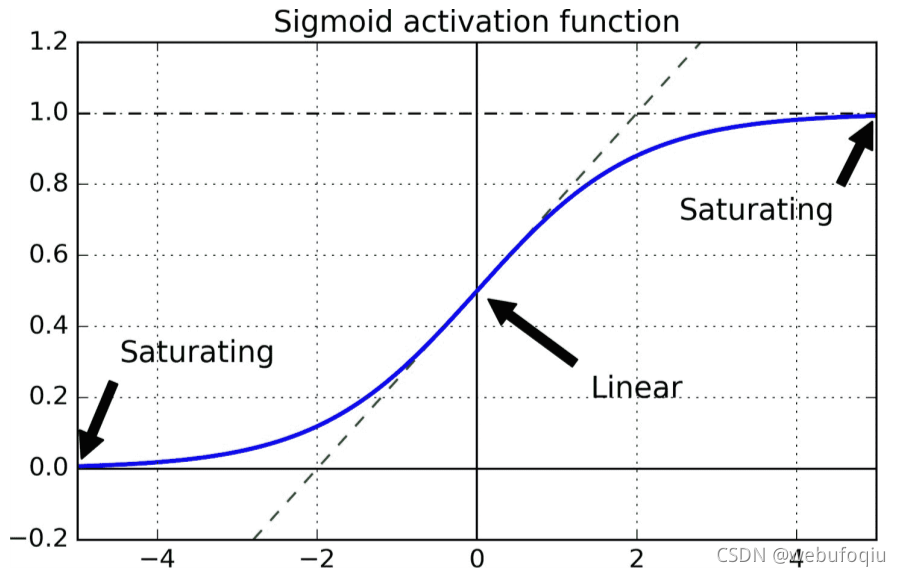
流行方案：sigmoid 激活函数和标准正态分布的权重参数初始化方法的组合。

每层输出的方差远大于其输入的方差。随着网络前向传播，每层的方差持续增加，直到激活函数在顶层饱和。

sigmoid函数的平均值为 0.5，导函数的值在0到0.25之间。如图，当输入变大（负或正）时，函数饱和在 0 或 1，导数非常接近 0。因此，当反向传播开始时， 它几乎没有梯度通过网络传播回来，而且由于反向传播通过顶层向下传递，所以存在的小梯度不断地被稀释，因此较低层得到的改善很小。

著名的饱和激活函数tanh: $tanh(x)=\frac{e^x?e^{?x}}{e^x{+}^{?x}}$

双曲正切函数的函数值在 -1到+1之间，函数平均值为0，其导函数值在 0到1之间（也是小于1的），同样不能避免梯度消失问题

（因其平均值为0，双曲正切函数在深度神经网络中的表现优于sigmoid 函数）

显著缓解这个问题的方法

进行预测时是前向的，在反向传播梯度时是逆向的。 不希望信号消失，也不希望它爆炸并饱和。

复习下正态分布（高斯分布）概率密度函数：
$$\begin{gathered} f(x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{?\frac{(x?\mu {)}^2}{2{\sigma }^2}} \\ 其中：{\sigma }^2方差为1，\mu :期望为0时，称之标准正态分布。 \end{gathered}$$

使用新的初始化策略（Glorot 初始化）

$$\begin{gathered} 正态分布，期望为0，方差为：{\sigma }^2=\frac{1}{fa{n}_{avg}} \\ 或者： \\ ?r和+r之间的均匀分布：其中:r=\sqrt{\frac{3}{fa{n}_{avg}}} \\ fa{n}_{in}:扇入，某层输入数量 \\ fa{n}_{out}:扇出，某层输出数量，即神经元数量 \\ fa{n}_{avg}=(fa{n}_{in}+fa{n}_{out})/2 \end{gathered}$$
研究者们经历了十多年才意识到初始化策略的重要性。使用 Glorot初始化可以大大加快训练，这是促成深度学习成功的技术之一。

LeCun初始化策略：

将上面公式中的 $fa{n}_{avg}$ 替换为 $fa{n}_{in}$ 即为 LeCun初始化策略（大名鼎鼎的杨立昆），

He 初始化策略

令公式中 ${\sigma }^2=\frac{2}{fa{n}_{in}}$

如下表：（都使用正态分布，而非均匀分布的情形）

如上表，默认情况下，Keras使用均匀分布的 Glorot初始化函数，即kernel_initializer='GlorotUniform' ，激活函数是sigmoid。

查看keras 中kernel_initializer的所有选项

[name for name in dir(keras.initializers) if not name.startswith("_")]

将设置 kernel_initializer="he_normal"

keras.layers.Dense(10, activation="relu", kernel_initializer="he_normal")  #激活函数使用RELU

著名的非饱和激活函数

RELU激活函数： $f(x)=max(0,x)$

在深度神经网络中表现很好，凭借其线性、非饱和的形式，克服梯度消失的问题，加快训练速度。

但不完美，它不是以0 位中心的函数，且当输入负数时，则完全不激活，ReLU函数死掉。

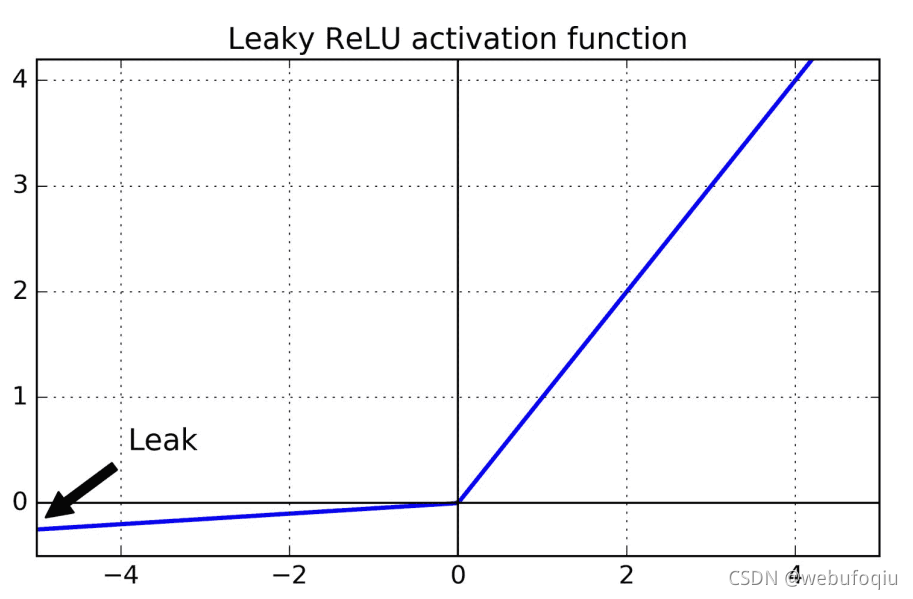
leaky ReLU激活函数：

$f(x)=max(\alpha x,x)\alpha 是超参数，含义是x<0时一个很小的斜率，默认0.01$

PReLU激活函数：

$f(x)=max(\alpha x,x)\alpha 不是超参数，可以在训练期间学习$

ELU激活函数：

$$f(x)=\{\begin{array}{ll}\alpha (e^x?1),& x\le 0\\ x& x>0\end{array}$$
ELU的表现优于所有 ReLU 变体：训练时间减少，神经网络在测试集上表现的更好。主要缺点是计算速度慢于 ReLU 及其变体（由于使用指数函数），但是在训练过程中，理论上是可以通过更快的收敛速度来补偿的。

SELU激活函数：

$$f(x)=\lambda \{\begin{array}{ll}\alpha (e^x?1)& x\le 0\\ x& x>0\end{array}$$

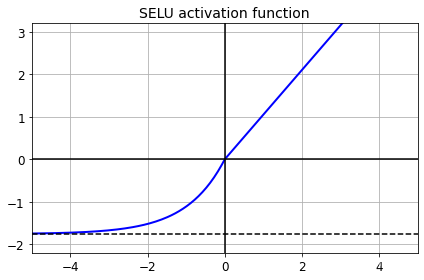
SELU 的效果常常优于其他激活函数。但有前提条件(自归一)：

• 输入特征必须是标准化的（平均值是 0，标准差是 1）

• 每个隐藏层的权重必须是 LeCun正态初始化的。即Keras 中，要设置kernel_initializer="lecun_normal"

• 网络架构必须是顺序的，也就是说其在循环神经网络或具有跳过连接的网络中，SELU 表现不佳；

• 所有层都是紧密层才保证自归一。(但有些研究者发现 SELU激活函数也可以提高卷积神经网络的性能)

• SELU 示例代码：

• alpha_0_1 = -np.sqrt(2 / np.pi) / (erfc(1/np.sqrt(2)) * np.exp(1/2) - 1)
  scale_0_1 = (1 - erfc(1 / np.sqrt(2)) * np.sqrt(np.e)) * np.sqrt(2 * np.pi) *
  (2 * erfc(np.sqrt(2))*np.e**2 + np.pi*erfc(1/np.sqrt(2))**2*np.e - 2*(2+np.pi)*erfc(1/np.sqrt(2))*np.sqrt(np.e)+np.pi+2)**(-1/2)
  # 互补误差函数，efrc, 对输入进行特征处理
  
  def elu(z, alpha=1):   
      return np.where(z < 0, alpha * (np.exp(z) - 1), z)
  def selu(z, scale=scale_0_1, alpha=alpha_0_1):
      return scale * elu(z, alpha)
  
  z = np.linspace(-5, 5, 200)  #-5到5均匀的200个点
  plt.plot(z, selu(z), "b-", linewidth=2) # 蓝线  selu
  plt.plot([-5, 5], [0, 0], 'k-')  # X轴
  plt.plot([-5, 5], [-1.758, -1.758], 'k--')  #渐近线
  plt.plot([0, 0], [-2.2, 3.2], 'k-')  # Y轴
  plt.grid(True)
  plt.title("SELU activation function", fontsize=14)
  plt.axis([-5, 5, -2.2, 3.2])
  plt.show()
      
  

如何选择激活函数

• 通常的顺序：SELU -> ELU -> leaky ReLU -> ReLU -> tanh -> sigmoid(logistic)
• 如果网络架构不能自归一化，选ELU 优于 SELU
• 如果把速度放首位，RELU 是最佳选择
• 如果出现过拟合或训练集太大，则选择PReLU
• 如果有空闲时间或算力，可以通过交叉验证来评估每个激活函数

批量归一化（Batch Normalization）

2015年，Sergey Ioffe 和 Christian Szegedy 提出了一种称为批量归一化（BN）的方法来解决梯度消失/爆炸问题。公式如下：
$$\begin{gathered} {\mu }_B=\frac{1}{m_B}\sum _{i=1}^{m_B}{x}^{(i)} \\ {x}^{(i)}:是实例i \\ {m}_B:是小批量中的实例数量 \\ {\mu }_B:是用整个小批量B的实例估算出的均值向量 \\ {\sigma }_B^2=\frac{1}{m_B}\sum _{i=1}^{m_B}(x^{(i)}?{\mu }_B{)}^2 \\ {\sigma }_B^2:用整个小批量估算出的方差向量（\sigma 标准差） \\ {\hat{x}}^{(i)}=\frac{x^{(i)}?{\mu }_B}{\sqrt{{\sigma }_B^2}+?} \\ {\hat{x}}^{(i)}:零中心和标准化后的实例i的输入矢量 \\ {z}^{(i)}=\gamma x^{(i)}+\beta 此处非点乘，是对应元素相乘 \\ \gamma :是缩放参数向量，每个输入对应一个缩放参数 \\ \beta :是偏移参数向量，每个输入对应一个偏移参数 \\ {z}^{(i)}:是批归一化的输出，即BN层的输出 \end{gathered}$$
思路：

• 该算法（或者说批归一化层）放在每个隐藏层的激活函数之前或之后；
• 具体操作就是将输入零中心并归一化（均值为 0，方差为 1）得到 ${\hat{x}}^{(i)}$，然后用两个新参数：$\gamma$ 参数用于缩放，$\beta$ 用于偏移；
• 多数情况下，如果模型的第一层使用了 BN 层，可省略标准化和归一化相关操作（比如使用StandardScaler）
• BN 层做对小批量输入了进行标准化工作（虽然是估算的，每次只处理一个批次，但能做缩放和平移）
• BN层为每个输入添加了四个参数量，分别是：
  • 可训练的、可通过反向传播学习的 $\gamma$ 参数（输出缩放矢量）和 $\beta$ 参数（输出偏移矢量），
  • 不可训练的、使用指数移动平均值估计的：$\mu$（最终输入平均值矢量）和 $\sigma$ （最终输入标准差矢量）。注意：$\mu$ 和 $\sigma$ 都是在训练过程中计算的，但只在训练后使用。
• 公式中 $?$ 是很小的数字，防止分母出现0（通常是$10^{?5}$) 。

Ioffe 和 Szegedy 证明 ，批归一化大大改善了他们试验的所有深度神经网络，极大提高了 ImageNet 分类的效果。

梯度消失问题大大减少了。

他们可以使用饱和激活函数，如 tanh 甚至逻辑激活函数sigmoid。网络对权重初始化也不那么敏感。能够使用更大的学习率，显著加快了学习过程。

使用 Keras 实现批归一化

示例代码：

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.BatchNormalization(),  # 这里使用了BN
    keras.layers.Dense(300, activation="relu"),
    keras.layers.BatchNormalization(),
    keras.layers.Dense(100, activation="relu"),
    keras.layers.BatchNormalization(),
    keras.layers.Dense(10, activation="softmax")
])

model.summary()
'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten (Flatten)            (None, 784)               0         
_________________________________________________________________
batch_normalization (BatchNo (None, 784)               3136       
_________________________________________________________________
dense (Dense)                (None, 300)               235500    
_________________________________________________________________
batch_normalization_1 (Batch (None, 300)               1200      
_________________________________________________________________
dense_1 (Dense)              (None, 100)               30100     
_________________________________________________________________
batch_normalization_2 (Batch (None, 100)               400       
_________________________________________________________________
dense_2 (Dense)              (None, 10)                1010      
=================================================================
Total params: 271,346
Trainable params: 268,978
Non-trainable params: 2,368
模型中，
第一个BN层为每个输入特征增加了4个参数：784*4=3136 
第二个BN层为每个输入特征增加了4个参数：300*4=1200
第三个BN层为每个输入特征增加了4个参数：100*4=400
共计：4736，如算法思路，其中不可训练的是2368个
'''


bn1 = model.layers[1]
[(var.name, var.trainable) for var in bn1.variables]

'''
[('batch_normalization/gamma:0', True),
 ('batch_normalization/beta:0', True),
 ('batch_normalization/moving_mean:0', False),
 ('batch_normalization/moving_variance:0', False)]
'''

model.compile(loss="sparse_categorical_crossentropy",
              optimizer=keras.optimizers.SGD(learning_rate=1e-3),
              metrics=["accuracy"])

梯度裁剪

• 缓解梯度爆炸问题的另一种流行技术是在反向传播期间裁剪梯度，使它们不超过某个阈值。
• 梯度裁剪在循环神经网络中用的很多，因为循环神经网络中用 BN 很麻烦。

在 Keras 中，梯度裁剪只需在创建优化器时设置 clipvalue 或 clipnorm 参数，

示例代码：

#All Keras optimizers accept clipnorm or clipvalue arguments:

optimizer = keras.optimizers.SGD(clipvalue=1.0)  # 超参数，阈值
optimizer = keras.optimizers.SGD(clipnorm=1.0)   # 超参数，确保梯度裁剪不改变梯度矢量的方向

如果在训练过程中发现了梯度爆炸（可以用 TensorBoard 跟踪梯度），最好的方法是既用值也用范数裁剪，设置不同的阈值，看看哪个在验证集上表现最好。

复用预训练层

从零开始训练一个非常大的 DNN通常不是好的思路，相反，应该尝试找到一个现有的神经网络来完成与其类似的新任务，方法就是要：复用这个现有网络的较低层：这就是所谓的迁移学习。这样不仅能大大加快训练速度，还将需要更少的训练数据。如图：

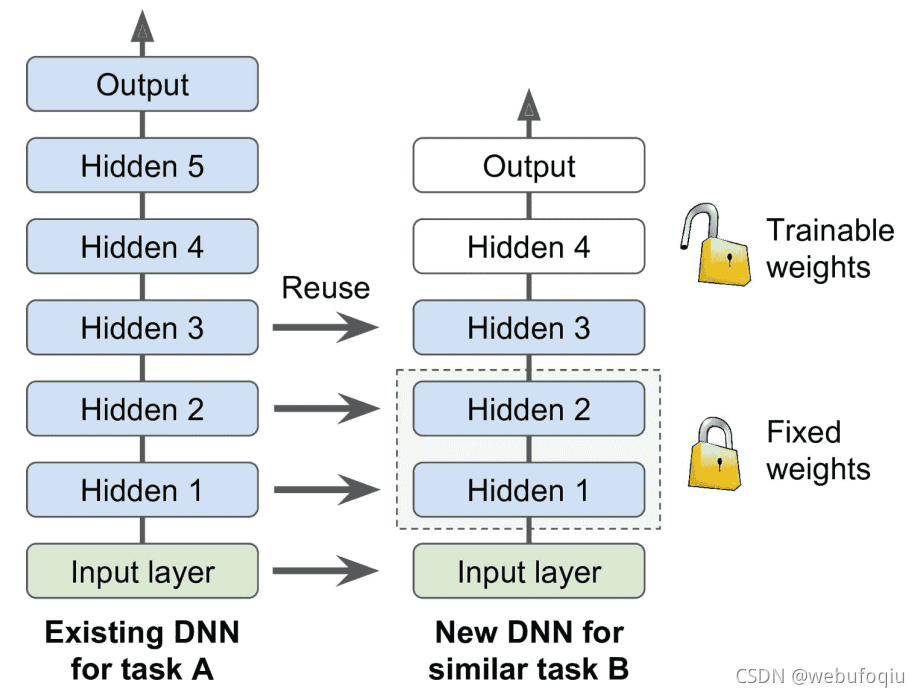
• 添加必要的预处理步骤将输入特征的大小调整为原始模型的预期大小。也就是说，新任务的输入特征具有类似的低级层次的特征，则迁移学习将更好地工作。

• 原始模型的输出层通常都要替换掉，同理，原始模型的上层也不如浅层管用，因为高阶特征可能相差很大。需要提前确定好，到底用几层。

• 任务越相似，可复用的层越多。对于非常相似的任务，可以尝试保留所有的隐藏层，替换输出层。

• 先将所有复用的层冻结（即，使其权重不可训练，梯度下降不能修改权重），然后训练模型，看其表现如何。

• 然后将复用的最上一或两层解冻，让反向传播可以调节它们，再查看性能有无提升。训练数据越多，可以解冻的层越多。解冻时减小学习率也有帮助，可以避免破坏微调而得的权重。

• 如果效果不好，或者训练数据不多，可以尝试去除顶层，将其余的层都解冻。不断尝试，直到找到合适的层，如果训练数据很多，可以尝试替换顶层，或者加入更多的隐藏层。

用 Keras 进行迁移学习

示例代码：

已有不错的模型A：假设 Fashion MNIST 只有八个类，不包括拖鞋和 T 恤。已经搭建并训练了模型，且效果不错（9x%）

任务：训练新模型B：有拖鞋和 T 恤的图片，要训练一个二分类器（positive=shirt, negative=sandal）。数据集不大，只有 200 张打了标签的图片。

model_A = keras.models.load_model("my_model_A.h5") #调用训练好的模型A
model_A_clone = keras.models.clone_model(model_A) #复制
model_A_clone.set_weights(model_A.get_weights()) 

model_B_on_A = keras.models.Sequential(model_A.layers[:-1])
model_B_on_A.add(keras.layers.Dense(1, activation="sigmoid"))  #替换输出层

for layer in model_B_on_A.layers[:-1]:
    layer.trainable = False   #冻结为不可训练

model_B_on_A.compile(loss="binary_crossentropy",
                     optimizer=keras.optimizers.SGD(lr=1e-3),
                     metrics=["accuracy"])

history = model_B_on_A.fit(X_train_B, y_train_B, epochs=4,
                           validation_data=(X_valid_B, y_valid_B))

for layer in model_B_on_A.layers[:-1]:
    layer.trainable = True

model_B_on_A.compile(loss="binary_crossentropy",
                     optimizer=keras.optimizers.SGD(lr=1e-3),
                     metrics=["accuracy"])
history = model_B_on_A.fit(X_train_B, y_train_B, epochs=16,
                           validation_data=(X_valid_B, y_valid_B))

#[0.06814692169427872, 0.9934999942779541]

迁移学习在深度卷积网络中表现最好，CNN 学到的特征更通用（特别是浅层）

无监督预训练

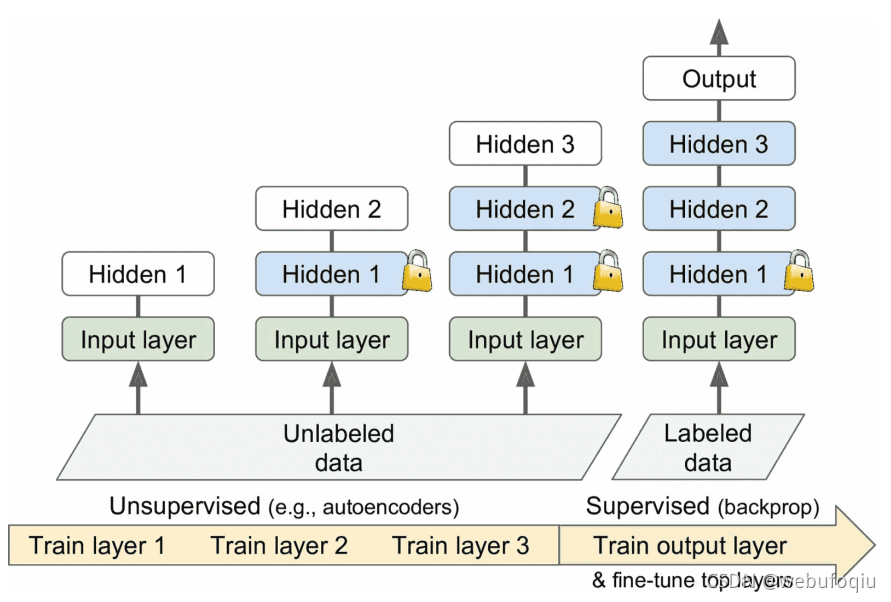
先训练一个单层无监督模型，通常是 RBM(受限玻尔兹曼机)，然后冻结该层，加另一个层，再训练模型（只训练新层），然后冻住新层，再加一层，再次训练模型。现在变得简单了，训练完整的无监督模型，使用的是自编码器或 GAN（生成对抗网络）。

在辅助任务上预训练

如果你想建立一个识别面孔的系统，你可能只有几个人的照片 - 显然不足以训练一个好的分类器。 收集每个人的数百张照片将是不实际的。 但是，您可以在互联网上收集大量随机人员的照片，并训练第一个神经网络来检测两张不同的照片是否属于同一个人。 这样的网络将学习面部优秀的特征检测器，所以重复使用它的较低层将允许你使用很少的训练数据来训练一个好的面部分类器。

再比如：对于自然语言处理（NLP），可以下载大量文本，然后自动生成标签数据。例如，可以随机遮挡一些词，然后训练一个模型预测缺失词。如果能在这个任务上训练一个表现不错的模型，则该模型已经在语言层面学到不少了，就可以复用它到实际任务中，再用标签数据微调

更快的优化器（加速梯度下降）

四种加速训练的方法:

• 对连接权重应用良好的初始化策略
• 使用良好的激活函数
• 使用批归一化
• 重用预训练网络

另一个速度提升的方法是使用更快的优化器，而不是常规的梯度下降优化器。

结论是，几乎总是应该使用Adam_optimization ,需要这么小的改动，训练通常会快几倍。

动量优化

梯度下降只是通过直接减去：损失函数 $J(\theta )$ 相对于权重 $\theta$ 的梯度 ${?}_{\theta }J(\theta )$乘以学习率 $\eta$ 来更新权重 $\theta$ 。它不关心早期的梯度是什么， 如果局部梯度很小，则会非常缓慢。

Boris Polyak 在 1964 年提出的动量优化背后的一个非常简单的想法

改造梯度下降公式：
$$
普通梯度下降\

\theta\leftarrow\theta - \eta \nabla_{\theta} J(\theta) \
动量优化：\
m\leftarrow \beta m+ \eta \nabla_{\theta} J(\theta) \
\theta \leftarrow \theta -m\
\beta 是动量，必须设置在0-1之间，典型的动量值是0.9\
$$
示例代码：

optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9)

动量优化的一个缺点是它增加了另一个超参数来调整。 然而，0.9 的动量值通常在实践中运行良好，几乎总是比梯度下降快。

Nesterov 加速梯度

Yurii Nesterov 在 1983 年提出的动量优化的一个小变体几乎总是比普通的动量优化更快。

Nesterov Accelerated Gradient 简称：NAG
$$\begin{gathered} Nesterov加速梯度： \\ m\leftarrow \beta m+\eta {?}_{\theta }J(\theta +\beta m) \\ \theta \leftarrow \theta ?m \\ 与普通的动量优化的唯一区别在于梯度是在\theta +\beta m而不是在\theta 处测量的 \end{gathered}$$
示例代码：

optimizer = keras.optimizers.SGD(lr=0.001, momentum=0.9, nesterov=True)

AdaGrad 算法

梯度下降从最陡峭的斜坡快速下降，然后缓慢地下到谷底。 如果算法能够早期检测到这个问题并且纠正它的方向来指向全局最优点，那将是非常好的。AdaGrad 算法通过沿着最陡的维度缩小梯度向量来实现这一点:
$$
s\leftarrow s+\nabla_{\theta} J(\theta ) \otimes \nabla_{\theta} J(\theta )\

\theta \leftarrow \theta-\eta \nabla_{\theta} J(\theta ) \oslash \sqrt{s+\epsilon}\

\\epsilon：避免除零的平滑项，一般取10^{-10}\
\otimes 逐元素相乘
\oslash 逐元素相除
$$
这种算法会降低学习速度，但对于陡峭的维度，其速度要快于具有温和的斜率的维度。 这被称为自适应学习率。 它有助于将更新的结果更直接地指向全局最优。

另一个好处是它不需要那么多的去调整学习率超参数 $\eta$ 。

RMSProp 算法

AdaGrad 的风险是降速太快，可能无法收敛到全局最优。

RMSProp 算法通过仅累积最近迭代（而不是从训练开始以来的所有梯度）的梯度来修正这个问题。
$$\begin{gathered} s\leftarrow \beta s+(1?\beta ){?}_{\theta }J(\theta )?{?}_{\theta }J(\theta ) \\ \theta \leftarrow \theta ?\eta {?}_{\theta }J(\theta )?\sqrt{s+?} \\ \beta 又是新的超参数，通常也设置为0.9 \end{gathered}$$

optimizer = keras.optimizers.RMSprop(lr=0.001, rho=0.9) 
rho：对应公式中的beta

经典的 Adam 和 Nadam 优化

Adam，代表自适应矩估计，结合了动量优化和 RMSProp 的思想：就像动量优化一样，它追踪过去梯度的指数衰减平均值，就像 RMSProp 一样，它跟踪过去平方梯度的指数衰减平均值 。
$$\begin{gathered} m={\beta }_{1}m+(1?{\beta }_1){?}_{\theta }J(\theta ) \\ s={\beta }_{2}s+(1?{\beta }_2){?}_{\theta }J(\theta )?{?}_{\theta }J(\theta ) \\ \hat{m}=\frac{m}{1?{\beta }_1^T} \\ \hat{s}=\frac{s}{1?{\beta }_2^T} \\ \theta =\theta +\eta \hat{m}?\sqrt{\hat{s}+?} \\ T代表迭代次数（从1开始） \\ 动量衰减超参数\beta 1通常初始化为0.9，而缩放衰减超参数\beta 2通常初始化为0.999 \\ 平滑项\epsilon 通常被初始化为一个很小的数，例如10^{?7} \end{gathered}$$
示例代码：

optimizer = keras.optimizers.Nadam(lr=0.001, beta_1=0.9, beta_2=0.999)

Nadam 优化是 Adam优化加上Nesterov 技巧。因此收敛速度通常比 Adam稍快。但，有时总体上不如RMSprop

学习率调度

如图：找到一个好的学习率非常重要。

• 如果设置太高，训练可能会发散。
• 如果设置得太低，训练最终会收敛到最佳状态，但会花费很长时间。
• 如果将其设置得稍高，开始的进度会非常快，但最终会在最优解周围跳动，永远不会停下来。如果计算资源有限，可能需要打断训练，在最优收敛之前拿到一个次优解。

如图，除了固定学习率，还有更好的策略：如果你从一个高的学习率开始，然后一旦它停止快速的进步就减少它，比固定学习率更快地达到一个好的解决方案。

常用的学习率调整策略：

• 幂调度(decay 创建优化器时使用超参数decay=s(学习率除以多个数字单位所需要的步数)的倒数)

optimizer = keras.optimizers.SGD(lr=0.001, decay=1e-4)

• 指数调度
• 分段恒定调度
• 性能调度
• 1周期调度（1循环调度）

通过正则化避免过拟合

L1或L2 正则化

layer = keras.layers.Dense(100, activation="elu",
                           kernel_initializer="he_normal",
                           kernel_regularizer=keras.regularizers.l2(0.01))

dropout正则化

dropout 是深度神经网络最流行的正则化方法之一。

它由 Geoffrey Hinton 于 2012 年提出，并在 Nitish Srivastava 等人的 2014 年论文中进一步详细描述，并且已被证明是非常成功的。

基本思想：

在每个训练步骤中，每个神经元（包括输入神经元，但不包括输出神经元）都有一个暂时“删除”的概率: $P$，

这意味着在这个训练步骤中某些神经元会被完全忽略， 在下一步训练步骤中可能又会处于活跃状态。

超参数 $P$ 称为丢失率，通常设为 10%到 50%之间；循环神经网络之间接近 20-30%；在卷积网络中接近 40-50%。

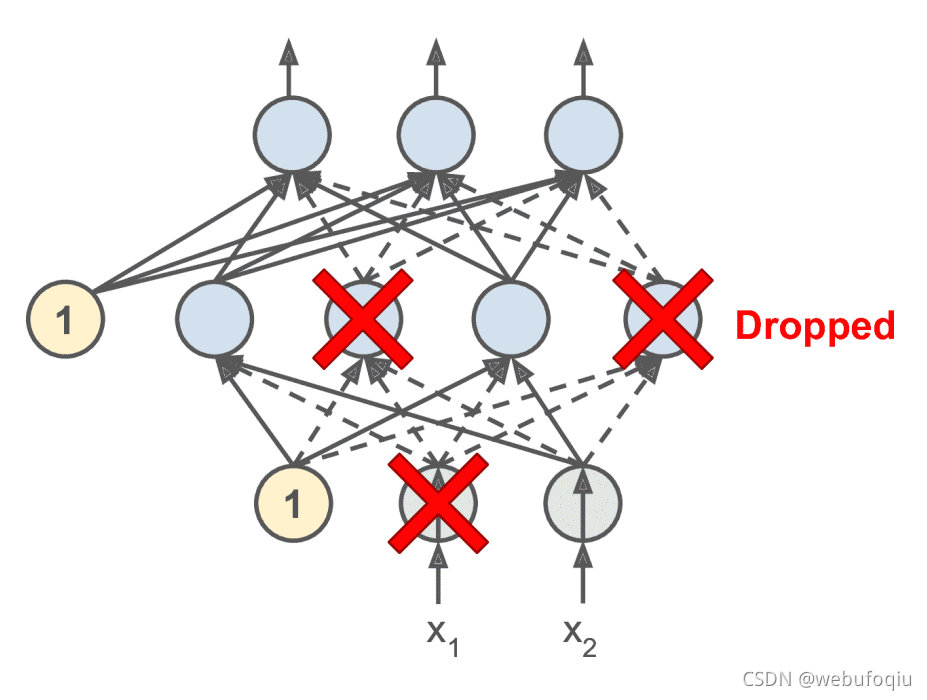
实例代码：

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(300, activation="elu", kernel_initializer="he_normal"),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"),
    keras.layers.Dropout(rate=0.2),
    keras.layers.Dense(10, activation="softmax")
])
#在每个全连接层之前添加Dropout层，丢弃率=0.2

蒙特卡洛（MC）dropout

它可以提升任何训练过的 dropout 模型的性能，并且无需重新训练或修改，对模型存在的不确定性提供了一种更好的方法，也很容易实现。

MC dropout 是一个可以提升 dropout 模型、提供更加不准确估计的神奇方法。

代码示例

y_probas = np.stack([model(X_test_scaled, training=True) for sample in range(100)])
y_proba = y_probas.mean(axis=0)

最大范数正则化

另一种在神经网络中非常流行的正则化技术被称为最大范数正则化：对于每个神经元，它约束输入连接的权重 $W$，使得L2范数： $||W|{|}_2\le r$，其中 $r$ 是最大范数超参数。

要在Keras 中实现最大范数正则，需要设置每个隐藏层的kernel_constraint的max_norm()为一个合适的值，如下代码：

keras.layers.Dense(100, activation="elu", kernel_initializer="he_normal"  kernel_constraint=keras.constraints.max_norm(1.))
'''
每次训练迭代之后，模型的fit()方法会调用max_norm()返回的对象，将层的权重传给该对象，并获得返回的缩放过的权重，然后替换该层的权重。
'''

总结

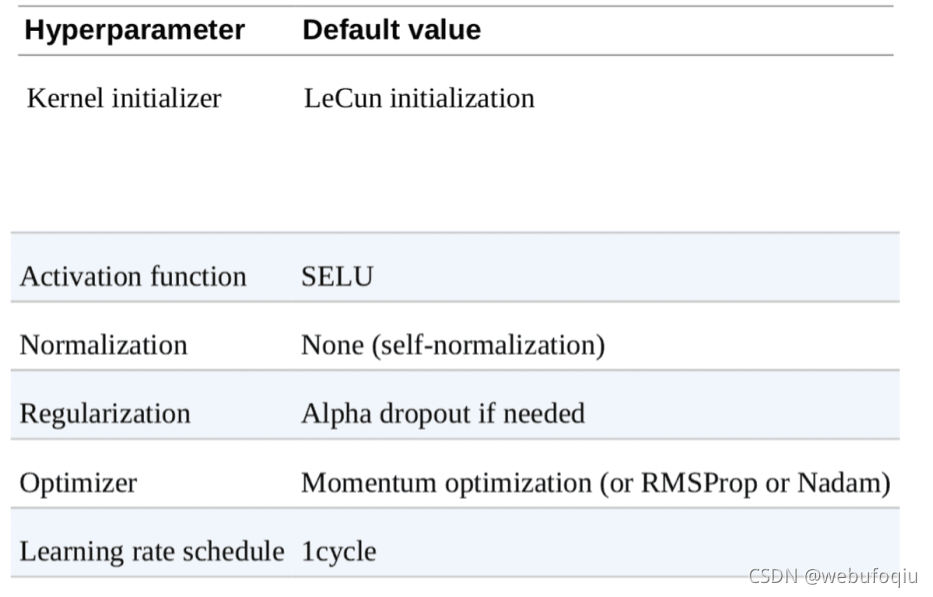
默认的DNN配置

如果网络只有DENSE全连接层，自归一化网络的 DNN 配置