1.分类算法
1.1 sklearn转换器与估计器
1.1.1 转换器(在特征工程中使用)
特征工程中的步骤:
- 1.实例化(实例化一个转换器类(Transformer))
- 2.调用fit_transform(对于文档建立分类词频矩阵,不能同时调用)
- 先计算出每一列的平均值、标准差
- 再通过标准化公式: X ′ = x ? m e a n σ X'=\frac{x-mean}{\sigma } X′=σx?mean? 进行最终的转换。
1.1.2 估计器(sklearn机器学习算法的实现)
在sklearn中,估计器(estimator)是一类实现了算法的API。
- 用于分类的估计器:
- sklearn.neighbors k-近邻算法
- sklearn.naive_bayes 贝叶斯
- sklearn.linear_model.LogisticRegression 逻辑回归
- sklearn.tree 决策树与随机森林
- 用于回归的估计器:
- sklearn.linear_model.LinearRegression 线性回归
- sklearn.linear_model.Ridge 岭回归
- 用于无监督学习的估计器:
- sklearn.cluster.KMeans 聚类
估计器工作流程:
- 实例化一个estimator
- estimator.fit(x_train,y_train) 计算(调用完毕,模型生成)
- 模型评估:
- 直接比对真实值和预测值
- y_predict = estimator.predict(x_test)
- y_test = y_predict
- 计算准确率
- accuracy = estimator.score(x_test,y_test)
- 直接比对真实值和预测值
1.2 K-邻近算法
根据你的邻居来推断出你的类别。
定义: 如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。
距离公式: 如点 a(a1,a2,a3)、b(b1,b2,b3),两个样本的距离可以通过如下公式计算:
- 欧氏距离: ( a 1 ? b 1 ) 2 + ( a 2 ? b 2 ) 2 + ( a 3 ? b 3 ) 2 \sqrt{(a1-b1)^2+(a2-b2)^2+(a3-b3)^2} (a1?b1)2+(a2?b2)2+(a3?b3)2?
- 曼哈顿距离: ∣ a 1 ? b 1 ∣ + ∣ a 2 ? b 2 ∣ + ∣ a 3 ? b 3 ∣ |a1-b1|+|a2-b2|+|a3-b3| ∣a1?b1∣+∣a2?b2∣+∣a3?b3∣
- 明可夫斯基距离:是欧氏距离和曼哈顿距离的推广。
API:
- sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)
- n_neighbors:int,可选择(默认为5),k_neighbors查询默认使用的邻居数。
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,'brute’},可选用于计算最近邻居的算法:‘ball_tree’ 将会使用BallTree,'kd_tree’将会使用KDTree,‘auto’将尝试根据传递给fit方法的值来决定最适合的算法。(不同实现方法将影响效率)
案例1:鸢尾花种类预测
iris数据集是常用的分类实验数据集,它的具体介绍:
- 实例数量:150(三个类各有50)
- 属性数量:4(数值型、数值型、帮助预测的属性和类)
- Attribute Information:
- sepal length 萼片长度(cm)
- sepal width 萼片宽度
- petal length 花瓣长度
- petal width 花瓣宽度
- class:
- Iris-Setose 山鸢尾
- Iris-Versicolour 变色鸢尾
- Iris-Virginica 维吉尼亚鸢尾
流程分析:
- 获取数据
- 数据集划分(一部分训练,一部分用于测试)
- 特征工程
- 标准化
- KNN预估器流程
- 模型评估
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
def knn_iris():
"""
用knn算法对鸢尾花进行分类
:return:
"""
# 1.获取数据
iris = load_iris()
# 2.数据集划分(一部分训练,一部分用于测试)
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
# print("训练集:x_train\n", x_train)
# print("训练集:y_train\n", y_train)
# print("测试集:x_test:\n", x_test)
# 3.特征工程:标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# print(x_train)
# print(x_test)
# 4.KNN预估器流程
# 实例化一个预估器类
estimator = KNeighborsClassifier(n_neighbors=3)
estimator.fit(x_train, y_train)
# 5.模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值与预测值:\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
return None
if __name__ == "__main__":
# 用knn算法对鸢尾花进行分类
knn_iris()
总结:
- 优点:简单,易于理解,易于实现,无需训练
- 缺点:
- 必须指定K值,K值选择不当则分类精度不能保证。
- 懒惰算法,对测试样本分类时的计算量大,内存开销大。
- 应用场景:小数据场景,几千~几万数据场景。
1.3 模型选择与调优
交叉验证:
- 将拿到的训练数据,分为训练和验证集。(就是把训练数据分为n份,差不多均分吧,把其中一份作为验证集,其他作为训练集,进行测试。然后每一份都做一次验证集,得到n个模型的结果,取它们的平均值,这就叫做n折交叉验证。)
交叉验证目的: 让被评估的模型更加准确可信。
超参数搜索—网格搜索
- 有的参数是需要手动指定的,这种叫超参数。
- 手动指定会有各种问题而且复杂。所以对模型预设几种超参数组合。每种超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。
模型选择与调优API:
- sklearn.model_selection.GrideSearchCV(estimator,param_grid=None,cv=None)
- 对估计器的指定参数值进行详尽搜索
- estimator:估计器对象
- param_grid:估计器参数(dict){“n_neighbors”: [1,3,5]}
- cv:指定几折交叉验证
- fit():输入训练数据
- score():准确率
- 结果分析:
- 最佳参数:best_params_
- 最佳结果:best_score_
- 最佳估计器:best_estimator_
- 交叉验证结果:cv_results_
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
def knn_iris_gscv():
"""
用knn算法对鸢尾花进行分类,添加网格搜索和交叉验证
:return:
"""
# 1.获取数据
iris = load_iris()
# 2.数据集划分(一部分训练,一部分用于测试)
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
# print("训练集:x_train\n", x_train)
# print("训练集:y_train\n", y_train)
# print("测试集:x_test:\n", x_test)
# 3.特征工程:标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# print(x_train)
# print(x_test)
# 4.KNN预估器流程
# 实例化一个预估器类
estimator = KNeighborsClassifier()
# 加入网格搜索和交叉验证
# 准备参数
param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
estimator = GridSearchCV(estimator, param_grid=param_dict, cv=10)
estimator.fit(x_train, y_train)
# 5.模型评估
# 方法1:直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值与预测值:\n", y_test == y_predict)
# 方法2:计算准确率
score = estimator.score(x_test, y_test)
print("准确率为:\n", score)
# 最佳参数:best_params_
print("最佳参数:\n", estimator.best_params_)
# 最佳结果:best_score_
print("最佳结果:\n", estimator.best_score_)
# 最佳估计器:best_estimator_
print("最佳估计器:\n", estimator.best_estimator_)
# 交叉验证结果:cv_results_
print("交叉验证结果:\n", estimator.cv_results_)
return None
if __name__ == "__main__":
# 用knn算法对鸢尾花进行分类,添加网格搜索和交叉验证
knn_iris_gscv()
案例:预测Facebook签到位置
流程分析:
- 获取数据
- 数据处理
- 目的:
- 特征值
- 目标值
- time -处理成->年月日,时分秒
- 过滤签到次数少的地点
- 目的:
- 特征工程:标准化
- KNN算法预估流程
- 模型选择与调优
- 模型评估
1.4 朴素贝叶斯算法
1.4.1联合概率、条件概率与相互独立
- 联合概率:包含多个条件,且所有条件同时成立的概率。
- 记作P(A)
- 条件概率:就是事件A在另一个事件B已经发生条件下的概率。
- 记作P(A|B)
- 相互独立:如果P(A,B) = P(A)P(B),则称事件A与事件B相互独立。
1.4.2贝叶斯公式
P ( C ∣ W ) = P ( W ∣ C ) P ( C ) P ( W ) P(C|W) = \frac{P(W|C)P(C)}{P(W)} P(C∣W)=P(W)P(W∣C)P(C)?
- W是给定文档的特征值(频率统计,预测文档提供),C为文档类别。
在文章分类的场景中,这个公式可以这样解读:
P
(
C
∣
F
1
,
F
2
,
F
3
,
.
.
.
)
=
P
(
F
1
,
F
2
,
F
3
,
.
.
.
∣
C
)
P
(
C
)
P
(
F
1
,
F
2
,
F
3
,
.
.
.
)
P(C|F1,F2,F3,...) = \frac{P(F1,F2,F3,...|C)P(C)}{P(F1,F2,F3,...)}
P(C∣F1,F2,F3,...)=P(F1,F2,F3,...)P(F1,F2,F3,...∣C)P(C)?
- P(C ):每个文档类别的概率(某文档类别数/总文档数量)
- P(W|C):在给定类别下特征(被预测文档中出现的词)的概率。
- 计算方法:P(F1 | C)=Ni / N(训练文档中去计算)
- Ni为该F1词在C类别所在文档中出现的次数。
- N为所属类别C下的文档所有词出现的次数和。
- 计算方法:P(F1 | C)=Ni / N(训练文档中去计算)
- P(F1, F2, …)预测文档中每个词的概率。
朴素贝叶斯:朴素+贝叶斯
- 朴素:就是假设特征与特征之间是相互独立的。
- 贝叶斯:就是贝叶斯公式。
应用场景:
- 文本分类
- 单词作为特征
文章分类计算案例:
| 文档ID | 文档中的词 | 属于c=China类 | |
|---|---|---|---|
| 训练集 | 1 | Chinese Beijing Chinese | Yes |
| 2 | Chinese Chinese Shanghai | Yes | |
| 3 | Chinese Macao | Yes | |
| 4 | Tokyo Japan Chinese | No | |
| 测试集 | 5 | Chinese Chinese Chinese Tokyo Japan | ? |
通过朴素贝叶斯来计算测试集是否属于China类
P
(
C
∣
F
1
,
F
2
,
F
3
,
.
.
.
)
=
P
(
F
1
,
F
2
,
F
3
,
.
.
.
∣
C
)
P
(
C
)
P
(
F
1
,
F
2
,
F
3
,
.
.
.
)
P(C|F1,F2,F3,...) = \frac{P(F1,F2,F3,...|C)P(C)}{P(F1,F2,F3,...)}
P(C∣F1,F2,F3,...)=P(F1,F2,F3,...)P(F1,F2,F3,...∣C)P(C)?
也就是看属于China类的概率大还是不属于China类的概率大。
P
(
C
h
i
n
a
∣
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
T
o
k
y
o
,
J
a
p
a
n
)
=
P
(
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
T
o
k
y
o
,
J
a
p
a
n
∣
C
h
i
n
a
)
P
(
C
h
i
n
a
)
P
(
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
C
h
i
n
e
s
e
,
T
o
k
y
o
,
J
a
p
a
n
)
P(China|Chinese,Chinese,Chinese,Tokyo,Japan) = \frac{P(Chinese,Chinese,Chinese,Tokyo,Japan|China)P(China)}{P(Chinese,Chinese,Chinese,Tokyo,Japan)}
P(China∣Chinese,Chinese,Chinese,Tokyo,Japan)=P(Chinese,Chinese,Chinese,Tokyo,Japan)P(Chinese,Chinese,Chinese,Tokyo,Japan∣China)P(China)?
P ( 非 C h i n a ∣ C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) = P ( C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ∣ 非 C h i n a ) P ( 非 C h i n a ) P ( C h i n e s e , C h i n e s e , C h i n e s e , T o k y o , J a p a n ) P(非China|Chinese,Chinese,Chinese,Tokyo,Japan) = \frac{P(Chinese,Chinese,Chinese,Tokyo,Japan|非China)P(非China)}{P(Chinese,Chinese,Chinese,Tokyo,Japan)} P(非China∣Chinese,Chinese,Chinese,Tokyo,Japan)=P(Chinese,Chinese,Chinese,Tokyo,Japan)P(Chinese,Chinese,Chinese,Tokyo,Japan∣非China)P(非China)?
而通过已给的数据可以得到:
- P(China) = 3 4 \frac{3}{4} 43?
- P(Chinese|China) = 3 7 \frac{3}{7} 73?
- P(Tokyo|China) =
0
8
\frac{0}{8}
80?
- 此时,概率为零,这种情况通常为数据量太小导致,通过拉普拉斯平滑系数来解决。
- 拉普拉斯平滑系数:
- P ( F 1 ∣ C ) = N i + α N + α m P(F1|C) = \frac{Ni + \alpha }{N+\alpha m} P(F1∣C)=N+αmNi+α?
- α \alpha α为指定的系数,一般为1,m为训练文档中统计出的特征词个数。
- 这样就可以得到 P(Tokyo|China) = 1 14 \frac{1}{14} 141?
- P(Japan|China) = 1 14 \frac{1}{14} 141?(与上一个同理)
- 同理,在非China的条件下也可得到各个的概率。
最终可以得到测试集是属于c = China 的结果。
API
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
案例:20类新闻分类
- 获取数据集
- 划分数据集
- 特征工程
- 文本特征抽取
- 朴素贝叶斯预估器流程
- 模型评估
总结:
优点:
- 对缺失数据不太敏感,算法简单,常用于文本分类。
- 分类准确率高,速度快。
缺点:
- 由于使用了样本属性独立性的假设,所以如果特征属性有关联时其效果不佳。
1.5 决策树
如何高效的进行决策?
- 特征的先后顺序
信息论
1.原理:
- 信息熵、信息增益等。
2.信息熵的定义
- H的专业术语称之为信息熵,单位为比特。
H ( X ) = ? ∑ i ? 1 n P ( x i ) log ? b P ( x i ) H( X ) = - \sum_{i-1}^{n} P( x_i )\log_{b}{P(x_i)} H(X)=?i?1∑n?P(xi?)logb?P(xi?)
3.决策树的依据之一–信息增益
- 信息的衡量->信息量->信息熵
定义与公式:
- 特征A对训练数据集D的信息增益g(D,A),定义为集合D的信息熵H(D)与特征A在给定条件下D的信息条件熵H(D|A)之差,即公式为:
g ( D , A ) = H ( D ) ? H ( D ∣ A ) g(D,A) = H(D) - H(D|A) g(D,A)=H(D)?H(D∣A)
公式详解:
-
信息熵的计算:
H ( D ) = ? ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log ? ∣ C k ∣ ∣ D ∣ H(D) = -\sum_{k=1}^{K}\frac{|C_k|}{|D|}\log_{}{\frac{|C_k|}{|D|}} H(D)=?∑k=1K?∣D∣∣Ck?∣?log?∣D∣∣Ck?∣? -
条件熵的计算:
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) = ? ∑ i = 1 n ∣ D i ∣ ∣ D ∣ ∑ k = 1 K ∣ D i k ∣ ∣ D i ∣ log ? ∣ D i k ∣ ∣ D i ∣ H(D|A) =\sum_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i) = -\sum_{i=1}^{n}\frac{|D_i|}{|D|}\sum_{k=1}^{K}\frac{|D_{ik}|}{|D_i|}\log_{}{\frac{|D_{ik}|}{|D_i|}} H(D∣A)=∑i=1n?∣D∣∣Di?∣?H(Di?)=?∑i=1n?∣D∣∣Di?∣?∑k=1K?∣Di?∣∣Dik?∣?log?∣Di?∣∣Dik?∣? -
注: C k C_k Ck? 表示属于某个类别的样本数。
-
信息增益表示得知特征X的信息的不确定性的减少程度使得类Y的信息熵减少的程度。
决策树的其他划分依据
除了信息增益,还有其他方法,但是原理近似。
- ID3:信息增益,最大的准则
- C4.5:信息增益比,最大的准则
- CART:
- 分类树:基尼系数 最小的准则 在sklearn中可以选择划分的默认原则
- 优势:划分更加细致
决策树API
- class sklearn.tree.DecisionTreeClassifier(criterion = ‘gini’ ,max_depth = None, random_state = None)
- 决策树分类器
- criterion:默认是 ‘gini’ 系数,也可以选择信息增益的熵‘entropy’
- max_depth:树的深度大小
- random_state:随机数种子
决策树可视化
1.保存树的结构到dot文件
- sklearn.tree.export_graphviz() 该函数能够导出DOT格式。
- tree.export_graphviz(estimator, out_file = “tree.dot”, feature_names = ["",""])
2.网站显示结构
- http://webgraphviz.com/
- 将得到的dot文件内容粘贴到网页中,就可以显示了。
决策树的优缺点
优点:
- 简单,利于理解,决策树可视化
缺点:
- 决策树学习者可以创建不能很好的推广数据的过于复杂的树,被称为过拟合。
改进:
- 减枝算法cart(决策树API中已经实现,随机森林参数调优有相关介绍)
- 随机森林
注: 企业重要决策,由于决策树很好的分析能力,在决策过程应用较多,可以特征选择。
案例:泰坦尼克号乘客生存预测
流程分析:
- 获取数据
- 数据处理
- 缺失值处理
- 特征值 --> 字典类型
- 准备好特征值,目标值
- 划分数据集
- 特征工程:字典特征抽取
- 决策树预估器流程
- 模型评估
1.6 集成学习算法之随机森林
训练集:N个样本。
特征值,目标值。
M个特征。
随机森林过程原理:
- 随机,两个随机:
- 训练集随机:N个样本中,随机有放回的抽样N个。
- 每棵树的训练集是通过随机又放回抽样得到的。
- bootstrap 随机有放回抽样。
- 特征随机:从M个特征中随机抽取m个特征。
- M >> m
- 可以降维
- 训练集随机:N个样本中,随机有放回的抽样N个。
采取bootstrap抽样
- 为什么随机抽样训练集?
- 如果不进行随机抽样,每棵树的训练集都一样,那么最终训练出来的树分类结果也是一样的。
- 为什么要有放回的抽样?
- 如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是绝对片面的,会导致每棵树训练出来有很大的差异。而随机森林最后分类取决于多棵树的投票表决。
API
- class sklearn.ensemble.RandomForestClassifier(n_estimators = 10, criterion = ‘gini’, max_depth = None, bootstrap = True, random_state = None, min_samples_split = 2)
- 随机森林分类器
- n_estimators:integer ,optional(default = 10)森林里的树木数量 120,200,500,800,1200
- criteria:string,可选(default=‘gini’)分割特征的测量方法
- max_depth:integer或者None,可选(默认=无)树的最大深度5,8,15,25,30
- max_features = “auto” ,每个决策树的最大特征数量。
- if “auto”,then max_features = sqrt(n_features).
- if “sqrt” ,then max_features = sqrt(n_features) (same as “auto”)
- if “log2”,then max_features = log2(n_features).
- if None,then max_features = n_features.
- bootstrap:boolean ,optional(default = True)是否在构建树时使用放回抽样
- min_samples_split:节点划分最少样本数。
- min_samples_leaf:叶子结点最小样本数。
- 超参数:n_estimators,max_depth,min_samples_split,min_samples_leaf
总结
- 在当前所有算法中,具有极好的准确率。
- 能够有效的运行在大数据集上,处理具有高维特征的输入样本,而且不需要降维。
- 能够评估各个特征在分类问题上的重要性。
2.回归与聚类算法
2.1线性回归
线性回归: 是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 特点:只有一个自变量的情况称为单变量回归,多于一个自变量的情况称为多元回归
- 通用公式:
h
(
w
)
=
w
1
x
1
+
w
2
x
2
+
w
3
x
3
+
.
.
.
+
b
=
w
t
x
+
b
h(w) = w_1x_1+w_2x_2+w_3x_3+...+b = w^tx+b
h(w)=w1?x1?+w2?x2?+w3?x3?+...+b=wtx+b
- 其中w,x可以理解为矩阵:
w = ( b w 1 w 2 ) w = \begin{pmatrix} b \\ w_1 \\ w_2 \end{pmatrix} w=???bw1?w2????? , x = ( 1 x 1 x 2 ) x = \begin{pmatrix} 1 \\ x_1 \\ x_2 \end{pmatrix} x=???1x1?x2?????
- 其中w,x可以理解为矩阵:
线性关系一定是线性模型,线性模型不一定是线性关系。
线性模型的x可以不是一次方的。
线性回归的损失和优化
目的:求模型参数。
- 模型参数能够使得预测准确。
真实值与预测值会存在一定的误差,存在误差就可以将误差衡量出来。
损失函数:
J
(
θ
)
=
(
h
w
(
x
1
)
?
y
1
)
2
+
(
h
w
(
x
2
)
?
y
2
)
2
+
.
.
.
+
(
h
w
(
x
m
)
?
y
m
)
2
=
∑
i
?
1
m
(
h
w
(
x
i
)
?
y
i
)
2
J(\theta ) = (h_w(x_1)-y_1)^2 + (h_w(x_2)-y_2)^2 +... +(h_w(x_m)-y_m)^2 = {\textstyle \sum_{i-1}^{m}} (h_w(x_i)-y_i)^2
J(θ)=(hw?(x1?)?y1?)2+(hw?(x2?)?y2?)2+...+(hw?(xm?)?ym?)2=∑i?1m?(hw?(xi?)?yi?)2
- y i y_i yi? 为第i个训练样本的真实值
- h ( x i ) h(x_i) h(xi?) 为第i个训练样本特征值组合预测函数
- 又称为最小二乘法。
- 如何减去损失使我们预测的更加准确?这就是机器学习的自动学习功能在线性回归中的体现。在这里可以通过一些优化方法去优化回归的损失值。
优化算法
优化算法就是为了求得模型当中的w,使得损失值最小
线性回归常用的两种优化算法:
- 正规方程
- w = ( X T X ) ? 1 X T y w = (X^TX)^{-1}X^Ty w=(XTX)?1XTy
- X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
- 缺点:当特征过多过复杂的时候,求解速度太慢,并且得不到结果
- 梯度下降
- w 1 ′ = w 1 ? α δ cot ? ( w 0 + w 1 x 1 ) δ w 1 w_1' = w_1-\alpha \frac{\delta \cot (w_0+w_1x_1)}{\delta w_1} w1′?=w1??αδw1?δcot(w0?+w1?x1?)?
- w 0 ′ = w 0 ? α δ cot ? ( w 0 + w 0 x 1 ) δ w 1 w_0' = w_0-\alpha \frac{\delta \cot (w_0+w_0x_1)}{\delta w_1} w0′?=w0??αδw1?δcot(w0?+w0?x1?)?
- 理解: α \alpha α为学习速率,需要手动指定(超参数), α \alpha α旁边的整体表示方向,沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新w值。
- 使用:面对训练数据十分庞大的任务,能够找到较好的结果。
线性回归API
- sklearn.linear_model.LinearRegression(fit_intercept = True)
- 通过正规方程化
- fit_intercept:是否计算偏置。
- LinearRegression.coef_:回归系数
- LinearRegression.intercept_:偏置
- sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept = True, learning_rate = “invscaling”, eta0 = 0.01)
- SGDRegression类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- loss:损失类型
- loss = “squared_loss” :普遍最小二乘法
- fit_intercept:是否计算偏置。
- learning_rate:string,optional
- 学习率填充
- ‘constant’:eta = eta0
- ‘optimal’:eta = 1.0/(alpha * (t + t0)) [default]
- ‘invscaling’:eta = eta0/ pow(t, power_t)
- power_t = 0.25:存在父类当中
- 对于一个常数值的学习率来说,可以使用learning_rate = ‘constant’ ,并使用eta0来指定学习率。
- SGDRegression.coef_:回归系数
- SGDRegression.intercept_:偏置
波士顿房价预测:
- 获取数据集
- 划分数据集
- 特征工程
- 无量纲化 - 标准化
- 预估器流程
- fit() --> 模型
- coef_ intercept_
- 模型评估
回归的性能评估
均方误差评价机制:
M
S
E
=
1
m
∑
i
=
1
m
(
y
i
?
y
ˉ
)
2
MSE = \frac{1}{m} {\textstyle \sum_{i=1}^{m}} (y^i-\bar{y})^2
MSE=m1?∑i=1m?(yi?yˉ?)2
-
注: y i y^i yi 为预测值, y ˉ \bar{y} yˉ? 为真实值
-
sklearn.metrics.mean_squared_error(y_true, y_pred)
- 均方差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
正规方程和梯度下降的对比:
| 正规方程 | 梯度下降 |
|---|---|
| 不需要选择学习率 | 需要选择 |
| 一次运算得出 | 需要迭代求解 |
| 需要计算方程,事件复杂度高O(n^3) | 特征数量较大可以使用 |
梯度下降优化器
- GD
梯度下降,原始的梯度下降算法需要计算所有样本的值才能够得出梯度,计算量大,所以后面才会有一系列的改进。 - SGD
随机梯度下降,是一个优化方法。它在一次迭代时只考虑一个训练样本。- SGD的优点:
- 高效
- 容易实现
- SGD的缺点
- SGD需要许多超参数:比如正则项参数、迭代数。
- SGD对于特征标准化是敏感的。
- SGD的优点:
- SAG
随机平均梯度法,由于手链的速度太慢,有人提出基于SAG等基于梯度下降的算法。
Scikit-learn:岭回归、逻辑回归等当中都会有SAG优化。
2.2欠拟合与过拟合
过拟合: 训练集上表现的好,测试集上表现的不好。学多了
- 解决办法:正则化
欠拟合: 训练集上表现不好,测试集上表现也不好。学少了
- 解决办法:增加数据的特征数量
正则化类别
- L1正则化
- 作用:可以使得其中一些W的值直接为0,删除 这些特征的影响。
- LASSO回归
- L2正则化
- 作用:可以使得其中一些W的都很小,都接近于0,削弱 某个特征的影响。
- 优点:越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。
- Ridge回归
- 加入L2正则化后的损失函数:
- J ( w ) = 1 2 m ∑ i = 1 m ( h w ( x i ) ? y i ) 2 + λ ∑ j = 1 n w j 2 J(w) = \frac{1}{2m}\sum_{i=1}^{m}(h_w(x_i) - y_i)^2 + \lambda \sum_{j=1}^{n}w_j^2 J(w)=2m1?∑i=1m?(hw?(xi?)?yi?)2+λ∑j=1n?wj2?
- 注:m为样本数,n为特征数。
- 损失函数 + 惩罚系数*惩罚项
- λ \lambda λ:惩罚系数
正则化力度越大,权重系数会越小。
正则化力度越小,权重系数会越大。
2.3线性回归的改进-岭回归
岭回归 ,其实就是一种线性回归,只不过在算法建立回归方程的时候,加上正则化的限制,从而达到解决过拟合的效果。
API
- sklearn.linear_model.Ridge(alpha = 1.0, fit_intercept = True, solver = “auto”, normalize = False)
- 具有L2正则化的线性回归
- alpha:正则化力度,也叫
λ
\lambda
λ(就是惩罚系数)
- λ \lambda λ取值:0~1 1~10
- solver:会根据数据自动选择优化方法
- sag:如果数据集、特征都比较大,选择该随机梯度下降优化
- normalize:数据是否进行标准化
- normalize = False:可以在fit之前调用preprocessing.StandardScaler标准化数据。
- Ridge.coef_:回归权重
- Ridge.intercept_:回归偏置
2.4分类算法-逻辑回归与二分类
逻辑回归的原理
输入
h
(
w
)
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
b
h(w) = w_1x_1 + w_2x_2 + ... + b
h(w)=w1?x1?+w2?x2?+...+b
逻辑回归的输入就是线性回归的输出
激活函数
- sigmoid函数
- g ( θ T x ) = 1 1 + e ? θ T x g(\theta ^T x) = \frac{1}{1+e^{-\theta ^T x}} g(θTx)=1+e?θTx1?
- 分析
- 回归的结果输入到sigmoid函数当中
- 输出结果:[0,1]区间中的一个概率值,默认0.5为阈值
- 逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别,并且这个类别默认标记为1(正例),另外的一个类别会标记为0(反例)
损失及优化
- 损失:逻辑回归的损失,称为对数似然损失,公式如下
- 分开类别:
-
cos
?
t
(
h
θ
(
x
)
,
y
)
=
{
?
l
o
g
(
h
θ
(
x
)
)
?if?
y
=
1
?
l
o
g
(
1
?
h
θ
(
x
)
)
?if?
y
=
0
\cos t(h_\theta (x),y) = \begin{cases} & -log(h_\theta (x))\text{ if } y= 1\\ & -log(1-h_\theta (x))\text{ if } y= 0 \end{cases}
cost(hθ?(x),y)={??log(hθ?(x))?if?y=1?log(1?hθ?(x))?if?y=0?
- 通过图像来了解公式:
- 当 y = 1时:
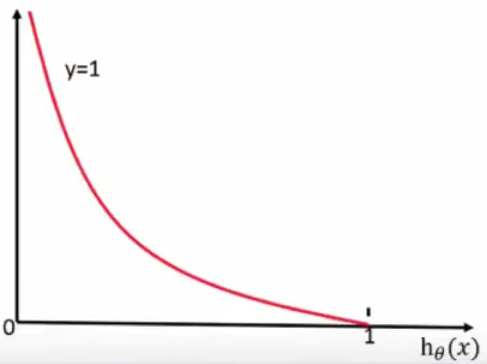
- 当 y = 0时:
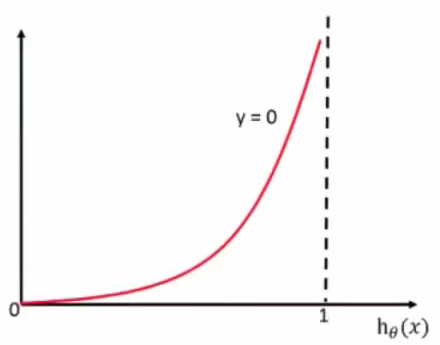
- 综合完整损失函数:
- cos ? t ( h θ ( x ) , y ) = ∑ i = 1 m ? y l o g ( h θ ( x ) ) ? ( 1 ? y i ) l o g ( 1 ? h θ ( x ) ) \cos t(h_\theta (x),y) = \sum_{i=1}^{m} -y log(h_\theta (x)) - (1-y_i)log(1-h_\theta (x)) cost(hθ?(x),y)=∑i=1m??ylog(hθ?(x))?(1?yi?)log(1?hθ?(x))
- 优化
- 同样使用梯度下降优化算法,去减少损失函数的值。这样去更新逻辑回归前面对应算法的权重参数,提升原本属于1类别的概率,减少原本是0类别的概率。
逻辑回归API
- sklearn.linear_model.LogisticRegression(solver = ‘liblinear’ , penalty = ‘l2’,C = 1.0)
- solver:优化求解方式(默认开元的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
- sag:根据数据集自动选择,随机平均梯度下降
- penalty:正则化的种类
- C:正则化力度
- 默认将类别数量少的当做正例
- solver:优化求解方式(默认开元的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数)
- LogisticRegression方法相当于SDGClassifier(loss = ‘log’, penalty = " ")
- SDGClassifier实现了一个普通的随机梯度下降学习,也支持平均随机梯度下降法(ASGD),可以通过设置average = True。而使用LogisticRegression(实现了SAG)。
精确率和召回率
混淆矩阵: 在分类任务下,预测结果与正确标记之间存在四种不同的组合,构成混淆矩阵。
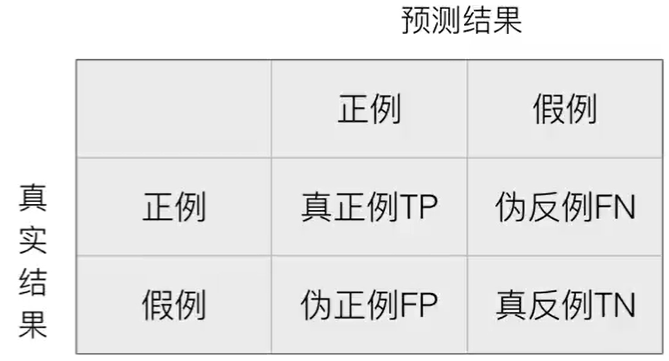
精确率和召回率
精确率:预测结果为正例的样本中真实为正例的比例
召回率:真实为正例的样本中预测结果为正例的比例(看查的全不全)
F1 - score,反映了模型的稳健性
F
1
=
2
T
P
2
T
P
+
F
N
+
F
P
=
2
?
P
r
e
c
i
s
i
o
n
?
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
F1 = \frac{2TP}{2TP+FN+FP} = \frac{2\cdot Precision\cdot Recall}{Precision+Recall}
F1=2TP+FN+FP2TP?=Precision+Recall2?Precision?Recall?
- Precision:精确率
- Recall:召回率
分类评估报告API
- sklearn.metrics.classification_report(y_true, y_pred, labels=[], target_names = None)
- y_true:真实目标值
- y_pred:估计器预测目标值
- labels:指定类别对应的数字
- target_names:目标类别名称
- return:每个类别精确率与召回率
ROC曲线与AUC指标
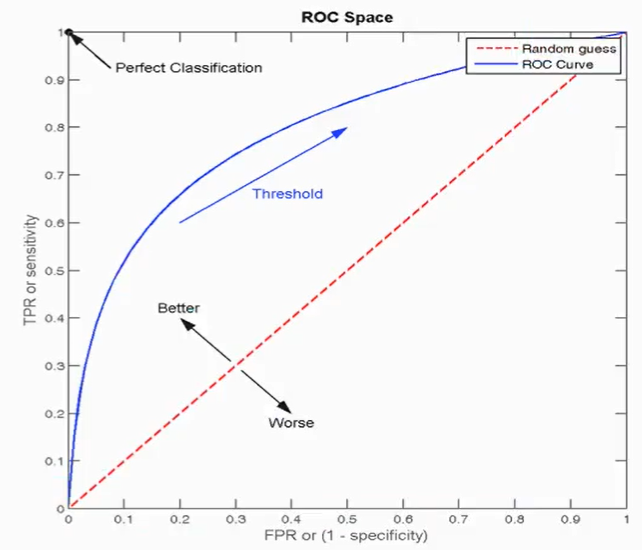
TPR与FPR
- TPR = TP / (TP + FN)(召回率)
- 所有真实类别为1的样本中,预测类别为1的比例。
- FPR = FP / (FP + TN)
- 所有真实类别为0的样本中,预测类别为1的比例。
ROC曲线:就是蓝线
AUC指标:就是x轴与y=1以及ROC曲线围成的面积
- AUC的概率意义是随机取一对正负样本,正样本得分大于负样本的概率。
- AUC的最小值为0.5,最大值为1,取值越大越好。
- AUC=1,完美分类器,采用这个预测模型时不管设定什么阈值都能得出完美预测。绝大多数预测的场合,不存在完美分类器。
- 0.5<AUC<1,优于随机猜测。这个分类器妥善设定阈值的话,能有预测价值。
- 最终AUC的范围在[0.5,1]内,并且越接近1越好。
- 要是小于0.5呢?那就反向预测,那么AUC就等于1-原来的AUC,结果依旧大于0.5。
AUC计算API
- from sklearn.metrics import roc_auc_score
- sklearn.metrics.roc_auc_score(y_true, y_score)
- 计算ROC曲线面积,即AUC值
- y_true:每个样本的真实类别,必须为0(反例),1(正例)标记
- y_score:预测得分,可以是正类的估计概率、置信值或者分类器方法的返回值。
- sklearn.metrics.roc_auc_score(y_true, y_score)
总结:
- AUC只能用来评价二分类
- AUC非常适合评价样本不平衡中的分类器性能
2.5模型保存和加载
sklearn模型的保存和加载API
- from sklearn.externals import joblib
- 保存:joblib.dump(estimator, “test.pkl”)
- 加载:estimator = joblib.load(“test.pkl”)
2.6无监督学习-K-means算法
无监督学习包括算法:
- 聚类:k-means(K均值聚类)
- 降维:PCA
K-means聚类步骤
- 随机设置k个特征空间内的点作为初始的聚类中心。
- 其他的每个点计算他们到k个中心的距离,选择最近的一个聚类中心点作为标记类别。
- 通过第二步,所有的点被分为k个聚类,然后每一个聚类都重新计算出它的的新的中心点(平均值)
- 如果计算得出的新中心点与原中心点一样,那么结束,否则重新进行第二步过程。
K-meansAPI
- sklearn.cluster.KMeans(n_clusters = 8, init = ‘k-means ++’ )
- k_means聚类
- n_clusters:开始的聚类中心数量。
- init:初始化方法,默认为 ‘ k-means ++’
- labels:默认标记的类型,可以和真实值比较
K-means性能评估指标
1.轮廓系数
S
C
i
=
b
i
?
a
i
m
a
x
(
b
i
,
a
i
)
SC_i = \frac{b_i - a_i}{max(b_i,a_i)}
SCi?=max(bi?,ai?)bi??ai??
- 对于每个点i为已聚类数据中的样本, b i 为 i b_i 为 i bi?为i到其他族群的所有样本的距离最小值, a i 为 i a_i为i ai?为i到本身簇的距离平均值。最终计算出所有的样本点的轮廓系数平均值。
- 希望看到 b i > > a i b_i >> a_i bi?>>ai?
2.轮廓系数值分析
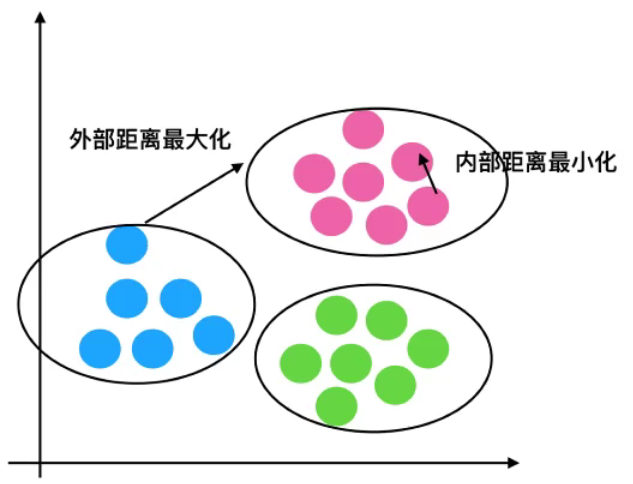
过程分析:
- 蓝1离本身族群所有店距离的平均值 a i a_i ai?
- 蓝1到其他两个族群的距离计算出粉色的平均值和绿色的平均值,取最小的那个平均值作为 b i b_i bi?
- 根据公式:极端值考虑:
- 如果 b i > > a i b_i >> a_i bi?>>ai?,那么公式趋近于1
- 如果 b i < < a i b_i << a_i bi?<<ai?,那么公式趋近于-1
3.结论
- 如果: b i > > a i b_i >> a_i bi?>>ai?:趋近于1效果越好。
- 如果: b i < < a i b_i << a_i bi?<<ai?:趋近于-1效果越差。
- 轮廓系数的值在[-1,1]。
4.轮廓系数API
- sklearn.metrics.silhouette_score(X,labels)
- 计算所有样本的平均轮廓系数
- X:特征值
- labels:被聚类标记的目标值
5.总结
- 特点分析:采用迭代式算法,直观易懂并且非常实用
- 缺点:容易收敛到局部最优解(多次聚类解决)