[人工智能]围棋程序逻辑

机巧围棋(CleverGo)在围棋程序内核上采用了aigagror作者开源的GymGo项目，在该项目的基础上进一步封装了一个训练围棋AI的围棋模拟器。

本文讲解以GymGo项目中相关方法为背景，讲解围棋程序核心方法及实现逻辑。第1部分讲解棋盘状态表示方法；第2部分讲解围棋终局判定方法；第3部分讲解围棋核心规则方法；第4部分综合第3部分的围棋核心规则方法，讲解下一个棋盘状态的计算方法。

1. 棋盘状态表示方法

围棋棋盘由纵横各19条线段组成共361个交叉点，每一个交叉点有存在黑子、存在白子或不存在任何棋子共3中状态。因此，从理论上说，可以用一个二维矩阵表示围棋棋盘状态。如用一个19X19大小的矩阵表示围棋棋盘状态，0表示相应位置不存在棋子，1表示相应位置存在黑子，-1表示相应位置存在白子。

上述棋盘状态表示方法虽然可以完整第表示围棋棋盘状态，但是在编程实践中，采用这种表示方法会使计算一块棋子的气、有效落子位置等方法实现相对困难。在GymGo围棋程序内核中，采用了一种更为合适的表示方式：

用一个Shape为(NUM_CHNLS, SIZE, SIZE)，每个元素的值均为0或1的张量(Tensor)表示围棋棋盘状态，其中NUM_CHNLS的值为6，表示张量的通道数，SIZE表示棋盘的大小。每个通道的数据意义如下：

• CHANNEL[0]：第0通道为BLACK_CHANNEL，表示黑棋棋子分布。有黑棋棋子位置为1，否则为0；
• CHANNEL[1]：第1通道为WHITE_CHANNEL，表示白棋棋子分布。有白棋棋子位置为1，否则为0；
• CHANNEL[2]：第2通道为TURN_CHANNEL，表示下一步落子方，是一个全0或全1的矩阵。0：黑方，1：白方；
• CHANNEL[3]：第3通道为INVLID_CHANNEL，表示下一步的落子无效位置。无效位置为1，其余为0；
• CHANNEL[4]：第4通道为PASS_CHANNEL，表示上一步是否为PASS，是一个全0或全1的矩阵。0：不是PASS，1：是PASS；
• CHANNEL[5]：第5通道为DONE_CHANNEL，表示上一步落子之后，游戏是否终局，是一个全0或全1的矩阵。0：未终局，1：已终局。

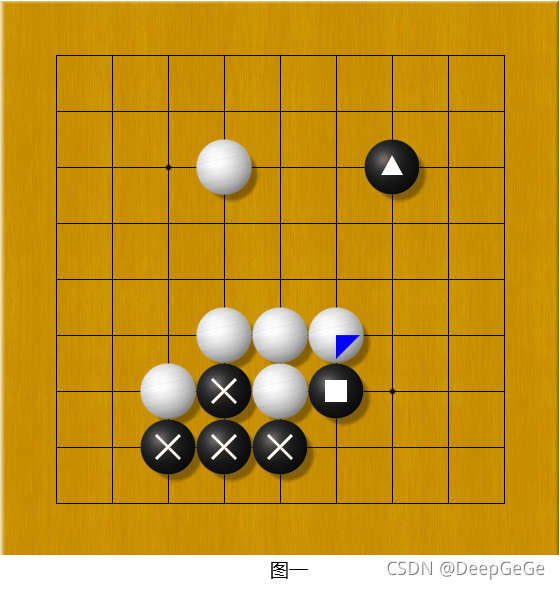
根据上述棋盘状态表示方法，图一所示棋盘状态与相应表示如下：

[[[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 1. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 1. 0. 1. 0. 0. 0.]
  [0. 0. 1. 1. 1. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]

 [[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 1. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 1. 1. 1. 0. 0. 0.]
  [0. 0. 1. 0. 1. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]

 [[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]

 [[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 1. 0. 0. 1. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 1. 1. 1. 0. 0. 0.]
  [0. 0. 1. 1. 1. 1. 0. 0. 0.]
  [0. 0. 1. 1. 1. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]

 [[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]

 [[0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]
  [0. 0. 0. 0. 0. 0. 0. 0. 0.]]]

2. 围棋终局判定方法

根据围棋基本知识一文可知，触发围棋游戏终局共两种情况：一、在对局过程中，黑白行棋双方，有一方认输，即中盘胜/中盘负；二、行棋至某一局面，棋盘上所有地盘归属均划分完毕，行棋双方均认可当前地盘划分现状，即协商终局。

在围棋程序中，可将终局触发的条件设为黑白双方连续PASS。即当上一步落子方为黑方，且黑方选择PASS，接下来白方也选择PASS；当上一步落子方为白方，且白方选择PASS，接下来黑方也选择PASS。

实现终局判定程序逻辑如下：

1. 检查PASS_CHANNEL是否为全1矩阵，并用一个变量previously_passed表明上一步action是否为PASS；
2. 判断下一步action是否为PASS；
    3. 如果为PASS，则将PASS_CHANNEL矩阵置为全1矩阵；
    4. 检查上一步action是否为PASS，即变量previously_passed值是否为True；
        5. 如果上一步action也为PASS，则将DONE_CHANNEL矩阵置为全1矩阵，表明落子之后，游戏终局。

程序实现如下：

# Deep copy the state to modify
state = np.copy(state)

# Initialize basic variables
board_shape = state.shape[1:]  # state.shape为(通道数, 棋盘高度, 棋盘宽度)
pass_idx = np.prod(board_shape)  # np.prod()将参数内所有元素连乘，pass_idx："pass"对应的id
passed = action1d == pass_idx  # 如果action id等于pass_idx，则passed为True
action2d = action1d // board_shape[0], action1d % board_shape[1]  # 将action1d转换成action2d

player = turn(state)  # 获取下一步落子方
previously_passed = prev_player_passed(state)  # 获取上一步是否为pass
ko_protect = None

if passed:
    # We passed
    # 如果下一步为pass，则将next_state中PASS_CHNL矩阵置为全1矩阵
    state[govars.PASS_CHNL] = 1
    if previously_passed:
        # Game ended
        # 如果上一步也为pass，则游戏结束【双方连续各pass，则游戏结束】
        # 将next_state中DONE_CHNL矩阵置为全1矩阵
        state[govars.DONE_CHNL] = 1
else:
    # Move was not pass
    state[govars.PASS_CHNL] = 0

本文中程序实现均只是用程序语言描述围棋程序逻辑，单个代码框中的代码并不一定是一个完整的方法。

3. 围棋核心规则方法

3.1 棋子分块方法

每当在棋盘上添加一颗黑子或白子，则必须判断是否有对手（比如下一步落子方为黑方，则对手为白方，反之亦然）的棋子被杀死，从而更新棋盘状态。

要判断一块棋子是否被杀死，即判断该块棋子的气的数量是否为0。由于一块棋子的气是共用的，即一块棋子同生共死，因此首先必须对棋子分块。

scipy.ndimage.measurements.label()方法可分别对矩阵中成块的元素打上标签。对棋子分块，可以使用该方法直接对不同块棋子打上各不相同的标签，从而对棋子分块。

对图一中黑棋的棋子分块：

from scipy import ndimage
import numpy as np

black_pieces = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 1, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 1, 0, 0, 0],
                         [0, 0, 1, 1, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0]])
all_black_groups, _ = ndimage.measurements.label(black_pieces)
all_black_groups

输出all_black_groups的值如下：

array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 1, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0],
       [0, 0, 0, 2, 0, 3, 0, 0, 0],
       [0, 0, 2, 2, 2, 0, 0, 0, 0],
       [0, 0, 0, 0, 0, 0, 0, 0, 0]])

3. 2 一块棋子气的计算方法

一块棋子的气等同于与该块棋子直接相邻的空交叉点的数量。一块棋子气的计算程序逻辑如下：

1. 计算棋盘上所有空交叉点的分布；
2. 计算该块棋子直接相邻的交叉点分布；
3. 如果一个相邻交叉点为空交叉点，则该交叉点即为该块棋子的气。这样的空交叉点的数量即为该块棋子的气的数量。

3.2.1 棋盘上所有空交叉点的分布矩阵

由于BLACK_CHANNEL对应矩阵为黑棋棋子分布，WHITE_CHANNEL对应矩阵为白棋棋子分布，则将两个矩阵对应元素直接相加，可以得到所有棋子的分布矩阵。用一个全1矩阵减去所有棋子的分布矩阵，即可得到空交叉点的分布矩阵。

from scipy import ndimage
import numpy as np

black_pieces = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 1, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 1, 0, 0, 0],
                         [0, 0, 1, 1, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0]])
white_pieces = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 1, 1, 0, 0, 0],
                         [0, 0, 1, 0, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0]])

all_pieces = np.sum([black_pieces, white_pieces], axis=0)
empties = 1 - all_pieces
empties

输出empties的分布矩阵如下：

array([[1, 1, 1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 0, 1, 1, 0, 1, 1],
       [1, 1, 1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1, 1, 1],
       [1, 1, 1, 0, 0, 0, 1, 1, 1],
       [1, 1, 0, 0, 0, 0, 1, 1, 1],
       [1, 1, 0, 0, 0, 1, 1, 1, 1],
       [1, 1, 1, 1, 1, 1, 1, 1, 1]])

3.2.2 一块棋子直接相邻交叉点的分布矩阵

scipy.ndimage.binary_dilation()方法可将一个矩阵按指定结构膨胀。对图一中X标识的这一块黑棋进行膨胀，可使得X标识的这一块黑棋直接相邻的交叉点的值为True。

from scipy import ndimage
import numpy as np

black_pieces = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 1, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0],
                         [0, 0, 0, 1, 0, 1, 0, 0, 0],
                         [0, 0, 1, 1, 1, 0, 0, 0, 0],
                         [0, 0, 0, 0, 0, 0, 0, 0, 0]])
all_black_groups, _ = ndimage.measurements.label(black_pieces)
x_group = all_black_groups == 2
print('x_group before binary dilation:\n', x_group)

x_group_dilation = ndimage.binary_dilation(x_group)
print('x_group after binary dilation:\n', x_group_dilation)

输出x_group与x_group_dilation矩阵如下：

x_group before binary dilation:
 [[False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False  True False False False False False]
 [False False  True  True  True False False False False]
 [False False False False False False False False False]]
x_group after binary dilation:
 [[False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False False False False False False False]
 [False False False  True False False False False False]
 [False False  True  True  True False False False False]
 [False  True  True  True  True  True False False False]
 [False False  True  True  True False False False False]]

注意，通过scipy.ndimage.binary_dilation()方法不仅使得一块棋子直接相邻的交叉点的值为True，同时也会使得该块棋子中每一个棋子的位置都为True。但是存在棋子的地方必定不是空交叉点，所以不影响后续的气数量的计算。

3.2.3 一块棋子气的分布矩阵

如果一个相邻交叉点为空交叉点，则该交叉点即为该块棋子的气。因此可以使用empties矩阵与x_group_dilation相乘，得到该块棋子气的分布矩阵。计算该气分布矩阵中1的数量，即可得到该块棋子的气。

liberties = empties * x_group_dilation
print('liberties:\n', liberties)
num_liberties = np.sum(liberties)
print('num_liberties:', num_liberties)

输入的气分布矩阵及该块棋子的气数量如下：

liberties:
 [[0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 0 0 0 0 0 0 0 0]
 [0 1 0 0 0 1 0 0 0]
 [0 0 1 1 1 0 0 0 0]]
num_liberties: 5

3.3 棋子分布矩阵更新方法

3.3.1 下一步落子方棋子分布矩阵更新

下一步落子方棋子分布矩阵更新相对简单，可以直接将下一步action转换为棋子分布矩阵坐标，判断该坐标位置是否为有效落子位置，如果是有效落子位置，则将棋子分布矩阵的该位置元素值置为1。

3.3.2 上一步落子方棋子分布矩阵更新

更新上一步落子方棋子分布矩阵，即在下一步落子方落子后，判断上一步落子方是否有棋子被杀死。

当下一步落子方棋子分布矩阵更新完毕，可采取3.2部分所述一块棋子气的计算方法，分别就算上一步落子方在落子位置周围各块棋子的气，将上一步落子方棋子分布矩阵相应中，气为0的各块棋子位置的值置为0。

3.4 劫争的判定方法

根据围棋基本知识一文2.6部分关于劫争的介绍，并进一步分析可知，如果下一步落子方在棋盘上下了一颗棋子之后，上一步落子方被击杀的棋子块数为1，且该块棋子中棋子的个数为1，则上一步落子方被击杀的棋子对应的位置为劫。

因此可在更新上一步落子方棋子分布矩阵时，记录被击杀的各棋子的坐标，并按照上述方法判定棋盘上是否存在劫争。如果存在劫争，则将相应位置打上劫争标记。

3.5 无效落子位置（禁着点）的计算方法

当下一步落子方落子完成后，必须计算下一步落子方的对手的无效落子位置，并更新INVLID_CHANNEL矩阵。

根据围棋规则可知，下一步落子方的对手的无效落子位置满足如下条件：

1. 下一步落子方的对手不能够在如下位置落子：

   • 被占领的位置（即存在棋子的位置，或者说空交叉点）；

   • 劫争标记的位置；

2. 下一步落子方的对手能够在如下位置落子：

   • 如果下一步落子方的对手落子该位置，能够吃掉下一步落子方的棋子；

3. 下一步落子方的对手不能够在如下位置落子：

   • 如果一个空交叉点位置与只有一口气的一块或多块棋子相邻，并且不与超过一口气的一块或多块棋子相邻，且该空交叉点四周都有棋子，则该位置为无效落子位置；

   • 如果一个空交叉点被下一步落子方的棋子包围，且下一步落子方在这个空交叉点周围的相应的各块棋子均有不少于1口气。

围棋中计算无效落子位置的规则相对复杂，如果一时间不能理解，可以暂时先放一边，在学习围棋的过程中会逐步理解上述规则。

无效落子位置的计算逻辑如下：

1. 计算出所有可能的无效落子位置，分为如下情况：
   • 下一步落子方的，所有多于一口气的各块棋的，气的位置；
   • 下一步落子方的对手的，所有只有一口气的各块棋的，气的位置；
2. 计算出在所有可能的无效落子位置中，一定有效的落子位置，分为如下两种情况：
   • 下一步落子方的，所有只有一口气的各块棋的，气的位置；
   • 下一步落子方的对手的，所有多于一口气的各块棋的，气的位置；
3. 计算出所有相邻4个交叉点均存在棋子的位置；
4. 则所有无效的落子位置为：所有存在棋子的位置+在所有可能的无效落子位置中排除掉一定有效的落子位置之后剩下的被完全包围的位置+被劫争标记的位置。

上述无效落子位置的计算逻辑有点难以理解。如果无法理解，请结合围棋规则，多思考，多分析。

无效落子位置的计算程序如下：

def compute_invalid_moves(state, player, ko_protect=None):
    """
    Updates invalid moves in the OPPONENT's perspective
    1.) Opponent cannot move at a location
        i.) If it's occupied（被占领的）
        i.) If it's protected by ko
    2.) Opponent can move at a location
        i.) If it can kill
    3.) Opponent cannot move at a location
        i.) If it's adjacent to one of their groups with only one liberty and
            not adjacent to other groups with more than one liberty and is completely surrounded
        ii.) If it's surrounded by our pieces and all of those corresponding groups
            move more than one liberty
    """

    # All pieces and empty spaces
    # 棋盘所有有棋子的分布矩阵，有棋子的位置为1
    all_pieces = np.sum(state[[govars.BLACK, govars.WHITE]], axis=0)
    # 棋盘上所有空交叉点的分布矩阵，空交叉点位置为1
    empties = 1 - all_pieces

    # Setup invalid and valid arrays
    possible_invalid_array = np.zeros(state.shape[1:])
    definite_valids_array = np.zeros(state.shape[1:])

    # Get all groups
    # 上一步落子方各块棋子分布矩阵，及棋子块数
    all_own_groups, num_own_groups = measurements.label(state[player])
    # 下一步落子方各块棋子分布矩阵，及棋子块数
    all_opp_groups, num_opp_groups = measurements.label(state[1 - player])
    expanded_own_groups = np.zeros((num_own_groups, *state.shape[1:]))
    expanded_opp_groups = np.zeros((num_opp_groups, *state.shape[1:]))

    # Expand the groups such that each group is in its own channel
    for i in range(num_own_groups):
        expanded_own_groups[i] = all_own_groups == (i + 1)

    for i in range(num_opp_groups):
        expanded_opp_groups[i] = all_opp_groups == (i + 1)

    # Get all liberties in the expanded form
    # 计算每一块棋子的气分布矩阵
    # 其中np.newaxis == None，matrix[None]意思是在第0维增加一个维度
    # all_own_liberties和all_opp_liberties均是三维矩阵，代表每块棋子的气的分布
    all_own_liberties = empties[np.newaxis] * ndimage.binary_dilation(expanded_own_groups, surround_struct[np.newaxis])
    all_opp_liberties = empties[np.newaxis] * ndimage.binary_dilation(expanded_opp_groups, surround_struct[np.newaxis])

    # all_own_liberties和all_opp_liberties均是三维矩阵， np.sum( , axis=(1,2))针对每块棋子计算其气数
    # own_liberty_counts和opp_liberty_counts均是一维数组，每个元素代表每块棋的气
    own_liberty_counts = np.sum(all_own_liberties, axis=(1, 2))
    opp_liberty_counts = np.sum(all_opp_liberties, axis=(1, 2))

    # Possible invalids are on single liberties of opponent groups and on multi-liberties of own groups
    # Definite valids are on single liberties of own groups, multi-liberties of opponent groups
    # or you are not surrounded
    possible_invalid_array += np.sum(all_own_liberties[own_liberty_counts > 1], axis=0)
    possible_invalid_array += np.sum(all_opp_liberties[opp_liberty_counts == 1], axis=0)

    definite_valids_array += np.sum(all_own_liberties[own_liberty_counts == 1], axis=0)
    definite_valids_array += np.sum(all_opp_liberties[opp_liberty_counts > 1], axis=0)

    # All invalid moves are occupied spaces + (possible invalids minus the definite valids and it's surrounded)
    surrounded = ndimage.convolve(all_pieces, surround_struct, mode='constant', cval=1) == 4
    invalid_moves = all_pieces + possible_invalid_array * (definite_valids_array == 0) * surrounded

    # Ko-protection
    if ko_protect is not None:
        invalid_moves[ko_protect[0], ko_protect[1]] = 1
    return invalid_moves > 0

4. 下一个棋盘状态的计算方法

给定当前棋盘状态和下一步落子方的action，更新棋盘状态，程序逻辑流程如下：

1. 判断下一步落子方的action是否为PASS，并更新PASS_CHANNEL矩阵和DONE_CHANNEL矩阵；
2. 根据3.3部分所述棋子分布矩阵更新方法，更新BLACK_CHANNEL和WHITE_CHANNEL矩阵；
3. 根据3.4部分所述劫争判定方法，记录劫争标记位置；
4. 根据3.5所述无效落子位置的计算方法，计算下一步落子方的对手的无效落子位置，并更新TURN_CHANNEL矩阵；
5. 更新TURN_CHANNEL矩阵。

具体程序实现如下：

def next_state(state, action1d, canonical=False):
    # Deep copy the state to modify
    state = np.copy(state)

    # Initialize basic variables
    board_shape = state.shape[1:]  # state.shape为(通道数, 棋盘高度, 棋盘宽度)
    pass_idx = np.prod(board_shape)  # np.prod()将参数内所有元素连乘，pass_idx："pass"对应的id
    passed = action1d == pass_idx  # 如果action id等于pass_idx，则passed为True
    action2d = action1d // board_shape[0], action1d % board_shape[1]  # 将action1d转换成action2d

    player = turn(state)  # 获取下一步落子方
    previously_passed = prev_player_passed(state)  # 获取上一步是否为pass
    ko_protect = None

    if passed:
        # We passed
        # 如果下一步为pass，则将next_state中PASS_CHNL矩阵置为全1矩阵
        state[govars.PASS_CHNL] = 1
        if previously_passed:
            # Game ended
            # 如果上一步也为pass，则游戏结束【双方连续各pass，则游戏结束】
            # 将next_state中DONE_CHNL矩阵置为全1矩阵
            state[govars.DONE_CHNL] = 1
    else:
        # Move was not pass
        state[govars.PASS_CHNL] = 0

        # Assert move is valid    检查落子是否有效【state中INVD_CHNL对应位置为0】
        assert state[govars.INVD_CHNL, action2d[0], action2d[1]] == 0, ("Invalid move", action2d)

        # Add piece
        state[player, action2d[0], action2d[1]] = 1

        # Get adjacent location and check whether the piece will be surrounded by opponent's piece
        # 获取下一步落子位置的相邻位置（仅在棋盘内）、下一步落子位置是否被下一步落子方对手的棋子包围
        adj_locs, surrounded = state_utils.adj_data(state, action2d, player)

        # Update pieces
        # 更新棋盘黑白棋子分布矩阵，并返回各组被杀死的棋子列表
        killed_groups = state_utils.update_pieces(state, adj_locs, player)

        # If only killed one group, and that one group was one piece, and piece set is surrounded,
        # activate ko protection
        if len(killed_groups) == 1 and surrounded:
            killed_group = killed_groups[0]
            if len(killed_group) == 1:
                ko_protect = killed_group[0]

    # Update invalid moves
    state[govars.INVD_CHNL] = state_utils.compute_invalid_moves(state, player, ko_protect)

    # Switch turn
    # 设置下一步落子方
    state_utils.set_turn(state)

    # 该标记是选择是否始终以黑棋视角看待当前游戏局面
    if canonical:
        # Set canonical form
        # 该函数将黑白棋子分布对换，并更改下一手落子方为黑棋
        state = canonical_form(state)

    return state

5. 结束语

用程序语言描述围棋规则和逻辑其实并不是很简单，例如一块棋子的气是共同的，因此更新围棋棋盘状态必须找到哪些棋子是一块棋，同时计算这一块棋的气的位置。

在实现机巧围棋时，作者也曾尝试实现一个围棋程序内核，但是如何高效地将棋子分块、计算各块棋子的气，如何准确地计算无效/有效的落子位置，均不是一件很容易的事情。

在作者浏览过的许多围棋程序方法中，GymGo项目采用的直接使用scipy.ndimage.measurements.label()方法对各块棋打标签，采用图像处理中的膨胀方法scipy.ndimage.binary_dilation()计算一块棋子的气的位置，计算所有可能无效落子位置，再进一步排除一定有效落子位置，最终得到无效落子位置等等这些方法非常简单、巧妙且高效，让作者深受启发。

此外，机巧围棋作者也是GymGo项目的Contributor，?乛v乛?嘿嘿。

最后，写这一系列技术原理文档真的不是很简单呀，期望大家能够去GitHub上给机巧围棋点个Star鸭~