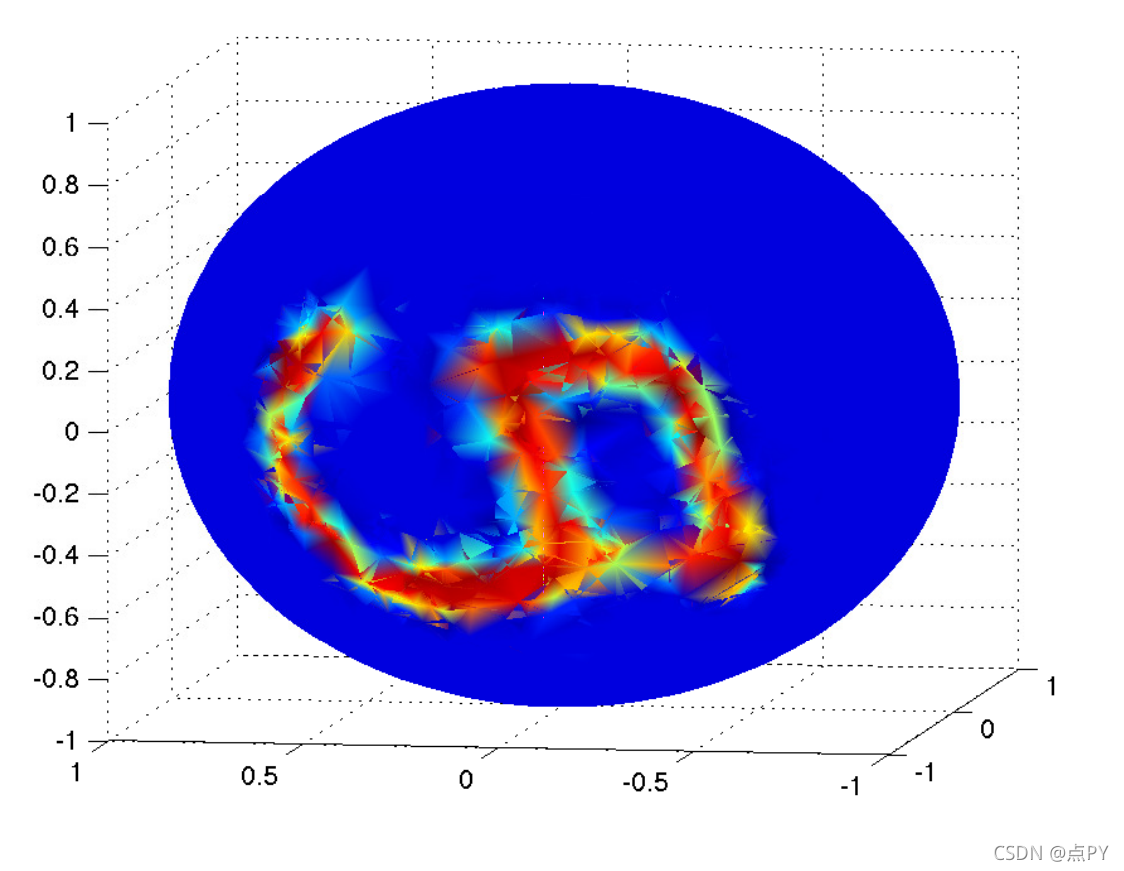
来自 ( Bruna et al., ICLR, 2014 ) 的图描绘了 3D 球体上的 MNIST 图像。虽然很难让卷积网络对球面数据进行分类,但图网络可以自然地处理它。这是一个玩具示例,但在许多实际应用程序中会出现类似的任务。
在我的教程的这一部分中解决的问题是:
1 为什么图表有用?
在许多实际情况下,实际上是由您决定图中的节点和边是什么。
这是一种非常灵活的数据结构,可以泛化许多其他数据结构。例如,如果没有边,那么它就变成了一个集合;如果只有“垂直”边并且任何两个节点都由一条路径连接,那么我们就有了一棵树。这种灵活性有好有坏,我将在本教程中讨论。
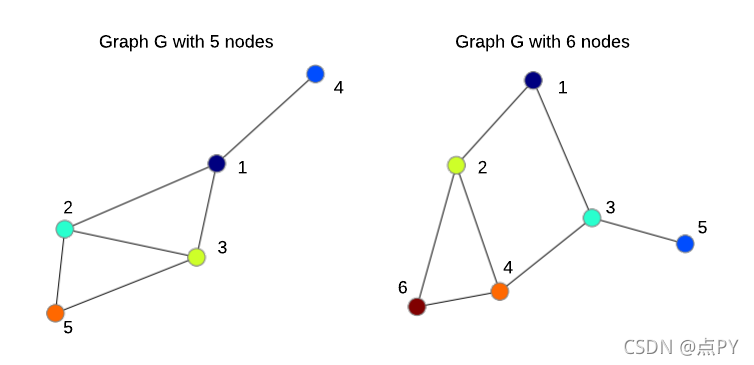
具有 5 个和 6 个节点的两个无向图。节点的顺序是任意的。
在计算机视觉 (CV) 和机器学习 (ML) 的背景下,研究图和从中学习的模型至少可以给我们带来四个好处:
- 我们可以更接近解决以前太具有挑战性的重要问题,例如:癌症药物发现(Veselkov 等,Nature,2019);更好地了解人脑连接组(Diez & Sepulcre,Nature Communications,2019 年);能源和环境挑战的材料发现(谢等人,自然通讯,2019)。
- 在大多数 CV/ML 应用程序中,即使您过去将数据表示为另一种数据结构,数据实际上也可以被视为图形。将您的数据表示为图形可以为您提供很大的灵活性,并且可以为您提供一个非常不同且有趣的视角来看待您的问题。例如,您可以从(Liang 等人,ECCV,2016 年)和我们即将发表的BMVC 论文中的“超像素”中学习,而不是从图像像素中学习。图表还可以让您在数据中施加关系归纳偏差——您对问题的一些先验知识。例如,如果您想对人体姿势进行推理,您的关系偏差可以是人体骨骼关节图(Yan et al., AAAI, 2018); 或者,如果您想对视频进行推理,您的关系偏差可以是移动边界框的图形(Wang 和 Gupta,ECCV,2018 年)。另一个示例可以将面部标志表示为图形(Antonakos 等人,CVPR,2015 年),以对面部属性和身份进行推理。
- 你最喜欢的神经网络本身可以被看作是一个图,其中节点是神经元,边是权重,或者节点是层,边表示前向/后向传递的流(在这种情况下,我们谈论的是 TensorFlow 中使用的计算图, PyTorch 和其他深度学习框架)。应用程序可以是计算图的优化、神经架构搜索、分析训练行为等。
- 最后,您可以解决许多问题,其中数据可以更自然、更有效地表示为图形。这包括但不限于分子和社交网络分类(Knyazev 等人,NeurIPS-W,2018 年)和生成(Simonovsky & Komodakis,ICANN,2018 年)、3D 网格分类和对应关系(Fey 等人,CVPR , 2018)和生成(Wang et al., ECCV, 2018),动态交互对象的建模行为(Kipf et al., ICML, 2018),视觉场景图建模(见即将举行的ICCV Workshop)和问答(Narasimhan, NeurIPS,2018 年),程序合成(Allamanis 等人,ICLR,2018 年))、不同的强化学习任务 ( Bapst et al., ICML, 2019 ) 和许多其他令人兴奋的问题。
2 为什么图上的卷积很难定义?
为了回答这个问题,我首先给出一般使用卷积的一些动机,然后使用图术语描述“图像卷积”,这应该使向“图卷积”的过渡更加平滑。
2.1 为什么卷积有用?
让我们了解为什么我们如此关心卷积以及我们为什么要将其用于图形。与完全连接的神经网络(又名 NN 或 MLP)相比,卷积网络(又名 CNN 或 ConvNets)具有某些优势,下面基于一辆漂亮的老雪佛兰的图像进行解释。

首先,ConvNets 利用图像中的自然先验,在 ( Bronstein et al., 2016 ) 中有更正式的描述,例如:
- Shift-invariance——如果我们将上图中的汽车向左/右/上/下平移,我们仍然应该能够检测到并将其识别为汽车。这是通过在所有位置共享过滤器来利用的,即应用卷积。
- 局部性——附近的像素密切相关,通常代表一些语义概念,例如轮子或窗口。这是通过使用相对较大的过滤器来利用的,过滤器可以捕获局部空间邻域中的图像特征。
- 组合性(或层次结构)——图像中较大的区域通常是它包含的较小区域的语义父级。例如,汽车是门、窗、轮子、驾驶员等的父级。而驾驶员是头部、手臂等的父级。通过堆叠卷积层和应用池化隐含地利用了这一点。
其次,卷积层中可训练参数(即滤波器)的数量不依赖于输入维度,因此从技术上讲,我们可以在 28×28 和 512×512 图像上训练完全相同的模型。换句话说,模型是参数化的。
理想情况下,我们的目标是开发一个与图神经网络一样灵活并且可以从任何数据中消化和学习的模型,但同时我们希望通过打开/关闭某些先验来控制(正则化)这种灵活性的因素。
所有这些良好的特性使 ConvNets 不太容易过度拟合(训练集精度高,验证/测试集精度低),在不同的视觉任务中更准确,并且可以轻松扩展到大型图像和数据集。因此,当我们想要解决输入数据为图结构的重要任务时,将所有这些属性转移到**图神经网络 (GNN)**以规范其灵活性并使其可扩展是很有吸引力的。理想情况下,我们的目标是开发一个与 GNN 一样灵活并且可以从任何数据中消化和学习的模型,但同时我们希望通过打开/关闭某些先验来控制(正则化)这种灵活性的因素。这可以开启许多有趣方向的研究。然而,控制这种权衡是具有挑战性的。
2.2 根据图形对图像进行卷积
让我们考虑一个有N 个节点的无向图G。边E表示节点之间的无向连接。节点和边通常来自您对问题的直觉。对于图像,我们的直觉是节点是像素或超像素(一组形状怪异的像素),边缘是它们之间的空间距离。例如,左下方的 MNIST图像通常表示为 28×28 维矩阵。我们也可以将其表示为一组N =28*28=784 个像素。所以,我们的图G将有N=784 节点和边缘将具有较大值(下图中较厚的边缘)对于靠近的像素和较小的值(较薄的边缘)对于远程像素。

左侧是来自 MNIST 数据集的图像,右侧是其图形表示的示例。右侧较暗和较大的节点对应于较高的像素强度。右图的灵感来自于 ( Fey et al., CVPR, 2018 ) 中的图 5
当我们在图像上训练我们的神经网络或 ConvNets 时,我们隐式地在图上定义图像——一个规则的二维网格,如下图所示。由于这个网格对于所有训练和测试图像都是相同的并且是规则的,即网格的所有像素在所有图像中都以完全相同的方式相互连接(即具有相同数量的邻居、边缘长度等。 ),这个规则的网格图没有信息可以帮助我们区分一个图像和另一个。下面我将一些 2D 和 3D 规则网格可视化,其中节点的顺序是颜色编码的。顺便说一句,我在 Python 中使用NetworkX来做到这一点,例如G = networkx.grid_graph([4, 4]).
给定这个 4×4 规则网格,让我们简要地看看 2D 卷积是如何工作的,以了解为什么难以将此算子转移到图形上。规则网格上的过滤器具有相同的节点顺序,但现代卷积网络通常具有较小的过滤器,例如下面示例中的 3×3。这个过滤器有 9 个值:W ?, W ?,…, W ?,这是我们在训练期间使用反向传播更新的值,以最小化损失并解决下游任务。在下面的示例中,我们只是启发式地将此过滤器初始化为边缘检测器(请参阅此处的其他可能的过滤器):

常规 2D 网格上的 3×3 滤波器示例,左侧为任意权重 w,右侧为边缘检测器。
当我们执行卷积时,我们在两个方向上滑动这个过滤器:向右和向下,但没有什么能阻止我们从底角开始——重要的是滑过所有可能的位置。在每一个位置,我们计算的点积 网格上的值之间(我们代表他们作为X)和过滤器的值,w ^:X ? Wˉˉ ?+ X ? Wˉˉ ?+ … + X ? w ^?,并将结果存储在输出图像中。在我们的可视化中,我们在滑动期间更改节点的颜色以匹配网格中节点的颜色。在常规网格中,我们总是可以将过滤器的节点与网格的节点进行匹配。不幸的是,这不适用于图表,我将在下面解释。

在规则网格上进行 2 步 2D 卷积。如果我们不应用填充,总共会有 4 个步骤,所以结果将是一个 2×2 的图像。为了使生成的图像更大,我们需要应用padding。在此处查看深度学习中的卷积综合指南。
上面使用的点积是所谓的“聚合运算符”之一。从广义上讲,聚合器运算符的目标是将数据汇总为简化形式。在上面的示例中,点积将 3×3 矩阵汇总为单个值。另一个例子是 ConvNets 中的池化。请记住,诸如 max 或 sum pooling 之类的方法是置换不变的,即即使您随机打乱该区域内的所有像素,它们也会从空间区域中汇集相同的值。为了清楚起见,点积不是置换不变的,因为一般来说:X ? W ?+ X ? W ? ≠ X ? W ?+ X? W 2。
现在让我们使用我们的 MNIST 图像并说明规则网格、过滤器和卷积的含义。记住我们的图术语,这个规则的 28×28 网格将是我们的图G,所以这个网格中的每个单元都是一个节点,节点特征是一个实际的图像X,即每个节点将只有一个特征——像素强度从 0(黑色)到 1(白色)。

常规 28×28 网格(左)和该网格上的图像(右)。
接下来,我们定义一个过滤器,让它成为具有一些(几乎)任意参数的著名Gabor 过滤器。一旦我们有了一个图像和一个过滤器,我们就可以通过在该图像(在我们的例子中是数字 7)上滑动过滤器来执行卷积,并在每一步之后将点积的结果放入输出矩阵。

一个 28×28 的过滤器(左)以及这个过滤器与数字 7 的图像(右)的 2D 卷积结果。
这一切都很酷,但正如我之前提到的,当您尝试将卷积推广到图形时会变得棘手。
节点是一个集合,这个集合的任何排列都不会改变它。因此,人们应用的聚合算子应该是permutation-invariant。
正如我已经提到的,上面用于计算每一步卷积的点积对顺序很敏感。这种敏感性使我们能够学习类似于对捕获图像特征很重要的 Gabor 滤波器的边缘检测器。问题在于,在图中没有明确定义的节点顺序,除非您学会对它们进行排序,或者想出一些启发式方法,这将导致从图到图的一致(规范)顺序。简而言之,节点是一个集合,这个集合的任何排列都不会改变它。因此,人们应用的聚合算子应该是permutation-invariant。最流行的选择是平均 (GCN, Kipf & Welling, ICLR, 2017 ) 和求和 (GIN,Xu et al., ICLR, 2019 ) 的所有邻居,即总和或平均池化,然后是可训练向量W 的投影。有关其他一些聚合器,请参见Hamilton 等人,NIPS,2017。
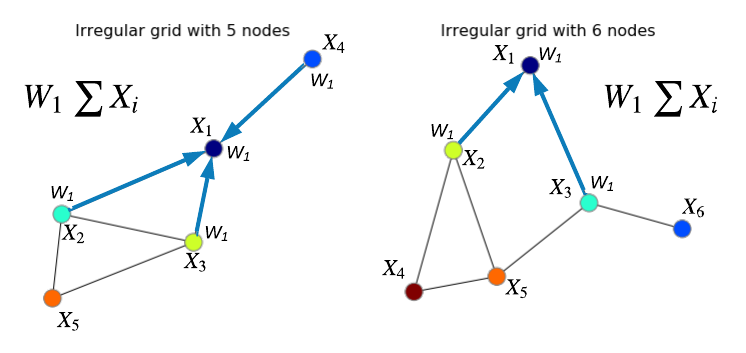
节点特征X的“图卷积”图示,过滤器W以节点 1(深蓝色)为中心。
例如,对于上图左侧的图,节点 1 的求和聚合器的输出将为X ?=( X ?+ X ?+ X ?+ X ?) W ?,对于节点 2:X ?=( X ?+ X ?+ X ?+ X ?) W ? 等用于节点 3、4 和 5,即我们需要对所有节点应用此聚合器。结果,我们将拥有具有相同结构的图,但节点特征现在将包含邻居的特征。我们可以使用相同的想法处理右边的图。
通俗地说,人们称这种平均或求和为“卷积”,因为我们也从一个节点“滑动”到另一个节点,并在每一步应用聚合器运算符。但是,重要的是要记住,这是一种非常特殊的卷积形式,其中过滤器没有方向感。下面我将展示这些过滤器的外观,并给出如何使它们更好的想法。
3 什么使神经网络成为图神经网络?
你知道经典神经网络是如何工作的,对吧?我们有一些C维特征X作为网络的输入。使用我们正在运行的 MNIST 示例,X 将是我们的C = 784 维像素特征(即“扁平化”图像)。这些特征乘以我们在训练期间更新的C × F维权重W,以使输出更接近我们的预期。结果可以直接用于解决任务(例如在回归的情况下),或者可以进一步馈送到一些非线性(激活),如 ReLU,或其他可微(或更准确地说,亚可微)函数以形成多层网络。一般来说,某层l的输出是:
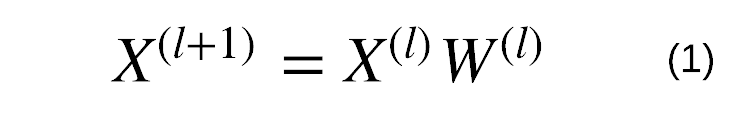
具有可学习权重 W 的全连接层。“全连接”意味着 X ???1?中的每个输出值取决于或“连接到”所有输入 X ???。通常,尽管并非总是如此,我们会在输出中添加偏置项。
MNIST 中的信号非常强,您只需使用上面的公式和交叉熵损失就可以获得 91% 的准确率,而没有任何非线性和其他技巧(我使用了一个稍微修改过的PyTorch 示例来做到这一点)。这种模型称为多项式(或多类,因为我们有 10 类数字)逻辑回归。
现在,我们如何将普通神经网络转换为图神经网络?如您所知,GNN 背后的核心思想是对“邻居”的聚合。在这里,重要的是要了解,在许多情况下,它实际上是 你 谁指定了“邻居”。
让我们先考虑一个简单的案例,当你得到一些图表时。例如,这可以是具有 5 个人的社交网络的片段(子图),并且一对节点之间的边表示两个人是否是朋友(或至少其中一个人是这样认为的)。右图中的邻接矩阵(通常表示为A)是一种以矩阵形式表示这些边的方法,方便我们的深度学习框架。矩阵中的黄色单元格代表边缘,蓝色单元格代表没有边缘。
让我们先考虑一个简单的案例,当你得到一些图表时。例如,这可以是具有 5 个人的社交网络的片段(子图),并且一对节点之间的边表示两个人是否是朋友(或至少其中一个人是这样认为的)。右图中的邻接矩阵(通常表示为A)是一种以矩阵形式表示这些边的方法,方便我们的深度学习框架。矩阵中的黄色单元格代表边缘,蓝色单元格代表没有边缘。

图及其邻接矩阵的示例。我们在两种情况下定义的节点顺序都是随机的,而图形仍然相同。
现在,让我们基于像素坐标为我们的 MNIST 示例创建一个邻接矩阵A(完整代码在帖子末尾提供):
import numpy as np
from scipy.spatial.distance import cdist
img_size = 28 # MNIST image width and height
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord) # see figure below on the left
sigma = 0.2 * np.pi # width of a Gaussian
A = np.exp(- dist ** 2 / sigma ** 2) # see figure below in the middle
这是为视觉任务定义邻接矩阵的典型方法,但不是唯一方法(Defferrard 等人,NIPS,2016 年,Bronstein 等人,2016 年)。这个邻接矩阵是我们的先验,或者我们的归纳偏差,我们根据我们的直觉强加给模型,即附近的像素应该连接而远程像素不应该或应该有非常细的边缘(小值的边缘)。这是由于观察到在自然图像中附近的像素通常对应于同一对象或频繁交互的对象(我们在第 2.1 节中提到的局部性原则),因此连接这些像素很有意义。
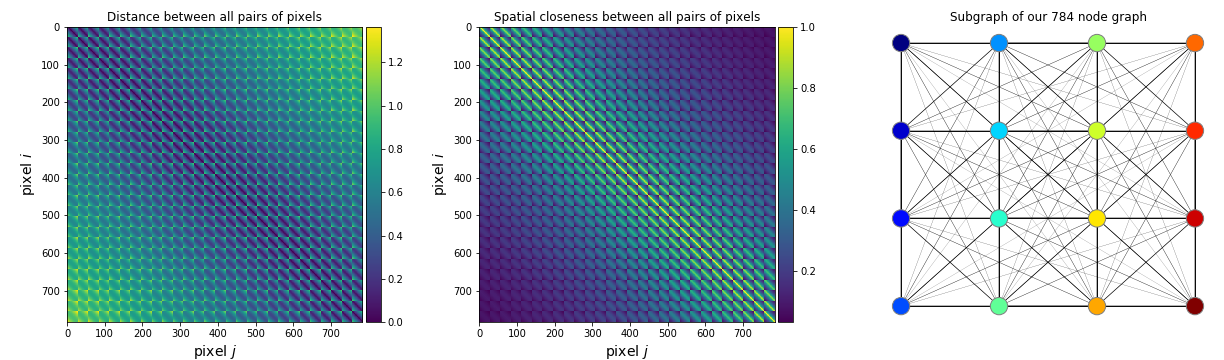
所有节点对之间的距离(左)和接近度(中)形式的邻接矩阵 ( N x N)。(右)具有 16 个相邻像素的子图,对应于中间的邻接矩阵。由于它是一个完整的子图,所以它也被称为“集团”。
所以,现在我们有一些奇特的矩阵A,其值在 [0,1] 范围内,而不是只有特征X。重要的是要注意,一旦我们知道我们的输入是一个图,我们就假设没有节点的规范顺序在数据集中的所有其他图上是一致的。就图像而言,这意味着假设像素被随机打乱。在实践中,找到节点的规范顺序是无法组合解决的。尽管对于 MNIST,我们在技术上可以通过知道这个顺序来作弊(因为数据最初来自常规网格),但它不适用于实际的图形数据集。
请记住,我们的特征矩阵X有 𝑁 行和 C 列。因此,就图而言,每一行对应一个节点,C是节点特征的维数。但是现在的问题是我们不知道节点的顺序,所以我们不知道将特定节点的特征放在哪一行。如果我们假装忽略这个问题,并像之前一样直接将X 输入到 MLP,效果将与使用随机混洗的像素输入图像相同,每个图像的独立(但每个时期都相同)混洗!令人惊讶的是,神经网络原则上仍然可以拟合这样的随机数据(Zhang et al., ICLR, 2017),但是测试性能将接近随机预测。一种解决方案是简单地使用我们之前创建的邻接矩阵A,如下所示:
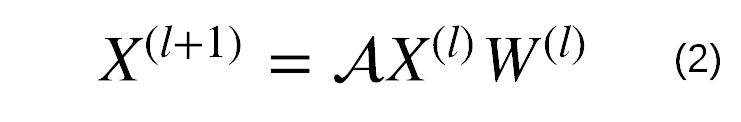
我们只需要确保该行我在一个对应于节点的功能,在排我的X。在这里,我使用 𝓐 而不是普通的A,因为通常你想要标准化A。如果 𝓐= A,矩阵乘法 𝓐 X???将等价于对邻居的特征求和,结果证明这在许多任务中都很有用(Xu et al., ICLR, 2019)。最常见的是,您对其进行标准化,以便 𝓐 X???平均邻居的特征,即 𝓐= A / Σ? A ?。正常化矩阵一种更好的方式一中可以找到(基普夫和威灵,ICLR,2017 年)。
import torch
import torch.nn as nn
C = 2 # Input feature dimensionality
F = 8 # Output feature dimensionality
W = nn.Linear(in_features=C, out_features=F) # Trainable weights
# Fully connected layer
X = torch.randn(1, C) # Input features
Z = W(X) # Output features : torch.Size([1, 8])
#Graph Neural Network layer
N = 6 # Number of nodes in a graph
X = torch.randn(N, C) # Input feature
A = torch.rand(N, N) # Adjacency matrix (edges of a graph)
Z = W(torch.mm(A, X)) # Output features: torch.Size([6, 8])
而这里是全PyTorch代码训练比上面两种型号:python mnist_fc.py --model fc训练NN情况; python mnist_fc.py --model graph训练 GNN 案例。作为练习,尝试在–model graph案例中随机打乱代码中的像素(不要忘记以相同的方式打乱A)并确保它不会影响结果。这个–model fc案子是真的吗?
运行代码后,您可能会注意到分类准确率实际上是差不多的。有什么问题?图网络不应该更好地工作吗?嗯,在很多情况下,它们是。但不是在这个,因为我们添加的 𝓐 X???运算符实际上不是别的,而是一个高斯滤波器:
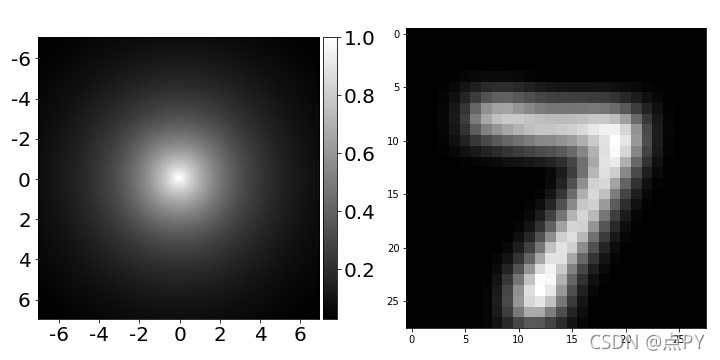
图神经网络中使用的过滤器的 2D 可视化及其对图像的影响。
因此,我们的图神经网络被证明等效于具有单个高斯滤波器的卷积神经网络,我们在训练期间从不更新,然后是全连接层。这个过滤器基本上模糊/平滑图像,这不是一个特别有用的事情(见右上方的图像)。然而,这是图神经网络的最简单的变体,但它在图结构数据上效果很好。为了让 GNN 在常规图上更好地工作,比如图像,我们需要应用一些技巧。例如,我们可以不使用预定义的高斯滤波器,而是使用如下所示的可微函数来学习预测任何像素对之间的边缘:
import torch.nn as nn # using PyTorch
nn.Sequential(nn.Linear(4, 64), # map coordinates to a hidden layer
nn.ReLU(), # nonlinearity
nn.Linear(64, 1), # map hidden representation to edge
nn.Tanh()) # squash edge values to [-1, 1]
为了让 GNN 在常规图上更好地工作,比如图像,我们需要应用一些技巧。例如,我们可以学习预测任何一对像素之间的边缘,而不是使用预定义的高斯滤波器。

生成这些 GIF 的代码非常简单:
import imageio # to save GIFs
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import cdist
import cv2 # optional (for resizing the filter to look better)
img_size = 28
# Create/load some adjacency matrix A (for example, based on coordinates)
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord) # distances between all pairs of pixels
sigma = 0.2 * np.pi # width of a Gaussian (can be a hyperparameter when training a model)
A = np.exp(- dist / sigma ** 2) # adjacency matrix of spatial similarity
# above, dist should have been squared to make it a Gaussian (forgot to do that)
scale = 4
img_list = []
cmap = mpl.cm.get_cmap('viridis')
for i in np.arange(0, img_size, 4): # for every row with step 4
for j in np.arange(0, img_size, 4): # for every col with step 4
k = i*img_size + j
img = A[k, :].reshape(img_size, img_size)
img = (img - img.min()) / (img.max() - img.min())
img = cmap(img)
img[i, j] = np.array([1., 0, 0, 0]) # add the red dot
img = cv2.resize(img, (img_size*scale, img_size*scale))
img_list.append((img * 255).astype(np.uint8))
imageio.mimsave('filter.gif', img_list, format='GIF', duration=0.2)
4 结论
图神经网络是一个非常灵活和有趣的神经网络家族,可以应用于真正复杂的数据。与往常一样,这种灵活性必须付出一定的代价。在 GNN 的情况下,很难通过将此类运算符定义为卷积来规范模型。这个方向的研究进展非常快,因此 GNN 将在机器学习和计算机视觉领域越来越广泛的领域得到应用。
参考
https://medium.com/@BorisAKnyazev/tutorial-on-graph-neural-networks-for-computer-vision-and-beyond-part-1-3d9fada3b80d