机器学习之乳腺癌预测
(一)问题分析
1.问题背景
乳腺癌是女性最常见的恶性肿瘤，占美国女性确诊癌症的近三分之一，是女性癌症死亡的第二大原因。 乳腺癌是乳房组织细胞异常生长的结果，通常称为肿瘤。 肿瘤并不意味着癌症——肿瘤可以是良性（非癌性）、恶性前（癌前）或恶性（癌性）。 MRI、乳房X光检查、超声波和活组织检查等测试通常用于诊断所进行的乳腺癌。
2.问题分析
原理：乳房细针抽吸 (FNA) 测试鉴定乳腺癌（这是一种快速且简单的程序，该程序可以从乳房病变或囊肿（肿块、溃疡或肿胀）中取出一些液体或细胞，用类似于 血样针）。
通过检测数据和标签构建模型，实现对乳腺癌肿瘤进行分类：
1 = 恶性 (癌性)
0 = 良性 (非癌性)
很明显，这是一个二分类问题。
3.题目所需的代码及数据
链接：https://pan.baidu.com/s/1bS7Ku_PUfcimiVkmLz9Fzw
提取码：0929
(二).导入数据
1. 认识数据集
数据集中的前两列分别存储样本的唯一 ID 号和相应的诊断（M=恶性，B=良性）。
第 3-32 列包含 30 个实值特征，这些特征是根据细胞核的数字化图像计算得出的，可用于构建模型来预测肿瘤是良性还是恶性。
为每个细胞核计算十个实值特征：
a) 半径（从中心到周边点的平均距离）
b) 纹理（灰度值的标准偏差）
c) 周长
d) 面积
e) 平滑度（半径长度的局部变化）
f) 紧凑性（周长^2/面积 - 1.0）
g) 凹度（轮廓凹入部分的严重程度）
h) 凹点（轮廓凹入部分的数量）
i) 对称性
j) 分形维数（“海岸线近似” - 1）
2.导入数据
#load libraries
import matplotlib.pyplot
import matplotlib.pyplot as plt
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
data = pd.read_csv('data/data.csv', index_col=False,)
print("输出一下数据的行列数：",end="")
print(data.shape)
print("输出一下数据的信息：")
data.info()
data.dtypes.value_counts
#检查缺少的变量
data.isnull().any()
data.diagnosis.unique()
print("将修改过后的数据保存到新csv文件中(保存dataframe的更新版本以备将来分析)")
data.to_csv('data/clean-data.csv')
# 查看数据前两行
print(data.head(2))
# 对标签进行统计
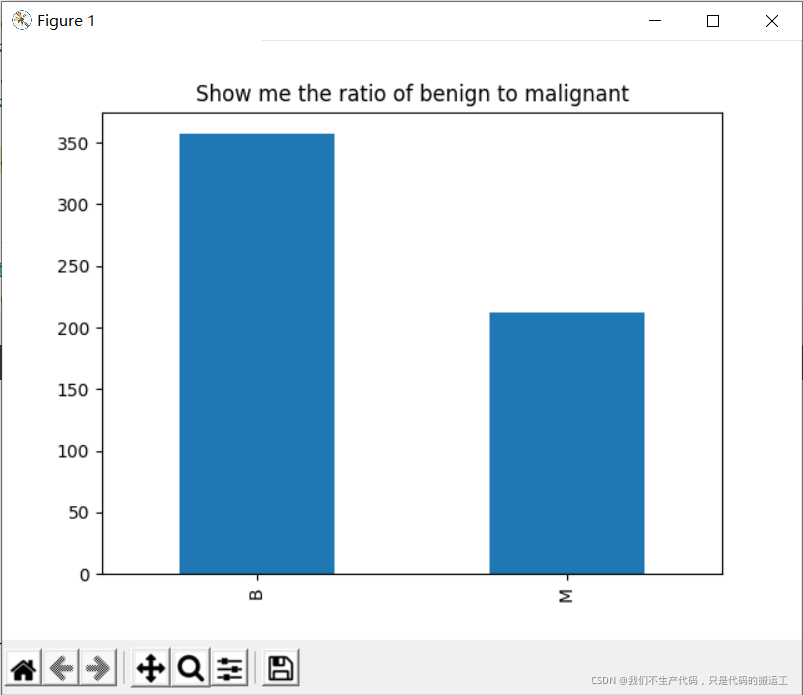
#良性：恶性 大约为2：1. 在机器学习中最好是正负样本1：1，但是2：1也可以进行正常的分类预测。
data.diagnosis.value_counts().plot(kind = "bar")
plt.title("Show me the ratio of benign to malignant")
matplotlib.pyplot.show()
3.数据概述
总共30个特征，分别是对10个实值特征计算，mean, se, worst
diagnosis 列为标签
数据无空值
(三)EDA 数据探索性分析
探索性数据分析（EDA）是一个非常重要的步骤，应该在任何建模之前完成。这是因为数据科学家能够在不做假设的情况下理解数据的性质。数据探索主要是掌握，数据的结构，值的分布，在数据集中是否存在异常值，特征间相互关系。
主要包括：
描述性统计分析
数据可视化
1.描述性统计分析
A.查看数据维度(行列数)
输出一下数据的行列数：(569, 32)
B.数据统计描述(列名对应的信息)
输出一下数据的信息：
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 569 entries, 0 to 568
Data columns (total 32 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 id 569 non-null int64
1 diagnosis 569 non-null object
2 radius_mean 569 non-null float64
3 texture_mean 569 non-null float64
4 perimeter_mean 569 non-null float64
5 area_mean 569 non-null float64
6 smoothness_mean 569 non-null float64
7 compactness_mean 569 non-null float64
8 concavity_mean 569 non-null float64
9 concave points_mean 569 non-null float64
10 symmetry_mean 569 non-null float64
11 fractal_dimension_mean 569 non-null float64
12 radius_se 569 non-null float64
13 texture_se 569 non-null float64
14 perimeter_se 569 non-null float64
15 area_se 569 non-null float64
16 smoothness_se 569 non-null float64
17 compactness_se 569 non-null float64
18 concavity_se 569 non-null float64
19 concave points_se 569 non-null float64
20 symmetry_se 569 non-null float64
21 fractal_dimension_se 569 non-null float64
22 radius_worst 569 non-null float64
23 texture_worst 569 non-null float64
24 perimeter_worst 569 non-null float64
25 area_worst 569 non-null float64
26 smoothness_worst 569 non-null float64
27 compactness_worst 569 non-null float64
28 concavity_worst 569 non-null float64
29 concave points_worst 569 non-null float64
30 symmetry_worst 569 non-null float64
31 fractal_dimension_worst 569 non-null float64
dtypes: float64(30), int64(1), object(1)
C.查看数据信息(统计学信息)
输出一下对数据的统计描述：
radius_mean texture_mean ... symmetry_worst fractal_dimension_worst
count 569.000000 569.000000 ... 569.000000 569.000000
mean 14.127292 19.289649 ... 0.290076 0.083946
std 3.524049 4.301036 ... 0.061867 0.018061
min 6.981000 9.710000 ... 0.156500 0.055040
25% 11.700000 16.170000 ... 0.250400 0.071460
50% 13.370000 18.840000 ... 0.282200 0.080040
75% 15.780000 21.800000 ... 0.317900 0.092080
max 28.110000 39.280000 ... 0.663800 0.207500
[8 rows x 30 columns]
D.缺失处理
#检查缺少的变量
data.isnull().any()
data.diagnosis.unique()
2.数据可视化
A.数据分布情况
良性：恶性 大约为2：1. 在机器学习中最好是正负样本1：1，但是2：1也可以进行正常的分类预测。
数据可视化——直方图
各组特征可视化 – 直方图
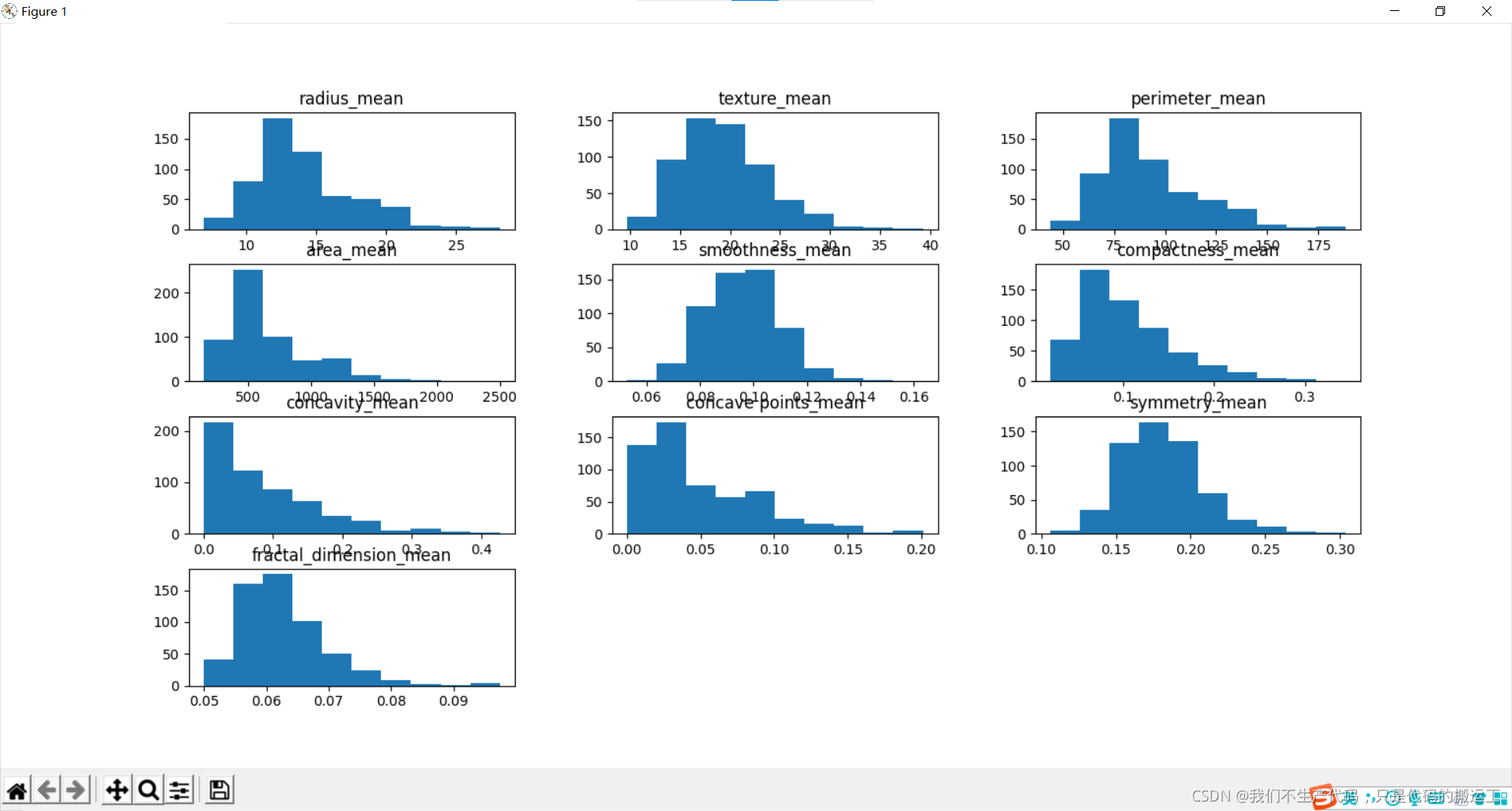
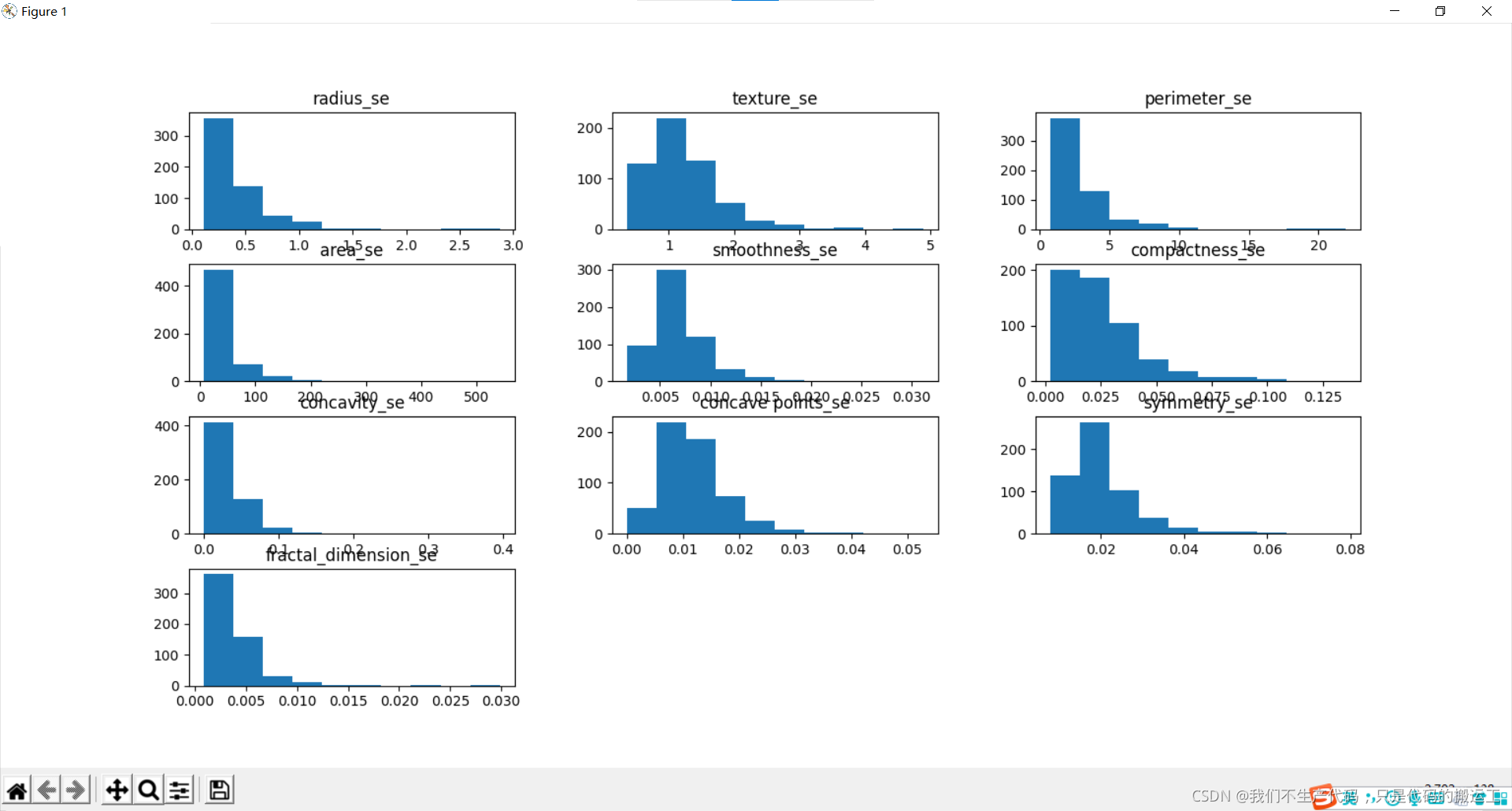
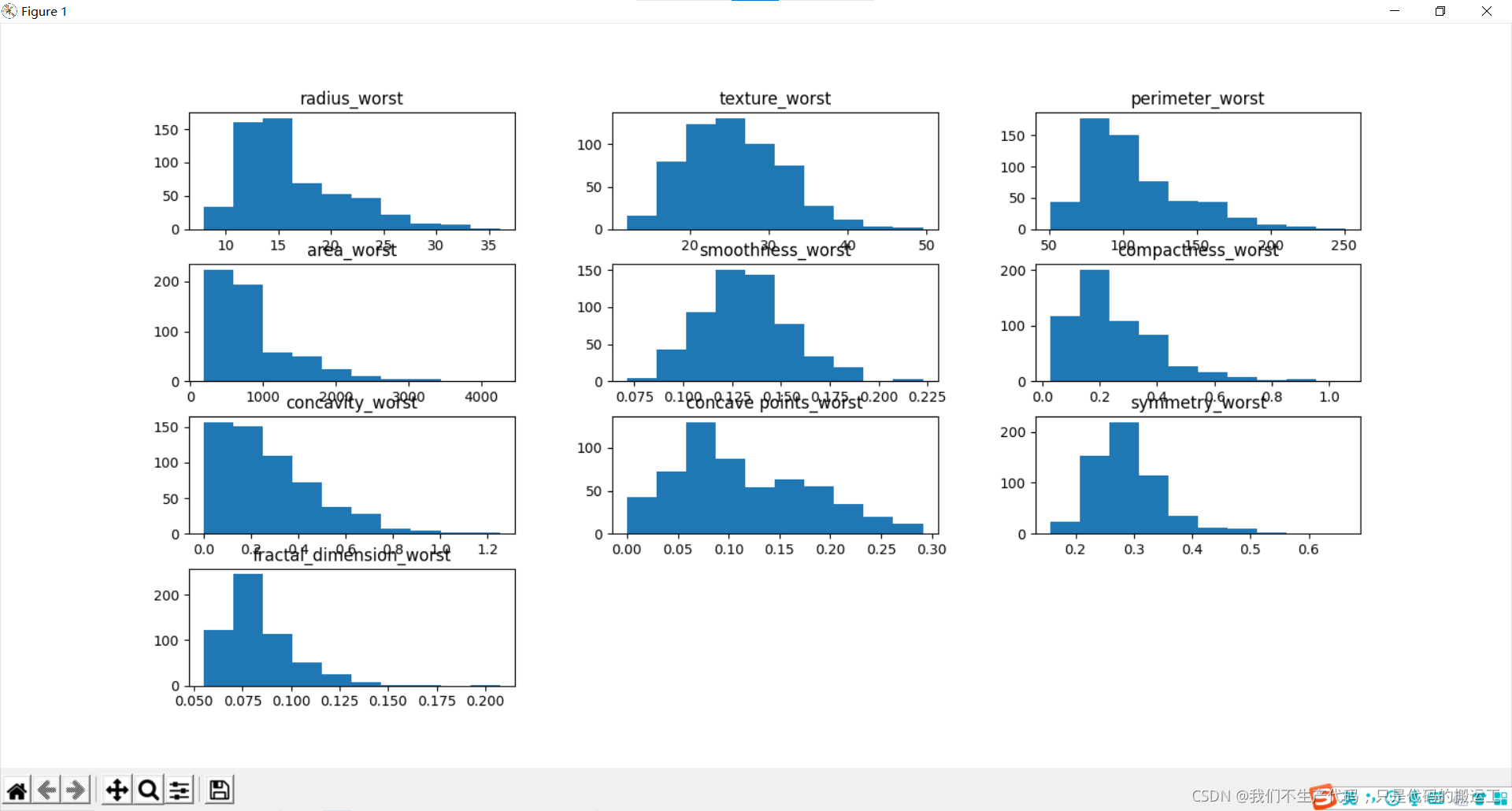我们可以看到，也许属性 凹度， 凹点 可能具有指数分布。 我们还可以看到，纹理，平滑，对称属性可能具有高斯或接近高斯分布。许多机器学习技术假设输入变量的高斯单变量分布。
数据可视化——概率密度图
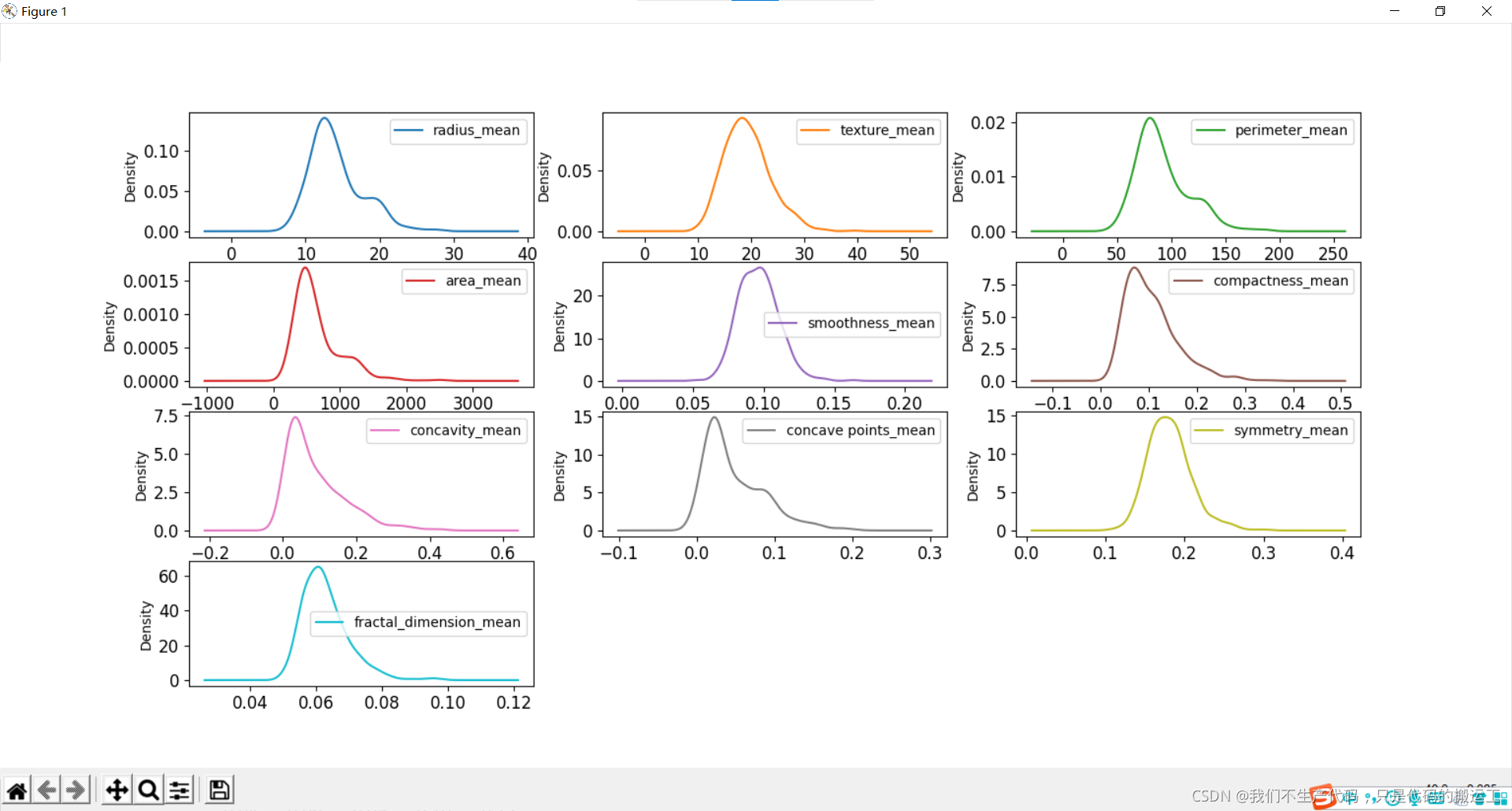
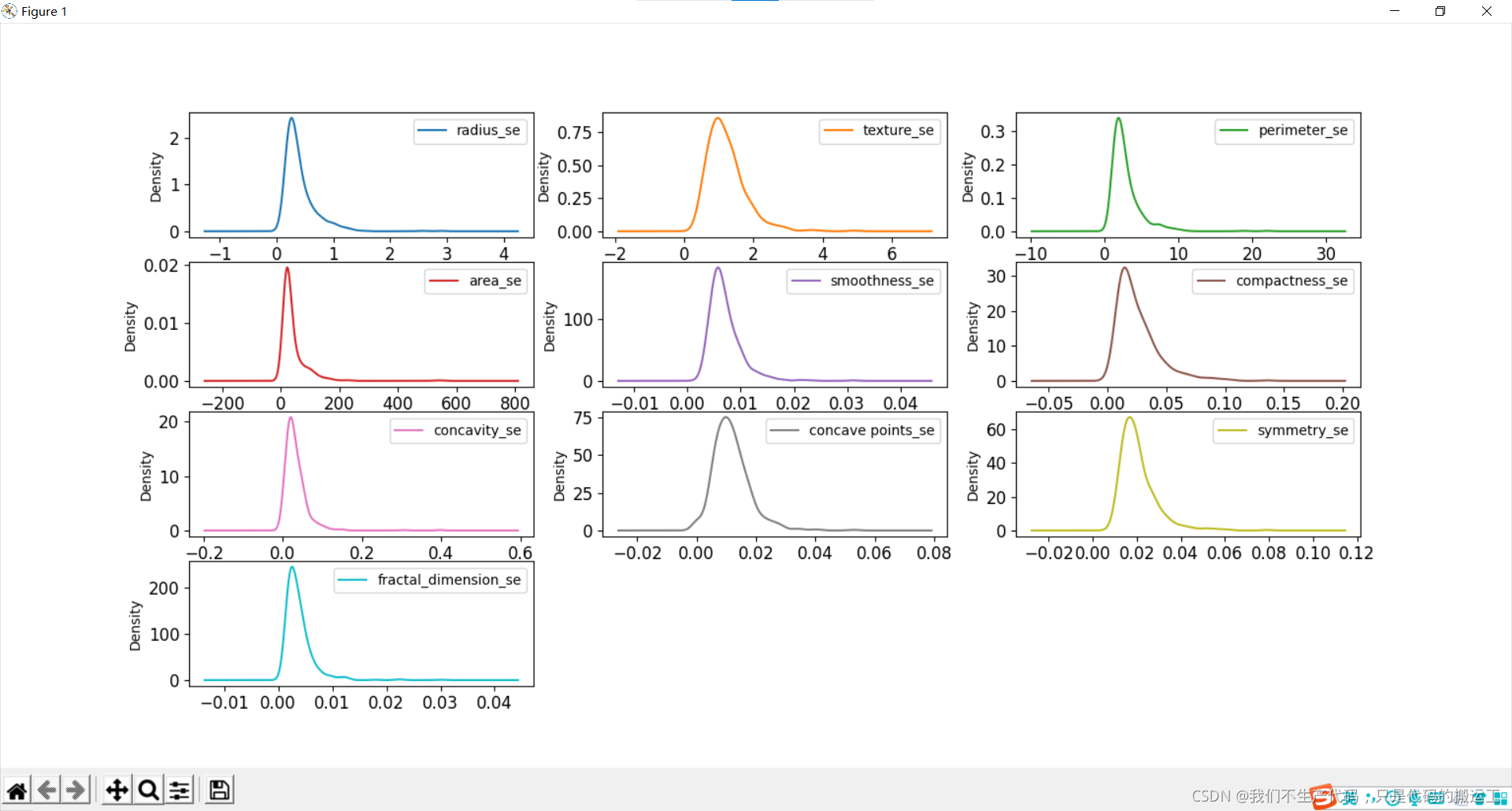
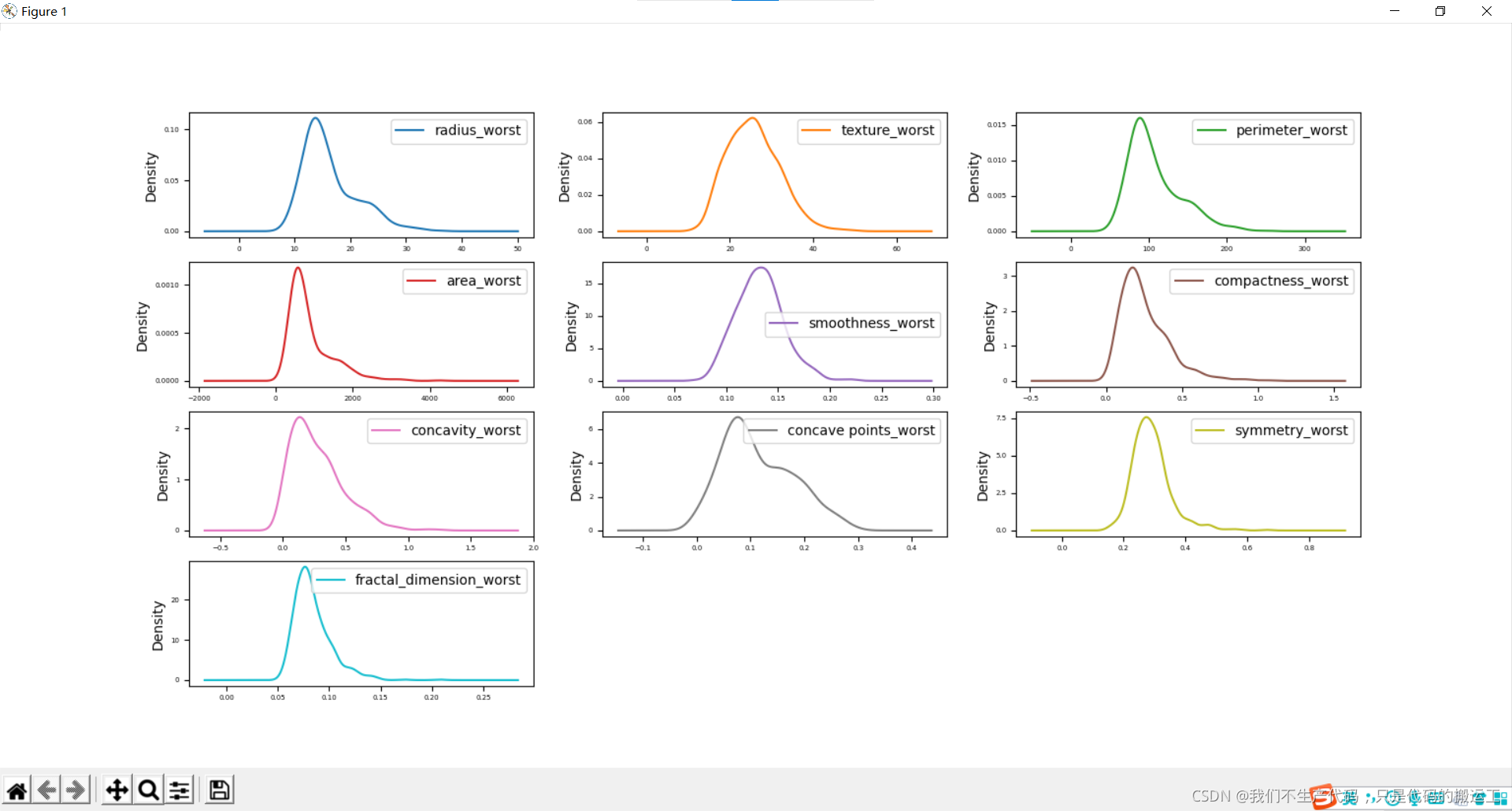周长、半径、面积、凹度、密度可能具有指数分布； 纹理、平滑、对称属性可能具有高斯或接近高斯分布。
中心极限定理告诉我们当样本数趋向于无穷大时，样本的分布会接近正态分布，但有些变量本身的分布就不是正态的，那么对于一些有正态假设的检验，估计的模型来说，就需要事先对变量做分布变换
另一方面极大或极小的值经过变换后跟正常值差距缩小，减少了极值对模型的扰动
数据可视化——箱线图
通过箱线图可视化数据分布情况和异常值
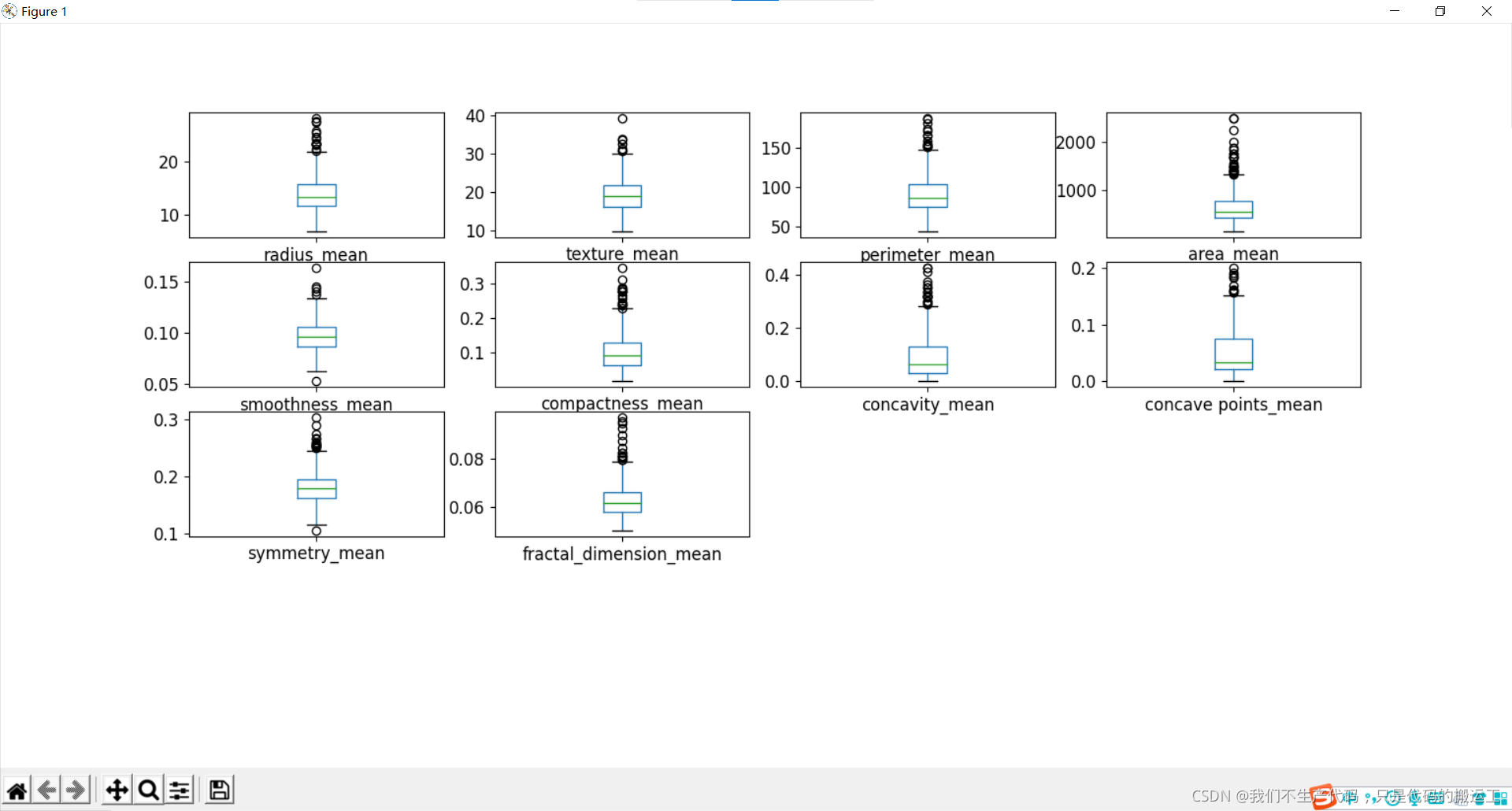
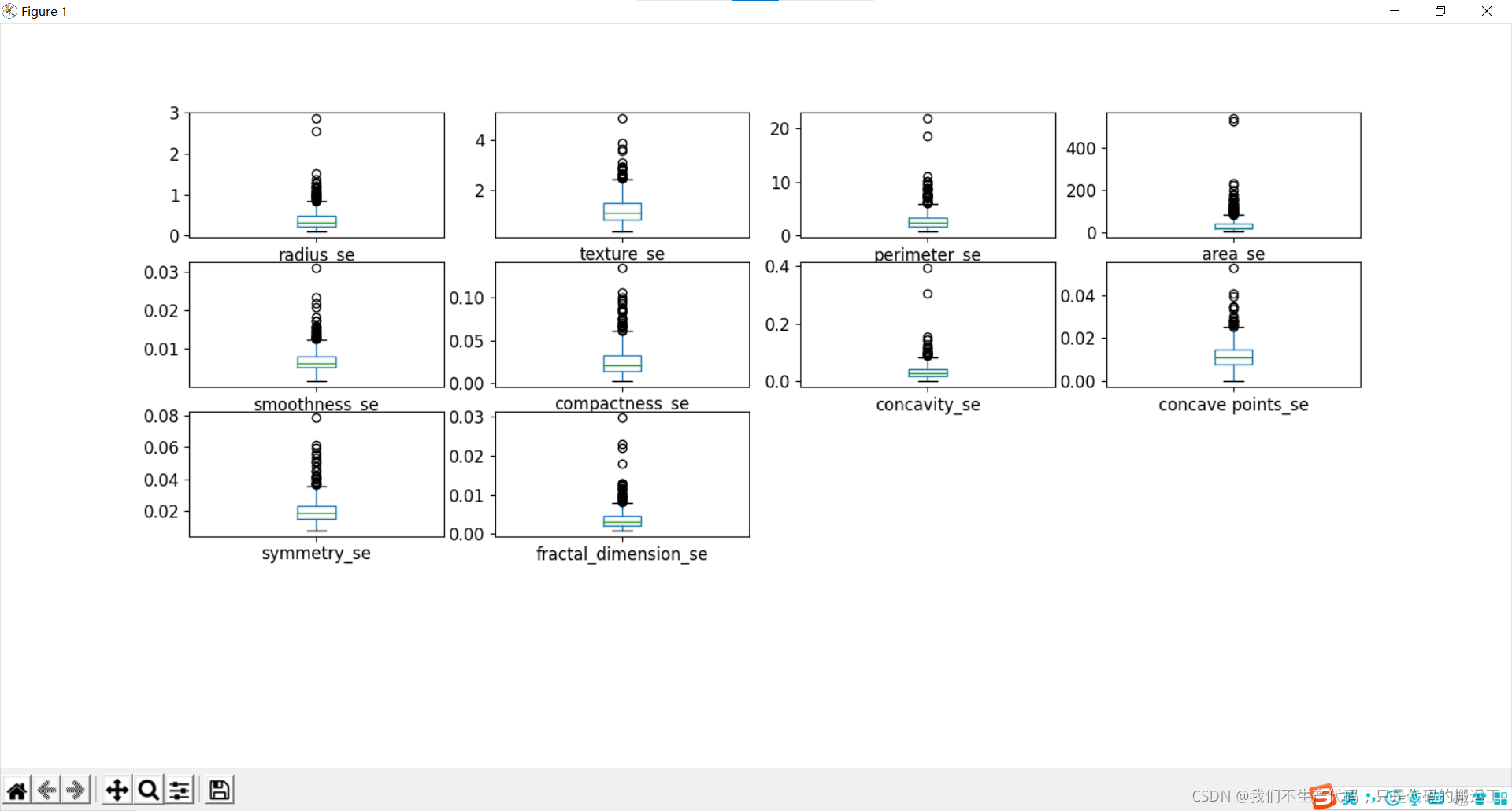
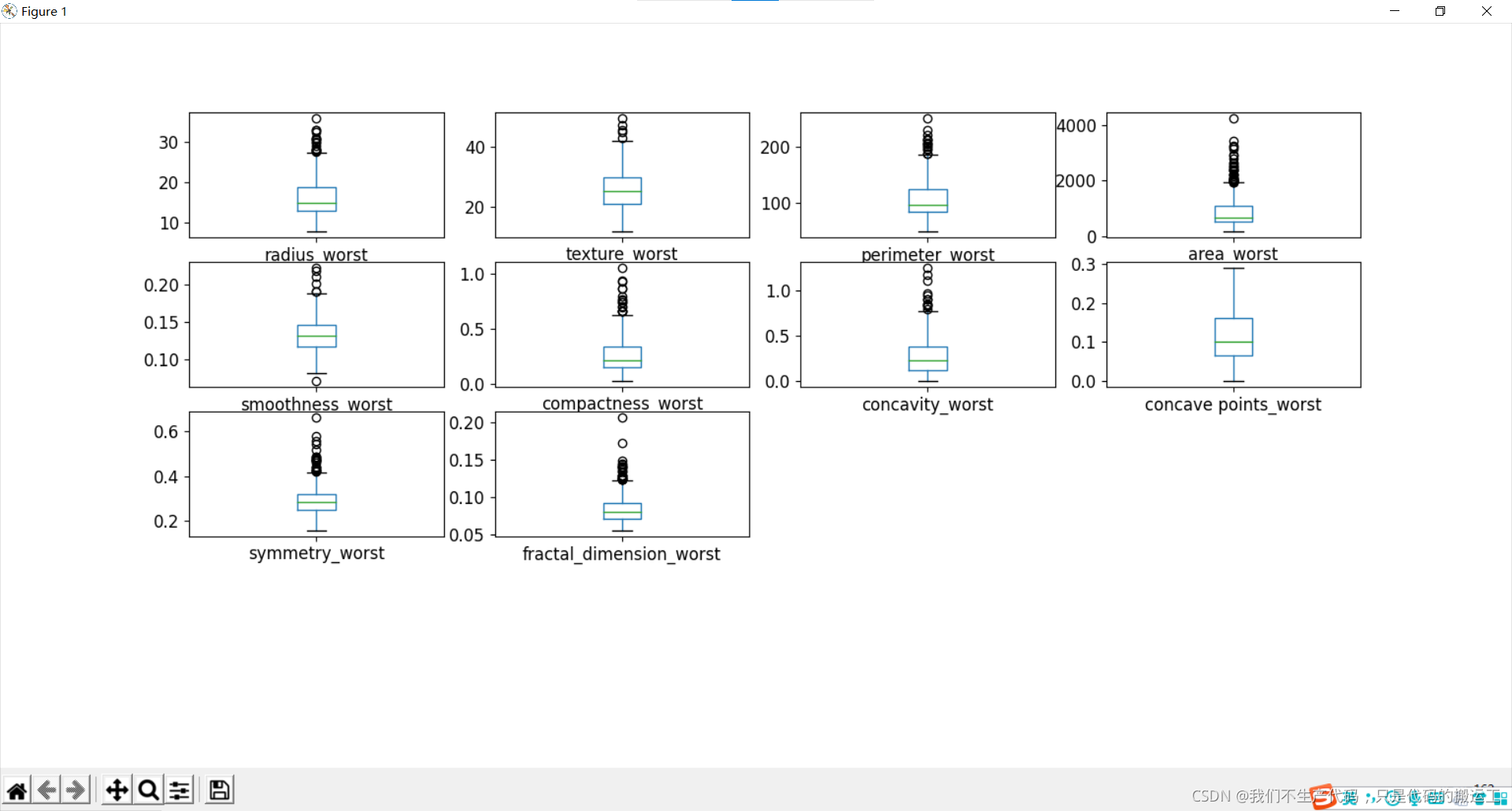
小结：
细胞半径、周长、面积、紧密度、凹度和凹点的平均值可用于癌症的分类。 这些参数的较大值倾向于显示与恶性肿瘤的相关性。
质地、平滑度、对称性或分维数的平均值并未显示出较好的诊断偏好。
在任何直方图中，都没有明显的异常值需要进一步清理
(四).预处理与特征工程
1.划分数据集
print("划分数据集")
#Assign predictors to a variable of ndarray (matrix) type
X = data.iloc[:,2:32]#从第二列到第32列
y = data.iloc[:,1].apply(lambda x: 1 if x == "M" else 0)#第一列的数据
##Split data set in train 70% and test 30%
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=7)
#其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)
2.数据标准化处理
print("数据标准化(标准化数据（以0为中心并缩放以消除差异）)")
scaler =StandardScaler()
Xs = scaler.fit_transform(X)
print(Xs)
3.PCA降维
print("PCA降维(降维处理之后的数据)")
# 从 30维 降到 10维
pca = PCA(n_components=10)
fit = pca.fit(Xs)
X_pca = pca.transform(Xs)
PCA_df = pd.DataFrame()
PCA_df['PCA_1'] = X_pca[:,0]
PCA_df['PCA_2'] = X_pca[:,1]
print(PCA_df['PCA_1'] )
print(PCA_df['PCA_2'] )
## 可视化
plt.figure(figsize=(10,6))
#画一下降维后的恶性 良性的图
plt.plot(PCA_df['PCA_1'][data.diagnosis == 'M'],
PCA_df['PCA_2'][data.diagnosis == 'M'],
'o', alpha = 0.7, color = 'r')
plt.plot(PCA_df['PCA_1'][data.diagnosis == 'B'],
PCA_df['PCA_2'][data.diagnosis == 'B'],
'o', alpha = 0.7, color = 'b')
plt.xlabel('PCA_1')
plt.ylabel('PCA_2')
plt.title("View the discrimination of features after dimensionality reduction")
plt.legend(['Malignant','Benign'])
plt.show()
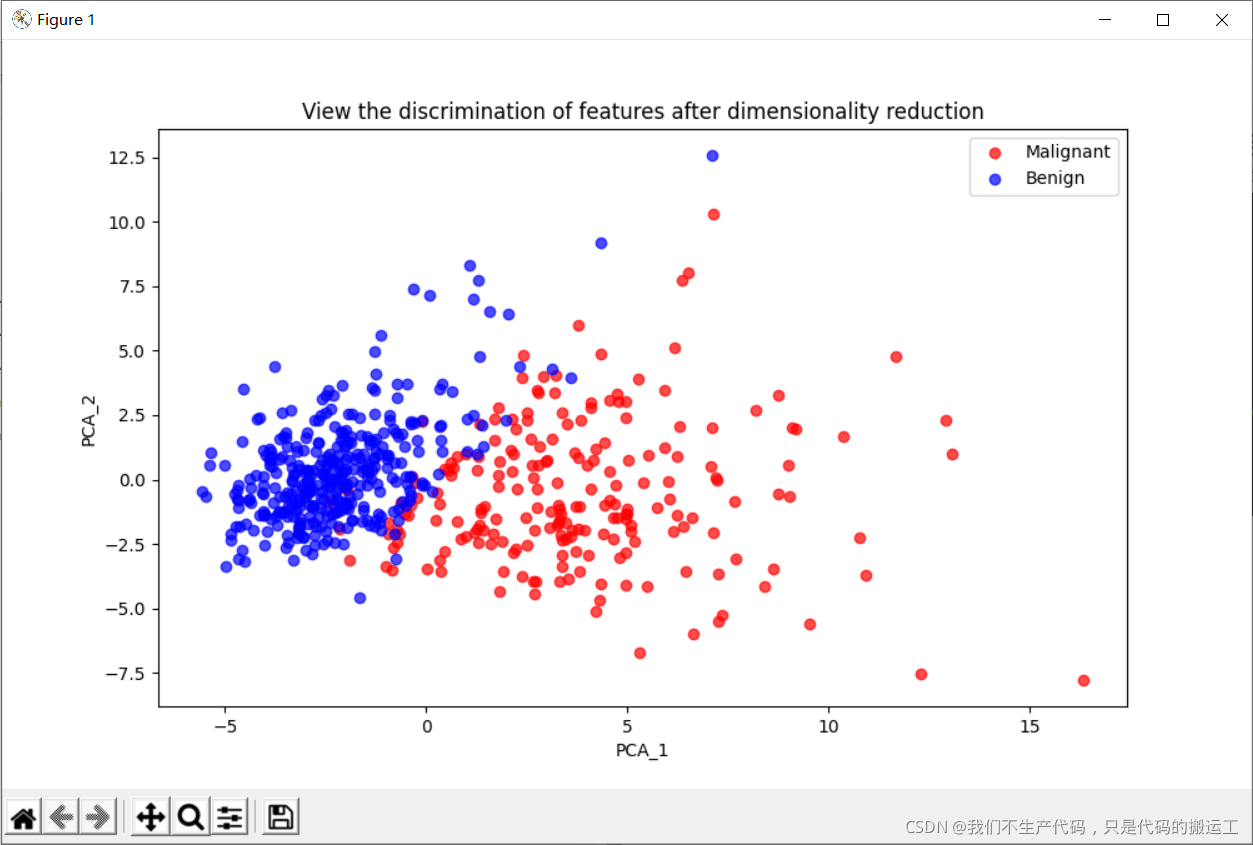
4. 画一下降维后的恶性 良性的图
#画一下降维后的恶性 良性的图
plt.plot(PCA_df['PCA_1'][data.diagnosis == 'M'],
PCA_df['PCA_2'][data.diagnosis == 'M'],
'o', alpha = 0.7, color = 'r')
plt.plot(PCA_df['PCA_1'][data.diagnosis == 'B'],
PCA_df['PCA_2'][data.diagnosis == 'B'],
'o', alpha = 0.7, color = 'b')
plt.xlabel('PCA_1')
plt.ylabel('PCA_2')
plt.title("View the discrimination of features after dimensionality reduction")
plt.legend(['Malignant','Benign'])
plt.show()
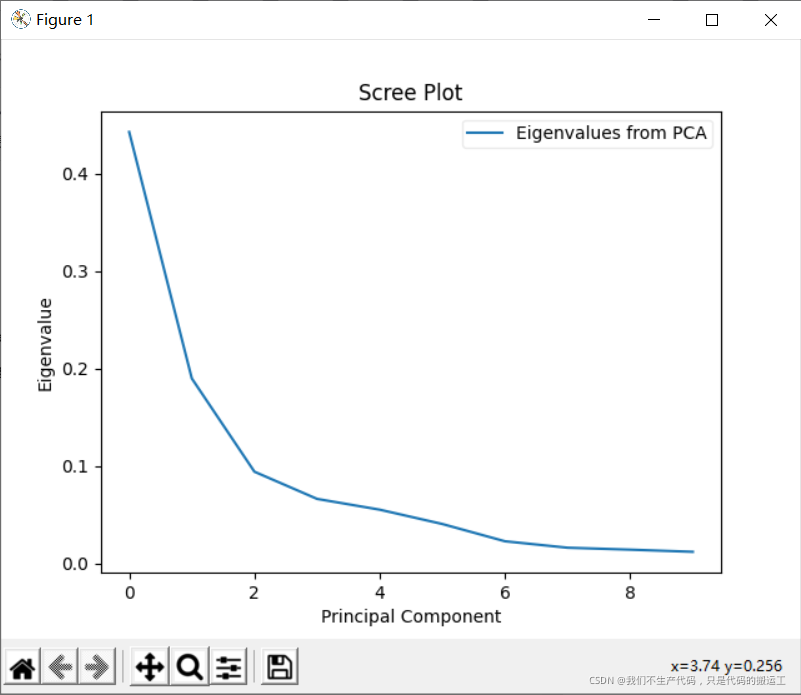
#每个PC解释的差异量
var = pca.explained_variance_ratio_
### 通过拐点确定选择前几个PC
plt.plot(var)
plt.title('Scree Plot')
plt.xlabel('Principal Component')
plt.ylabel('Eigenvalue')
#写一下标签的内容
leg = plt.legend(['Eigenvalues from PCA'],
loc='best',
borderpad=0.3,
shadow=False,
markerscale=0.4)
leg.get_frame().set_alpha(0.4)
leg.set_draggable(state=True)
plt.show()
(五).不同模型之间的比较
1.读入数据，训练集测试集划分(使用了交叉验证)
data = pd.read_csv('data/data.csv')
print("数据预处理：")
# 划分一下特征和标签
X = data.iloc[:,2:32] # 特征
y = data.iloc[:,1] # 标签
# 将类标签从其原始字符串表示（M和B）转换为整数
le = LabelEncoder()
y = le.fit_transform(y)
print(y)
# 标准化数据（以0为中心并缩放以消除差异）。
scaler =StandardScaler()
Xs = scaler.fit_transform(X)
print("交叉验证：(交叉验证训练集：测试集 = 7：3)")
# 5.划分测试集和训练集
#stratify是为了保持split前类的分布
#将stratify=X就是按照X中的比例分配
#将stratify=y就是按照y中的比例分配
X_train, X_test, y_train, y_test = train_test_split(Xs, y, stratify=y,#Xs是特征 y是标签
test_size=0.3,
random_state=33)
2.调用多种模型进行预测
# 算法审查
models = {}
models['LR'] = LogisticRegression()
models['LDA'] = LinearDiscriminantAnalysis()
models['KNN'] = KNeighborsClassifier()
models['CART'] = DecisionTreeClassifier()
models['NB'] = GaussianNB()
models['SVM'] = SVC()
num_folds = 10
seed = 7
kfold = KFold(n_splits=num_folds, shuffle=True, random_state=seed)
#kf = KFold(n_splits=7, shuffle=True, random_state=0)
# 评估算法
results = []
for name in models:
result = cross_val_score(models[name], X_train, y_train, cv=kfold, scoring='accuracy')
results.append(result)
msg = '%s: %.3f (%.3f)' % (name, result.mean(), result.std())
print(msg)
# 图表显示
fig = plt.figure()
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(models.keys())
plt.show()
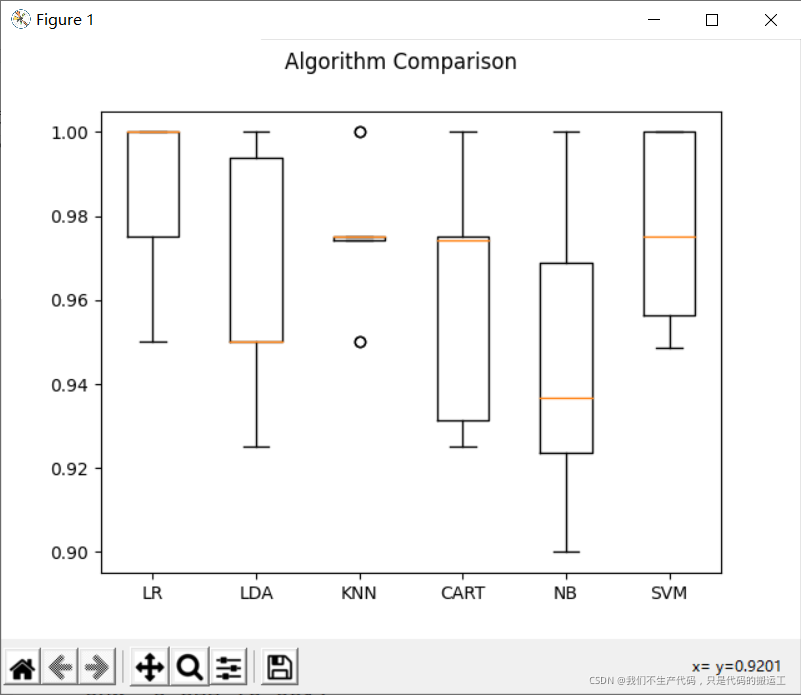
可以发现，CART(决策树分类算法)对与数据的是否标准化无影响
LDA(线性判别分析),NB(贝叶斯分类算法) 算法 有轻微影响
LR(逻辑回归算法), KNN(最近邻分类算法),SVM(支持向量机算法) 在进行建模之前，必须要进行合理的数据标准化，因为这对于模型训练有很大的影响.