详情参考:(16条消息) 李宏毅2020机器学习课程笔记(一)_?-CSDN博客
https://andyguo.blog.csdn.net/article/list/4
1.机器学习概念:
- 定义模型集合/函数集合。
- 定义损失函数(LOSS)来评价模型/函数好坏。
- 最佳函数
梯度下降(Gradient Descent ):
回归问题的损失函数是凸函数(convex),意味着一定会找到全局最优解。但是,其它的机器学习问题中,多个参数的梯度下降可能会陷入局部最优解。
过拟合、欠拟合的问题及解决方法:
过拟合时,使用正则化。
正则化的作用是降低模型的泛化误差。
回归问题的机器学习三步骤:
1.定义模型集合:f=w?x+b
2.定义损失函数(LOSS)来评价模型好坏
3.选择最佳模型
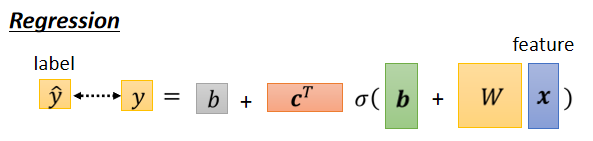
?

?

?
?2.偏差(bias)和方差
(详情参考)
【李宏毅机器学习CP5-8】(task3上)误差分析+梯度下降优化_明确目标,勿欺骗自己,小白冲冲冲-CSDN博客
偏差:平均模型(对用所有训练集得到的所有模型求平均值)与真实模型之间的差距
方差:用所有训练集得到的所有模型本身也各不相同,他们的变动水平即方差
首先 Error = Bias + VarianceError反映的是整个模型的准确度,Bias反映的是模型在样本上的输出与真实值之间的误差,即模型本身的精准度,Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性
(举一个例子,一次打靶实验,目标是为了打到10环,但是实际上只打到了7环,那么这里面的Error就是3。具体分析打到7环的原因,可能有两方面:一是瞄准出了问题,比如实际上射击瞄准的是9环而不是10环;二是枪本身的稳定性有问题,虽然瞄准的是9环,但是只打到了7环。那么在上面一次射击实验中,Bias就是1,反应的是模型期望与真实目标的差距,而在这次试验中,由于Variance所带来的误差就是2,即虽然瞄准的是9环,但由于本身模型缺乏稳定性,造成了实际结果与模型期望之间的差距)
?
1)评估x的偏差bias
假设 x? 的平均值是 μ ,方差为?
评估平均值要怎么做呢?
?
?2)评估x的方差variable
3)方差VS偏差
欠拟合(underfitting):误差来源于bias——模型不能很好地拟合训练数据
过拟合(overfitting):误差来源于variance——模型拟合了训练数据,但在测试数据上有很大误差。
三.训练集(鞍点,驻点)
?注1:将训练数据分为测试集和验证集。
做实验、发表论文时所谓的测试集,实际上是一个public testing set,而真正的测试集是一个private testing set,是一个谁也不知道的东西(我们不知道后人会输入什么数据到模型中),因此,我们不应该以public testing set作为选择模型的标准,而是应该以validation的结果来选择最好的模型。
注2:用validation选好模型后,可以把测试集和验证集一起作为训练数据,再对模型进行一次训练。但是!千万不要在看到public testing set的结果后,再想着去调整训练好的模型,这样的调整是无意义的。
Optimization with Batch
实际上在算微分的时候,并不是真的对所有 Data 算出来的 L 作微分,你是把所有的 Data 分成一个一个的 Batch
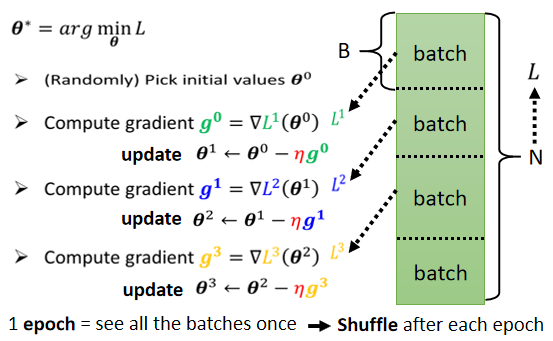
每一个 Batch 的大小呢,就是大笔的资料,我们每次在 Update 参数的时候,我们是拿大笔资料出来,算个 Loss,算个 Gradient,Update 参数,拿另外一笔资料,再算个 Loss,再算个 Gradient,再 Update 参数,以此类推,所以我们不会拿所有的资料一起去算出 Loss,我们只会拿一个 Batch 的资料,拿出来算 Loss
所有的 Batch 看过一遍,叫做一个 Epoch。
1.Small Batch v.s. Large Batch
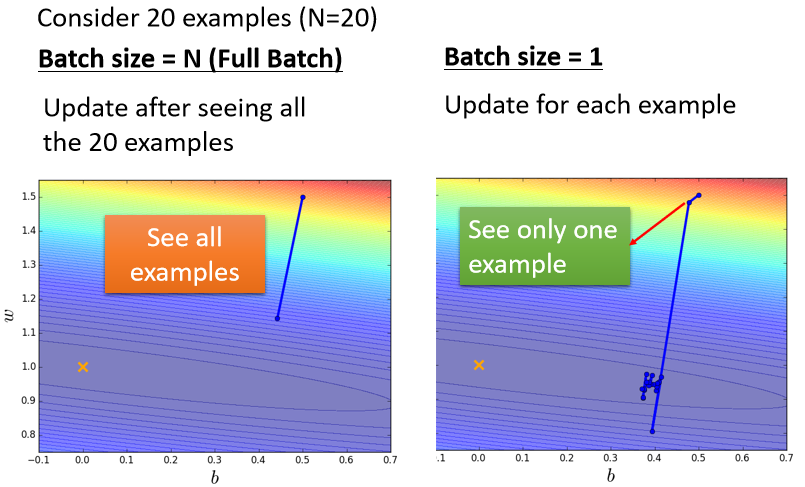
??我们来比较左右两边这两个 Case,那假设现在我们有20笔训练资料
- 左边的 Case 就是没有用 Batch,Batch Size,直接设的跟我训练资料一样多,这种状况叫做 Full Batch,就是没有用 Batch 的意思
- 那右边的 Case 就是,Batch Size 等於1
这是两个最极端的状况
先来看左边的 Case,因為没有用 Batch,我们的 Model 必须把20笔训练资料都看完,才能够计算 Loss,才能够计算 Gradient,所以我们必须要把所有20笔 Examples 都看完以后,我们的参数才能够 Update 一次
如果 Batch Size 等於1的话,代表我们只需要拿一笔资料出来算 Loss,我们就可以 Update 我们的参数,所以每次我们 Update 参数的时候,看一笔资料就好,所以我们开始的点在这边,看一笔资料 就 Update 一次参数,再看一笔资料 就 Update 一次参数,如果今天总共有20笔资料的话 那在每一个 Epoch 裡面,我们的参数会 Update 20次,因為我们现在是只看一笔资料,就 Update 一次参数,所以用一笔资料算出来的 Loss,显然是比较 Noisy 的,所以我们今天 Update 的方向,你会发现它是曲曲折折的
看起来左边的方法跟右边的方法,他们各自都有擅长跟不擅长的东西,左边是蓄力时间长,但是威力比较大,右边技能冷却时间短,但是它是比较不準的
(1)更大的batch不需要花费更多的时间计算梯度
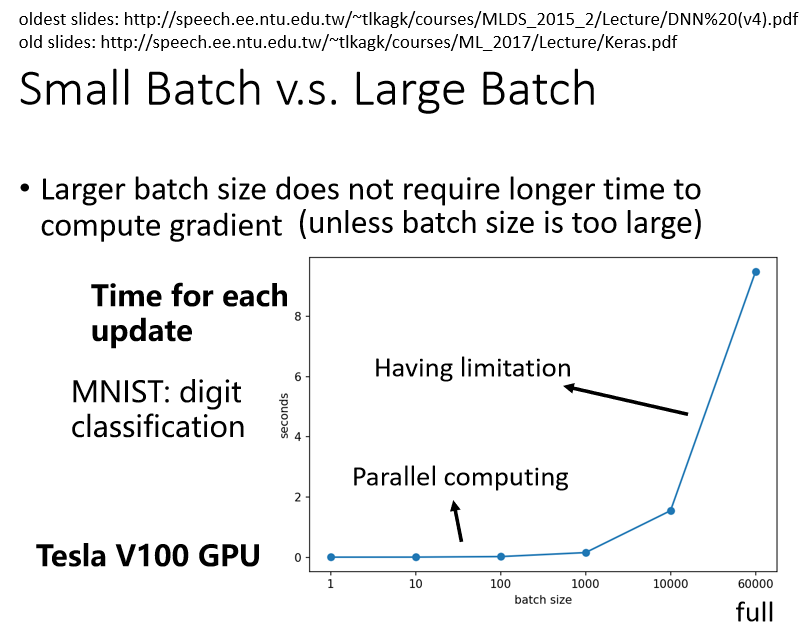
?上图列出了 Batch Size 等於1 等於10,等於100 等於1000 所需要耗费的时间
(2)Smaller batch requires longer time for one epoch
迭代iteration:更新一次参数的步骤
批量batch:一次迭代用的样本,而批量大小batch size指一个批量内的样本个数
期epoch:指整个训练集被算法遍历一次
如果今天假设我们的训练资料只有60000笔,那 Batch Size 设1,那你要60000个 Update 才能跑完一个 Epoch,如果今天是 Batch Size 等於1000,你要60个 Update 才能跑完一个 Epoch,假设今天一个 Batch Size 等於1000,要算 Gradient 的时间根本差不多,那60000次 Update,跟60次 Update 比起来,它的时间的差距量就非常可观了
?
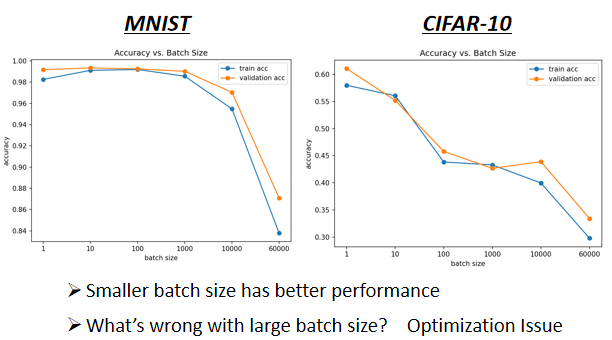
- 横轴代表的是 Batch Size,从左到右越来越大
- 纵轴代表的是正确率,越上面正确率越高,当然正确率越高越好
大的 Batch Size,往往在 Training 的时候,会给你带来比较差的结果
这个是 Optimization 的问题,代表当你用大的 Batch Size 的时候,你的 Optimization 可能会有问题,小的 Batch Size,Optimization 的结果反而是比较好的
(3)“Noisy” update is better for training
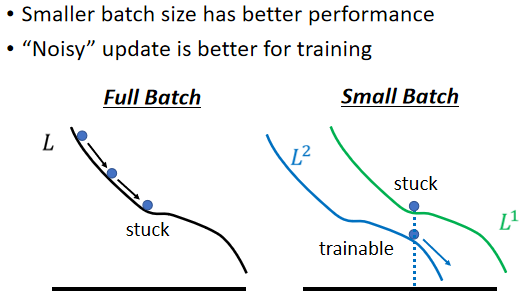
假设你是 Full Batch,那你今天在 Update 你的参数的时候,你就是沿著一个 Loss Function 来 Update 参数,今天 Update 参数的时候走到一个 Local Minima,走到一个 Saddle Point,显然就停下来了,Gradient 是零,如果你不特别去看Hession的话,那你用 Gradient Descent 的方法,你就没有办法再更新你的参数了
?
但是假如是 Small Batch 的话,因為我们每次是挑一个 Batch 出来,算它的 Loss,所以等於是,等於你每一次 Update 你的参数的时候,你用的 Loss Function 都是越有差异的,你选到第一个 Batch 的时候,你是用 L1 来算你的 Gradient,你选到第二个 Batch 的时候,你是用 L2 来算你的 Gradient,假设你用 L1 算 Gradient 的时候,发现 Gradient 是零,卡住了,但 L2 它的 Function 跟 L1 又不一样,L2 就不一定会卡住,所以 L1 卡住了 没关係,换下一个 Batch 来,L2 再算 Gradient。
?
(4)“Noisy” update is better for generalization
小的 Batch 也对 Testing 有帮助
2.Momentum
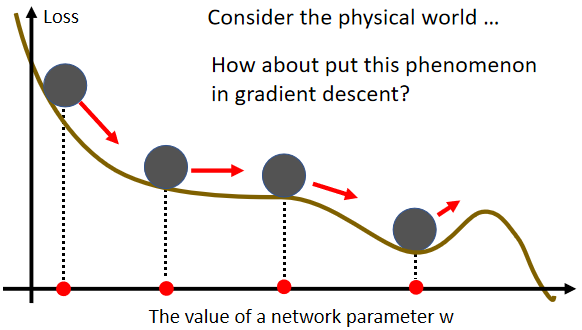
(1)Small Gradient
(2)Vanilla Gradient Descent
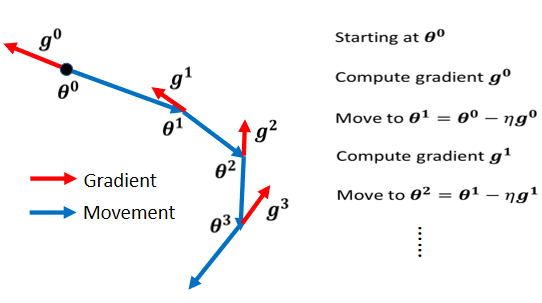
?一般的 Gradient Descent 是说,我们有一个初始的参数叫做,计算一下 Gradient,然后计算完这个 Gradient 以后呢,我们往 Gradient 的反方向去 Update 参数
?我们到了新的参数以后,再计算一次 Gradient,再往 Gradient 的反方向,再 Update 一次参数,到了新的位置以后再计算一次 Gradient,再往 Gradient 的反方向去 Update 参数,这个 Process 就一直这样子下去
(3)Gradient Descent + Momentum
加上 Momentum 以后,每一次我们在移动我们的参数的时候,我们不是只往 Gradient Descent,我们不是只往 Gradient 的反方向来移动参数,我们是?Gradient 的反方向,加上前一步移动的方向,两者加起来的结果,去调整去到我们的参数,
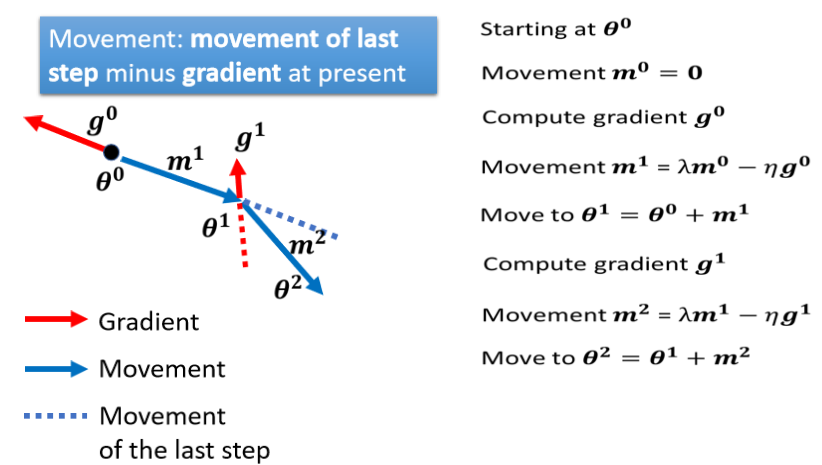
?
Critical Point(驻点)
1.训练失败的原因
- 做Optimization的时候,有时发现参数在updat时loss不再下降,
- 有时候你的model就train不起来,一开始你不管怎麼update你的参数,你的loss通通都掉不下去
saddle point(鞍点)
?gradient是零,但是不是local minima,也不是local maxima的地方,像在上边这个例子裡面 红色的这个点,它在左右这个方向是比较高的,前后这个方向是比较低的,它就像是一个马鞍的形状,所以叫做saddle point(鞍点)
为何区分local minima还是saddle point
因為如果是卡在local minima,那可能就没有路可以走了,因為四周都比较高,你现在所在的位置已经是最低的点,loss最低的点了,往四周走 loss都会比较高,你会不知道怎麼走到其他的地方去
但saddle point就比较没有这个问题,如果你今天是卡在saddle point的话,saddle point旁边还是有路可以走的,还是有路可以让你的loss更低的,你只要逃离saddle point,你就有可能让你的loss更低
?
数学推导
1.泰勒展开
如果给定某一组参数,比如说蓝色的这个 θ'?,在θ ′???附近的loss function,是有办法被写出来的,它写出来就像是这个
(1)第一项是?L(θ′),就告诉我们说,当θ跟θ ′?很近的时候,L(θ)应该跟L ( θ ′ ) 很靠近
(2)第二项是( θ ? θ ′ ) T g?
?g是一个向量,这个g就是我们的gradient
这个gradient会来弥补, θ'?跟θ之间的差距
?
(3)第三项跟Hessian有关,这边有一个H
?这个H叫做Hessian矩阵,H裡面放的是L的二次微分,它第i个row,第j个column的值,就是把θ的第i个component,对L作微分,再把θ的第j个component,对L作微分,再把θ的第i个component,对L作微分,做两次微分以后的结果?就是这个
?L(θ),这个式子跟两个东西有关係,跟gradient有关係,跟hessian有关係,gradient就是一次微分,hessian就是裡面有二次微分的项目
2.Hession矩阵
那如果我们今天走到了一个critical point,意味著gradient為零,也就是绿色的这一项完全都不见了
?g是一个zero vector,绿色的这一项完全都不见了,只剩下红色的这一项,所以当在critical point的时候,这个loss function,它可以被近似為L ( θ ′ ) 加上红色的这一项
?
θ′它是一个local minima,是一个local maxima,还是一个saddle point
?第三个可能是假设,v^T H v,有时候大於零 有时候小於零,代不同的v进去 代不同的θ进去,红色这个框框裡面有时候大於零,有时候小於零,意味著说在θ’附近,有时候L(θ)>L(θ’) 有时候L(θ)<L(θ’),在L(θ’)附近,有些地方高 有些地方低,这意味著这是一个saddle point
?
?vTHv都大于0,这种矩阵叫做正定矩阵,它所有的特征值都是正的
1.所有eigen value都是正的,那就代表说这个条件成立,代表说是一个local minima
2.若小于0,特征值就是负的,他是local maxima
3.那如果eigen value有正有负,那就代表是saddle point
saddle point(鞍点)
?H可以判断是否在saddle point,还能指出参数,update方向
?
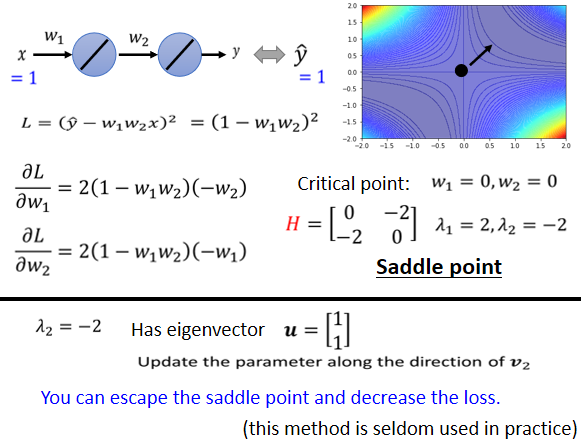
原点是一个critical point
这个Hessian有一个负的eigen value,这个eigen value等於-2,那它对应的eigen vector,它有很多个,其实是无穷多个对应的eigen vector
我们就取一个出来,我们取是它对应的一个eigen vector,那我们其实只要顺著这个u的方向,顺著
这个vector的方向,去更新我们的参数,就可以找到一个,比saddle point的loss还要更低的点
?以今天这个例子来看的话,你的saddle point在(0,0)这个地方,你在这个地方会没有gradient,Hessian的eigen vector告诉我们,只要往的方向更新,你就可以让loss变得更小,
然实际上,在实际的implementation裡面,你几乎不会真的把Hessian算出来,需要的运算量非常非常的大
训练中stuck ≠ 小梯度
1)People believe training stuck because the parameters are around a critical point
為什麼说这个critical point不
一定是我们训练过程中,最大的阻碍呢?
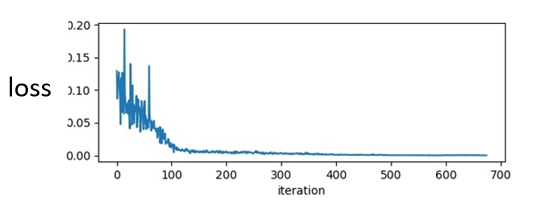
?在训练一个network的时候,你会把它的loss记录下来,所以你会看到,你的loss原来很大,随著你参数不断的update,横轴代表参数update的次数,随著你参数不断的update,这个loss会越来越小,最后就卡住了,你的loss不再下降
当我们说 走到critical point的时候,意味著gradient非常的小,但是你有确认过,当你的loss不再下降的时候,gradient真的很小吗?其实多数的同学可能,都没有确认过这件事,而事实上在这个例子裡面,在今天我show的这个例子裡面,当我们的loss不再下降的时候,gradient并没有真的变得很小
?
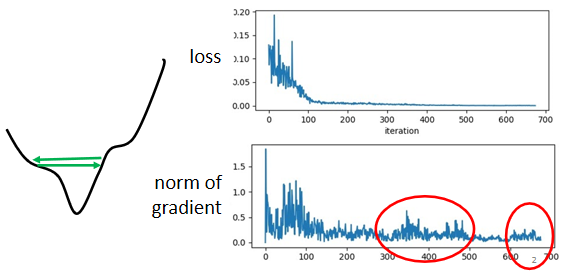
?
gradient是一个向量,下面是gradient的norm,即gradient这个向量的长度,随著参数更新的时候的变化,你会发现说虽然loss不再下降,但是这个gradient的norm,gradient的大小并没有真的变得很小
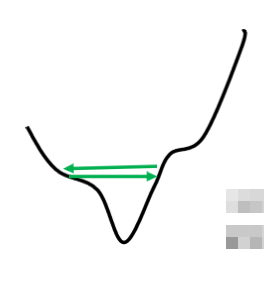
?这个是我们的error surface,然后你现在的gradient,在error surface山谷的两个谷壁间,不断的来回的震荡
它的gradient仍然很大,只是loss不见得再减小了
(2)Wait a minute
如果我们在训练的时候,其实很少卡到saddle point,或者是local minima,那这一个图是怎麼做出来的呢?
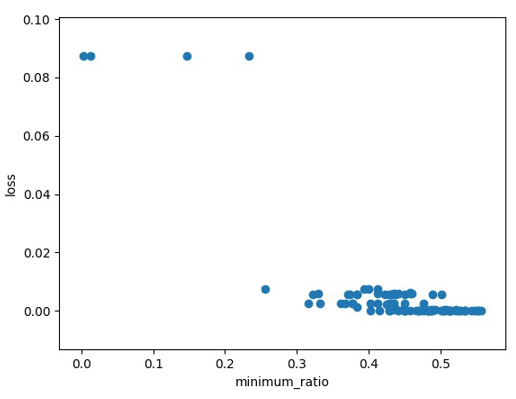
?我们现在训练一个Network,训练到现在参数在critical point附近,然后我们再来根据eigen value的正负号,来判断说这个critical point,比较像是saddle point,还是local minima
所以做完这个实验以后,我更感觉你要走到一个critical point,其实是困难的一件事,多数时候training,在还没有走到critical point的时候,就已经停止了,那这并不代表说,critical point不是一个问题,我只是想要告诉你说,我们真正目前,当你用gradient descend,来做optimization的时候,你真正应该要怪罪的对象,往往不是critical point,而是其他的原因,
?
(3)没有critical points时训练可能也困难
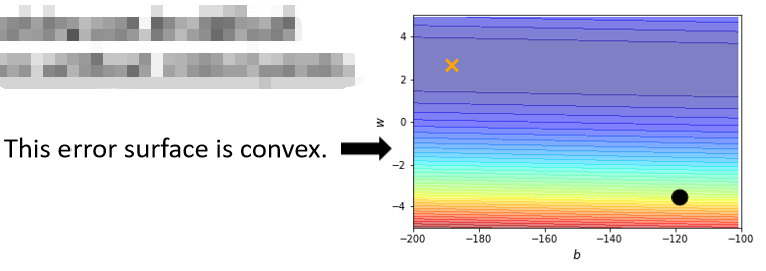
?我们只有两个参数,这两个参数值不一样的时候,Loss的值不一样,我们就画出了一个error surface,这个error surface的最低点在黄色X这个地方,事实上,这个error surface是convex的形状(可以理解为凸的或者凹的,convex optimization常翻译为“凸优化”)
?
那现在我们要从黑点这个地方,这个地方当作初始的点,然后来做gradient descend
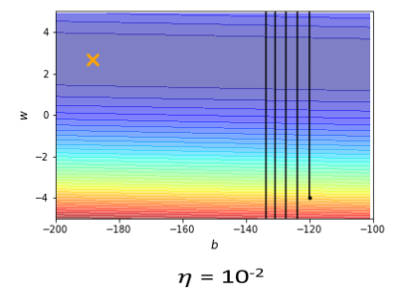
?learning rate设10?2的时候,我的这个参数在峡谷的两端,我的参数在山壁的两端不断的震盪,我的loss掉不下去,但是gradient其实仍然是很大的
那你可能说,就是因為你learning rate设太大了阿,learning rate决定了我们update参数的时候步 伐有多大,learning rate显然步伐太大,你没有办法慢慢地滑到山谷裡面只要把learning rate设小一点,不就可以解决这个问题了吗?
事实不然,因為我试著去,调整了这个learning rate,就会发现你光是要train这种convex的optimization的问题,你就觉得很痛苦,我就调这个learning rate,从10?2,一直调到10??,调到10??以后,终於不再震盪了
终於从这个地方滑滑滑,滑到山谷底终於左转,但是你发现说,这个训练永远走不到终点,因為我的learning rate已经太小了,竖直往上这一段这个很斜的地方,因為这个坡度很陡,gradient的值很大,所以还能够前进一点,左拐以后这个地方坡度已经非常的平滑了,这麼小的learning rate,根本没有办法再让我们的训练前进
?
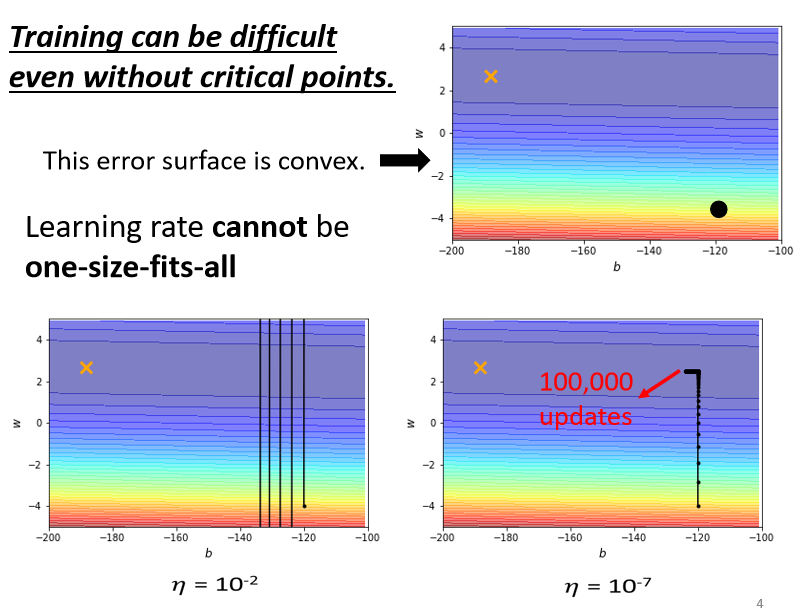
?显然就算是一个convex的error surface,你用gradient descend也很难train
4.梯度下降
(θ)
- L?:lossfunction(损失函数)
- θ?:parameters(参数)
我们要找一组参数?θ? ,让损失函数越小越好,这个问题可以用梯度下降法解决:
假设 θ 有里面有两个参数 θ 1 , θ 2
随机选取初始值
?
?η?叫做Learning rates(学习速率)
5. 调整学习速率
上图左边黑色为损失函数的曲线
假设从左边最高点开始,如果学习率调整的刚刚好,比如红色的线,就能顺利找到最低点。
如果学习率调整的太小,比如蓝色的线,就会走的太慢,虽然这种情况给足够多的时间也可以找到最低点,实际情况可能会等不及出结果。
如果 学习率调整的有点大,比如绿色的线,就会在上面震荡,走不下去,永远无法到达最低点。
还有可能非常大,比如黄色的线,直接就飞出去了,更新参数的时候只会发现损失函数越更新越大。
解决方法就是上图右边的方案,将参数改变对损失函数的影响进行可视化。比如学习率太小(蓝色的线),损失函数下降的非常慢;学习率太大(绿色的线),损失函数下降很快,但马上就卡住不下降了;学习率特别大(黄色的线),损失函数就飞出去了;红色的就是差不多刚好,可以得到一个好的结果。
自动调整学习率η?
学习率不能是一个值通用所有特征,不同的参数需要不同的学习率
(1)均方根Root mean square
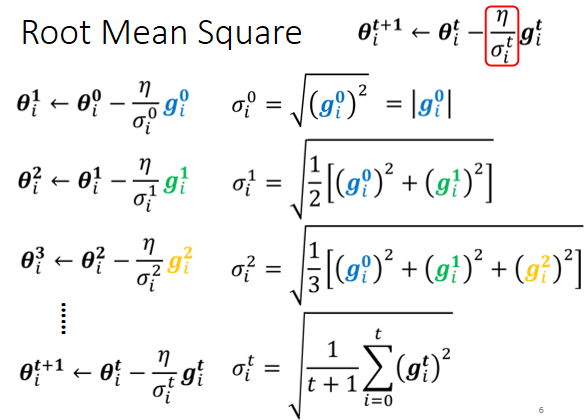
?
?
Adagrad 算法
每个参数的学习率都把它除上之前微分的均方根
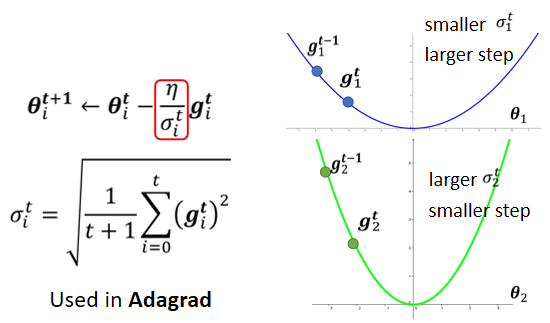
(3)RMSProp
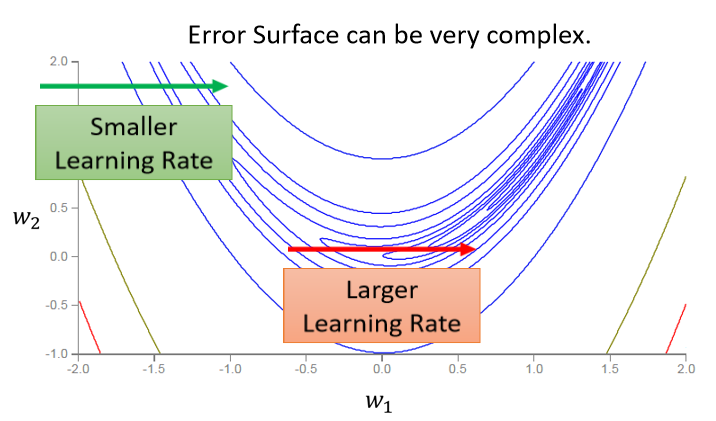
走到了中间这一段,到了红色箭头的时候呢,坡度又变得平滑了起来,平滑了起来就需要比较大的learning rate,所以就算是同一个参数同一个方向,我们也期待说,learning rate是可以动态的调整的,于是就有了一个新的招数,这个招数叫做RMS Prop
?
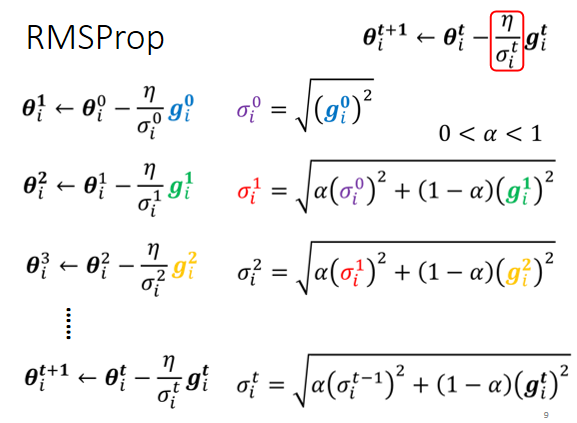
?Optimization总结

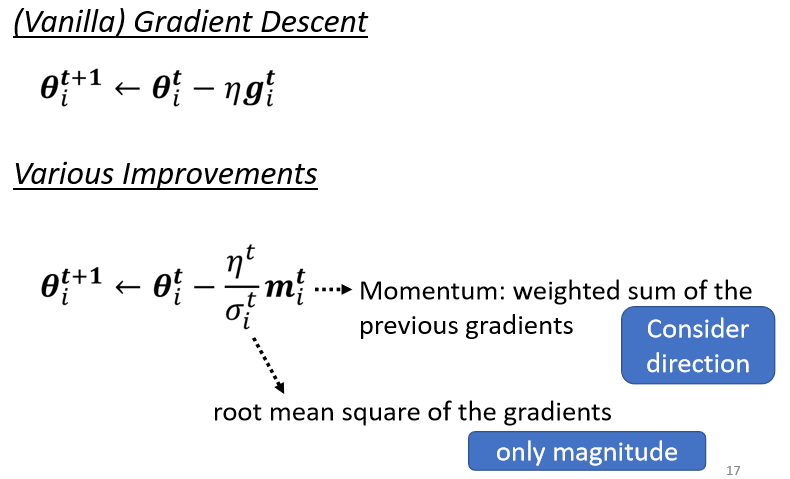
我们有Momentum,也就是说我们现在,不是完全顺著gradient的方向,现在不是完全顺著这一个时间点,算出来的gradient的方向,来update参数,而是把过去,所有算出来gradient的方向,做一个加总当作update的方向,这个是momentum
接下来应该要update多大的步伐呢,我们要除掉,gradient的Root Mean Square
?
?
,这一个momentum是考虑,过去所有的gradient,这个σ也是考虑过去所有的gradient,一个放在分子一个放在分母,都考虑过去所有的gradient,不就是正好抵销了吗,
但是其实这个Momentum跟这个σ,它们在使用过去所有gradient的方式是不一样的,Momentum是直接把所有的gradient通通都加起来,所以它有考虑方向,它有考虑gradient的正负号,它有考虑gradient是往左走还是往右走
但是这个Root Mean Square,它就不考虑gradient的方向了,它只考虑gradient的大小,记不记得我们在算σ的时候,我们都要取平方项,我们都要把gradient取一个平方项,我们是把平方的结果加起来,所以我们只考虑gradient的大小,不考虑它的方向,所以Momentum跟这个σ,算出来的结果并不会互相抵销掉
?
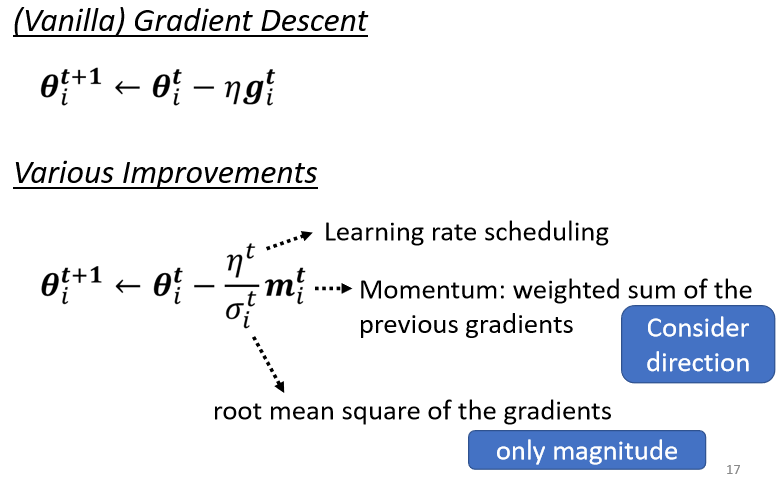
那最后我们还会加上,一个learning rate的scheduling,
?
?
改变Landscape的必要性
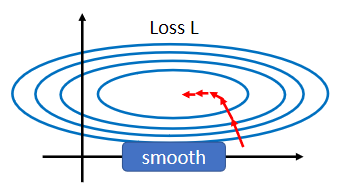
假设你的两个参数啊,它们对 Loss 的斜率差别非常大,在 w 1??这个方向上面,你的斜率变化很小,在 w 2?这个方向上面斜率变化很大
如果是固定的 learning rate,你可能很难得到好的结果,所以我们才说你需要adaptive 的 learning rate、 Adam 等等比较进阶的 optimization 的方法,才能够得到好的结果
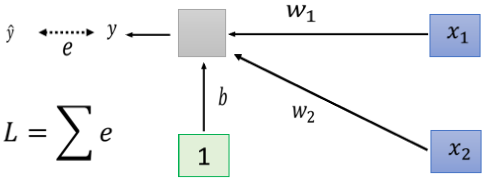
?
所有 training data e 加起来就是你的 Loss,然后去 minimize 你的 Loss
(1)啥时候会出现比较不好 train 的 error surface 呢?

?

?

?(2)Feature Normalization

?

?

?(1)那怎麼对 z 做 Feature Normalization 呢

?
?
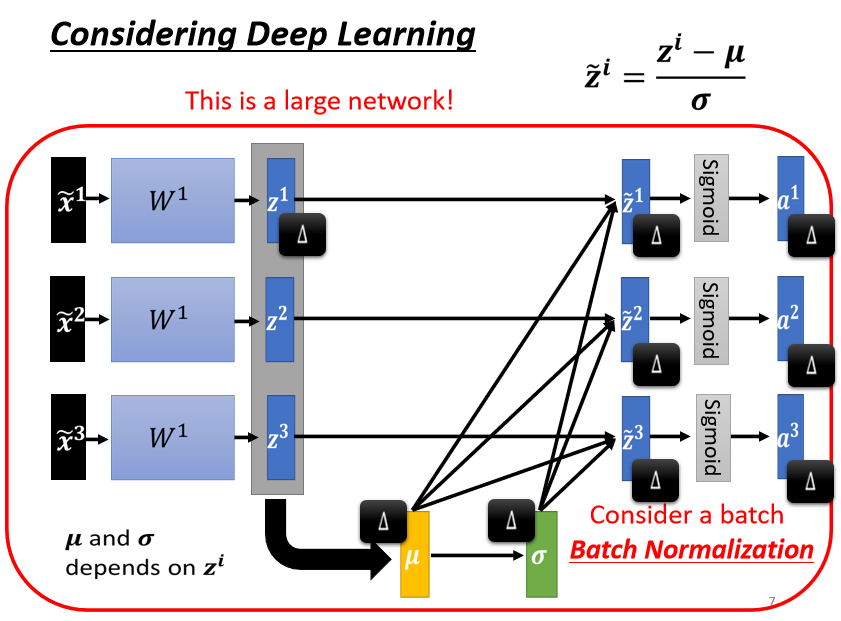
?
也就是说,你现在有一个比较大的 network
你之前的 network,都只吃一个 input,得到一个 output
现在你有一个比较大的 network,这个大的 network,它是吃一堆 input,用这堆 input 在这个 network 裡面,要算出 μ 跟 σ 然后接下来產生一堆 output
?
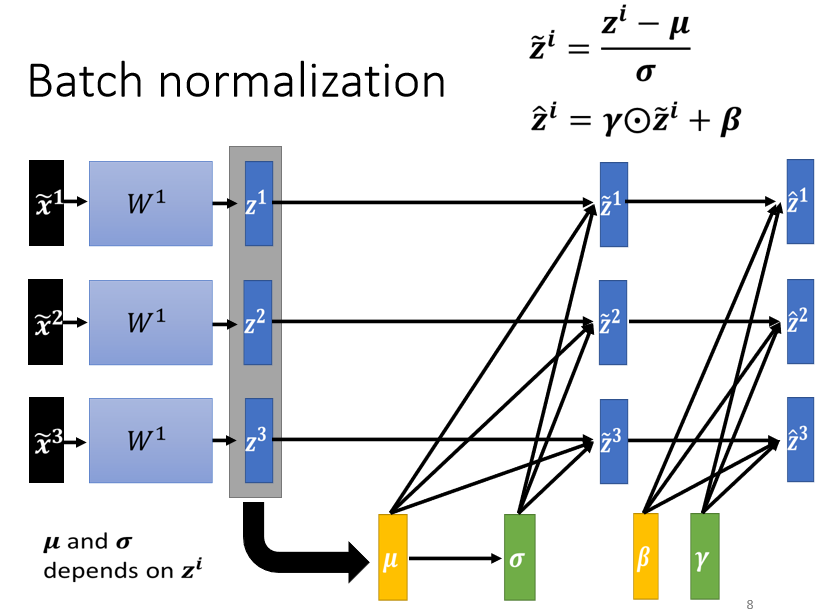
?
3.Testing
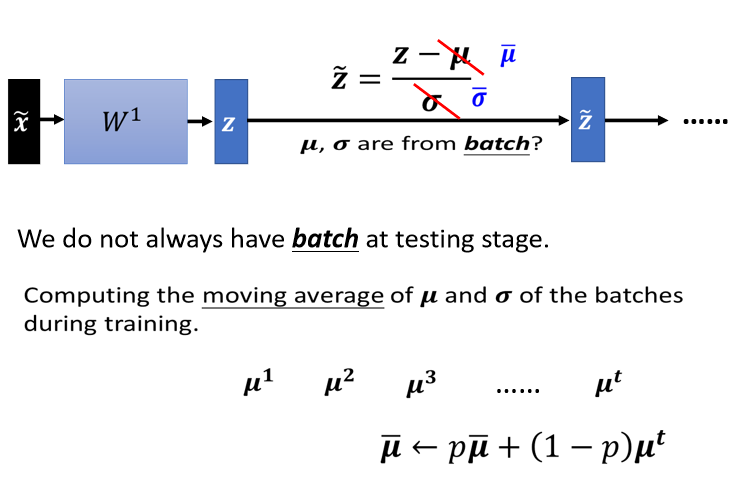
?






















