一、前言
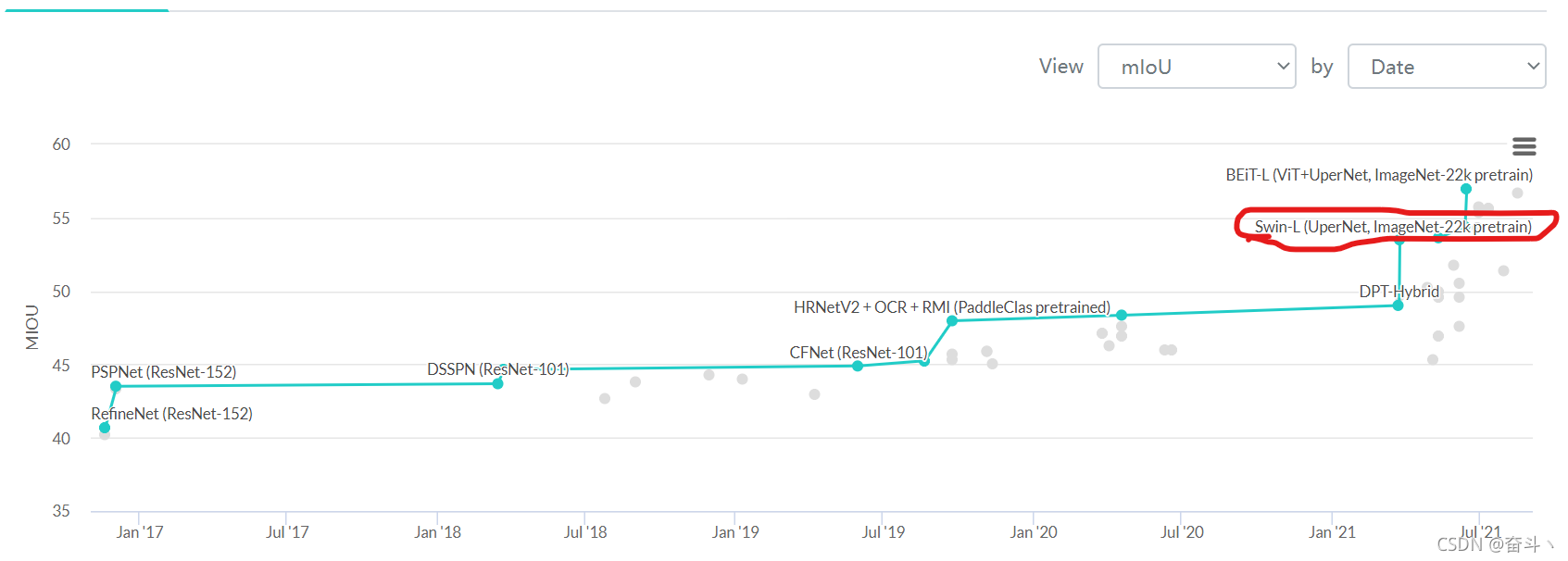
一张图告诉你Transformer现在是多么的强!几乎包揽了ADE20K语义分割的前几名!
该文章详细解读Swin-transformer的相关内容以及高明之处。看完学不会,你在评论区打我!CNN已然在计算机视觉领域取得了革命性的成果,拥有着不可撼动的地位。Transformer最初用于NLP领域,但Transformer凭借其强大的特征表征能力,已经在cv领域杀出了一条血路。
paper链接:https://arxiv.org/pdf/2103.14030.pdf
代码链接:https://github.com/microsoft/Swin-Transformer
二、Swin Transformer
2.1 背景
Transformer最开始用于NLP领域,但其强大的表征能力让cv领域的研究人员垂涎欲滴。然而从NLP转为cv领域,存在两个天然的问题。
- 1.相较于文本,图像中像素的分辨率更高
- 2.图像的视觉实体尺寸之间差异很大
传统Transformer(例如transformer、ViT等)尽管有强大的特征表达能力,但其巨大计算量的问题让人望而却步。与传统Transformer不同的是,Swin-Transformer解决了Transformer一直饱受诟病的计算量问题。那么,Swin-Transformer是如何解决的计算量问题呢?让我们继续往下看吧。
2.2 Architecture概况
学习swin transformer之前,我们首先需要熟知以下几个概念:
- Resolution:假设一张图像的分辨率为224x224,这里所说的224就是像素。
- Patch:所谓的Patch就是由多少个像素点构成的,假设一个patch的size为4x4,则这个patch包含16个像素点。
- Window:window的size是由patch决定的,而不是由像素点,假设window的size为7x7,则该window包含49个patch,而不是49个像素点。
在对swin-transformer网络进行讲解之前,我们首先需要明确一点:无论是transformer还是swin-transformer结构,都不会改变输入的形状,换句话说,输入是什么样,经过transformer或swin-transformer后,输出跟输入的形状是相同的。
一般而言,我拿到一篇论文之后,会首先分析每个块的输入输出是怎样的,先从整体上对网络结构把握,然后在慢慢的细化。我们首先来梳理一下swin-transformer每个块的输入输出。

| stage | Layer | size |
|---|---|---|
| input image | 224x224x3 | |
| patch partition | 224/4 x 224/4 x 4x4x3 | |
| 1 | linear embedding | 224/4 x 224/4 x 96 |
| 1 | swin transformer | 224/4 x 224/4 x 96 |
| 2 | patch merging | 224/8 x 224/8 x 192 |
| 2 | swin transformer | 224/8 x 224/8 x 192 |
| 3 | patch merging | 224/16 x 224/16 x 192 |
| 3 | swin transformer | 224/16 x 224/16 x 192 |
| 4 | patch merging | 224/32 x 224/32 x 384 |
| 4 | swin transformer | 224/32 x 224/32 x 384 |
从结构图中可以看到,swin-transformer网络结构主要包括以下层:
- 1.Patch Partition:将输入图像划分为若干个patch
- 2.Linear Embedding:将输入图像映射要任意维度(论文中记为C,即C=96)
- 3.Patch Merging:降低分辨率,扩大感受野,获得多层次的特征信息,类似于CNN中的pool层
- 4.swin transformer:特征提取及特征表征
2.3 swin-transformer结构解析
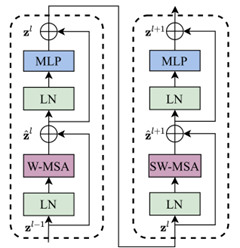
到这里我们已经大致了解swin-transformer网络的基本结构,接下来,跟着我一块揭开Swin-transformer的真面目吧。一个swin-transformer block由两个连续的swin-transformer结构组成,两个结构不同之处在于:第一个结构中使用的是在一个window中计算self-attention,记为W-MSA;第二个结构中使用的是shifted window技术,记为SW-MSA。 在这一章节中,我们重点介绍swin-transformer是如何在一个window中进行self-attention计算的。
假设我们将window size设置为4,则一个window中包含4x4个Patch,如下图中的Layer l的不重叠窗口划分结果。但只在window中进行self-attention计算,使得各个windows之间缺乏信息的交互,这限制了swin-transformer的特征表达能力。
为此,swin-transformer的作者提出了top-left的窗口移位方式,如下图中Layer l+1所示。但这样的window移位方式增加了window的数量(从2x2->3x3),增加了2.25倍,且window之间的size也不尽相同,这导致无法进行并行计算。
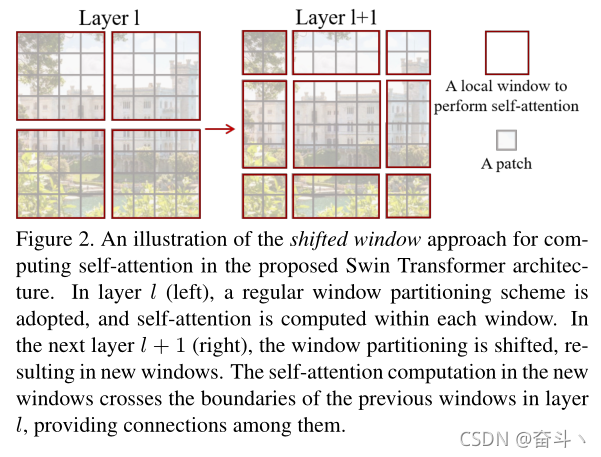
基于上述两个原因,作者提出了shifted window技术,这也是整篇文章的核心所在。那么shifted window的过程是怎样的呢?
2.4 shifted window
假设input image的size为224x224,window的size为7x7,patch size为4X4,那么input image包含224/4 x 224/4个patch(56x56),如下图中的第一张图。我们将其划分为不重叠的window,每个window包含7x7个patch,如下图中的第2张图。接下来,我们将整张图像沿主对角线方向移位(floor(M/2),floor(M/2))个patch,这里的M代表window的size,则本例中移位(3,3)个patch,如第3张图所示。移位后,可以看到,一个window包含4个不同window的部分,如第4张图所示(蓝色网格线)。
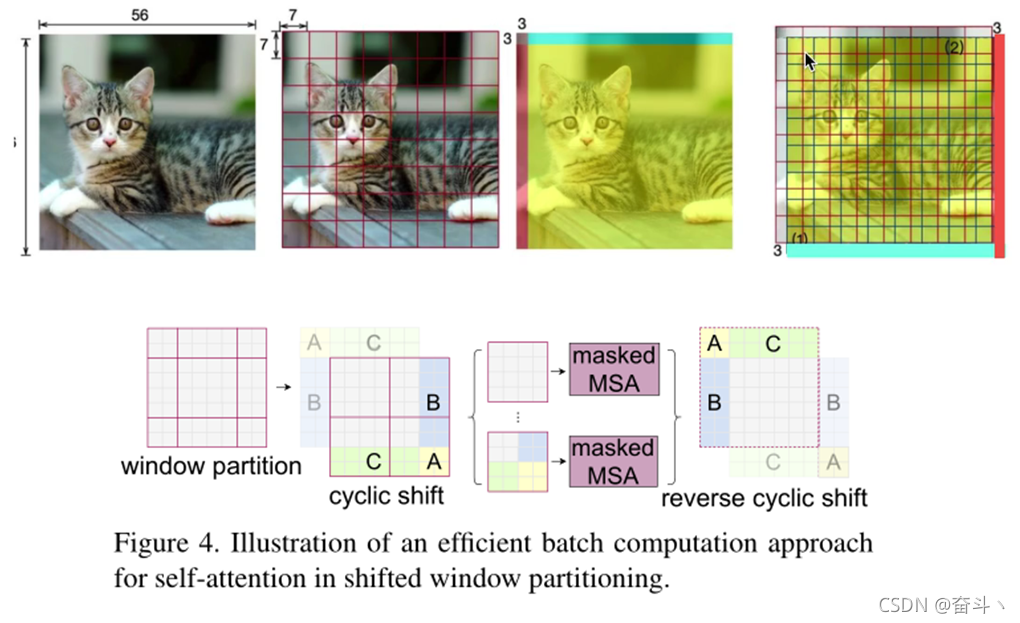
我们假设移位后的图像是如下图所示的。我们分别对不同的区域进行编码,为什么要进行编码呢?这是因为我们对一个window中不同区域Patch进行self-attention计算没有任何意义。例如,区域3和区域4在原图中就是两个不相邻的区域,本身之间没有任何的联系。那么,swin-transformer是如何实现一个window中只有相同区域才进行self-attention计算的呢?

我们以右下角4个均不同的区域为案例进行演示。为简洁,我们将右下角的一个window进行简化,由原来的49个patch简化为4个patch,但过程是相同的。
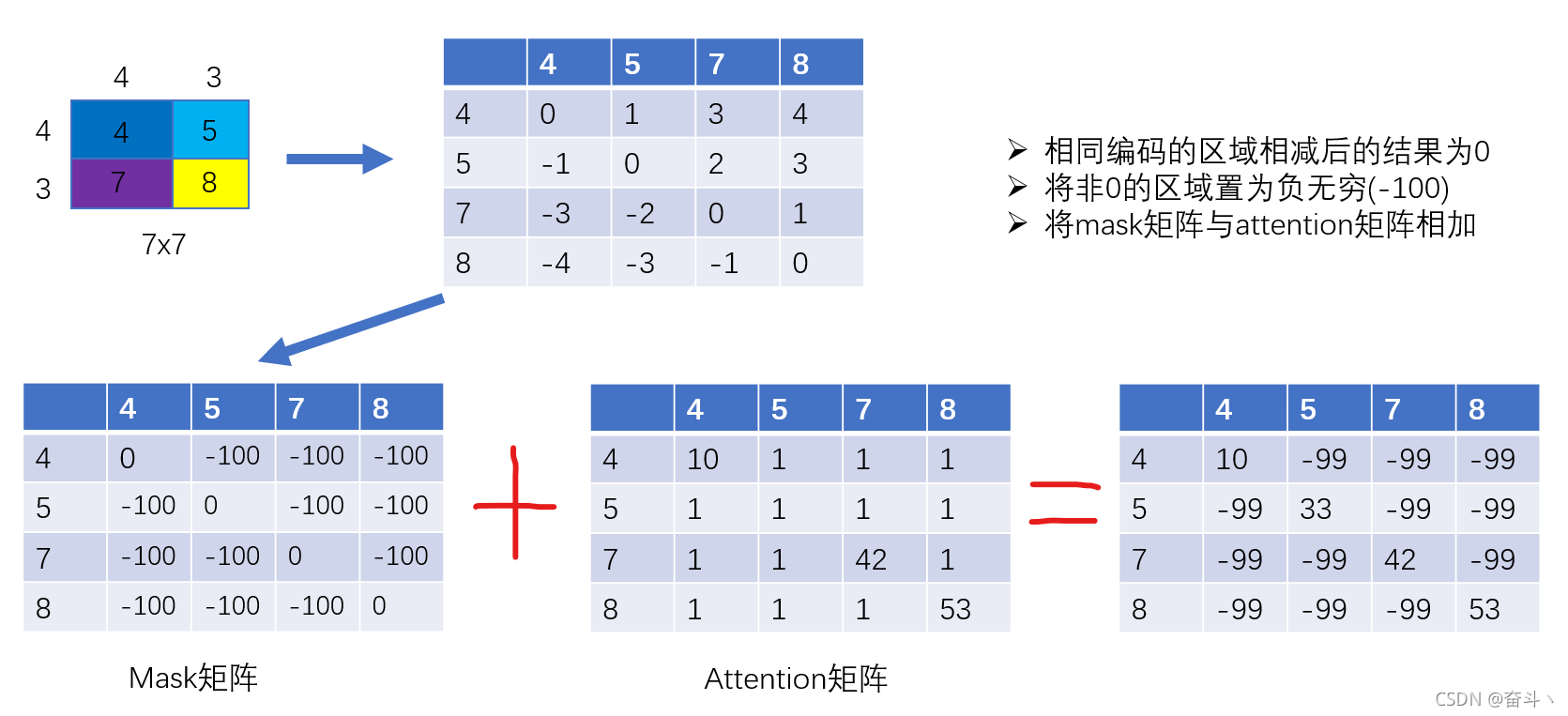
首先我们根据patch的数量建立一个相关矩阵,本例中patch的数量为4,则建立一个4x4的矩阵,然后将x和y进行相减,相减后,相同区域的结果为0,不同区域的结果我们将其置为负无穷,得到一个mask矩阵,然后与计算得到的attention矩阵进行相加,这样便实现了相同区域进行self-attention计算。
2.5 Relative position bias

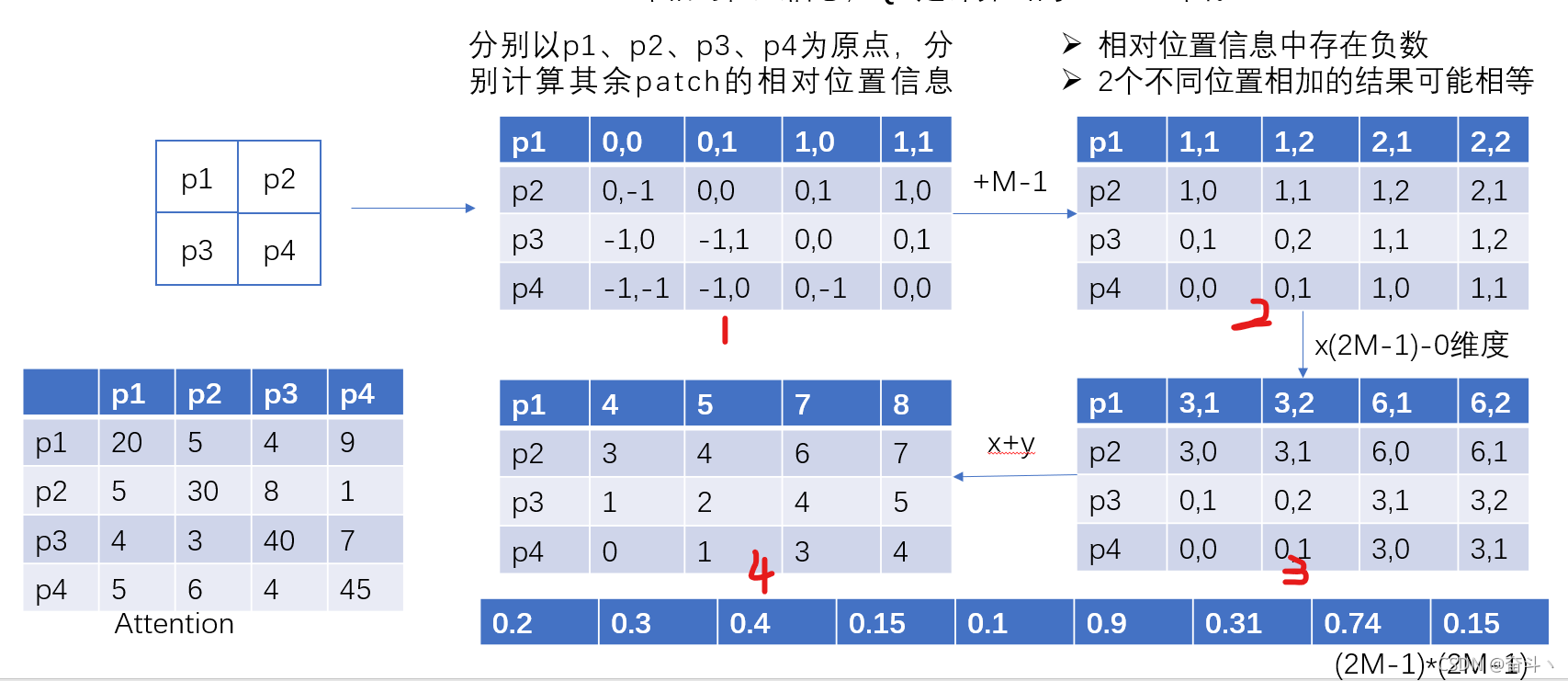
公式中的B即为相对位置信息。那么相对位置信息是如何计算的呢?我们假设有p1、p2、p3、p4四个patch,分别以p1、p2、p3、p4为原点,计算其余patch相对于原点的偏移量,如表1所示。计算完毕后,我们会发现有以下2个问题:
- 1.相对位置信息中出现负数
- 2.(0,1)和(1,0)虽然是2个不同的相对位置信息,但是它们相加的总偏移量相等。
为了解决以上2个问题,论文作者做了如下操作: - 1.为了方便后续计算,每个坐标的位置都加上偏移量,使其从0开始,避免负数的出现。
- 2.对0维度进行乘法变换,论文中是对0维度的数值乘以(2M-1)。
- 3.将0维度和1维度的数值进行相加,得到一个index值。
- 4.根据index的值,映射到权重矩阵中得到相应的权重值。
- 5.将attention矩阵与权重矩阵进行相加。
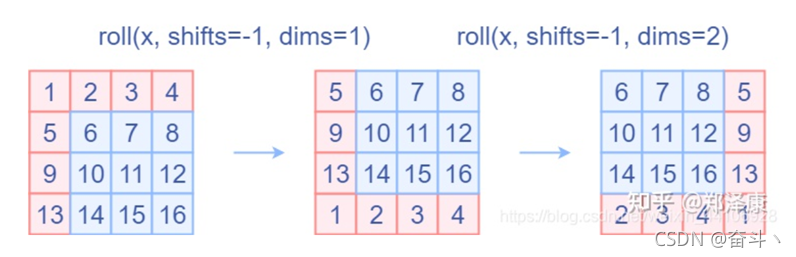
2.6 循环窗口移动技术是如何实现的
其实原理很简单,就是使用了torch.roll()这个方法,关于方法的解释及代码如下,大家可以了解一下。