[人工智能]图解反向传播算法

图解反向传播算法

在训练神经网络时，前向传播是网络从接收输入 $x$ 直到它产生一个标量代价函数 $J(\theta )$ ，反向传播（BP）则是代价函数的信息通过网络向后流动并计算梯度。计算图可以准确地描述网络的前向和后向过程，而且代码实现图这种数据结构后，可以利用到图的遍历、拓扑排序等经典算法来实现通用的BP算法。

参考资料：
花书《深度学习》第六章
自动微分开源项目：https://gitee.com/Carl-Xie/AutodiffEngine

问题引入

训练神经网络时，需要计算参数的梯度。而神经网络本质上是一个复合函数，对于复合函数的求梯度可以使用链式法则，但直接使用链式法则会有重复计算梯度的问题。BP算法就是用于求复合函数导数的一种算法，并且它运用了动态规划的思想从而避免了直接使用链式时的重复计算梯度的问题。下面先简单地介绍一下计算图和链式法则的相关概念，然后利用计算图来说明BP算法是如何避免重复计算梯度的，最后用python代码实现计算图和BP算法。

计算图

计算图是一个有向无环图，图中的每个结点表示一个变量，变量可以是一个标量、向量、矩阵、张量。图中的任何一个结点都会关联一个产生它的操作，即一切结点都是由操作产生的。操作是指一个或多个变量的简单函数。我们可以通过将多个操作复合在一起来描述更为复杂的函数，在图中的表现就是将多个结点用有向边连接起来构成复合函数。下面是一些计算图的示例。

(a) 使用$\times$操作计算 $z=xy$ 的图。(b) 令 $w\in \mathbb{R}$ 为图的输入，用操作函数 $f:\mathbb{R}\to \mathbb{R}$ ，构造的一个复合函数 $z=f(f(f(w)))$ 。(c ) 逻辑回归的预测结果 $\hat{Y}=\sigma (XW+b)$ 以及交叉熵损失函数 $CE$ 。

计算图是一个有向无环图，一个含有 $n$ 个结点的计算图最多有 $n(n?1)/2$ 条边。如果两个结点之间有一条边相连，我们把箭尾侧的结点称为父结点，箭头侧的结点称为子结点。举个例子 $x\to y$ ，其中 $x$ 是父结点，$y$ 是子结点。

链式法则

微分中的链式法则是用来计算复合函数导数的。设 $x$ 是实数，$f$ 和 $g$ 是从实数映射到实数的函数。假设 $y=g(x)$ 并且 $z=f(g(x))=f(y)$ ，那么链式法则就是
$$\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$$将 $z$ 保持为标量，而把标量 $x$ 和 $y$ 扩展到张量 $X$ 和 $Y$ 的情况，使用链式法则求偏导数 $\frac{?z}{?X}$：
(1).首先把张量 $Y$ 和张量 $X$ 展平后得到向量 $y$ 和 向量 $x$ ，然后向量 $y$ 对向量 $x$ 求偏导数得到矩阵 $\frac{?y}{?x}$ ，这个矩阵就是Jacobian矩阵
(2).那么 $z$ 对展平后的 $X$ ,即 $x$ 的偏导数可以写成如下形式：
$$\frac{?z}{?x}=\frac{?z}{?y}\frac{?y}{?x}=\sum _j\frac{?z}{?y_j}\frac{?y_j}{?x}$$其中 $y_j$ 是向量 $y$ 的分量。这个 $\frac{?z}{?y}\frac{?y}{?x}$ 表示的就是一个向量乘以Jacobian矩阵，将这个乘积称为Jacobian向量积。如果把 $x$ 想象成一个标量，那么 $\frac{?z}{?y}\frac{?y}{?x}$ 表示的就是两个向量的内积，基于此所以叫做Jacobian向量积。现在我们仅看上式中的最左边和最右边两项，并把 $x$ 重新排列回去称为张量 $X$ ，则Jacobian向量积的结果变为张量的形式：
$$\frac{?z}{?X}=\sum _j\frac{?z}{?y_j}\frac{?y_j}{?X}$$并且注意到 $\frac{?z}{?X}$ 与 $X$ 是同维的张量，这对编程实现BP算法是有利的。我们把这个求和式也叫做Jacbian向量积。最终，计算图中所有变量的梯度都能用一个Jacobian向量积来表示。

BP算法的计算图

原始的计算图中，每个结点的梯度都能用Jacobian向量积表示，我们可以在原始的计算图中添加一些额外的结点，这些额外的结点提供了我们所需梯度的计算过程。这样一来，计算梯度的过程只是在跑另一张计算图而已。下图是一个在原始图中添加额外结点计算梯度的示例。

我们假设计算图中的每个结点都关联着一个操作，这个操作表示了该结点是如何产生的，操作就是一个函数，它把输入结点映射到该结点。结点的定义如下：

class Node(object):
    # 构造器，主程序不使用这个构造器
    def __init__(self):
        self.input_nodes: List[Node] = []  # 输入结点列表
        self.op: Operation = None          # Operation类对象
        self.name: str = ""                # 结点名称

    # 构造器，主程序只使用这个带参构造器
    @classmethod
    def instance(cls, input_nodes: List, op: Operation, name: str):
        node = cls()
        node.input_nodes = input_nodes
        node.op = op
        node.name = name
        return node

我们规定一切结点都是由操作产生的，包括自变量结点、常量结点这种仿佛“不需要输入结点”的结点也可以看作是由操作产生的，例如可以定义占位符操作来产生自变量结点、定义常量操作来产生常量结点。操作的本质就是一个函数，通过这个函数可以产生操作结果的结点，也可以得到操作结果的具体数值。每个操作也与gradient操作相关联，该gradient操作就是用来计算Jacobian向量积。操作的定义如下，Operation 类是一个接口，三个方法：

1. __call__() 产生操作结果结点
2. compute() 方法计算操作结果的具体数值
3. gradient(output_grad: Node, node: Node) -> List[Node] ，其中 output_grad 该结点的梯度，对应Jacobian向量积中的 $\frac{?z}{?y}$ ，node 是操作的结果结点。最终返回的是一个List[Node]对象，列表中各个值对应着每个输入结点的梯度。

class Operation():
    def __call__(self, input_nodes: List[Node], name: str) -> Node:
        pass

    # input_vals与调用call方法时的input_nodes参数是一一对应的关系
    def compute(self, node: Node, input_vals: List[]) -> np.ndarray:
        pass
    
    # input_nodes与调用call方法时的input_nodes是相同的
    def gradient(self, output_grad: Node, node: Node)-> List[Node]:
        pass

这里展示 Operation 类的一个具体实现，矩阵相乘操作 MatMulOp

class MatMulOp(Operation):
    def __call__(self, input_nodes: List[Node], name=""):
        new_node = Node.instance(input_nodes, self, name)
        return new_node
    
    def compute(self, node, input_vals):
        mat_A = input_vals[0]
        mat_B = input_vals[1]
        return np.matmul(mat_A, mat_B)

    # 其中，transOp是转置操作，其详细代码在附录部分
    def gradient(output_grad, node):
        A = node.input_nodes[0]
        B = node.input_nodes[1]
        G = output_grad
        # 返回矩阵A和B的梯度，分别是G·B^T和A^T·G
        return [matmul_op(G, trans_op(B)), matmul_op(trans_op(A), G)]

matmul_op = MatMulOp()
trans_op = TransOp()

至此，计算图的部分已经准备完成。下面开始说明BP算法的本质思想–表填充策略，假设结点 $X$ 的子结点集合为 $Pa(X)$ ，那么梯度 $\frac{?z}{?X}$ 就是各个子结点的Jacobian向量积之和：
$$\frac{?z}{?X}=\sum _{Y\in Pa(X)}\frac{?z}{?Y}\frac{?Y}{?X}$$仔细观察上式，若将 $\frac{?z}{??}$ 看作 $dp[?]$ ，那么公式变为动态规划的状态转移方程
$$dp[X]=\sum _{Y\in Pa(X)}dp[Y]\frac{?Y}{?X}$$而初始条件是 $dp[z]=1$ ，即 $\frac{?z}{?z}=1$ 。动态规划的思想启示我们，采用表填充策略以空间换时间，首次遇到 $dp[X]$ 时才计算，计算完毕后保存起来，下次需要用到时就直接从存储中获取。具体的算法的python伪代码，如下。

# 主程序，z：输出结点，node_list：要求梯度的结点集合
def bp_diff(z: Node, node_list: List[Node]) -> List[Node]:
    dp = {} # 记录表
    dp[z] = constOp(1) # 常量操作产生常量1结点
    grad_node_list = []
    # 由于结点的属性记录了父结点input_nodes，没有记录它的子节点
    # 所以要先遍历图，把所有结点的子节点都找出来，并存储到map中
    node_to_son_map = find_son(z)
    for x in node_list:
        grad_x = build_grad(dp, node_to_son_map, x)
        grad_node_list.append(grad_x)
    return grad_node_list

def build_grad(dp: dict, node_to_son_map: dict, x: Node):
    if dp[x] is not None:
        return dp[x]
    sons = node_to_son_map[x]
    if sons is None:
        # 与z结点无关的结点才会走入这个分支
        dp[x] = zero_like_op([x], "")
        return dp[x]
    
    jacobian_list = []
    for y in sons:
        # 计算每个子节点的jacobian向量积
        y_grad = build_grad(dp, node_to_son_map, y)
        # 以下两行可以优化为用map来存储jacobian_of_input，避免多次计算
        jacobian_of_inputs = y.op.gradient(y_grad, y)
        x_idx = y.inputs.index(x)
        
        jacobian = jacobian_of_inputs[x_idx]
        jacobian_list.append(jacobian)
    # 将所有子结点的jacobian向量积加起来就是x结点的梯度
    dp[x] = sum_jacobian(jacobian_list)
    return dp[x]

def find_son(root: Node) -> dict[Node : List[Node]]:
    # 具体放在附录部分
    pass
def sum_jacobian(node_list: List[Node]):
    pass

BP算法在原始图中的每条边添加了 $o(1)$ 个Jacobian向量积的结点。因为就是拿图是有向无环图，它至多有 $o(n^2)$ 条边。对于实践中常用的神经网络的代价函数大致是链式结构的，使得方向传播只有 $o(n)$ 的成本。下图对比了BP算法和简单的链式法则在原始图中添加的Jacobian结点数目，可以看到简单的链式法则计算结点的梯度时会“重新计算一遍”一起计算过的梯度，这使得计算图变得庞大而冗余。

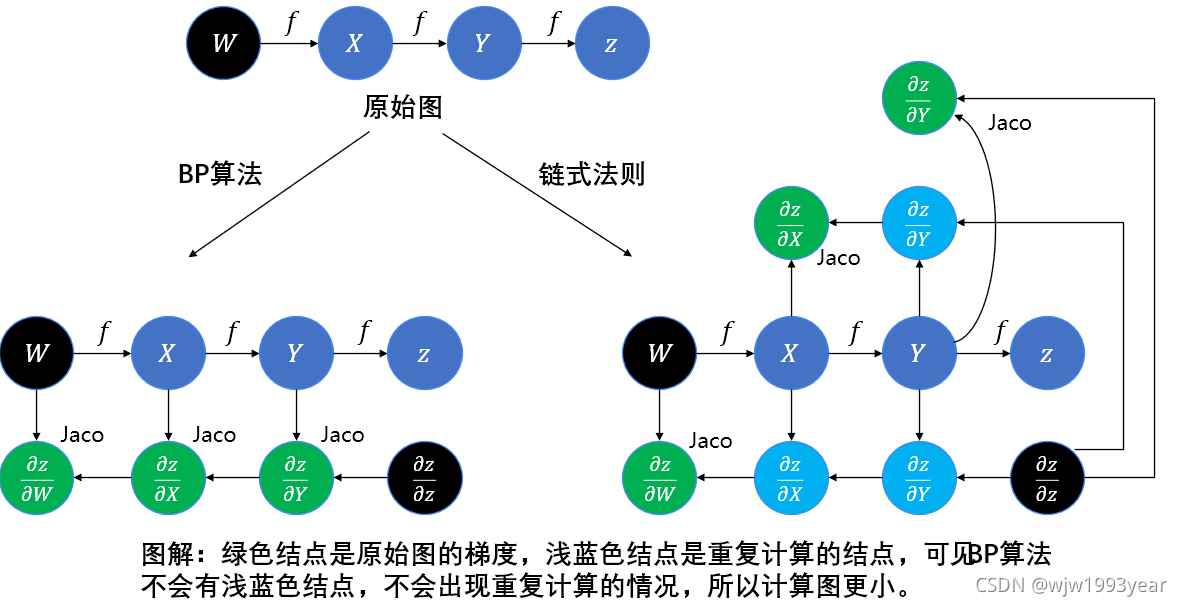
自底向上的BP

上述python伪代码实现的BP算法采用了递归的编程结构，这是一种自顶向下的算法，与之相对的，我们也可以采用自底向上的算法来实现，把递归的结构变为了循环迭代的结构。具体地，先对原始计算图的结点，按照输出结点靠前而输入结点靠后的原则进行拓扑排序，然后按照拓扑排序的顺序求：①每个结点的jacobian向量积以及②对其input_nodes的jacobian向量积。

def bp_diff_iter(z: Node, node_list: List[Node]) -> List[Node]:
    topo_order = reversed(find_topo_sort(z))
    grad_table = {}  # 梯度表
    node_to_jacobians = {z: [Constant(1)]}  # 雅可比向量积
    for y in topo_order:
        grad_y = sum_jacobian(node_to_jacobians[y])
        grad_table[y] = grad_y
        # y的各个输入结点的jacobian向量积，与y。input_nodes是一一对应的
        jacobian_of_inputs = y.op.gradient(grad_y, y)
        for i in range(len(y.input_nodes)):
            x = y.input_nodes[i]
            grad_x = jacobian_of_inputs[i]
            if x not in node_to_jacobians:
                node_to_jacobians[x] = [grad_x]
            else:
                node_to_jacobians[x].append(grad_x)

    grad_node_list = [grad_table[node] for node in node_list]
    return grad_node_list
                
# 拓扑排序
def find_topo_sort(z: Node) -> List[Node]:
    pass
def sum_jacobian(node_list: List[Node]):
    pass

上面的算法有个缺点，外循环是 for y in topo_order ，也就是它会求出所有结点的梯度，而不是只去求我们需要的 node_list 中的梯度。如要改善算法，可以在外循环里边加个判断，当 node_list 中的结点梯度都被求出来后，就停止。

自问自答

为什么叫做反向传播算法，“反向”的思想体现在哪？
用计算图去理解，对于一个计算图（模型/神经网络），把从输入结点到输出点的方向称为“前向”。在训练模型时，要求输出结点对图中每个结点的梯度值，而在求某个结点的梯度值时，总是要先求该结点的祖先结点的梯度值，在求完所有祖先结点的梯度值后，才能求该结点的梯度值，也就是说，整个梯度求解过程的方向是先求输出结点的梯度，再求父结点的梯度，依次下去。梯度求解的方向是从输出结点到输入结点，与“前向”过程的方向刚好相反，因此称为反向传播算法。

为什么BP算法可以减少重复计算？
因为Jacobian向量积可以写成动态规划的状态转移方程。将 $\frac{?z}{??}$ 看作 $dp[?]$ ，那么状态转移方程为：
$$dp[X]=\sum _{Y\in X.children}dp[Y]\frac{?Y}{?X}$$初始条件是 $dp[z]=1$ 。动态规划的本质就是记忆化递归，计算完某个结点的梯度后，会将其存储到map中，下次要使用的时候，就不必重新计算，而是从map中直接获取。在计算图中各个结点的梯度时，越靠近输出侧的结点的梯度会被越多次地重复使用，如果每次需要用到某个结点的梯度时都计算一次，那计算量是指数级别的，所以BP算法把这些结点的梯度值存储起来可以减少计算量，具体计算的复杂度是 $o(n)$ ，其中 $n$ 是计算图中的边数。

附录：计算图和BP的代码实现

设计思路：由操作决定结点的类型，一切结点都由且只能由操作产生，例如，常数结点由常数操作产生，自变量结点由占位符操作产生，需要什么样的结点，就要先定义什么样的操作，“操作是灵魂，结点是身体”。程序结构如下图。

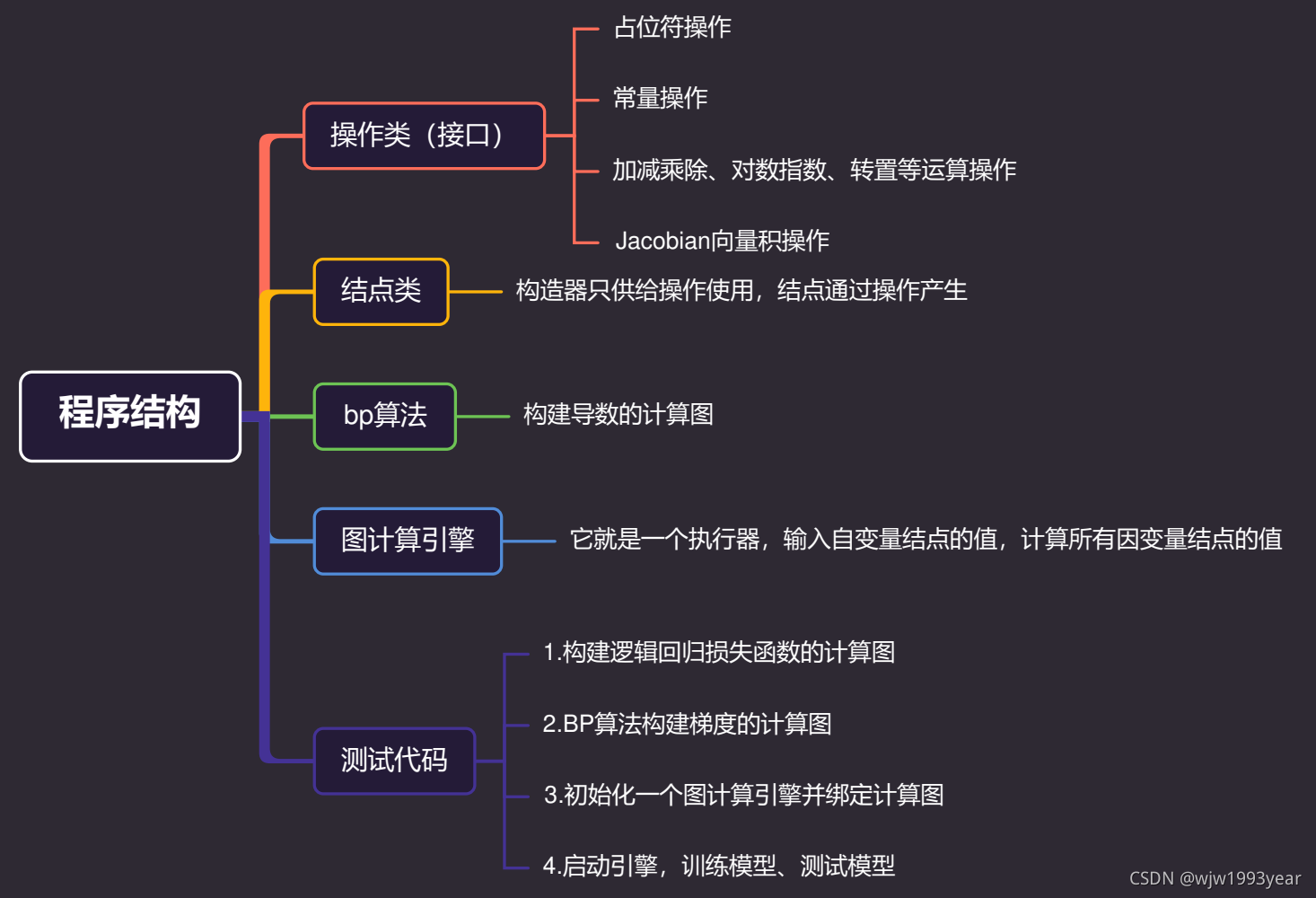
具体代码参考gitee地址：https://gitee.com/wjw1993year/learn-python.git，这里展示的是 autodiff.py 文件

from typing import List
import numpy as np


# 操作类接口
class Operation(object):
    """
    操作：返回操作结果结点
    input_nodes: 输入结点列表
    name: 操作结果结点的名称
    """

    def __call__(self, input_nodes, name):
        pass

    """
    计算node结点的值
    node: 操作结果结点
    input_vals: 输入结点的值，与node.input_nodes是一一对应的
    """

    def compute(self, node, input_vals: List) -> np.ndarray:
        pass

    """
    计算node.input_nodes的jacobian向量积/梯度, dz/dX
    output_grad: dz/dY
    node：操作结果结点，即Y结点
    """

    def gradient(self, output_grad, node) -> List:
        pass


# 结点
class Node(object):

    # 构造器，主程序不使用这个构造器
    def __init__(self):
        self.input_nodes: List[Node] = []
        self.op: Operation = None
        self.name: str = ""

    def set_name(self, name: str):
        self.name = name

    def get_name(self) -> str:
        return self.name

    # 构造器，主程序只使用这个带参构造器
    @classmethod
    def instance(cls, input_nodes: List, op: Operation, name: str):
        node = cls()
        node.input_nodes = input_nodes
        node.op = op
        node.name = name
        return node

    """
    重写结点类的+-*/，以及右+-*/
    """

    # self + other: 重写为AddOp操作, 且右+与左+一致
    def __add__(self, other):
        name = ""
        if isinstance(other, Node):
            return add_op([self, other], name)
        else:
            const_node = Constant(other, str(other))
            return add_op([self, const_node], name)
    __radd__ = __add__

    # self - other: 重写为SubOp操作
    def __sub__(self, other):
        name = ""
        if isinstance(other, Node):
            return sub_op([self, other], name)
        else:
            const_node = Constant(other, str(other))
            return sub_op([self, const_node], name)

    def __rsub__(self, other):
        name = ""
        const_node = Constant(other, str(other))
        return sub_op([const_node, self], name)

    # self * other: 重写为MulOp操作，且右*与左*一致
    def __mul__(self, other):
        name = ""
        if isinstance(other, Node):
            return mul_op([self, other], name)
        else:
            const_node = Constant(other, str(other))
            return mul_op([self, const_node], name)
    __rmul__ = __mul__

    # self / other: 重写为DivOp操作
    def __truediv__(self, other):
        name = ""
        if isinstance(other, Node):
            return div_op([self, other], name)
        else:
            const_node = Constant(other, str(other))
            return div_op([self, const_node], name)

    def __rtruediv__(self, other):
        name = ""
        const_node = Constant(other, str(other))
        return div_op([const_node, self], name)

    # 相反数
    def __neg__(self):
        name = ""
        return neg_op([self], name)

    # 计算结点值
    def compute_val(self, input_vals: List) -> np.ndarray:
        return self.op.compute(self, input_vals)


# 操作类1：占位符操作类
class PlaceHolderOp(Operation):
    # 所有自变量结点都通过Variable()方法来生成
    def __call__(self, input_nodes, name) -> Node:
        node = Node.instance(input_nodes, self, name)
        return node

    # 占位符的值从node2ValMap中获取
    def compute(self, node: Node, input_vals: List):
        pass

    # 自变量结点无输入结点，故不存在输入结点梯度
    def gradient(self, output_grad, node):
        return None


# 产生自变量结点
def Variable(name: str) -> Node:
    node = place_holder_op([], name)
    return node


# 操作类2：常量操作类
class ConstOp(Operation):
    # 为保持方法签名的一致性，const不放在这个方法的入参中设置
    # 所有常量结点都通过Constant()方法来生成
    def __call__(self, input_nodes, name) -> Node:
        node = Node.instance([], self, name)
        return node

    def compute(self, node, input_vals: List):
        return node.const

    # 常量结点没有输入结点，故不存在输入结点的梯度
    def gradient(self, output_grad, node):
        return None


# 产生常量结点
def Constant(const, name: str = "") -> Node:
    node = const_op([], name)
    node.const = const
    return node


# 操作类3：element-wise加法，只支持常量的broadcast，因为常量的梯度不会被使用
class AddOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List) -> np.ndarray:
        return input_vals[0] + input_vals[1]

    # node.input_nodes中可能有常量，尽管output_grad与常量不同维度，
    # 但因为常量的梯度不会被使用，所有还是直接返回output_grad
    def gradient(self, output_grad: Node, node: Node) -> List[Node]:
        return [output_grad, output_grad]


# 操作类4：相反数
class NegOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List) -> np.ndarray:
        return -input_vals[0]

    def gradient(self, output_grad, node) -> List[Node]:
        return [-output_grad]


# 操作类5：element-wise减法
class SubOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List):
        return input_vals[0] - input_vals[1]

    def gradient(self, output_grad, node) -> List[Node]:
        return [output_grad, -output_grad]


# 操作类6：element-wise乘法
class MulOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List) -> np.ndarray:
        return input_vals[0] * input_vals[1]

    def gradient(self, output_grad, node) -> List[Node]:
        node0 = node.input_nodes[0]
        node1 = node.input_nodes[1]
        return [output_grad * node1, output_grad * node0]


# 操作类7：element-wise除法
class DivOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List):
        return input_vals[0] / input_vals[1]

    def gradient(self, output_grad, node) -> List[Node]:
        node0 = node.input_nodes[0]
        node1 = node.input_nodes[1]
        return [output_grad / node1, -output_grad * node0 / (node1 * node1)]


# 操作类8：矩阵转置
class MatTransposeOp(Operation):

    def __call__(self, input_nodes, name=""):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List[np.ndarray]) -> np.ndarray:
        return np.transpose(input_vals[0])

    def gradient(self, output_grad: Node, node) -> List:
        return [transpose_op([output_grad])]


# 操作类9：矩阵乘
class MatMulOp(Operation):

    def __call__(self, input_nodes, name):
        node = Node.instance(input_nodes, self, name)
        return node

    def compute(self, node, input_vals: List) -> np.ndarray:
        mat_a = input_vals[0]
        mat_b = input_vals[1]
        return np.matmul(mat_a, mat_b)

    def gradient(self, output_grad, node) -> List:
        mat_a = node.input_nodes[0]
        mat_b = node.input_nodes[1]
        partial_a = output_grad * transpose_op(mat_b)
        partial_b = transpose_op(mat_a) * output_grad
        return [partial_a, partial_b]


# 操作类10：element-wise log
class LogOp(Operation):

    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    def compute(self, node, input_vals: List) -> np.ndarray:
        return np.log(input_vals[0])

    def gradient(self, output_grad, node) -> List:
        node0 = node.input_nodes[0]
        return [output_grad / node0]


def log(node: Node, name="") -> Node:
    return log_op([node], name)


# 操作类11：element-wise exp
class ExpOp(Operation):

    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    def compute(self, node, input_vals: List) -> np.ndarray:
        return np.exp(input_vals[0])

    def gradient(self, output_grad, node) -> List:
        node0 = node.input_nodes[0]
        return [output_grad * exp_op([node0], "")]


def exp(node: Node, name="") -> Node:
    return exp_op([node], name)


# 操作类12：同维零矩阵
class ZeroLikeOp(Operation):

    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    def compute(self, node, input_vals: List) -> np.ndarray:
        return np.zeros_like(input_vals[0])

    def gradient(self, output_grad, node) -> List:
        node0 = node.input_nodes[0]
        return [zero_like_op([node0], "")]


# 操作类13：同维1矩阵
class OneLikeOp(Operation):

    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    def compute(self, node, input_vals: List) -> np.ndarray:
        return np.ones_like(input_vals[0])

    def gradient(self, output_grad, node) -> List:
        node0 = node.input_nodes[0]
        return [zero_like_op([node0], "")]


# 操作类14：降维求和 reduce_sum, 输出总和
class ReduceSum(Operation):

    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    def compute(self, node, input_vals: List) -> np.ndarray:
        return np.sum(input_vals[0])

    def gradient(self, output_grad, node) -> List:
        node0 = node.input_nodes[0]
        return [output_grad * one_like_op([node0], "")]


def reduce_sum(node: Node, name="") -> Node:
    return reduce_sum_op([node], name)


# 操作类15：Jacobian向量积
# 上述的操作1~14的gradient()方法没有用到这个操作，因为它们用矩阵的运算就能计算梯度
# 但如果新增的操作类无法用矩阵简单地计算梯度时，就需要用到Jacobian向量积操作来计算梯度
class JacobianOp(Operation):

    # input_nodes[0]代表partial_z_to_Y
    # input_nodes[1:]代表partial_yj_to_X
    def __call__(self, input_nodes, name):
        return Node.instance(input_nodes, self, name)

    # partial_z_to_Y已被排成一个行向量，Yj排序方法是按照维度排序:
    # 假设Y的维度是(a,b,c), 则j的范围是[0, a*b*c)
    # partial_Y_to_X与Yj一一对应
    def compute(self, node, input_vals: List) -> np.ndarray:
        partial_z_to_Y = input_vals[0]
        partial_Y_to_X = input_vals[1:]
        n = len(partial_z_to_Y)
        s = np.array(0)
        for j in range(n):
            s += partial_z_to_Y[j] * partial_Y_to_X[j]
        return s

    # 不需要用到
    def gradient(self, output_grad, node) -> List:
        pass


# 各个操作类的实例
place_holder_op = PlaceHolderOp()
const_op = ConstOp()
add_op = AddOp()
neg_op = NegOp()
sub_op = SubOp()
mul_op = MulOp()
div_op = DivOp()
transpose_op = MatTransposeOp()
mat_mul_op = MatMulOp()
log_op = LogOp()
exp_op = ExpOp()
zero_like_op = ZeroLikeOp()
one_like_op = OneLikeOp()
reduce_sum_op = ReduceSum()
jacobian_op = JacobianOp()


# BP自动微分
def bp_diff(z: Node, node_list: List[Node]) -> List[Node]:
    dp = {z: Constant(1)}  # 记录表
    grad_node_list = []
    # 由于结点的属性记录了父结点input_nodes，没有记录它的子节点
    # 所以要先遍历图，把所有结点的子节点都找出来，并存储到map中
    node_to_son_map = find_son(z)
    for x in node_list:
        grad_x = build_grad(dp, node_to_son_map, x)
        grad_node_list.append(grad_x)
    return grad_node_list


def build_grad(dp: dict, node_to_son_map: dict, x: Node) -> Node:
    if x in dp:
        return dp[x]
    sons = node_to_son_map[x]
    if sons is None:
        # 与z结点无关的结点才会走入这个分支
        dp[x] = zero_like_op(x, "")
        return dp[x]

    jacobian_list = []
    for y in sons:
        # 计算每个子节点的jacobian向量积
        y_grad = build_grad(dp, node_to_son_map, y)
        # 以下两行可以优化为用map来存储jacobian_of_inputs，只计算一次jacobian_of_inputs
        jacobian_of_inputs = y.op.gradient(y_grad, y)
        x_idx = y.input_nodes.index(x)

        jacobian = jacobian_of_inputs[x_idx]
        jacobian_list.append(jacobian)
    # 将所有子结点的jacobian向量积加起来就是x结点的梯度
    dp[x] = sum_jacobian(jacobian_list)
    return dp[x]


# 各个结点的儿子结点
def find_son(root: Node) -> dict:
    son_map = dict()
    son_map[root] = []
    visited = set()
    dfs_find_son(root, visited, son_map)
    return son_map


def dfs_find_son(root: Node, visited: set, son_map: dict):
    if root in visited:
        return
    # 前序遍历
    visited.add(root)
    for parent in root.input_nodes:
        if parent not in son_map:
            son_map[parent] = [root]
        else:
            son_map[parent].append(root)
        dfs_find_son(parent, visited, son_map)


# 返回node_list的和结点
def sum_jacobian(node_list: List[Node]) -> Node:
    from operator import add
    from functools import reduce
    return reduce(add, node_list)


# 自动微分，迭代写法
def bp_diff_iter(z: Node, node_list: List[Node]) -> List[Node]:
    topo_order = reversed(find_topo_sort([z]))
    grad_table = {}  # 梯度表
    node_to_jacobians = {z: [Constant(1)]}  # 雅可比向量积
    for y in topo_order:
        grad_y = sum_jacobian(node_to_jacobians[y])
        grad_table[y] = grad_y
        # y的各个输入结点的jacobian向量积，与y。input_nodes是一一对应的
        jacobian_of_inputs = y.op.gradient(grad_y, y)
        for i in range(len(y.input_nodes)):
            x = y.input_nodes[i]
            grad_x = jacobian_of_inputs[i]
            if x not in node_to_jacobians:
                node_to_jacobians[x] = [grad_x]
            else:
                node_to_jacobians[x].append(grad_x)

    grad_node_list = [grad_table[node] for node in node_list]
    return grad_node_list


# 拓扑排序
def find_topo_sort(node_list: List[Node]) -> List[Node]:
    visited = set()
    topo_order = []
    for node in node_list:
        post_dfs(node, visited, topo_order)
    return topo_order


# 后序遍历获得拓扑排序
def post_dfs(root: Node, visited: set, topo_order: List[Node]):
    if root in visited:
        return
    visited.add(root)
    if isinstance(root.input_nodes, Node):
        print(1)

    for node in root.input_nodes:
        post_dfs(node, visited, topo_order)
    topo_order.append(root)


# 图计算引擎/执行器
class Executor:

    """
    初始化
    eval_node_list: 要计算的结点
    """
    def __init__(self, eval_node_list: List[Node] = None):
        if eval_node_list is None:
            eval_node_list = []
        self.eval_node_list = eval_node_list

    """
    执行一次计算图，把eval_node_list中的结点及其祖先结点的值计算出来
    feed_dict: 输入自变量结点的值
    """
    def run(self, feed_dict: dict) -> List[np.ndarray]:
        # 按照拓扑排序的顺序去求值，可以保证计算当前结点的值时，它的输入结点的值都是可用的
        topo_order = find_topo_sort(self.eval_node_list)

        # 初始化node2valMap，填充自变量结点的值
        node_2_val_map = dict(feed_dict)
        for node in topo_order:
            if node in node_2_val_map:
                # 算过就不必再算一次
                continue
            input_vals = [node_2_val_map[x] for x in node.input_nodes]
            node_2_val_map[node] = node.compute_val(input_vals)

        result = [node_2_val_map[x] for x in self.eval_node_list]
        return result