[人工智能]LSTM学习笔记（Pytorch实现）

LSTM学习笔记（Pytorch实现）

1. LSTM解决的问题：长程依赖问题

在传统的RNN中，梯度是会时间序列的向前而不断积累的

当梯度的绝对值小于1，在时间序列很长的情况下梯度最终会接近0，这种现象叫梯度消失（Vanishing Gradient Problem）

相反，当梯度的绝对值大于1，那么梯度最终会接近无穷大，这种现象叫梯度爆炸（Gradient Exploding Problem）

由于这两个问题，RNN很难建模长时间间隔状态之间的依赖关系，这个问题叫做长程依赖问题（Long-Term Dependencies）

2. LSTM的原理

引入门控机制来控制信息的积累速度，包括

• 输入门$i_t$：有选择的加入新信息
• 遗忘门$f_t$：有选择的的遗忘之前积累的信息
• 输出门$o_t$：有选择的输出信息给外部状态

LSTM（Long short-term memory）因而得名，被理解为长的短期记忆网络

注：“长”代表可以处理很长的序列，这表示LSTM可以消除长程依赖引发的问题，但并不表示该模型可以实现长程依赖（长距离的信息被“门”关掉了）

3. LSTM公式

传统RNN公式如下：
$$\begin{gathered} h_t=f(U{h}_{t?1}+W{x}_t+b) \\ {y}_t=V{h}_t \end{gathered}$$
其中$h$为隐状态，$f(?)$为激活函数，$U,W,b,V$为网络参数

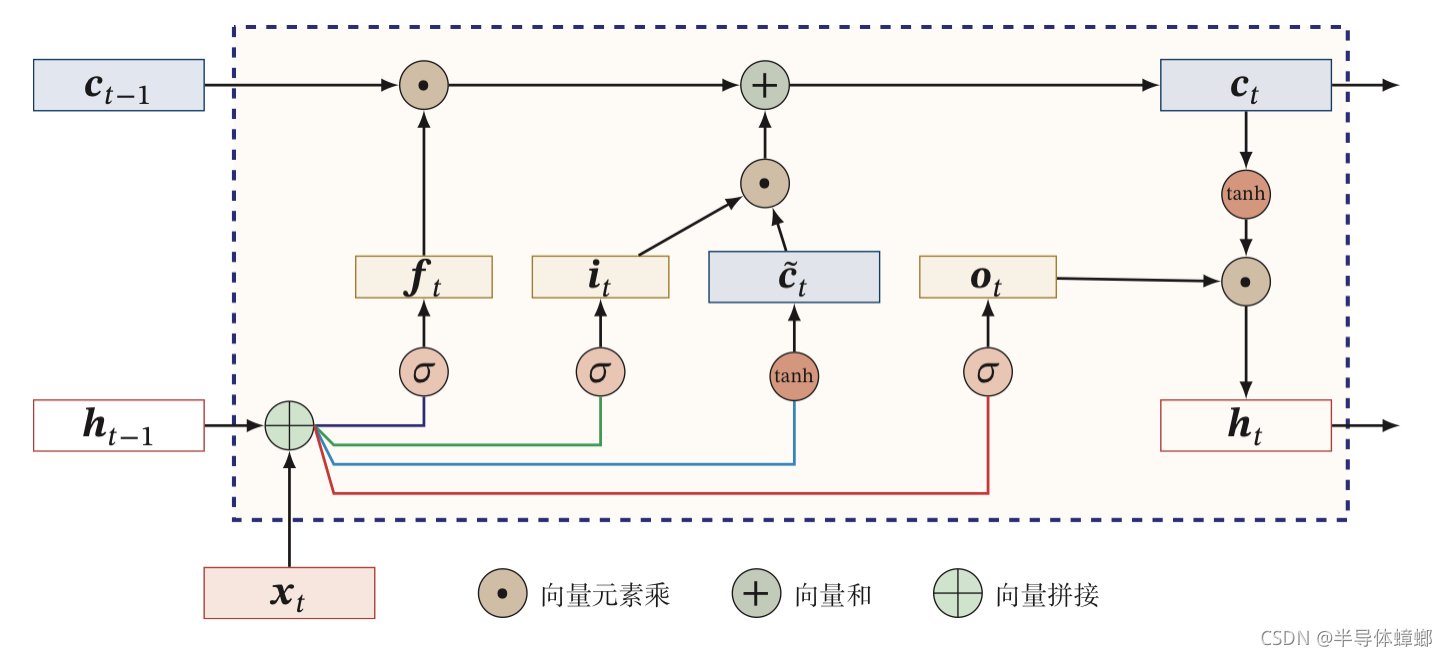
LSTM在此基础上引入了新的内部状态$c_t$专门进行线性的循环传递信息，同时非线性的输出信息给隐藏层的外部状态$h_t$,一个单元的运算流程如图所示：

首先利用上一时刻的外部状态$h_{t?1}$和当前的输入$x_t$计算出三个门，以及候选状态$c_t$
$$\begin{gathered} i_t=\sigma (W_i{x}_t+U_i{h}_{t?1}+b_i) \\ {f}_t=\sigma (W_f{x}_t+U_f{h}_{t?1}+b_f) \\ {o}_t=\sigma (W_o{x}_t+U_o{h}_{t?1}+b_o) \\ 其中\sigma (?)为sigmoid函数 \\ {c}_t=tanh(W_c{x}_t+U_c{h}_{t?1}+b_c) \end{gathered}$$
这四个公式可以用一个式子来描述：
$$?\begin{array}{c}{i}_t\\ f_t\\ o_t\\ c_t\end{array}?=?\begin{array}{c}\sigma \\ \sigma \\ \sigma \\ tanh\end{array}?(W\left[\begin{array}{c}{x}_t\\ h_{t?1}\end{array}\right]+b)\text{\hspace{1em}(1)}$$
之后结合遗忘门$f_t$和输出门$i_t$来更新记忆单元$c_t$
$$c_t=f_t\odot c_{t?1}+i_t\odot c_t\text{\hspace{1em}(2)}$$
最后结合输出门$o_t$，将内部状态的信息传递给外部状态$h_t$
$$h_t=o_t\odot tanh(c_t)\text{\hspace{1em}(3)}$$

4. 实现LSTM单元

4.1 模型初始化

为了加快计算，采用公式2的方式计算，但W有所变化

• 由于x与h的维度不一样，一次需要将W分成W和U分别算x的隐层输出和h的隐层输出

• 由于激活函数不一样，并且更新h和c需要的参数需要将结果分开，因此这里的W和U需要自定义参数（使用nn.Parameter，而不是nn.Linner）

因此初始化代码如下：

#embedding_dim:x的embeding维度；hidden_dim:隐藏层维度
self.W = nn.Parameter(torch.Tensor(embedding_dim, hidden_dim * 4))
self.U = nn.Parameter(torch.Tensor(hidden_dim, hidden_dim * 4))
self.bias = nn.Parameter(torch.Tensor(hidden_dim * 4))
# 由于Parameter参数初始化为0，需要手动参数初始化
standard_value = 1.0 / math.sqrt(self.hidden_dim)
for weight in self.parameters():
    weight.data.uniform_(-standard_value, standard_value)

4.2 forward

输入：$x_t，h_{t?1}，c_{t?1}$

输出：$h_t，c_t$

为了加快计算，$x_t$是以batch的形式出现的，他表示当前的batch当前第i个序列的所有单词，所以维度为：batch_size*embedding_dim，并且对不同的x序列会产生不同的h的c，因此h和c的batch_size与x相同，维度为：batch_size*hidden_dim

这样，参数的维度就确立了

def forward(self, x, h, c):pass
    """
    :param x: batch_size*embedding_dim
    :param h: batch_size*hidden_dim  对于不同的batch，h的参数是不同的
    :param c: batch_size*hidden_dim
    :return: h,c: batch_size*hidden_dim
    """

细节：forward处理可变长x的计算方式

由于句子是不定长的，因此输入x中的batch_size是不固定的，如图所示

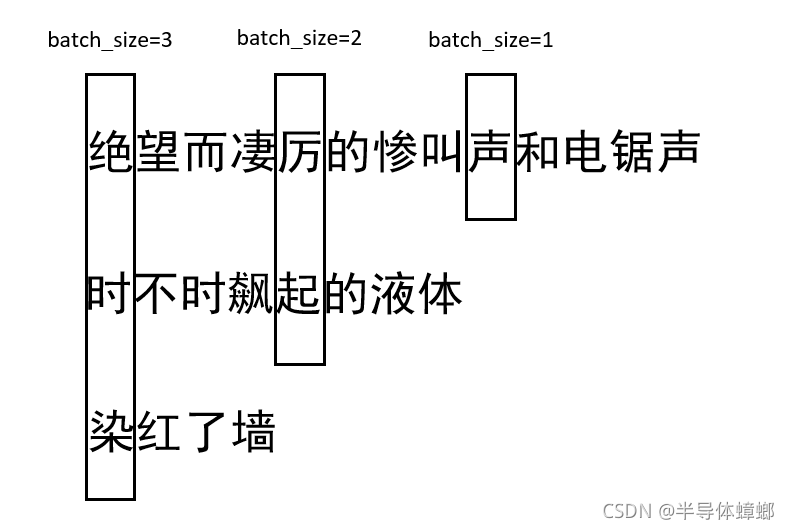
这导致了上一时间序列的h，c的batch_size也是不固定的，因此需要对bias进行动态的扩展维度以适应计算

# 对bias进行维度扩展，以适应batch_size
bias=self.bias.unsqueeze(0).expand(x.size(0),-1)

剩下的过程照着公式写就ok了，代码如下：（c_temp表示$c_t$）

hidden_state = torch.mm(x, self.W) + torch.mm(h, self.U) + bias # hidden_state : batch_size*(hidden_dim*4)
c_temp, o, i, f = hidden_state.split(self.hidden_dim, dim=1)
c_temp, o, i, f = torch.tanh(c_temp), torch.sigmoid(o), torch.sigmoid(i), torch.sigmoid(f)
c = f * c + i * c_temp
h = o * torch.tanh(c)

4.3 LSTM单元全部代码

import torch
import math
from torch import nn
class LSTMCell(nn.Module):
    """
    序列在LSTM单元的一次传播
    """
    def __init__(self, embedding_dim, hidden_dim):
        super().__init__()
        self.hidden_dim = hidden_dim
        self.W = nn.Parameter(torch.Tensor(embedding_dim, hidden_dim * 4))
        self.U = nn.Parameter(torch.Tensor(hidden_dim, hidden_dim * 4))
        self.bias = nn.Parameter(torch.Tensor(hidden_dim * 4))
        # 由于Parameter参数初始化为0，需要手动参数初始化
        standard_value = 1.0 / math.sqrt(self.hidden_dim)
        for weight in self.parameters():
            weight.data.uniform_(-standard_value, standard_value)
    def forward(self, x, hidden):
        """
        :param x: max_batch_size*embedding_dim
        :param h: batch_size*hidden_dim  对于不同的batch，h的参数是不同的
        :param c: batch_size*hidden_dim
        :return: h,c: batch_size*hidden_dim
        """
        h,c=hidden
        # 对bias进行维度扩展，以适应batch_size
        bias=self.bias.unsqueeze(0).expand(h.size(0),-1)
   	    # hidden_state : batch_size*(hidden_dim*4)
        hidden_state = torch.mm(x, self.W) + torch.mm(h, self.U) + bias
        c_temp, o, i, f = hidden_state.split(self.hidden_dim, dim=1)
        c_temp, o, i, f = torch.tanh(c_temp), torch.sigmoid(o), torch.sigmoid(i), torch.sigmoid(f)
        c = f * c + i * c_temp
        h = o * torch.tanh(c)
        return h, c

5. 基于LSTM单元实现整个LSTM序列向前传播的算法

5.1 pack_padded_sequence

为了处理可变长序列即让x，h和c的batch_size能够随着时间序列变化而变化进而送进LSTM单元计算，我们需要对原始输入序列x进行处理，torch中提供了pack_padded_sequence方法用来处理原始输入序列，示例如下：

a1 = torch.tensor([1, 2, 3, 5, 4]) # sentence 1
a2 = torch.tensor([5, 6, 7]) # sentence 2
a3 = torch.tensor([7, 8]) # sentence 3
a4 = torch.tensor([7]) # sentence 3
train_x = [a1, a2, a3, a4] #tensor列表，用来表示每个句子
seq_len = [s.size(0) for s in train_x] #保存每个句子的长度
data = pad_sequence(train_x, batch_first=True) #将tensor列表padding，变成tensor矩阵
print(data)
data2 = pack_padded_sequence(data, seq_len, batch_first=True) #执行pack_padded_sequence
print(data2.data)
x=data2.data
batch_sizes=data2.batch_sizes.tolist()
print(torch.split(x,batch_sizes))

#结果
data
tensor([[1, 2, 3, 5, 4],
        [5, 6, 7, 0, 0],
        [7, 8, 0, 0, 0],
        [7, 0, 0, 0, 0]])
data2.data
tensor([1, 5, 7, 7, 2, 6, 8, 3, 7, 5, 4])
torch.split(x,batch_sizes)
(tensor([1, 5, 7, 7]), tensor([2, 6, 8]), tensor([3, 7]), tensor([5]), tensor([4]))

pack_padded_sequence接收很多句子组成的tensor矩阵，和每个句子长度而组成的列表

进而生成一个长度为sum(seq_len)的向量和每个时刻的有效batch组成的列表，并将两者打包到一个变量中

之后用torch.split()方法就能变成随着时间序列有不同的batch的输入

这里文字叙述太繁琐，上图

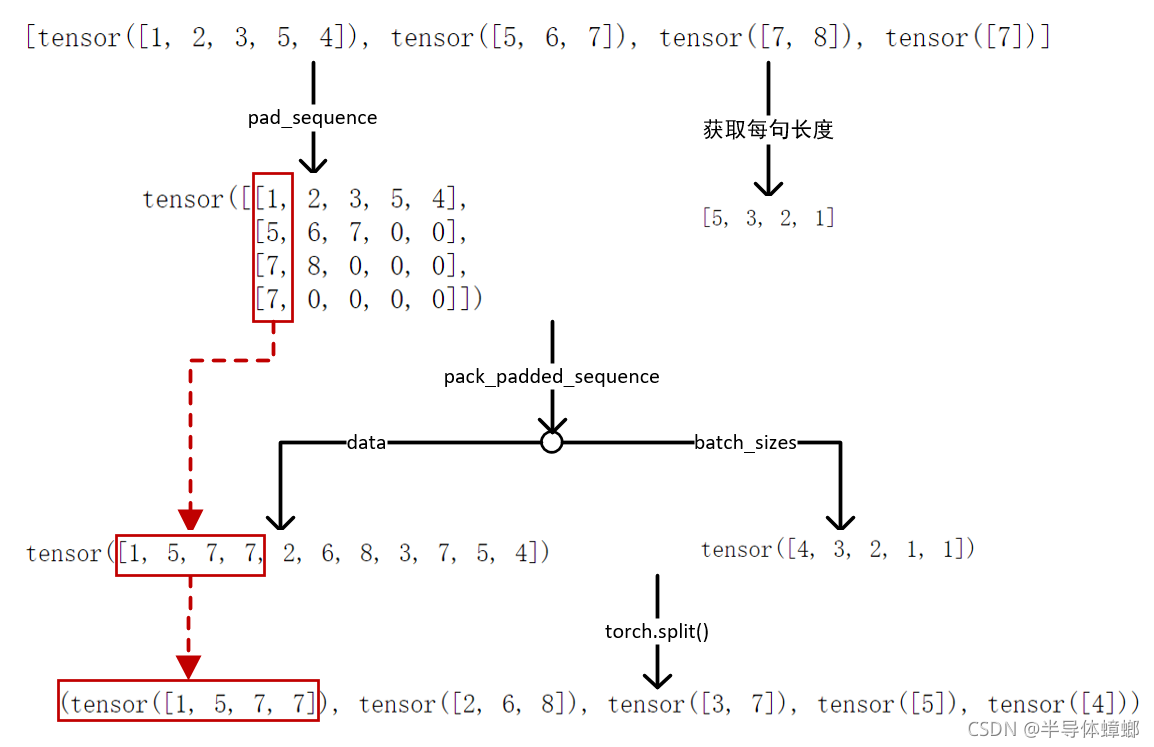
由于pack_padded_sequence输入的是句子长度的列表，因此为了得到有效的batch，句子长度的列表必须是由高到低排序的，否则不知道该选取batch中的哪一个有效的句子作为输入

5.2 模型初始化

这里只用到了LSTM单元，但是由于参数量过多，为了减少模型的过拟合，一般会在模型的末尾添加Dropout，初始化关键代码如下：

self.dropout = nn.Dropout(dropout_rate)
self.lstmcell=LSTMCell(embedding_dim, hidden_dim)

5.3 forward

首先确定forward的输入和输出

5.3.1 输入的形式

如上图所示，输入可以是第三个也可以是最后一个，为了简洁或统一代码的编写，一般采用第三个，即将pack_padded_sequence的结果作为输入

pack_padded_sequence的结果是一个类似元组的性质，里面的数据不能被更改，因此如果在第三步之后要添加embedding层的话，要将pack_padded_sequence的结果分开在计算，在输入给LSTM，这样LSTM就会有两个参数，即embedding后的data和batch_sizes

所以输入有两种变化

def forward(self, x, batch_sizes):pass #将data与batch_sizes分开
def forward(self,sequence):
    x=sequence.data
    batch_sizes=sequence.batch_sizes
    pass

5.3.2 输出 $h_t$和$h_n$的形式

考虑不同的任务，LSTM的输出有两种：

• 每一个时间序列 t 的隐含状态$h_t$，该输出可以用于序列标注或生成等任务
• 最后一时间序列的隐含状态$h_n$，该输出可以用于句子级别标注的任务

模型要求输出每一个时间序列 t 的隐含状态$h_t$，但是每一个时间序列的batch不一样，这也导致了$h_t$的维度不一样，若用列表存储的话会有点麻烦，这里采用了与pack_padded_sequence的结果相同的形式，将每一个时间步的结果拼接起来形成一个矩阵，矩阵的每一行对应输入的data

$h_n$也同样符合这个情况，当第i个句子结束时，$h_n$即为最终状态，不需要再更新，即将$h_n(i)$保持在当前状态即可

整体的流程如图所示（最大句长为5，最大batch为5）（joint表示拼接，即torch.cat()）

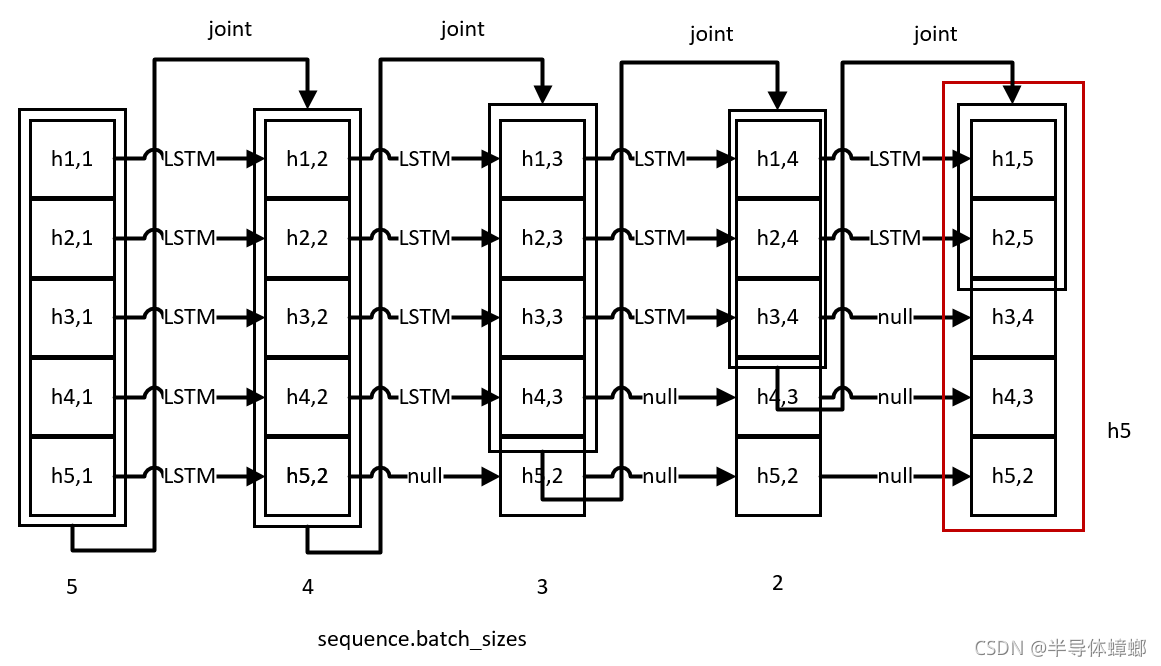
输出维度如下：

:return h_t: embedding_dim*sum(batch_sizes)
    	h_n: max_batch_sizes*hidden_dim

由于输入形式不一样，此过程可以设立一个单独的函数来解决用来适配不同的输入，实现的代码如下：

def layer_forward(self, x, h, c, cell, batch_sizes):
    """
        :param x: sentence_len*batch_size*embedding_dim
        :param h: batch_size*hidden_dim 初始的h0
        :param c: batch_size*hidden_dim 初始的c0
        :param cell: LSTMCell模型
        :param batch_sizes: sentence_len，一个batch中大于等于当前句子长度的数量
        :return: h_t：列表，全部状态
        		h_n,最后一个状态
        """
    h_n=[]
    h_t = []
    for t in range(len(x)):
        last_batch_size, batch_size = len(h), batch_sizes[t]
        if last_batch_size > batch_size:
            h_n.append(h[batch_size - last_batch_size:])
        h = h[:batch_sizes[t]]
        c = c[:batch_sizes[t]]
        h, c = cell(x[t], h, c)
        h_t.append(h)
return h_t, h_n #注：h_t为列表，需要再使用torch.cat(h_t)拼接成矩阵

5.4 初始化$h_0，c_0$

根据公式，无论$h_0，c_0$初始化成什么值，只要在训练和测试还有开发都是一样的，那么就能够保持模型的正确性，这里让其都初始化为0

init = x.new_zeros(max_batch_size, self.hidden_size) #new_zeros:生成新的矩阵
h,c=(init,init)

这样，所有细节都已完成，最终代码如下：

5.5 LSTM全部代码

import torch
import torch.nn as nn
from LSTMCell import LSTMCell
from torch.nn.utils.rnn import PackedSequence
class SimpleLSTM(nn.Module):
    """
    简单的LSTM，没有双向，只有一层
    """
    def __init__(self, hidden_dim, embedding_dim, dropout_rate=0.1):
        super().__init__()
        self.dropout = nn.Dropout(dropout_rate)
        self.cell=LSTMCell(embedding_dim,hidden_dim)

    def forward(self, x, batch_sizes): #这里采用了第二种输入，用来适配embedding_dim
        """
        :param sequence: batch_size*sentence_len*embedding_dim
        :return: h,n : batch_size*sentence_len*hidden_dim
        """
        batch_sizes_temp=batch_sizes
        batch_sizes = batch_sizes.tolist()
        max_batch_size = batch_sizes[0]
        init=x.new_zeros(max_batch_size,self.hidden_dim)
        h,c=init,init
        x = torch.split(x, batch_sizes) #注:x此时为不定长tensor列表
        h_t,h_n=self.layer_forward(x, h, c, self.cell, batch_sizes)
        h_t=torch.cat(h_t)
        h_t=self.dropout(h_t)
        # h_t=PackedSequence(h_t,batch_sizes_temp) 需要pack回来会话写这一步
        return h_t,h_n

    def layer_forward(self, x, h, c, cell, batch_sizes):
        """
        每一层，单向的forward
        :param x: sentence_len*batch_size*embedding_dim
        :param h: batch_size*hidden_dim
        :param c: batch_size*hidden_dim
        :param cell: LSTMCell模型
        :param batch_sizes: sentence_len，一个batch中大于等于当前句子长度的数量
        :return: h_n,最后一个状态，h_t：列表，全部状态
        """
        h_n=[]
        h_t = []
        for t in range(len(x)):
            last_batch_size, batch_size = len(h), batch_sizes[t]
            if last_batch_size > batch_size:
                h_n.append(h[batch_size - last_batch_size:])
            h = h[:batch_sizes[t]]
            c = c[:batch_sizes[t]]
            h, c = cell(x[t], h, c)
            h_t.append(h)
        return h_t, h_n

6. 应用LSTM解决序列标注问题

应用步骤即将h_t再加入一个线性层映射到标注的类别，此外再之前添加一个embedding层（如果需要的话）即可，代码如下：

import torch.nn as nn
from LSTM import LSTM
class SimpleLSTMTagger(nn.Module):
    def __init__(self,config):
        super().__init__()
        self.embedding=nn.Embedding(config.vocab_size,config.embedding_dim)
        self.embedding_dropout=nn.Dropout(config.dropout_rate)
        self.lstm=LSTM(config.embedding_dim, config.hidden_dim)
        output_hidden_dim=config.hidden_dim if config.bidirectional==False else config.hidden_dim*2
        self.output_layer = nn.Linear(output_hidden_dim, config.tag_num)

    def forward(self,x):
        """
        :param x: pack_padded_sequence
        :param batch_sizes: sentence_len of every batch
        :return: embedding_dim*sum(sentence_len)
        """
        embedding_output=self.embedding(x.data)
        embedding_output=self.embedding_dropout(embedding_output)
        x , _=self.lstm(embedding_output,x.batch_sizes)
        x=self.output_layer(x.data)
        return x

技巧：输出不用pack，这样x与y_hat都是一维的，在训练中计算loss不需要复杂的操作，代码如下：

#训练关键代码
for x, y, batch_len in tqdm(dataloader, desc="{}/{} train epoch:".format(epoch + 1, config.epochs)):
    x , y = x.to(device) , y.to(device)
    batch_len = torch.sort(batch_len, descending=True)
    x , y = x[batch_len.indices] , y[batch_len.indices]
    x = pack_padded_sequence(x, batch_len.values, batch_first=True)
    y = pack_padded_sequence(y, batch_len.values, batch_first=True).data
    y_hat = lstm(x)
    loss = nn.CrossEntropyLoss(y_hat, y) #计算loss只要这一行即可
    total_loss += loss.item()
    loss.backward()
    optimizer.step()
    lstm.zero_grad()

7. 多层、双向LSTM

多层即将上一层的$h_t$作为输入到下一层产另一个$h_t$，双向即将两个方向得到的$h_t$结果进行拼接得到新的$h_t$（$h_n$也一样）

初始化代码：

for layer in range(self.num_layers):
    for direction in range(self.num_directions):
        if layer == 0:
            cell = LSTMCell(self.input_size, self.hidden_size)
            else:
                cell = LSTMCell(self.hidden_size, self.hidden_size)
                setattr(self, 'cell_{}_{}'.format(layer, direction), cell)

forward关键代码：

for layer in range(self.num_layers):
    for direction in range(self.num_directions):
        if direction == 0:
            f_output, (h_n, c_n) = self.layer_forward(x=f_output, #将上一层的h_t作为输入到下一层产另一个h_t
                                                      hx=hx,
                                                      cell=self.get_cell(
                                                          layer, direction),
                                                      batch_sizes=batch_sizes,
                                                      reverse=False)
            hn.append(h_n)
            cn.append(c_n)
            else:
                b_output, (h_n, c_n) = self.layer_forward(x=b_output,
                                                          hx=hx,
                                                          cell=self.get_cell(
                                                              layer, direction),
                                                          batch_sizes=batch_sizes,
                                                          reverse=True)
                hn.append(h_n)
                cn.append(c_n)
f_output, b_output = torch.cat(f_output), torch.cat(b_output)
hn, cn = torch.cat(hn, 0), torch.cat(cn, 0)
output = torch.cat([f_output, b_output], -1) #双向拼接

此外，需要编写的还有反向的LSTM，该过程不仅要将时间步调过来，而且batch_size从由大变小变成由小变大，计算过程需要调整，代码如下

def layer_forward(self, x, hx, cell, batch_sizes, reverse=False):
     h, c = hx
     init_h, init_c = h, c
     output, seq_len = [], len(x)
     h_n, c_n = [], []
     steps = reversed(range(seq_len)) if reverse else range(seq_len)
     for t in steps:
         last_batch_size, batch_size = len(h), batch_sizes[t]
         if last_batch_size < batch_size:
             h = torch.cat((h, init_h[last_batch_size:batch_size]))
             c = torch.cat((c, init_c[last_batch_size:batch_size]))
         else:
             if not reverse:
                 if last_batch_size > batch_size:
                     h_n.append(h[batch_size - last_batch_size:])
                     c_n.append(c[batch_size - last_batch_size:])
             h = h[:batch_size]
             c = c[:batch_size]
         h, c = cell(x[t], (h, c))
         output.append(h)
     if not reverse:
         h_n.append(h)
         c_n.append(c)
     if reverse:
         output.reverse()
         h_n.append(h)
         c_n.append(c)
     return output, (torch.cat(h_n).unsqueeze(0), torch.cat(c_n).unsqueeze(0))