# 4.1

setwd('file path')
library(tseries)
library(xlsx)
library(ggplot2)
library(forecast)
library(fpp2)
library(aTSA)

# 绘制该序列时序图 ----------------------------------------------------------------

data4_1 <- read.xlsx('E4_1.xlsx', sheetIndex = 1)
ts.plot(data4_1$x)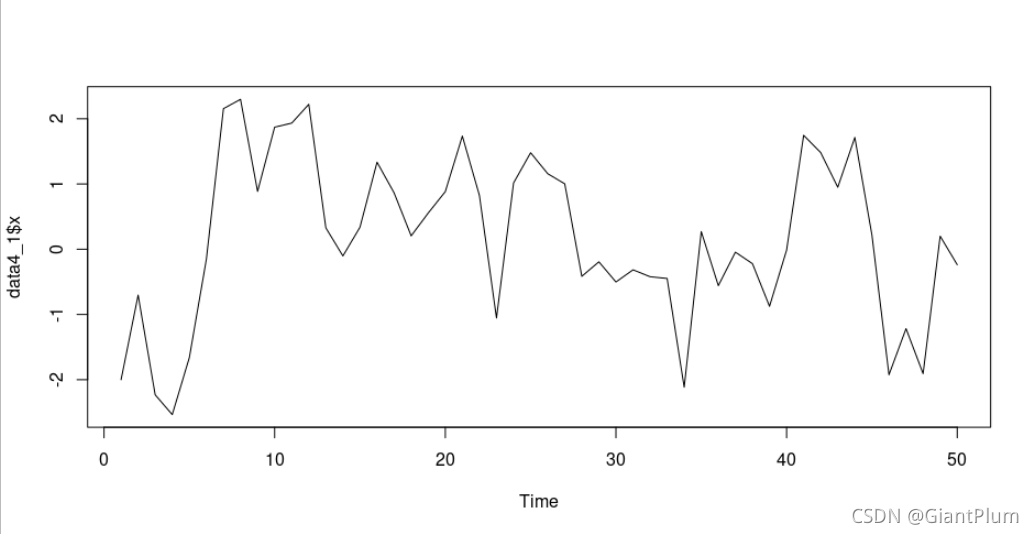

# 判断平稳性和纯随机性 --------------------------------------------------------------

adf.test(data4_1$x)

	Augmented Dickey-Fuller Test

data:  data4_1$x
Dickey-Fuller = -3.9427, Lag order = 3, p-value = 0.01919
alternative hypothesis: stationary

由于单位根检验p<0.05, 故认为该序列平稳。

Box.test(data4_1$x)

	Box-Pierce test

data:  data4_1$x
X-squared = 17.331, df = 1, p-value = 3.14e-05

由于LB检验p<0.05, 故认为该序列为非白噪声序列。

# 根据acf和pacf进行模型识别 --------------------------------------------------------

acf(data4_1$x)
pacf(data4_1$x)

?由图可见ACF拖尾， PACF 1阶截尾。

# 建立模型 --------------------------------------------------------------------

fit4_1 <- arima(data4_1$x, order = c(1, 0, 0), method = "ML")

# 模型检验 --------------------------------------------------------------------

for (i in 1:4) {
    print(Box.test(fit4_1$residual, lag = 4*i, type = "Ljung-Box"))
}
	Box-Ljung test

data:  fit4_1$residual
X-squared = 0.49319, df = 4, p-value = 0.9742
	Box-Ljung test

data:  fit4_1$residual
X-squared = 6.7532, df = 8, p-value = 0.5635
	Box-Ljung test

data:  fit4_1$residual
X-squared = 7.5201, df = 12, p-value = 0.8214
	Box-Ljung test

data:  fit4_1$residual
X-squared = 12.227, df = 16, p-value = 0.7282

由于残差的各阶纯随机检验均p>0.05, 故认为残差序列已实现白噪声。

t <- abs(fit4_1$coef) / sqrt(diag(fit4_1$var.coef))
pt(t, length(data4_1$x) - length(fit4_1$coef), lower.tail = F)

ar1	intercept
9.258397e-07	4.119551e-01

?由于 $\phi _{1}$ 的p值小于0.05，故认为 $\phi _{1}$ 显著不为零。

ts.diag(fit4_1, lag.seq = 1:12)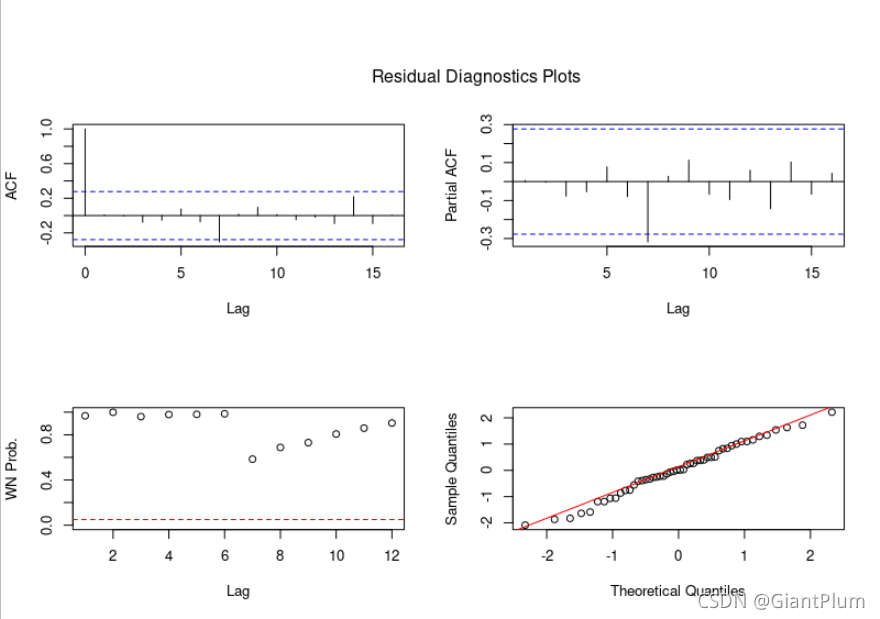

?由残差的ACF、PACF、QQ和白噪声概率图可知残差已为白噪声，故认为AR(1)模型是该序列的有效拟合模型。

模型表达式： $(1 - 0.6144B)x_{t} = 0.0799 + \varepsilon _{t}$

# 模型预测 --------------------------------------------------------------------

h <- 5    # 预测期数

fore4_1 <- forecast::forecast(fit4_1, h = h)
plot(fore4_1, xlab = "Time", ylab = "公司盈亏（万元）")

q <- qnorm(0.975, 0, 1)

L1 = fore4_1$fitted - q*sqrt(fit4_1$sigma2)
U1 = fore4_1$fitted + q*sqrt(fit4_1$sigma2)

L2 = fore4_1$lower[, 2]
U2 = fore4_1$upper[, 2]

L <- c(L1, L2)
U <- c(U1, U2)

c1 = min(data4_1$x, L)
c2 = max(data4_1$x, U)

fitted_and_mean <- c(fore4_1$fitted , fore4_1$mean)

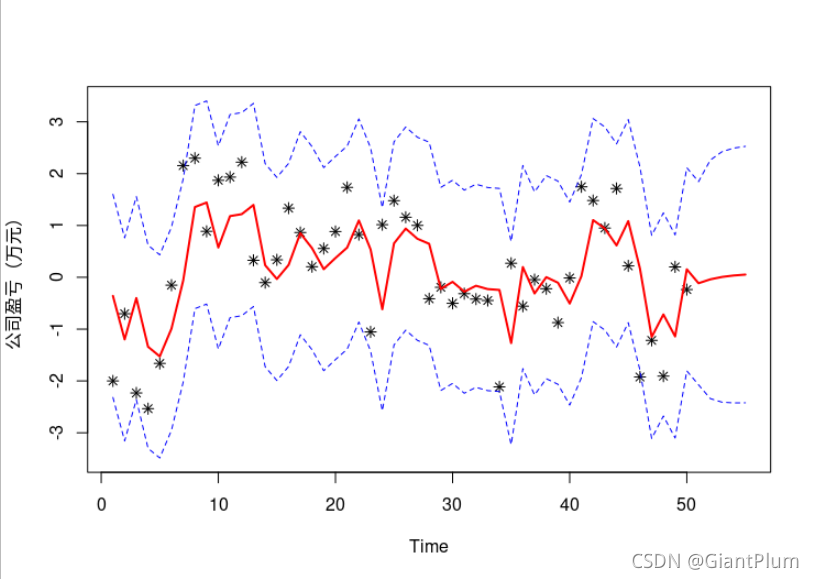
plot(data4_1$x, type = "p", pch = 8, ylim = c(c1, c2), xlab = "Time",
     xlim = c(min(data4_1$t), max(data4_1$t) + h), ylab = "公司盈亏（万元）")
lines(fitted_and_mean, col = 2, lwd = 2)
lines(L, col = 4, lty = 2)
lines(U, col = 4, lty = 2)