[人工智能] 基于ROS 履带车从零开始制做（2）：科普人工智能，无人驾驶

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 基于ROS 履带车从零开始制做（2）：科普人工智能，无人驾驶 -> 正文阅读

[人工智能]基于ROS 履带车从零开始制做（2）：科普人工智能，无人驾驶

人工智能

历史

推荐电影：《模仿游戏》 --讲的是图灵机的诞生

第一次低谷1974 - 1980：

计算机的运算能力
计算复杂性和指数爆炸
常识与推理（训练数据集）
。证明定理和解决几何问题对计算机而言相对容易，而一些看似简单的任务，如人脸识别或穿过屋子，实现起来却极端困难。这也是70年代中期机器视觉和机器人方面进展缓慢的原因

第二次AI低谷：1987 - 1993：

专家系统维护费用居高不下。它们难以升级，难以使用，脆弱（当输入异常时会出现莫名其妙的错误），成了以前已经暴露的各种各样的问题（例如资格问题（qualification problem））的牺牲品。专家系统的实用性仅仅局限于某些特定情景。[121]

里程碑1997：“深蓝”打败象棋冠军

大爆发2006：深度学习

机器学习的处理的问题

监督：是否需要训练数据支撑，训练数据示例 [身高：175 ，体重：60kg , 结论：标准] ，其中身高和体重是模型的输入，结论是模型的输出，训练数据是人工标定的，模型通过多组训练数据进行参数动态调整。

常见的机器学习算法

为什么机器学习执着于解决回归和分类问题，而且主要是分类问题？

非此即彼也许可以解释这个，日常生活中的决策都是分类问题，无非是种类的多少。比如“围棋对战中”也可以表示为分类问题：棋盘上剩余的空点都可以下棋，输出也就可以分成这么多类，具体选哪一类呢？根据当前棋盘的落子情况和规则，推理出每个落点”代价“ ，再继续往后推理，当前每个点落子后，下一轮的代价，如此反复，计算机能得到每一步棋很深的一个预测，而围棋高手之所有称为高手，就是应为有大局观，能够进行深层次的布局。显然，在有限的时间内，计算机的考虑更全面（在强大算力前提下），布局也更深。

回归问题

线性回归

如下图所示，通过采集数据，得到了web网站的点击量与广告费关系图，根据这张图，我们能得到广告费为200w的点击量吗？

?回归问题：通过已经产生的数据，对未产生的数据进行预测，说白了就是通过数据求数据之间的关系（方程），再通过方程，在已知某一个数据得情况下，预测另一个数据。

根据图中得点，我们大概能画出这样的一条直线，我们期望的是所有点尽可能均匀分布在直线两侧。那么，在已知所有的样本点的情况下，如何求这条完美直线呢？

? ? ? ? ? ? ? ? ? ?

最小二乘法

思路：

我们通过观察数据，觉得它挺符合一次函数的，那不妨设一次函数为 ?
目标是让点尽可能靠近直线，这句话翻译过来就是点离直线尽可能的近 , 假设第一个点为 ?，也就是误差

? 值足够小，这里取平方，消去绝对值符号便于计算（不用分段），这里我们称之为误差的平方，也是二乘的由来

?要让所有的点尽可能靠近，也就是所有点的误差之和最小。规范一下命名，就得到以下误差总和函数，也称为代价函数

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ? ? ? ? ? ?

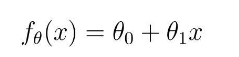
现在只需要求得，? 和 ? 使得 E（?）最小。 E 是关于 ? 的二次函数，可以通过求导得到极值，导数（斜率）为0。
单自变量求导容易，如下图

? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

?本例中为两个变量，回归方程不使用一次函数，变量将更多，多变量通过求偏导得到极值。

? ? ? ? ? ?

? ? ? ? ? ?如果误差总和函数不是二次函数，而是更加复杂的函数呢？比如下面的图形，如何求最小值？它的函数可能是：

它的图像可能是这种：

?显然，通过导数等于零的方法求极值变得难度极大，这个计算量也是导致神经网络第一次萧条的原因。如果通过更复杂的函数作为回归函数，比如多元多次，多项式，那么求导将变得无比复杂，有没有比求导更好的方法呢？梯度下降解决了这个问题。目前只需要知道，梯度下降只是为了解决复杂的求导问题。

梯度下降：复杂函数求极值

寻找下山的路：在任何一个地方，都寻找地势最低的地方走，假如你像孙猴子一样有无数个分身，从山顶不同的位置出发，当所有分身都找到个无法在下降的点时，比较所有点的地势，找出最低的点（防止你在某个山沟，却认为到了山下）就是基本确认到达山底。

梯度下降的数学表示方法：

单变量与多变量的近似公式
- 单变量的近似公式

? ? ??

???多变量的近似公式（具体见泰勒展开式）

? ? ? ? ??

近似公式的向量表示方法 ????????
向量内积的特点

? 根据柯西-施瓦茨不等式：

?将上述结论运用到由近视公式的向量表示法

? 要想 ? 取得最小值（? 越小，表明每次下降越快），则需要满足 ? , 图像表示出来就是 a，b向量相反

根据上面这个公式，我们就知道如何调整我们的坐标 x ,y . 举例，在（x =1 , y =3）点处，如何决定下一步往哪走？，分别求出

????????????????y = 3 时， f(x ,3) 对 x的偏导

????????????????x= 1 时， f(1，y) 对 y的偏导

????????????????n 称为学习率，为常数

????????????????后面的部分称为梯度

思考：这种走一步看一步的方法真能找到最小值吗？

随机梯度下降法：解决局部最优解问题

局部最优解：

? ? ? ? ? ??

重新整理一下整个过程：

定义输入与输出的关系式，也就是模型 f(x) , 线性回归的例子是 ?
定义代价函数（误差函数），? ，所有样本（训练数据）的误差和
求代价函数的最小值，求导太复杂，使用梯度下降，走一步看一步
解决局部最优解的问题
- 选用合适的学习率，过小无法逃脱，过大会在最小值附近震荡。

选用不同的起点

拿一开始的广告费预测为例

假设? 为0 , 我们只考虑一个参数的情况，则代价函数是关于 ?的一元二次方程，采用梯度下降，初始 ?可能是下图位置，当训练完成，陷入局部最优解。 ?

当上图现象出现，需要重新设置?的值，然后重新训练模型，直到出现下图的 ? 值，由于训练耗时，而且难以评估是否陷入局部最优解，因此，使用所有的训练数据形成的代价函数不可取。

? 将训练集分成不同批次，比如训练数据由有10w个 , 将其分成100组，每组数据都是随机选取，这样得到了100个训练集，就相当于从100个点出发，虽然每组的数量减少了，但是由于有 100 个随机的出发点，自然找到最下值得概率大大增加。

分类问题

最简单的分类方法：分段函数

感知机

向量的内积理解感知机
- 向量定义的扩展：由有方向和大小的量(力，速度) 扩展为不同维度的变量，如（身高，体重）属于不同维度的变量，他们组成的数集表示成一个二维向量。
- 向量内积的几何意义 : 向量的相似性

?向量内积的坐标表示

证明方法：

?

有了上面的基础，再来理解感知机：感知机的结果为权重向量 w 和输入向量x 的内积，从几何意义来看，内积的结果反应了向量w 和 x 的相似程度，到底有多相似呢，因为向量大小不同，不同的系统无法通过内积的结果评判相似程度，我们希望能更好的描述相似程度，最好通过概率的形式，比如 90% 的相似。如何做到呢？ ?

? ? ? ? ? ?

第一步，我们应该将输入 ? 进行归一化， ?... ，这要样不同组的内积结果才有可比性，比如：

????????第一组输入（1，2，3 ）归一化后（1/6 ，1/3 , 1/2 ）

????????第二组输入（100 ，200 ，300）归一化之后（1/6 ，1/3 , 1/2 ）

????????如果不做归一化，第二组结果的内积远大于第一组，但其实第一组的x 和第二组的向量x ????????只是大小不同，很相似

第二步，将内积的结果转换成概率，即使进行了归一化，内积的结果仍然是个数值，不是概率，这时就需要一个转换函数：sigmiod 函数。将内积的结果作为输入，得到0-1 之间的输出。

我们做了什么？

通过将感知机的输出，输入到Sigmoid 函数，我们得到了输入 x 向量和权重向量 w 的相似程度，若相似程度极高，那是不是说明了权重向量，学习到了输入向量 x 得特征呢？或者说，我们得到了一个用于区分向量x 和 w 的分类器，如果输出概率大于 0.5 , 可以大概将 x ,w 分为一类，如果概率为95% ，基本可以确认 x , w 为一类。

苹果香蕉分类器

感知机的输出到? 函数最终得到了一个分类器，但是不符合我们需求，我们要的分类应该是类似这样：输入颜色，形状，输出是香蕉苹果得概率，而不是输入颜色，形状和一个不明所以的权重 w 的相似程度， w应该是用来 ‘ 学习 ’ 香蕉苹果的颜色和外形特征的

二分类来识别苹果和香蕉：

我们可以得到以下概率：

????????P香蕉 = Sigmod (X_color * w11 + X_shape * w21)

????????P苹果 = Sigmod (X_color * w12 + X_shape * w22 )

我们如何根据输入的颜色和形状来得到是香蕉还是苹果的概率？假设苹果和香蕉的输入如下表： ?

刚开始，所有的权重 w 是随机的，没有记录任何香蕉苹果的特征，所有它不能分类

让我们来训练它：

????????使用苹果正确的参数来训练模型（1 ，1 ，苹果99% ，香蕉1%）：

????????????????P 苹果 = Sigmod (1* w12 + 1* w22 ) >=0.99

????????????????P 香蕉 = sigmod ( 1 *w11 + 1 * w21 ) < 0.01

????????使用香蕉正确的参数来训练模型（-1 ，2 ，苹果5% ，香蕉95%）：

????????????????P 香蕉 = sigmod ( -1 *w11 + 2 * w21 ) >= 0.95

????????????????P 苹果 = Sigmod (-1* w12 + 2* w22 ) <0.05

????????根据4个不等式得到：

????????????????Sigmod (w12 + w22 ) > > Sigmod ( 2* w22 - w12 )

????????????????sigmod ( 2 * w21 - w11 ) >> sigmod ( w11 + w21 )

不等式是 w21 和 w11 的关系，和 w12 和 w22 之间的关系

?sigmod函数已知，我们通过一定手段，就能得到 w11 和w21 的关系， w12 和 w22 的关系，它们分别记录了香蕉和苹果的颜色和外形特征。或许，用’学习‘了更合适。

推理：

香蕉和苹果的权重向量极其不相似，所以 W 记录了苹果和香蕉的颜色和形状特征。如果拿一个颜色 0.8 ( 不是那么红) ，形状（0.9）不是那么圆的水果，很大概率将识别为苹果，而不是香蕉，可以看到模型已经具备了对未知（以前没见过）颜色和形状的水果辨识能力。

神经网络

在苹果香蕉分类器中，我们使用了两个感知机搭建了系统模型，如果我们有要识别物体的更多特征呢，比如果肉的颜色，味道，是否有外皮。这些特征对应了更多的输入。

?在做复杂分类时，我们最常见的分类方法是逐级分类，上图中的隐藏层类似于下图中的上一级大类：

?有感知机构成的网络机构称为人工神经网络，与生物神经元的对比

神经网络的模型训练：

模型开始没有任何功能，权重随机
将训练数据输入到模型，经过模型的推理，得到一个推理结果
将推理结果与真实结果对比，求出误差。
通过误差，使用类似最小二乘法的方法，逐级去求使误差最小的权重（误差反向传播，梯度下降）
通过整个训练集的训练，模型的权重成功记录了识别体的特征
使用测试数据集来检验模型的准确度

误差反向传播一种通俗理解：

在输出层，我们有来自训练集的目标值，所以很容易得到误差，然后根据误差函数，可以求出使误差最小的输出层权重，但是隐藏层的误差我们没有定义，因为没有目标值。

由不同权重产生的不同比例的误差分配：可以认为因为输出结果 3/4 受节点1 影响， 1/4 受节点2 输出影响，所以总的输出误差更可能按权重的比例来分配。

?通过这样的误差分配规则，将误差进行反向传播，然后使用最小乘法来更新每一层的权重

?实际的误差反向传播：神经单元误差和偏导参考：《深度学习的数学》

神经网络的推理：

模型训练完成后，就具备了识别能力
输入要识别的物体输入，得到每个类别的概率，最大概率的表示最可能是什么

应用示例：数字识别 ?

? 输入层是像素点，这里是二值图片，像素点取值只能0和1，识别 0和1 ，输出层是 0，和 1 的概率，中间增加一层隐藏层，至于隐藏层的层数和节点个数，需要按实际情况测试。我们同样可以通过向量的相似性来理解这里的权重。

卷积神经网络(深度学习)

神经网络存在的问题

? ? ? ?

参数爆炸式增长
隐藏层层数和节点个数随缘，过多导致过拟合，过少模型表示能力不佳。不同的组合效果不同，没有科学的解释，这也是神经网络刚出现被人诟病的一点
深层的神经网络会出现梯度消失的情况：误差反向传播过程中，由输出成传到输入，每层分到误差的比例逐渐减小，导致靠近输入层的隐藏层参数无意义（误差小，几乎不会被自动调整）

卷积是什么

一个很形象的例子：一巴掌抽在脸上，脸肿了，随着时间推移，脸会慢慢消肿，假设脸肿的程度可以叠加，那么在 0-t 的时间内，不停的抽，在t 时刻，脸肿的程度就是 0-t 时间的卷积。用图像表示就是：

卷积在滤波中的使用：

????????离散：滑动加权滤波 ?

????????连续：高斯滤波

卷积神经网络的结构

卷积层：

卷积核：在二维图像处理中，如下图，选定的3x3 大小的过滤器S , 看作二维向量 W ，输入图片为二维向量 X , 根据感知机中提到的向量内积表示相似性，让向量 W 依次划过整张图片，与选中的区域做内积运算，再经过 Sigmoid 函数，得到图像中得部分区域与过滤器S 得相似程度。卷积层最终反应得是原始图片中，与过滤器S 相似的概率。也就是说过滤器提取了原始图片得特征分布。这个过滤器S 就称为卷积核，卷积核通常为5X5 大小，常用得卷积核见图像处理常用卷积核的效果。下图中得到的卷积层，明显在中间部分的概率比较大，因为卷积核更像 ‘2’ 的中间部位， ’2‘的头部也会有不错的概率，因为它部分相似。

池化层：

池化层用于信息压缩 , 有最大池化，平均值池化等

? ? ? ??

全连接输出：

类似神经网络

卷积神经网络的特点：

参数较神经网络大大减小，线性增加，卷积核的个数 * 5 + 输出全连接参数个数，卷积核的个数表示提取多少种特征
可以在池化层后再继续加卷积层，形成深层网络，同时增加卷积核的个数。
对于图像，使用传统的神经网络丢失了像素点的临近信息，而卷积神经网络完整保留，因此往往能得到更加优越的性能。

深度学习的应用场景

机器视觉（cv）

自然语言处理

部分地方超越，部分地方远远不如

3岁的小孩让他看一次大象真实图像，下次任何形式的大象都认得，比如涂鸦，不同品种，抽象，动画，或者反过来

Imagenet 数据集有1400多万幅图片，涵盖2万多个类别；其中有超过百万的图片有明确的类别标注和图像中物体位置的标注，具体信息如下：

自动驾驶

地图构建

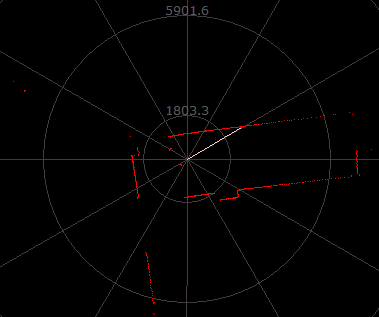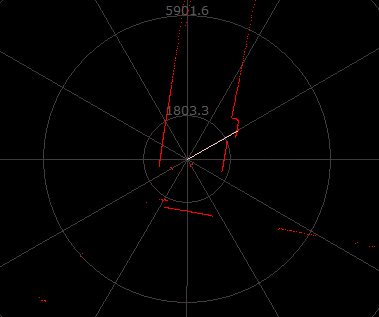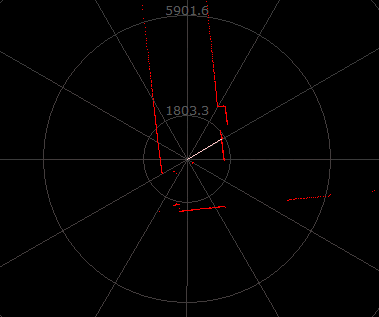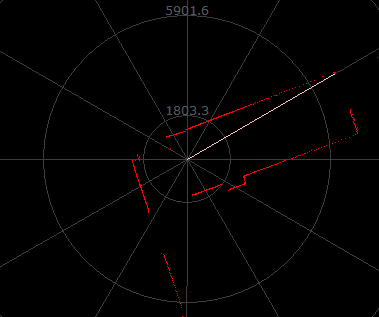
2D 平面地图：激光雷达(2D)

3D 点云地图：深度相机

实现：坐标变化

激光雷达或者深度相机或的数据是相对距离和角度，经过计算，可转换为相对坐标
开始建图时，选定一个绝对坐标零点，车体运动，根据IMU（惯性导航系统）和编码器以及雷达数据做融合，准确的得到机体的实时的绝对坐标
根据绝对坐标以及障碍物相对于车体的相对坐标，就能得到障碍物的绝对坐标，将障碍物一系列的点云坐标(线面有无数个点，只能抽取到特征点)保存就得到了地图。
导航：车体与障碍物都是绝对坐标，因此车体知道障碍物的存在，同时相对坐标和 IMU 编码器的数据会修正车体的绝对位置偏差

ROS 中的 TF 坐标变换

精确定位

室外定位：

GPS + IMU + 里程计(编码器)

室内定位：

（激光雷达）精确地图 + IMU + 里程计(编码器)

数据融合算法：

卡尔曼滤波（EKF UKF）
粒子滤波

教程 https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python

Kalman Filter Tutorial

基本原理： GPS 或者激光雷达产生的精确地图提供 绝对位置 ，由IMU 和里程计计算而得的 预测位置做数据融合，得到一个更精确的定位。

如上图假设GPS 的定位精度为 10m ，上图的B 。IMU 和编码器因为更精确，因此定位精度为 3m ，某次测量到上图的数据， GPS数据为170m ,

IMU和编码器的数据计算出来距离在 160m , 最终的比较准确的距离在哪呢？很显然是重合的地方。

如果比较巧合，两个不怎么可靠的传感器可能得到非常精确的结果。

路径规划

解决了地图和定位问题，我们已经知道了自己的位置和环境信息，接下来就是由出发地怎么去目的地了。由很多成熟的路径规划算法，这里以A* 算法为例。路径规划算法可以参考：https://github.com/AtsushiSakai/PythonRobotics

先来看看效果：

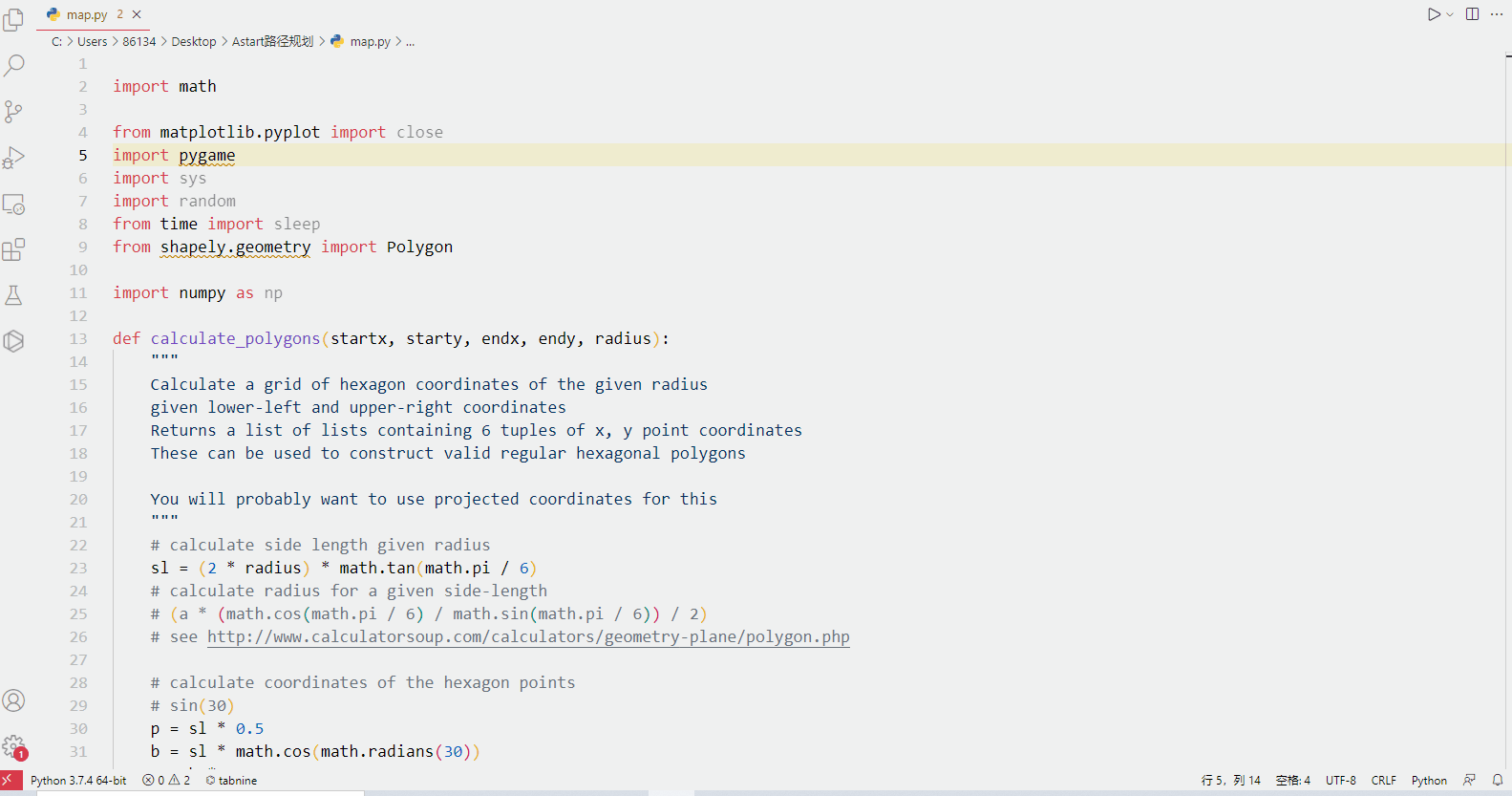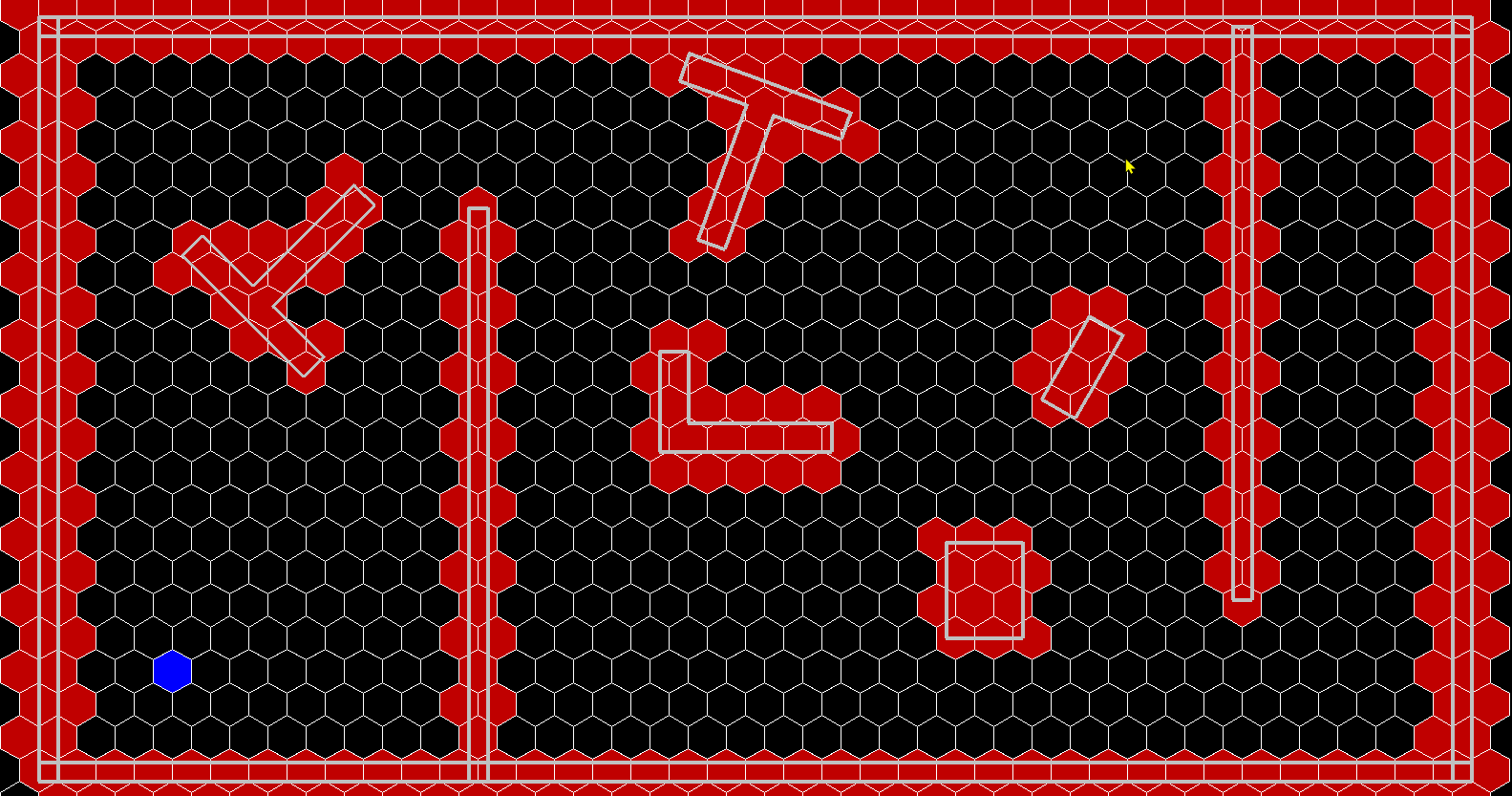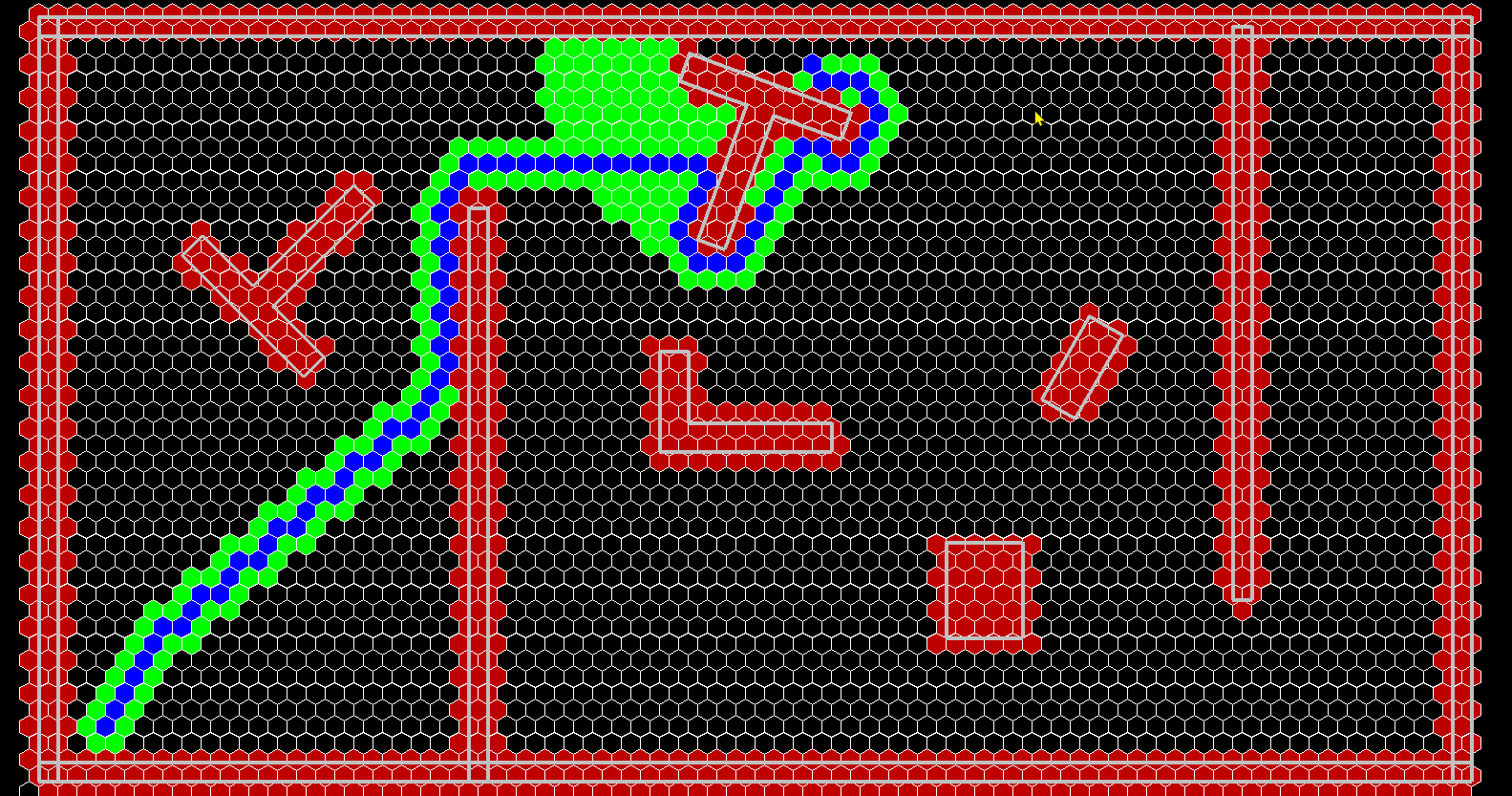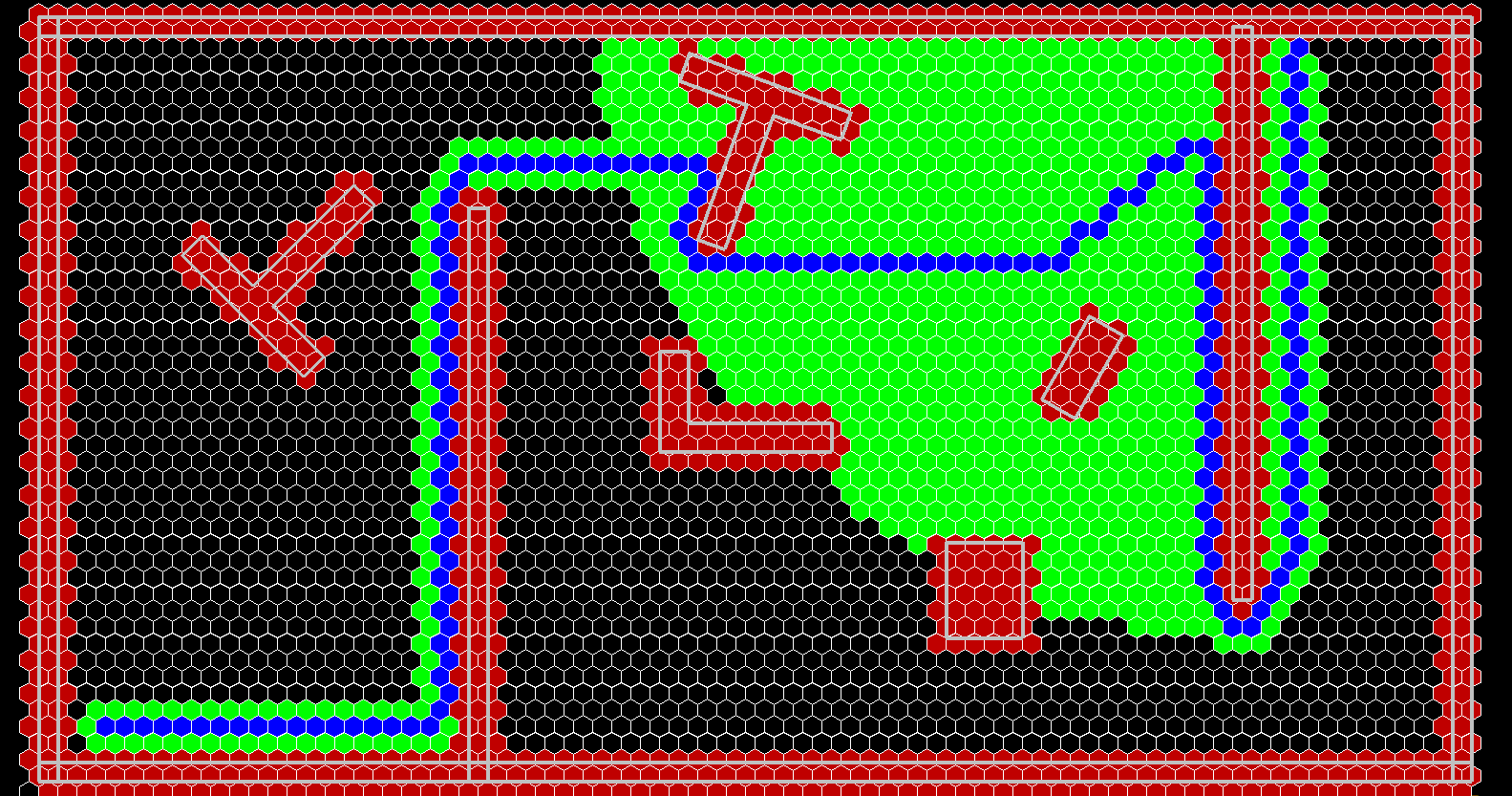
原理：

地图分割
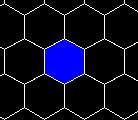
- 根据机器人的有效转弯半径来选择最小区域，这里以六边形作为最小区域，定义为节点
- 已知障碍物的绝对坐标，计算出地图中与障碍物有重合的节点，标记为不可通过的节点

确定起点和终点的区域，属于哪个节点
取起点临近的节点，依次计算代价，代价的计算考虑离起点的距离，以及离终点的距离，以及到邻近点的代价
- 单元移动代价：比如一开始方向向右，那么去往右边的节点代价最小，右上和右下其次，左边的代价依次增高
- 然后考虑当前节点距离终点的代价：距离
- 由起点到当前位置花费的总代价 + 终点距离的代价最小，即可选择下一个节点

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?