解决的第一个问题：在pycharm上导入了源代码斌且在上面安装Streamlit，pycharm中导入Streamlit，运行Streamlit_mu_tou_ren_的博客-CSDN博客
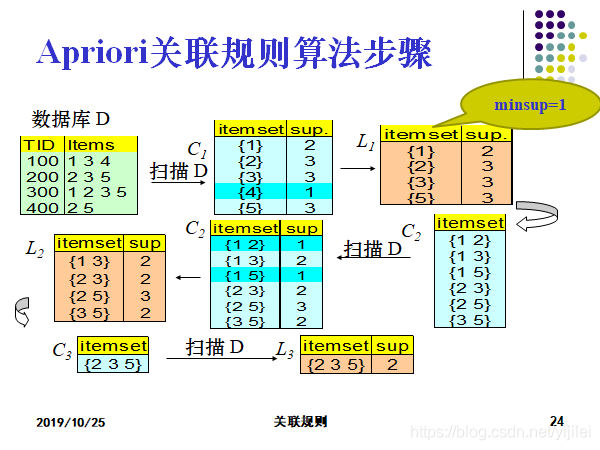关于Apriori关联规则的算法步骤；
具体挖掘的方法以及伪代码：
挖掘频繁项集?
连接步：为找Lk，通过Lk-1与自己连接产生候选k-项集的集合。该候选项集的集合记作Ck。
剪枝步：扫描数据库，确定Ck中每个候选的计数，从而确定Lk。然而，Ck可能很大，这样所涉及的计算量就很大。为压缩Ck，可以用以下办法使用Apriori性质：任何非频繁的(k-1)-项集都不是可能是频繁k-项集的子集。因此，如果一个候选k-项集的(k-1)-子集不在Lk-1中，则该候选也不可能是频繁的，从而可以由Ck中删除。
思路/伪代码如下：
思路/伪代码如下：??
输入：事务数据库D；最小Minsupport。
输出：D中的频繁项集L。
方法：? L1 = find_freL1(D); //找出频繁1-项集的集合L1
? ? ? ? ? ? ?for(k = 2; Lk-1 ≠ ?; k++) { //产生候选，并剪枝
? ? ? ? ? ? ? ? ? ? Ck = aproiri_gen(Lk-1,min_sup);
? ? ? ? ? ? ? ? ? ??for each transaction t∈D{ //扫描D进行候选计数
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? Ct = subset(Ck,t); //得到t的子集
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?for each candidate c∈Ct
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?c.count++; //支持度计数
? ? ? ? ? ? ? ? ? ? ? }
? ? ? ? ? ? ? ? ? ? ?Lk={c∈Ck| c.count ≥min_sup} //返回候选项集中不小于最小支持度的项集
? ? ? ? ? ? ?}
? ? ? ? ? ? ?return L = ∪kLk；//所有的频繁集
第一步（自身进行连接 join）
Procedure apriori_gen(Lk-1: frequent (k-1)-itemset; min_sup)
1) for each itemset l1∈Lk-1
2) for each itemset l2∈Lk-1
3) if(l1[1]=l2[1])∧...∧(l1[k-2]=l2[k-2])∧(l1[k-1]<l2[k-1]) then
{
????????????????c = l1 l2; //连接步：l1连接l2 //连接步产生候选
?????????????????if??has_infrequent_subset(c,Lk-1)??then?delete c; //剪枝步：删除非频繁候选
? ? ????????????????else add c to Ck;
?}
?return Ck;
第二步：剪枝（prune）
Procedure has_infrequent_subset(c:candidate k-itemset; Lk-1:frequent (k-1)-itemset)
//使用先验定理
1) for each (k-1)-subset s of c
2) if c?Lk-1 then
3) return TRUE;
4) return FALSE;??
第二个问题：
如何在UCI上选择适合Apriori算法的数据集以及实现相关数据集的导入和使用？
生成关联规则
?
书上的原例：
# @ClassName:灿灿
# @Description:Apriori主算法-简单
# @Data: 11:07
# @title:
# @Author:灿灿睡醒了
#样本事务数据库(书上的样例)
def loadDataSet() :
return [['A','B','C', 'D'],
['B', 'C', 'E'],
['A', 'B', 'C', 'E'],
['B','D', 'E'],
['A','B','C','D']]
def createC1(dataSet) :
"""构建C1
功能：将所有元素转换为frozenset型字典，存放到列表中
:param dataSet: 原始数据集合
:return: 最初的候选频繁项
transaction:代表每一项事务
"""
C1 = []
for transaction in dataSet :
for item in transaction :
if not [item] in C1 :
C1.append([item])
C1.sort()
# 使用frozenset是为了后面可以将这些值作为字典的键
return list(map(frozenset, C1)) # frozenset一种不可变的集合，set可变集合
def scanD(D, Ck, minSupport) :
"""
函数功能：过滤掉不符合支持度的集合
具体逻辑：
遍历原始数据集和候选频繁项集，统计频繁项集出现的次数，
由此计算出支持度，在比对支持度是否满足要求，
不满足则剔除，同时保留每个数据的支持度。
:param D: 原始数据转化后的字典
:param Ck: 候选频繁项集
:param minSupport: 最小支持度
:return: 频繁项集列表retList 所有元素的支持度字典
"""
ssCnt = {}
for tid in D :
for can in Ck :
if can.issubset(tid) : # 判断can是否是tid的《子集》 （这里使用子集的方式来判断两者的关系）
if can not in ssCnt : # 统计该值在整个记录中满足子集的次数（以字典的形式记录，frozenset为键）
ssCnt[can] = 1
else :
ssCnt[can] += 1
numItems = float(len(D))#字典的长度；
retList = [] # 重新记录满足条件的数据值（即支持度大于阈值的数据）
supportData = {} # 每个数据值的支持度
for key in ssCnt :
support = ssCnt[key] / numItems
if support >= minSupport :
retList.insert(0, key)
supportData[key] = support
return retList, supportData # 排除不符合支持度元素后的元素 每个元素支持度
def aprioriGen(Lk, k) :
"""
功能： 生成所有可以组合的集合
具体逻辑：通过每次比对频繁项集相邻的k-2个元素是否相等，如果相等就构造出一个新的集合
:param Lk: 频繁项集列表Lk
:param k: 项集元素个数k，当前组成项集的个数
:return: 频繁项集列表Ck
举例：[frozenset({2, 3}), frozenset({3, 5})] -> [frozenset({2, 3, 5})]
"""
retList = []
lenLk = len(Lk)#记录有多少个频繁项集；
for i in range(lenLk) : # 两层循环比较Lk中的每个元素与其它元素
for j in range(i + 1, lenLk) :
L1 = list(Lk[i])[:k - 2] # 将集合转为list后取值
L2 = list(Lk[j])[:k - 2]
L1.sort();
L2.sort() # 这里说明一下：该函数每次比较两个list的前k-2个元素，如果相同则求并集得到k个元素的集合
if L1 == L2 :
retList.append(Lk[i] | Lk[j]) # 求并集
return retList # 返回频繁项集列表Ck
def apriori(dataSet, minSupport=0.4) :
"""
function：apriori算法实现
:param dataSet: 原始数据集合
:param minSupport: 最小支持度
:return: 所有满足大于阈值的组合 集合支持度列表
"""
D = list(map(set, dataSet)) # 转换列表记录为字典，为了方便统计数据项出现的次数
C1 = createC1(dataSet) # 将每个元素转会为frozenset字典 [frozenset({A}), frozenset({B}), frozenset({C}), frozenset({D}), frozenset({E})]
# 初始候选频繁项集合
L1, supportData = scanD(D, C1, minSupport) # 过滤数据,去除不满足最小支持度的项
# L1 频繁项集列表 supportData 每个项集对应的支持度
L = [L1]
k = 2
while (len(L[k - 2]) > 0) : # 若仍有满足支持度的集合则继续做关联分析
Ck = aprioriGen(L[k - 2], k) # Ck候选频繁项集
Lk, supK = scanD(D, Ck, minSupport) # Lk频繁项集
supportData.update(supK) # 更新字典（把新出现的集合:支持度加入到supportData中）
L.append(Lk)
k += 1 # 每次新组合的元素都只增加了一个，所以k也+1（k表示元素个数）
return L, supportData
def calcConf(freqSet, H, supportData, brl, minConf=0.6) :
"""
对规则进行评估 获得满足最小可信度的关联规则
:param freqSet: 集合元素大于两个的频繁项集
:param H:频繁项单个元素的集合列表
:param supportData:频繁项对应的支持度
:param brl:关联规则
:param minConf:最小可信度
"""
prunedH = [] # 创建一个新的列表去返回
for conseq in H :
conf = supportData[freqSet] / supportData[freqSet - conseq] # 计算置信度
if conf >= minConf :
print(freqSet - conseq,'-->',conseq,'conf:',conf)
brl.append((freqSet - conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.6) :
"""
功能：生成候选规则集合
:param freqSet: 集合元素大于两个的频繁项集
:param H:频繁项单个元素的集合列表
:param supportData:频繁项对应的支持度
:param brl:关联规则
:param minConf:最小可信度
:return:
"""
m = len(H[0])
if (len(freqSet) > (m + 1)) : # 尝试进一步合并
Hmp1 = aprioriGen(H, m + 1) # 将单个集合元素两两合并
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
if (len(Hmp1) > 1) : # need at least two sets to merge
rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
def generateRules(L, supportData, minConf=0.6) : # supportData 是一个字典
"""
功能：获取关联规则的封装函数
:param L:频繁项列表
:param supportData:每个频繁项对应的支持度
:param minConf:最小置信度
:return:强关联规则
"""
bigRuleList = []
for i in range(1, len(L)) : # 从为2个元素的集合开始
for freqSet in L[i] :
# 只包含单个元素的集合列表
H1 = [frozenset([item]) for item in freqSet] # frozenset({2, 3}) 转换为 [frozenset({2}), frozenset({3})]
# 如果集合元素大于2个，则需要处理才能获得规则
if (i > 1) :
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf) # 集合元素 集合拆分后的列表 。。。
else :
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
if __name__ == "__main__":
# 初始化数据
dataSet = loadDataSet()
# 计算出频繁项集合对应的支持度
L, suppData = apriori(dataSet,minSupport=0.4)
print("频繁项集：")
for i in L:
for j in i:
print(list(j))
# 得出强关联规则
print("关联规则：")
rules = generateRules(L, suppData, minConf=0.6)
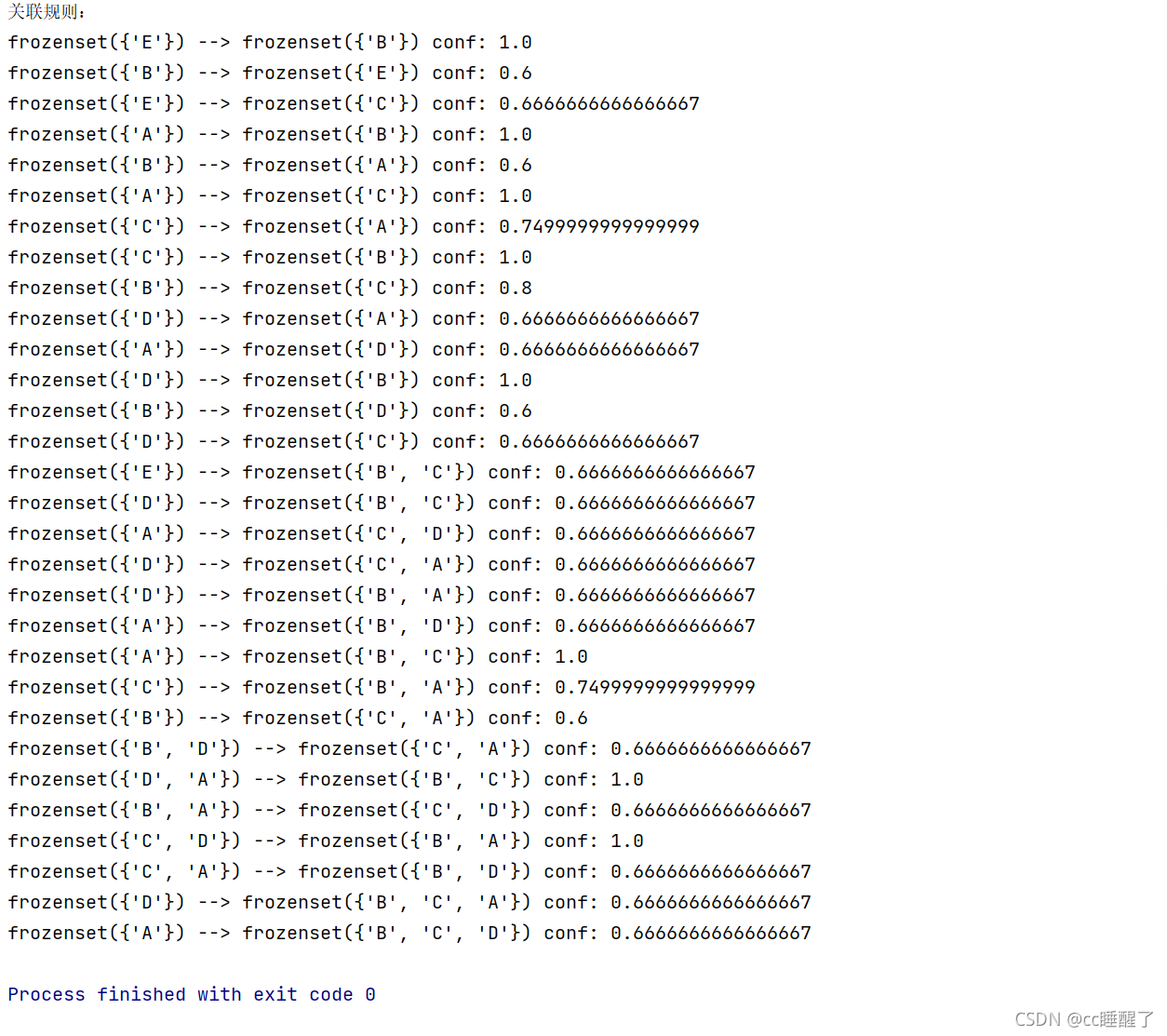
算法的结果:
关联规则：
ID3?
?
# @ClassName:灿灿
# @Description:宁愿累死自己，也要卷死同学
# @Data: 10:54
# @title:
# @Author:灿灿睡醒了
# -*- coding: UTF-8 -*-
from math import log
import operator
"""
函数说明:创建测试数据集
"""
def createDataSet():
dataSet = [[1, 1, 0, '有电脑'], # 数据集
[0, 0, 0, '有电脑'],
[1, 1, 0, '有电脑'],
[1, 1, 0, '有电脑'],
[1, 0, 0, '没有电脑'],
[1, 0, 1, '没有电脑']]
labels = ['性别', '学生', '民族'] # 分类属性
return dataSet, labels # 返回数据集和分类属性
"""
函数说明:计算给定数据集的经验熵(香农熵)
Parameters:
dataSet - 数据集
Returns:
shannonEnt - 经验熵(香农熵)
"""
def calcShannonEnt(dataSet):
numEntires = len(dataSet) # 返回数据集的行数
labelCounts = {} # 保存每个标签(Label)出现次数的字典
for featVec in dataSet: # 对每组特征向量进行统计
currentLabel = featVec[-1] # 提取标签(Label)信息
if currentLabel not in labelCounts.keys(): # 如果标签(Label)没有放入统计次数的字典,添加进去
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # Label计数
shannonEnt = 0.0 # 经验熵(香农熵)
for key in labelCounts: # 计算香农熵
prob = float(labelCounts[key]) / numEntires # 选择该标签(Label)的概率
shannonEnt -= prob * log(prob, 2) # 利用公式计算
return shannonEnt # 返回经验熵(香农熵)
"""
函数说明:按照给定特征划分数据集
Parameters:
dataSet - 待划分的数据集
axis - 划分数据集的特征
value - 需要返回的特征的值
"""
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 创建返回的数据集列表
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value:
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:]) # 将符合条件的添加到返回的数据集
retDataSet.append(reducedFeatVec)
return retDataSet # 返回划分后的数据集
"""
函数说明:选择最优特征
Parameters:
dataSet - 数据集
Returns:
bestFeature - 信息增益最大的(最优)特征的索引值
"""
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 计算数据集的香农熵
bestInfoGain = 0.0 # 信息增益
bestFeature = -1 # 最优特征的索引值
for i in range(numFeatures): # 遍历所有特征
# 获取dataSet的第i个所有特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 创建set集合{},元素不可重复
newEntropy = 0.0 # 经验条件熵
for value in uniqueVals: # 计算信息增益
subDataSet = splitDataSet(dataSet, i, value) # subDataSet划分后的子集
prob = len(subDataSet) / float(len(dataSet)) # 计算子集的概率
newEntropy += prob * calcShannonEnt(subDataSet) # 根据公式计算经验条件熵
infoGain = baseEntropy - newEntropy # 信息增益
print("第%d个特征的增益为%.3f" % (i, infoGain)) # 打印每个特征的信息增益
if (infoGain > bestInfoGain): # 计算信息增益
bestInfoGain = infoGain # 更新信息增益，找到最大的信息增益
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
"""
函数说明:统计classList中出现此处最多的元素(类标签)
Parameters:
classList - 类标签列表
Returns:
sortedClassCount[0][0] - 出现此处最多的元素(类标签)
"""
def majorityCnt(classList):
classCount = {}
for vote in classList: # 统计classList中每个元素出现的次数
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) # 根据字典的值降序排序
return sortedClassCount[0][0] # 返回classList中出现次数最多的元素
"""
函数说明:递归构建决策树
Parameters:
dataSet - 训练数据集
labels - 分类属性标签
featLabels - 存储选择的最优特征标签
Returns:
myTree - 决策树
"""
def createTree(dataSet, labels, featLabels):
classList = [example[-1] for example in dataSet] # 取分类标签（是否有电脑—）
if classList.count(classList[0]) == len(classList): # 如果类别完全相同则停止继续划分
return classList[0]
if len(dataSet[0]) == 1: # 遍历完所有特征时返回出现次数最多的类标签
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) # 选择最优特征
bestFeatLabel = labels[bestFeat] # 最优特征的标签
featLabels.append(bestFeatLabel)
myTree = {bestFeatLabel: {}} # 根据最优特征的标签生成树
del (labels[bestFeat]) # 删除已经使用特征标签
featValues = [example[bestFeat] for example in dataSet] # 得到训练集中所有最优特征的属性值
uniqueVals = set(featValues) # 去掉重复的属性值
for value in uniqueVals:
subLabels = labels[:]
# 递归调用函数createTree(),遍历特征，创建决策树。
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels)
return myTree
"""
函数说明:使用决策树执行分类
Parameters:
inputTree - 已经生成的决策树
featLabels - 存储选择的最优特征标签
testVec - 测试数据列表，顺序对应最优特征标签
Returns:
classLabel - 分类结果
"""
def classify(inputTree, featLabels, testVec):
firstStr = next(iter(inputTree)) # 获取决策树结点
secondDict = inputTree[firstStr] # 下一个字典
featIndex = featLabels.index(firstStr)
for key in secondDict.keys():
if testVec[featIndex] == key:
if type(secondDict[key]).__name__ == 'dict':
classLabel = classify(secondDict[key], featLabels, testVec)
else:
classLabel = secondDict[key]
return classLabel
if __name__ == '__main__':
dataSet, labels = createDataSet()
featLabels = []
myTree = createTree(dataSet, labels, featLabels)
print(myTree)
testVec = [1,0,0] # 测试数据
result = classify(myTree, featLabels, testVec)
print(result)问题：最后分类的结果不正确？
K-means算法：
数据集：
?
# @ClassName:灿灿
# @Data: 20:11
# @title:
# @Author:灿灿睡醒了
import random
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 计算欧式距离
def calcDis(dataSet, centroids, k):
clalist = []
for data in dataSet:
diff = np.tile(data, (k, 1)) - centroids
# 相减 (np.tile(a,(2,1))就是把a先沿x轴复制1倍，即没有复制，仍然是 [0,1,2]。 再把结果沿y方向复制2倍得到array([[0,1,2],[0,1,2]]))
squaredDiff = diff ** 2 # 平方
squaredDist = np.sum(squaredDiff, axis=1) # 和 (axis=1表示行)
distance = squaredDist ** 0.5 # 开根号
clalist.append(distance)
clalist = np.array(clalist) # 返回一个每个点到质点的距离len(dateSet)*k的数组
return clalist
# 计算质心
def classify(dataSet, centroids, k):
# 计算样本到质心的距离
clalist = calcDis(dataSet, centroids, k)
# 分组并计算新的质心
minDistIndices = np.argmin(clalist, axis=1) # axis=1 表示求出每行的最小值的下标
newCentroids = pd.DataFrame(dataSet).groupby(minDistIndices).mean()
# DataFramte(dataSet)对DataSet分组，groupby(min)按照min进行统计分类，mean()对分类结果求均值
newCentroids = newCentroids.values
# 计算变化量
changed = newCentroids - centroids
return changed, newCentroids
# 使用k-means分类
def kmeans(dataSet, k):
# 随机取质心
centroids = random.sample(dataSet, k)
# 更新质心 直到变化量全为0
changed, newCentroids = classify(dataSet, centroids, k)
while np.any(changed != 0):
changed, newCentroids = classify(dataSet, newCentroids, k)
centroids = sorted(newCentroids.tolist()) # tolist()将矩阵转换成列表 sorted()排序
# 根据质心计算每个集群
cluster = []
clalist = calcDis(dataSet, centroids, k) # 调用欧拉距离
minDistIndices = np.argmin(clalist, axis=1)
for i in range(k):
cluster.append([])
for i, j in enumerate(minDistIndices): # enymerate()可同时遍历索引和遍历元素
cluster[j].append(dataSet[i])
return centroids, cluster
# 创建数据集
def createDataSet():
return [[1, 1], [2, 1], [1, 2], [2, 2], [4, 3], [5, 3],[4,4],[5,4]]
if __name__ == '__main__':
dataset = createDataSet()
centroids, cluster = kmeans(dataset, 2)
print('质心为：%s' % centroids)
print('集群为：%s' % cluster)
for i in range(len(dataset)):
plt.scatter(dataset[i][0], dataset[i][1], marker='o', color='green', s=40, label='原始点')
# 记号形状 颜色 点的大小 设置标签
for j in range(len(centroids)):
plt.scatter(centroids[j][0], centroids[j][1], marker='x', color='red', s=50, label='质心')
plt.show
实验结果
?