[人工智能]深度学习算法笔记（1）--优化器相关

深度学习算法笔记（1）–优化器相关

个人笔记，记录思考过程，已注明参考文献。

一、优化器

1. 梯度下降相关

1.1 梯度下降法（Gradient Descent Algorithm，GD）

一层感知机的正向传递过程

$a_1^{[l?1]}$：表示第$[l?1]$层中第$1$个感知机的输出。那么第$[l?1]$层的总输出为$a^{[l?1]}$。
$W_{i,1}^{[l]}$：”表示第$[l]$层的第$i$个感知机上的对应上一层第$1$个输入的权重信息。而$b_i^{[l]}$表示偏置。
那么第$[l]$层将所有输入整合过后的结果为$z_i^{[l]}$,计算过程为：

最后通过激活函数（sigmoid）得到该感知机的输出
$$\sigma (z_i^{[l]})=a_i^{[l]}$$
多个感知机的正向传递过程

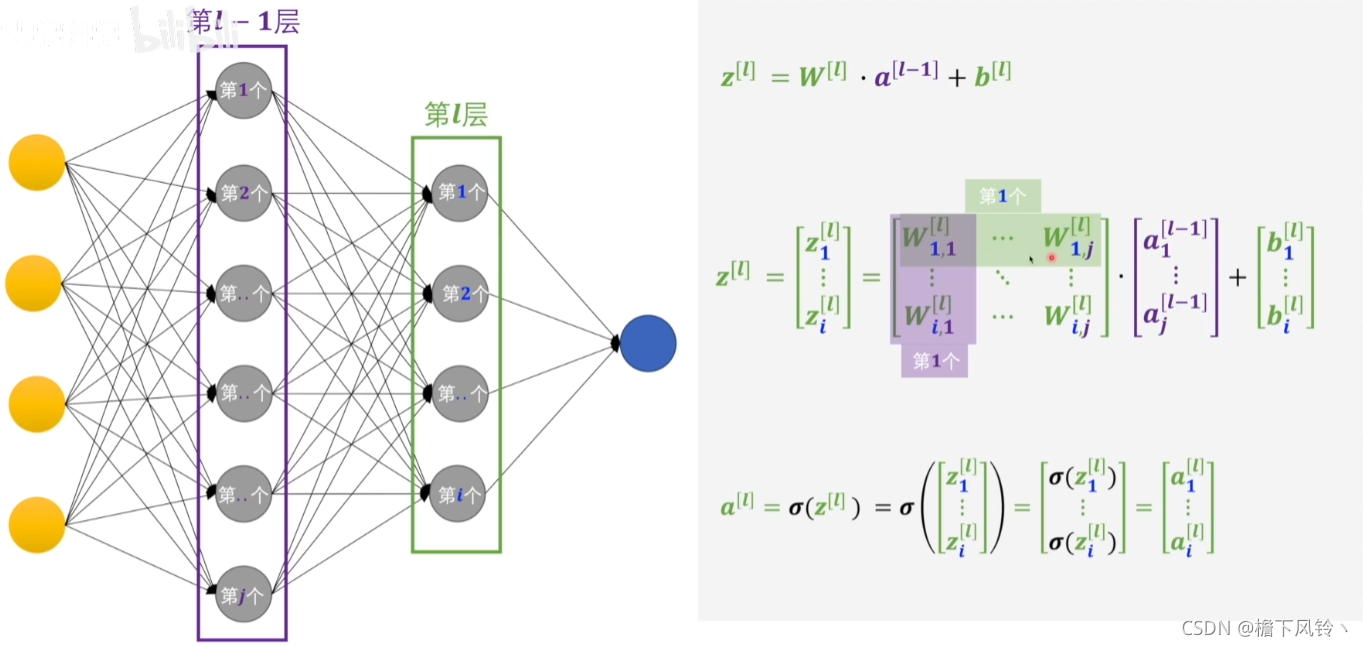
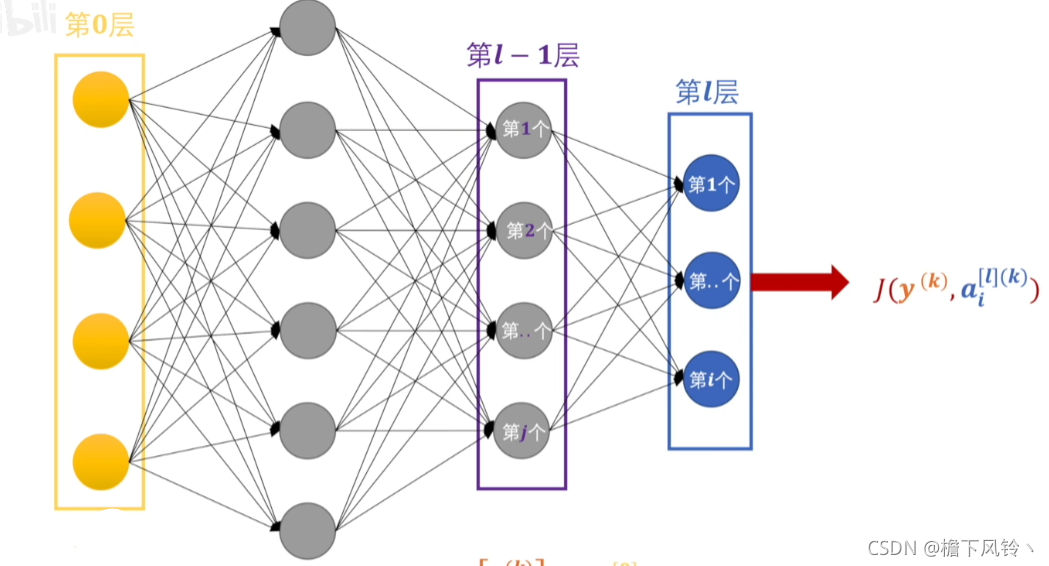
那么，隐藏层的输出结果可以假设为 $a^{[l]}$（二分类任务中）或者是$a_i^{[l]}$（多分类任务中）
引入损失函数

? 这里使用交叉熵损失函数（PS：详见第二章第一节交叉熵损失函数），简单定义为：
$$J(y^{(k)},a^{[l](k)})$$
其中，$y^{(k)}$表示标签，来源于人工标注，可以是分类任务的 $label$，亦或是分割任务中的 $mask$。
具体的，输入数据定义为：$x=(x^{(1)},x^{(2)},..,x^{(k)},...,x^{(m)}$,$m$表示一个batch的大小，$k$为一个$batch$中的第$k$个数据。
对于像素级的分割任务来说，每个像素点都是有具体划分的，因此，

$x_1^{(k)}$表述第$k$个数据中的第一个像素点的值。而$a_1^{(0)}$则为第0层中第1个像素点的输出。
那么综上，损失已经得到，下面开始反向传播。
反向传播

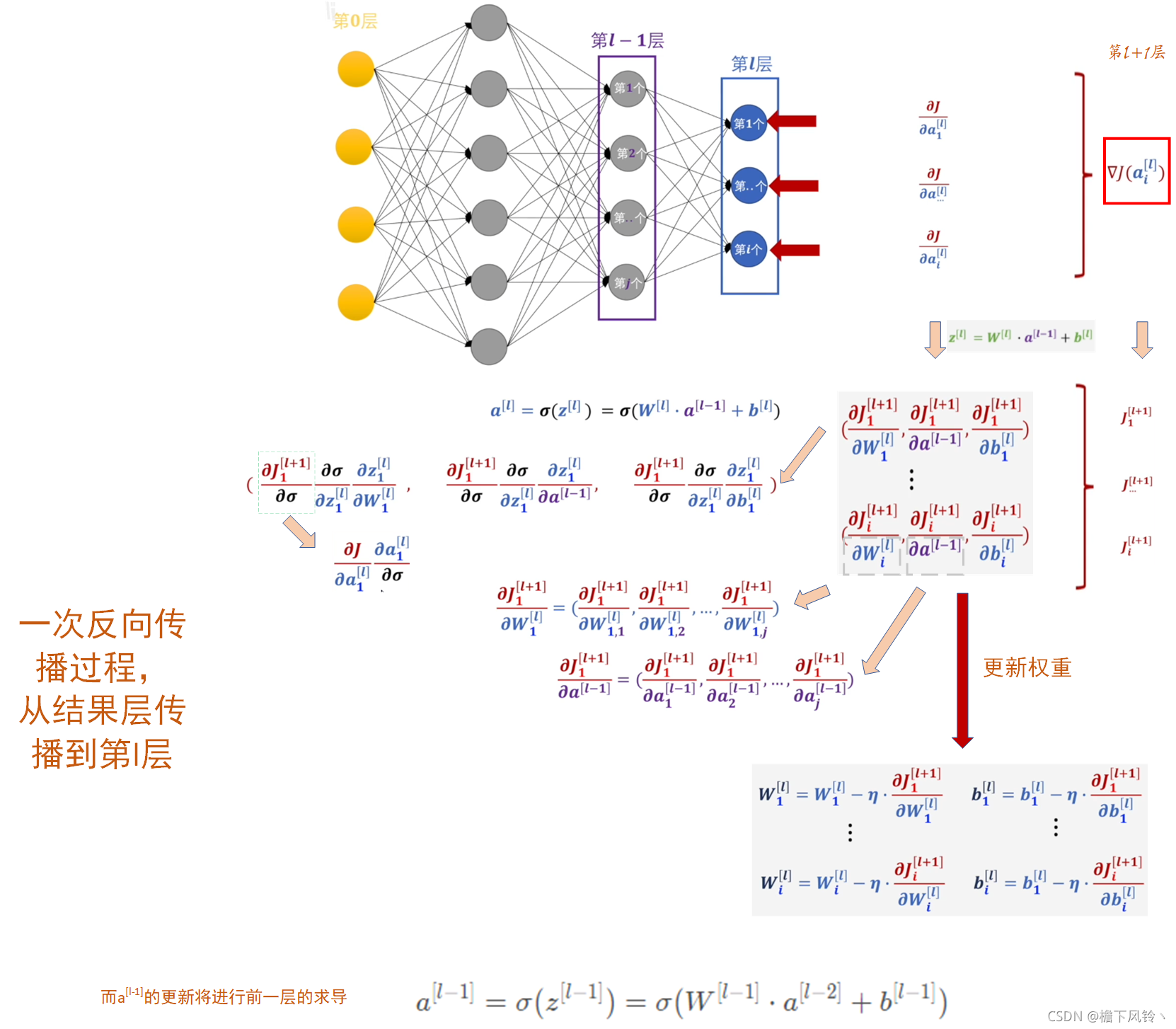
以上过程为反向传播的具体公式表示。$\eta$ 表示学习率 $lr$。
可以看到，梯度下降法是基于输入数据量大小进行计算的。

1.2 批量梯度下降法（Batch Gradient Descent, BGD）

批量梯度下降法是最原始的形式，相对于$1.1$中所描述的一样，这里是指所有的样本（整个数据集）。
优点：
?（1）一次迭代是对所有样本进行计算，此时利用矩阵进行运算，实现了并行。
?（2）由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，批量梯度下降一定能够得到全局最优解。
缺点：
?（1）有时我们会遇到样本数目 m 很大的训练集合，如果有几十上百万，甚至上亿的训练样本。这意味着我们每执行一次批梯度下降算法，都要对m个样本进行求和。我们的程序也就需要检测这上百万的样本，甚至我们完成值下降的第一步都十分困难。这样会导致，训练过程很慢，花费很长的时间。

1.3 随机梯度下降法（Stochastic Gradient Descent, SGD）

相比于批量梯度下降取全部样本的交叉熵之和后去平均的方法，随机梯度下降则将交叉熵平方后再除以2，意思是说每次迭代使用一个样本来对参数进行更新。这样能够使训练速度加快。（batch_size=1）
优点：
?（1）由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。
缺点：
?（1）准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
?（2）可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
?（3）不易于并行实现。

1.4 小批量梯度下降法（Mini-batch Gradient Descent, MBGD）

考虑到批梯度的方式在每次迭代时都要使用到所有的样本，这徒然增加了计算成本，因此，小批量梯度下降法（MBGD）利用了部分样本代替所有样本来参与计算的思想，引入了mini-batch的概念。
假定mini-batch为10个样本，总样本为100个，则每10个样本进行一次改变权值。可以认为mini-batch等于batch，所以，batch的大小直接影响了模型的训练速度与寻优能力。
batch的选择带来的影响：
?（1）在合理地范围内，增大batch的好处：
???a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
???b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
???c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
?（2）盲目增大batch的坏处：
???a. 内存利用率提高了，但是内存容量可能撑不住了。
???b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
???c. batch增大到一定程度，其确定的下降方向已经基本不再变化。
优点：
?（1）通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
?（2）每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
?（3）可实现并行化。
缺点：
?（1）batch_size的不当选择可能会带来一些问题。

2. 动量法相关

写在前面：$\theta$(参数)的移动基于动量$m_t$。

2.1 动量法（Momentum）

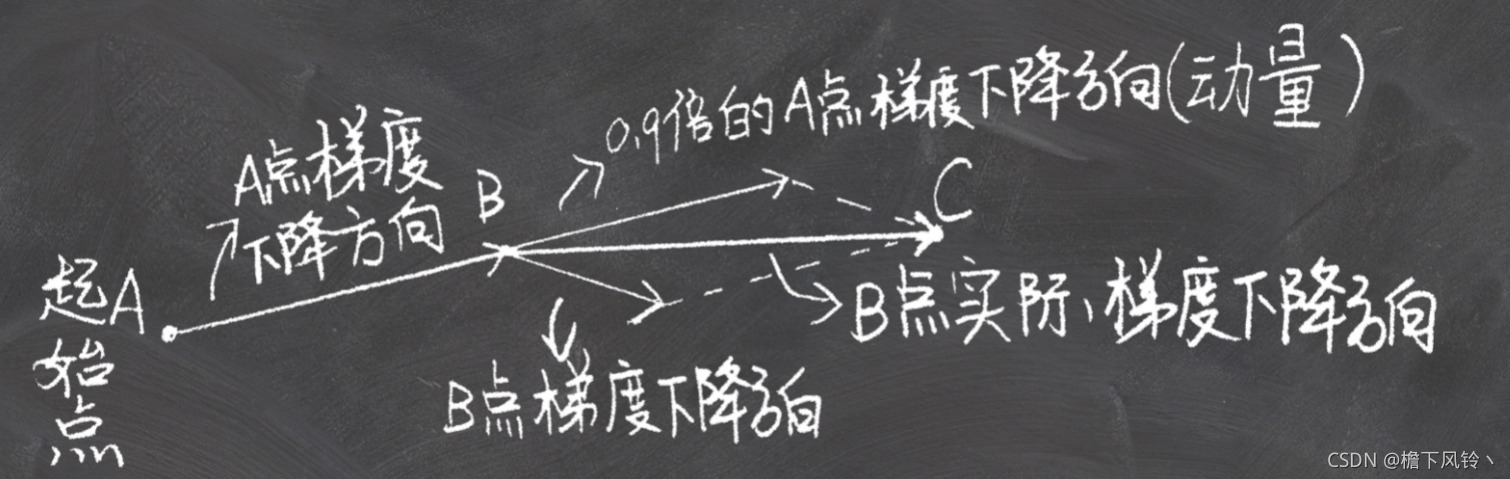
动量法在实际梯度优化时表现方式如上图所示。其具体公式如下：
$$\begin{gathered} g_t=?J({\theta }_{t?1}) \\ {m}_t={\beta }_1?m_{t?1}?lr?g_t \\ \theta ={\theta }_{t?1}+m_t \end{gathered}$$
其中，$m_t$是一阶动量，${\beta }_1$是动量因子，$t$表示迭代的次数，$lr$表示学习率，$J$为模型目标函数，${\theta }_t$表示当前迭代时需要更新的模型参数，$g_t$是目标函数的梯度。

2.2 Nesterov Momentum

$$\begin{gathered} m_t={\beta }_1?m_{t?1}?lr??J\left({\theta }_{t?1}+{\beta }_1?m_{t?1}\right) \\ {\theta }_t={\theta }_{t?1}+m_t \end{gathered}$$

5. Adagrad

针对于学习率，对学习率进行自适应约束，间接影响参数。
$$\begin{gathered} n_t=n_{t?1}+g_t^2 \\ \Delta {\theta }_t=?\frac{lr}{\sqrt{n_t+\epsilon }}?g_t \\ {\theta }_t={\theta }_{t?1}+\Delta {\theta }_t \end{gathered}$$
其中$\epsilon$很小，为了保证分母不为0；$n_t$是梯度平方的累积，为二阶动量，初始为0；
优点：不需要手工调节学习率，在稀疏数据场景下效果较好，对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。
缺点：随着时间的增长，单调增长，单调减少，有可能过早的变为0，训练过早的结束。而且依然依赖与人工设定的学习率。

6. RMSprop

由于AdaGrad单调递减的q学习率变化过于激进，RMSprop只关注过去一段时间的梯度平均值，离的时间越远越不重要。
$$\begin{gathered} n_t={\beta }_1{n}_{t?1}+\left(1?{\beta }_1\right)g_t^2 \\ \Delta {\theta }_t=?\frac{lr}{\sqrt{n_t+\epsilon }}?g_t \\ {\theta }_t={\theta }_{t?1}+\Delta {\theta }_t \end{gathered}$$
$n_t$是梯度平方的累积，为二阶动量，初始为0；${\beta }_1$为动量因子。

7. Adadelta

RMSprop依然需要自己设定全局学习率，因此Adadelta在RMSprop的基础上，用参数更新的平方来替代全局学习率的位置，这样就可以省略全局学习率了。
解决两个问题：
1.在整个训练过程中，学习率不断下降；
2.需要手动选择全局学习率。
$$\begin{gathered} n_t={\beta }_1{n}_{t?1}+\left(1?{\beta }_1\right)g_t^2 \\ {V}_t=\gamma V_{t?1}+(1?\gamma )△{\theta }_t^2 \\ \Delta {\theta }_t=?\frac{\sqrt{V_t+\epsilon }}{\sqrt{n_t+\epsilon }}?g_t \\ {\theta }_t={\theta }_{t?1}+\Delta {\theta }_t \end{gathered}$$

8. 自适应矩估计（Adaptive moment estimation，Adam）

融合一阶动量和二阶动量。
$$\begin{gathered} m_t={\beta }_1{m}_{t?1}+\left(1?{\beta }_1\right)g_t \\ {n}_t={\beta }_2{n}_{t?1}+\left(1?{\beta }_2\right)g_t^2 \end{gathered}$$
因为当$m_t$和$n_t$一开始被初始化为 0 时，最初的几步通常会偏向0，表示参数更新太慢。
他们使用偏差纠正系数，来修正一阶矩和二阶矩的偏差：
$$\begin{gathered} {\hat{m}}_t=\frac{m_t}{1?{\beta }_1^t} \\ \widehat{n_t}=\frac{n_t}{1?{\beta }_2^t} \\ \Delta {\theta }_t=?\eta ?\frac{{\hat{m}}_t}{\sqrt{{\hat{n}}_t+\epsilon }} \\ {\theta }_t={\theta }_{t?1}+\Delta {\theta }_t \end{gathered}$$

9.AdamW

$$\begin{gathered} {\hat{m}}_t=\frac{m_t}{1?{\beta }_1^t} \\ \widehat{n_t}=\frac{n_t}{1?{\beta }_2^t} \\ \Delta {\theta }_t=?\eta ?(\frac{{\hat{m}}_t}{\sqrt{{\hat{n}}_t+\epsilon }}+\lambda {\theta }_{t?1}) \\ {\theta }_t={\theta }_{t?1}+\Delta {\theta }_t \end{gathered}$$

二、损失函数

1.交叉熵损失函数

什么是交叉熵损失函数？

二分类

在二分的情况下，模型最后需要预测的结果只有两种情况，对于每个类别我们的预测得到的概率为p和 1-p ，此时表达式为：
$$L=\frac{1}{N}\sum _i{L}_i=\frac{1}{N}\sum _i?\left[y_i?\log \left(p_i\right)+\left(1?y_i\right)?\log \left(1?p_i\right)\right]$$
其中：
$$\begin{gathered} y_i?表示样本i的label，正类为1，负类为0 \\ {p}_i?表示样本i预测为正类的概率 \end{gathered}$$

三、功能函数

1.均值函数（mean function）—>可以用期望表示$E(X)$

1） 标题算术平均数（Arithmetic Mean）

优点：相比于中位数、众数，更少收到随机因素的影响
缺点：更容易收到极端值（biased value）的影响
2) 几何平均数（Geometric Mean）

优点:适用于对比率数据的平均，主要用于计算数据平均增长率
3) 调和平均数（Harmonic Mean）

优点：计算平均速率，感觉很多paper都在用，用于计算平均速率
4) 平方平均数（Quadratic Mean）

优点：是2次方的广义平均数的表达式。可以定义在连续区间。常用来计算一组数据与某个数据之间的平均差。

2.协方差函数（covariance function）

1）协方差
对于单一的随机变量，我们考虑其期望$E(X)$与方差$D(X)$。
当想比较两个随机变量，我们引入了协方差(两个随机变量可以对应数据分析中的两个字段，即可以不属于同一定义域)。协方差，看名字就知道，其定义来源于方差。对两个随机变量X和Y，其协方差就是：

2）协方差函数
设随机过程为$X(t)$，定义域为$D$，$t_1$,$t_2$$?$$D$，定义协方差函数$C_X(t_1,t_2)$为$t_1$与$t_2$的协方差，形成的函数。
C X ( t 1 , t 2 ) = E { [ X ( t 1 ) ? μ X ( t 1 ) ] [ X ( t 2 ) ? μ X ( t 2 ) ] } C_{X}\left(t_{1}, t_{2}\right)=E\left\{\left[X\left(t_{1}\right)-\mu_{X}\left(t_{1}\right)\right]\left[X\left(t_{2}\right)-\mu_{X}\left(t_{2}\right)\right]\right\} CX?(t1?,t2?)=E{[X(t1?)?μX?(t1?)][X(t2?)?μX?(t2?)]}

References

[1] 十三、梯度下降方法对比
[2] 机器学习方法（一）——梯度下降法
[3] 机器学习（四）：批量梯度下降法（BGD）、随机梯度下降法（SGD）和小批量梯度下降法（MBGD）
[4] 如何理解“梯度下降法”？什么是“反向传播”？通过一个视频，一步一步全部搞明白
[5]期望、方差、协方差、协方差函数、期望函数、方差函数
[6]协方差与相关系数
[7]高斯过程-百度百科
[8]箱型图
[9]深度学习优化函数详解（4）-- momentum 动量法
[10]深度学习最优化（四）—— 动量法/Nesterov/Adagrad/Adadelta/RMSprop/Adam/Nadam
[11]adam和adamW