LSTM
Understanding LSTM Networks 和 人人都能看懂的LSTM 这两篇文章介绍了 LSTM 的原理。
2D-LSTM
2D-LSTM 是作用于三维输入(
W
×
H
×
D
W \times H \times D
W×H×D )的 LSTM ,分别取横向和纵向上一时刻的隐藏状态和输出作为该时刻的输入,如下图所示
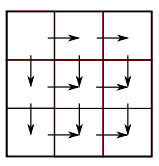
数据传播的顺序依靠对角线原则,如下图所示
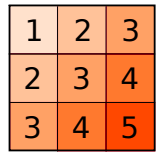
图中的数字表示计算的顺序。
下图展示了 2D-LSTM 单元的结构,蓝线表示与标准单元不同的地方。

上图中
x
j
,
i
x_{j, i}
xj,i? 为当前的输入,
s
j
,
i
?
1
s_{j, i-1}
sj,i?1? 为上一时刻横向的输出,
s
j
?
1
,
i
s_{j-1, i}
sj?1,i? 为上一时刻纵向的输出。
input gate
i
j
,
i
=
σ
(
W
1
x
j
,
i
+
U
1
s
j
?
1
,
i
+
V
1
s
j
,
i
?
1
)
i_{j, i} = \sigma(W_1x_{j, i} + U_1s_{j-1, i} + V_1s_{j, i-1})
ij,i?=σ(W1?xj,i?+U1?sj?1,i?+V1?sj,i?1?)
output gate
o
j
,
i
=
σ
(
W
2
x
j
,
i
+
U
2
s
j
?
1
,
i
+
V
2
s
j
,
i
?
1
)
o_{j, i} = \sigma(W_2x_{j, i} + U_2s_{j-1, i} + V_2s_{j, i-1})
oj,i?=σ(W2?xj,i?+U2?sj?1,i?+V2?sj,i?1?)
candidate value
c
^
j
,
i
=
g
(
W
3
x
j
,
i
+
U
3
s
j
?
1
,
i
+
V
3
s
j
,
i
?
1
)
\hat{c}_{j, i} = g(W_3x_{j, i} + U_3s_{j-1, i} + V_3s_{j, i-1})
c^j,i?=g(W3?xj,i?+U3?sj?1,i?+V3?sj,i?1?)
forget gate
f
j
,
i
=
σ
(
W
4
x
j
,
i
+
U
4
s
j
?
1
,
i
+
V
4
s
j
,
i
?
1
)
f_{j, i} = \sigma(W_4x_{j, i} + U_4s_{j-1, i} + V_4s_{j, i-1})
fj,i?=σ(W4?xj,i?+U4?sj?1,i?+V4?sj,i?1?)
2D-LSTM 新加入了一个系数,用于比较
s
j
?
1
,
i
s_{j-1, i}
sj?1,i? 和
s
j
,
i
?
1
s_{j, i-1}
sj,i?1? 的重要程度。
λ
j
,
i
=
σ
(
W
5
x
j
,
i
+
U
5
s
j
?
1
,
i
+
V
5
s
j
,
i
?
1
)
\lambda_{j, i} = \sigma(W_5x_{j, i} + U_5s_{j-1, i} + V_5s_{j, i-1})
λj,i?=σ(W5?xj,i?+U5?sj?1,i?+V5?sj,i?1?)
新状态
c
j
,
i
=
f
j
,
i
°
[
λ
j
,
i
°
c
j
?
1
,
i
+
(
1
?
λ
j
,
i
)
°
c
j
,
i
?
1
]
+
c
^
j
,
i
°
i
j
,
i
c_{j, i} = f_{j, i} \circ [\lambda_{j, i} \circ c_{j-1, i} + (1 - \lambda_{j, i}) \circ c_{j, i-1}] + \hat{c}_{j, i} \circ i_{j, i}
cj,i?=fj,i?°[λj,i?°cj?1,i?+(1?λj,i?)°cj,i?1?]+c^j,i?°ij,i?
输出
s
j
,
i
=
g
(
c
j
,
i
°
o
j
,
i
)
s_{j, i} = g(c_{j, i} \circ o_{j, i})
sj,i?=g(cj,i?°oj,i?)
Reference
[1] Bahar, P. , C. Brix , and H. Ney . “Towards Two-Dimensional Sequence to Sequence Model in Neural Machine Translation.” (2018).
[2] Voigtlaender, P. , P. Doetsch , and H. Ney . “Handwriting Recognition with Large Multidimensional Long Short-Term Memory Recurrent Neural Networks.” 2016 15th International Conference on Frontiers in Handwriting Recognition (ICFHR) IEEE, 2017.