[人工智能]基于LibSVM得到决策函数

下载

LibSVM

解压

导入

我用的是Java，所以导入Java文件夹下的所有文件

数据准备

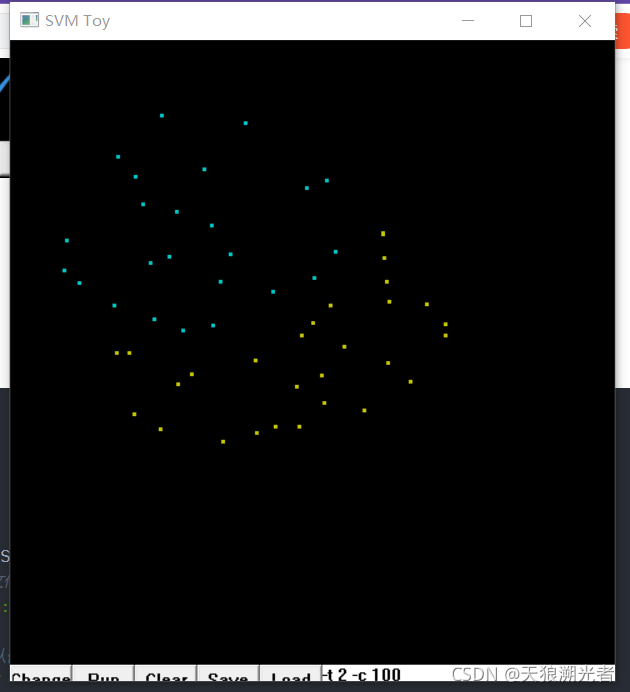
训练

public class Main {

    public static void main(String[] args) throws IOException {
	// write your code here

        //存放数据以及保存模型文件路径
        String filepath = "F:\\LibSVM\\src\\test\\";
        /**
         * -s 设置svm类型：默认值为0
         *          0– C-SVC
         *          1 – v-SVC
         *          2 – one-class-SVM
         *          3 –ε-SVR
         *          4 – n - SVR
         *
         * -t 设置核函数类型，默认值为2
         *          0 --线性核
         *          1 --多项式核
         *          2 -- RBF核
         *          3 -- sigmoid核
         *
         * -d degree:设置多项式核中degree的值，默认为3
         *
         * -c cost：设置C-SVC、ε-SVR、n - SVR中从惩罚系数C，默认值为1；
         */
        String[] arg = {"-s","0","-c","10","-t","0",filepath+"data.txt",filepath+"line.txt"};
        System.out.println("----------------线性-----------------");
        //训练函数
        svm_train.main(arg);

        arg[5]="1";
        arg[7]=filepath+"poly.txt";//输出文件路径
        System.out.println("---------------多项式-----------------");
        svm_train.main(arg);

        arg[5]="2";
        arg[7]=filepath+"RBF.txt";
        System.out.println("---------------高斯核-----------------");
        svm_train.main(arg);
    }
}

结果

----------------线性-----------------
*
optimization finished, #iter = 23
nu = 0.4134829716154515
obj = -178.54389750792222, rho = -4.995583270297827
nSV = 24, nBSV = 22
Total nSV = 24
---------------多项式-----------------
*
optimization finished, #iter = 22
nu = 0.8148148148148148
obj = -333.8885933617712, rho = -1.1244767460448202
nSV = 44, nBSV = 44
Total nSV = 44
---------------高斯核-----------------
*
optimization finished, #iter = 25
nu = 0.418841415957994
obj = -178.03351240376924, rho = 1.2515298599821647
nSV = 25, nBSV = 22
Total nSV = 25

Process finished with exit code 0

• data.txt 训练数据
• line.txt 线性模型
• poly.txt多项式模型
• RBF.txt 高斯核模型

文件数据

• svm_type
  所选择的svm类型，默认为c_svc
• kernel_type
  训练采用的核函数类型，此处为RBF核
• gamma
  RBF核的参数γ
• nr_class
  类别数
• total_sv
  支持向量总个数
• rho
  判决函数的偏置项b
• label
  原始文件中的类别标识
• nr_sv
  每个类的支持向量机的个数
• SV
  各个类的权系数及相应的支持向量
  
  
  

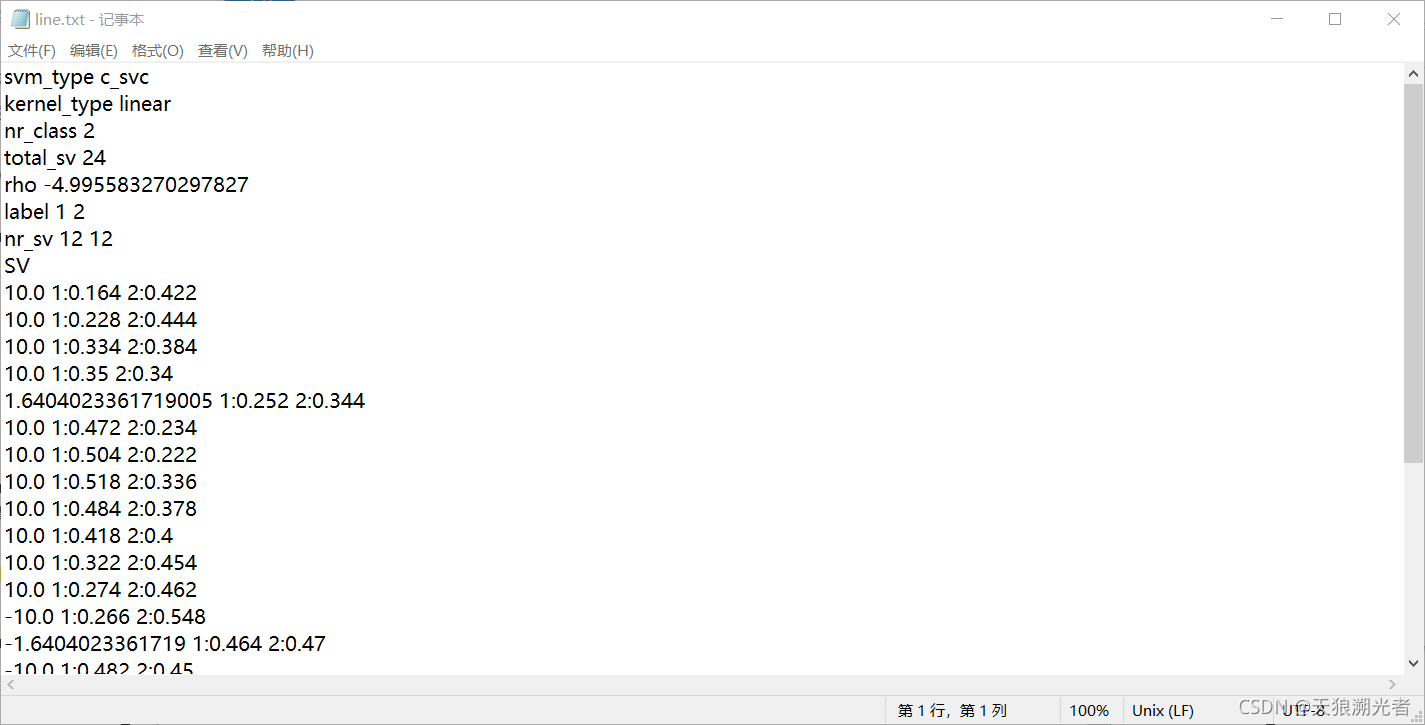
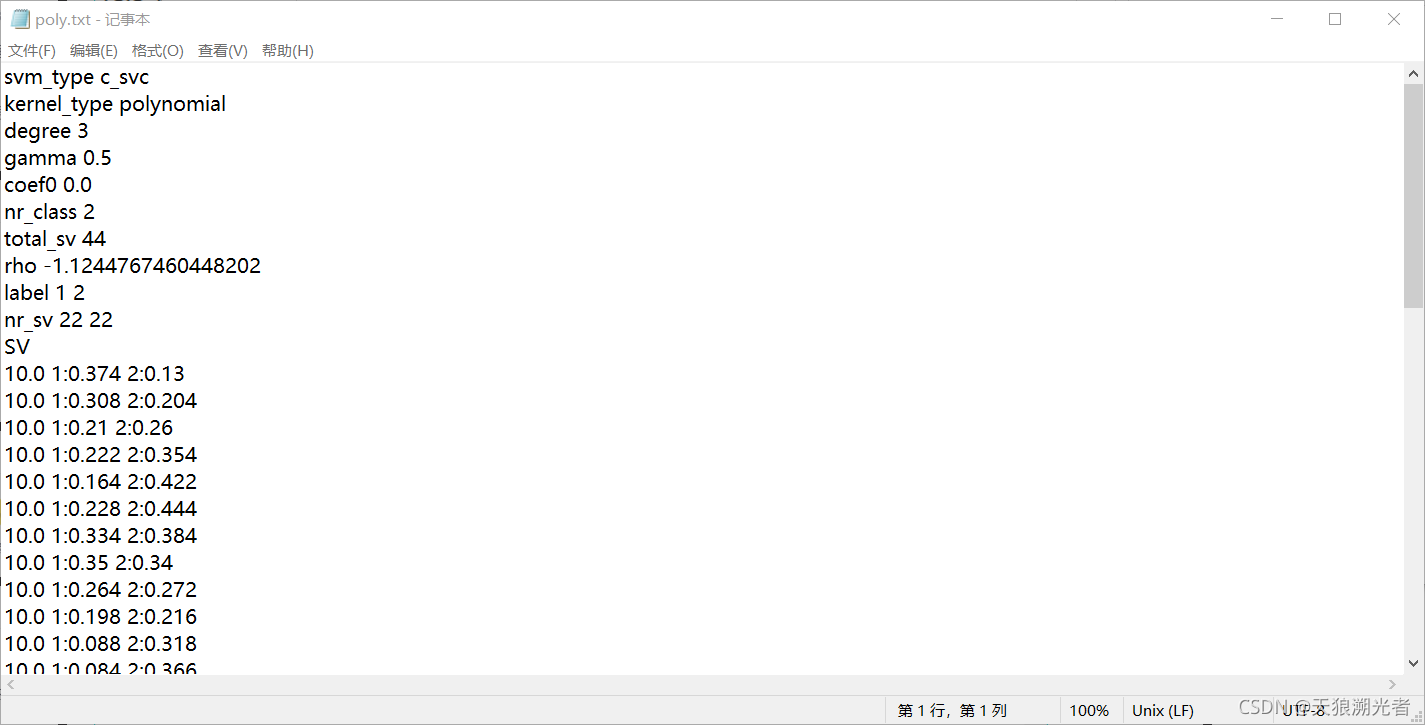
决策函数

根据公式f(x)=wT*x+b以及模型数据可以求得最终的决策函数。

参考资料

• 基于LibSVM得到决策函数