[人工智能]深度学习入门系列20：LSTM递归神经网络解决国际航空乘客预测问题

大家好，我技术人Howzit，这是深度学习入门系列第二十篇，欢迎大家一起交流！

深度学习入门系列1：多层感知器概述
深度学习入门系列2：用TensorFlow构建你的第一个神经网络
深度学习入门系列3：深度学习模型的性能评价方法
深度学习入门系列4：用scikit-learn找到最好的模型
深度学习入门系列5项目实战：用深度学习识别鸢尾花种类
深度学习入门系列6项目实战：声纳回声识别
深度学习入门系列7项目实战：波士顿房屋价格回归
深度学习入门系列8：用序列化保存模型便于继续训练
深度学习入门系列9：用检查点保存训练期间最好的模型
深度学习入门系列10：从绘制记录中理解训练期间的模型行为
深度学习入门系列11：用Dropout正则减少过拟合
深度学习入门系列12：使用学习规划来提升性能
深度学习入门系列13：卷积神经网络概述
深度学习入门系列14：项目实战：基于CNN的手写数字识别
深度学习入门系列15：用图像增强改善模型性能
深度学习入门系列16：项目实战：图像中目标识别
深度学习入门系列17：项目实战：从电影评论预测情感
深度学习入门系列18：递归神经网络概述
深度学习入门系列19：基于窗口（window）的多层感知器解决时序问题
深度学习入门系列20：LSTM递归神经网络解决国际航空乘客预测问题
待更新……
深度学习入门系列21：理解LSTM递归神经网络
深度学习入门系列22：项目：用爱丽丝梦游仙境生成文本

时序预测问题是预测建模问题中的一个难点，不像回归预测那样，在输入变量中，时序也增加了序列中依赖的复杂性。有一种强大的神经网络专门处理时序依赖问题，我们称之为递归神经网络**（RNN）。LSTM就是递归神经网络的一种，它能成功在深度学习中应用，主要是因为它的结构能够成功被训练。在这节课中，你将学习如何通过Keras深度学习库开发LSTM网络来解决时序预测问题。完成本节课之后，你了解如何实现和开发LSTM**网络来解决自己的时序问题以及其他的时序问题。

你将了解：

• 如何开发LSTM网络，把时序预测问题转述为回归问题。
• 针对时序问题使用窗口(window)和时间步（time step） 来开发 LSTM 网络。
• 在非常长序列中，如何使用保存了状态的LSTM网络进行开发和做预测。

对于标准的时序预测问题，我们将开发多个 LSTM 神经单元。下面的问题和所选择的配置都是为了说明问题，并不最优的。下面的例子正式的介绍如何开发属于自己的LSTM神经网络并解决时序预测问题。

让我们开始吧。

1 LSTM网络用于回归

在上节中的国际航空乘客预测问题在这节课会重新思考一下，我们够将问题转述为回归问题，正如在上节课做的那样。换句话说，给定这个月乘客数量，得出下个月的乘客数量（单位为1000）。这个例子会复用上节课数据加载和数据预处理。特别是create_data() 函数。

LSTMs 神经网络对数据大小比较敏感，特别是使用 sigmoid（默认）和 tanh 激活函数。把数据规整在0-1之间，我们称之为正则化。我们能够通过来自 scikit-learn 库中的MinMaxScaler preprocessing来正则化数据。

# normalize the dataset 
scaler = MinMaxScaler(feature_range=(0, 1)) 
dataset = scaler.fit_transform(dataset)

LSTM网络期望的输入数据**（X）** 是指定的某个格式：[samples,time steps,features]，我们预处理的数据形式为：[samples,features] ，对于每个样本我们将问题定义为时间步长。我们使用numpy.reshape() 可以把我们预处理的训练集和测试集转成我们期望的结构：

# reshape input to be [samples, time steps, features] 
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1])) 
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))

我们现在准备为整个问题设计并拟合我们的 LSTM 网络。这个网络拥有一个输入神经元的输入层，带有四个LSTM单元隐藏层以及预测一个输出值的输出层。在LSTM记忆单元中使用默认激活函数sigmoid，这个网络训练100次而且使用批处理大小为1。

# create and fit the LSTM network 
model = Sequential() 
model.add(LSTM(4, input_shape=(1, look_back)))
model.add(Dense(1)) 
model.compile(loss='mean_squared_error', optimizer='adam') 
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)

为了完整性，下面是整个代码。

# LSTM for international airline passengers problem with regression framing  
import math  
  
import matplotlib.pyplot as plt  
import numpy  
from keras.layers import Dense  
from keras.layers import LSTM  
from keras.models import Sequential  
from pandas import read_csv  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
  
  
# convert an array of values into a dataset matrix  
def create_dataset(dataset, look_back=1):  
    dataX, dataY = [], []  
    for i in range(len(dataset) - look_back - 1):  
        a = dataset[i:(i + look_back), 0]  
        dataX.append(a)  
        dataY.append(dataset[i + look_back, 0])  
    return numpy.array(dataX), numpy.array(dataY)  
  
  
# fix random seed for reproducibility  
numpy.random.seed(7)  

# load the dataset  
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',  
                     skipfooter=3)  
dataset = dataframe.values  
dataset = dataset.astype('float32')  

# normalize the dataset  
scaler = MinMaxScaler(feature_range=(0, 1))  
dataset = scaler.fit_transform(dataset)  

# split into train and test sets  
train_size = int(len(dataset) * 0.67)  
test_size = len(dataset) - train_size  
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]  

# reshape into X=t and Y=t+1  
look_back = 1  
trainX, trainY = create_dataset(train, look_back)  
testX, testY = create_dataset(test, look_back)  

# reshape input to be [samples, time steps, features]  
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))  
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))  

# create and fit the LSTM network  
model = Sequential()  
model.add(LSTM(4, input_shape=(1, look_back)))  
model.add(Dense(1))  
model.compile(loss='mean_squared_error', optimizer='adam')  
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)  

# make predictions  
trainPredict = model.predict(trainX)  
testPredict = model.predict(testX)  

# invert predictions  
trainPredict = scaler.inverse_transform(trainPredict)  
trainY = scaler.inverse_transform([trainY])  
testPredict = scaler.inverse_transform(testPredict)  
testY = scaler.inverse_transform([testY])  

# calculate root mean squared error  
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:, 0]))  
print('Train Score: %.2f RMSE' % (trainScore))  
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:, 0]))  
print('Test Score: %.2f RMSE' % (testScore))  

# shift train predictions for plotting  
trainPredictPlot = numpy.empty_like(dataset)  
trainPredictPlot[:, :] = numpy.nan  
trainPredictPlot[look_back:len(trainPredict) + look_back, :] = trainPredict  

# shift test predictions for plotting  
testPredictPlot = numpy.empty_like(dataset)  
testPredictPlot[:, :] = numpy.nan  
testPredictPlot[len(trainPredict) + (look_back * 2) + 1:len(dataset) - 1, :] = testPredict  

# plot baseline and predictions  
plt.plot(scaler.inverse_transform(dataset))  
plt.plot(trainPredictPlot)  
plt.plot(testPredictPlot)  
plt.show()

运行这个模型，得到如下的结果：

Epoch 96/100
 - 0s - loss: 0.0020
Epoch 97/100
 - 0s - loss: 0.0019
Epoch 98/100
 - 0s - loss: 0.0019
Epoch 99/100
 - 0s - loss: 0.0019
Epoch 100/100
 - 0s - loss: 0.0019
Train Score: 22.34 RMSE
Test Score: 45.89 RMSE

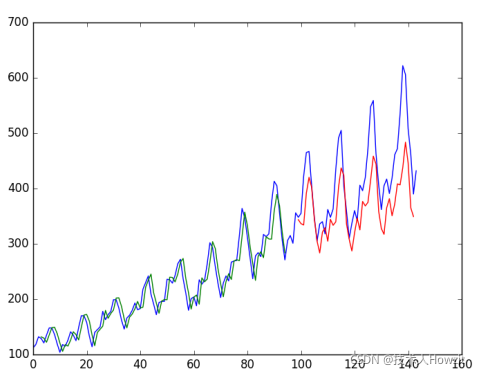
我们能够看到，模型在训练集和测试集上的拟合的结果是不错的。

我们能够看到，模型在训练集得到23个乘客的误差（单位1000），在测试集上得到52个误差，也不算差。

2 使用窗口（Window）方法的LSTM回归

我们也能重述这个问题以至于多个时间步能够对下一时间预测，称之为窗口，其大小是根据问题而设置的。例如，给定当前时间**（t）** ，我们想在序列中预测下个时间**（t+1）** 的值，我们能够使用当前时间（t）和前两个时间（t-1和t-2） 作为输入变量。当问题转述为回归问题时，其输入变量为t-2，t-1，t和输出变量t+1。

上节课创建的 create_dataset() 函数，允许我们将 look_back 参数从1增加为3来创建时序问题格式。数据集的样例格式如下：

X1   X2  X3  Y 
112 118 132 129 
118 132 129 121 
132 129 121 135 
129 121 135 148 
121 135 148 148

我们重新运行了上节课大窗口的例子，为了完整性，我们将大尺寸窗口的整个代码放在下面：

# LSTM for international airline passengers problem with window regression framing  

import math  
  
import matplotlib.pyplot as plt  
import numpy  
from keras.layers import Dense  
from keras.layers import LSTM  
from keras.models import Sequential  
from pandas import read_csv  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
  
  
# convert an array of values into a dataset matrix  
def create_dataset(dataset, look_back=1):  
    dataX, dataY = [], []  
    for i in range(len(dataset) - look_back - 1):  
        a = dataset[i:(i + look_back), 0]  
        dataX.append(a)  
        dataY.append(dataset[i + look_back, 0])  
    return numpy.array(dataX), numpy.array(dataY)  
  
  
# fix random seed for reproducibility  
numpy.random.seed(7)  
# load the dataset  
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',  
                     skipfooter=3)  
dataset = dataframe.values  
dataset = dataset.astype('float32')  
# normalize the dataset  
scaler = MinMaxScaler(feature_range=(0, 1))  
dataset = scaler.fit_transform(dataset)  
# split into train and test sets  
train_size = int(len(dataset) * 0.67)  
test_size = len(dataset) - train_size  
  
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]  

# reshape into X=t and Y=t+1  
look_back = 3  
trainX, trainY = create_dataset(train, look_back)  
testX, testY = create_dataset(test, look_back)  

# reshape input to be [samples, time steps, features]  
trainX = numpy.reshape(trainX, (trainX.shape[0], 1, trainX.shape[1]))  
testX = numpy.reshape(testX, (testX.shape[0], 1, testX.shape[1]))  

# create and fit the LSTM network  
model = Sequential()  
model.add(LSTM(4, input_shape=(1, look_back)))  
model.add(Dense(1))  
model.compile(loss='mean_squared_error', optimizer='adam')  
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)  

# make predictions  
trainPredict = model.predict(trainX)  
testPredict = model.predict(testX)  

# invert predictions  
trainPredict = scaler.inverse_transform(trainPredict)  
trainY = scaler.inverse_transform([trainY])  
testPredict = scaler.inverse_transform(testPredict)  
testY = scaler.inverse_transform([testY])  

# calculate root mean squared error  
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:, 0]))  
print('Train Score: %.2f RMSE' % (trainScore))  
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:, 0]))  
print('Test Score: %.2f RMSE' % (testScore))  

# shift train predictions for plotting  
trainPredictPlot = numpy.empty_like(dataset)  
trainPredictPlot[:, :] = numpy.nan  
trainPredictPlot[look_back:len(trainPredict) + look_back, :] = trainPredict  

# shift test predictions for plotting  
testPredictPlot = numpy.empty_like(dataset)  
testPredictPlot[:, :] = numpy.nan  
testPredictPlot[len(trainPredict) + (look_back * 2) + 1:len(dataset) - 1, :] = testPredict  

# plot baseline and predictions  
plt.plot(scaler.inverse_transform(dataset))  
plt.plot(trainPredictPlot)  
plt.plot(testPredictPlot)  
plt.show()

运行上面例子得到下面的输出结果。

... 
Epoch 95/100 0s - loss: 0.0021 
Epoch 96/100 0s - loss: 0.0021 
Epoch 97/100 0s - loss: 0.0021 
Epoch 98/100 0s - loss: 0.0021 
Epoch 99/100 0s - loss: 0.0022 
Epoch 100/100 0s - loss: 0.0020 
Train Score: 24.19 RMSE 
Test Score: 58.03 RMSE

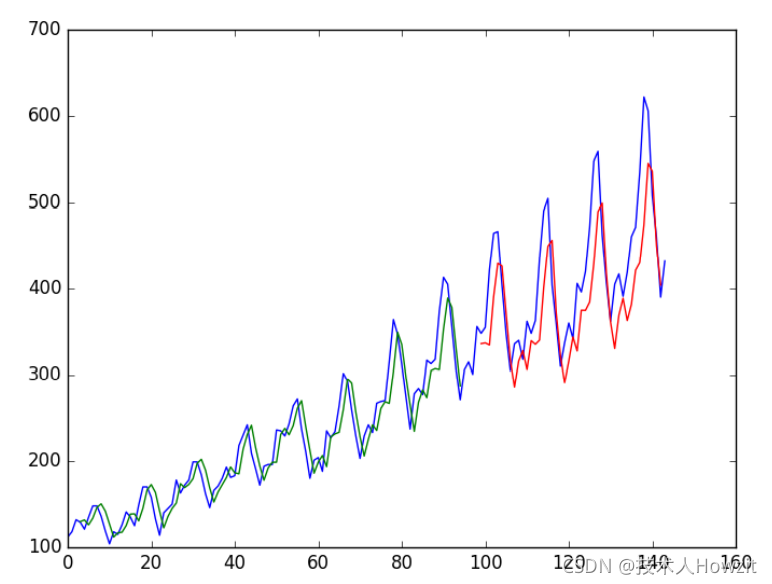
我们能够看到和上节课中的相比错误略有增加。窗口的大小和网络接口并没有调节，只是展示如何解决预测问题。

3 LSTM For Regression with Time Steps

你可能已经注意到，对于LSTM网络的数据预处理包括时间步长。有一些时序问题可能有不同的时间步长。例如，你已经有了导致失败点和点聚集的物理机器测量数据。每个事故是个样本，那么出现事故的观察值作为时间步，被观察的变量为特征。时间步长提供另外一种陈述时序问题的方法。像上面窗口的例子，我们把序列中的前时间步作为输入值来预测下个时间的输出值。

相反，我们把过去的观察值作为单独输出特征，这样的话，我们就能把一个输出特征作为一个时间步长，这样的确是一个更为准确问题架构。我们也能够在前面基于窗口的例子中使用同样的数据表示来这么做，除非当我们重整数据，那么我们设置这个列为时间步长维度，并且改变特征维度为1.例如：

# reshape input to be [samples, time steps, features] 
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1)) 
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))

为了完整性，下面列出了整个代码。

# LSTM for international airline passengers problem with time step regression framing  
import math  
  
import matplotlib.pyplot as plt  
import numpy  
from keras.layers import Dense  
from keras.layers import LSTM  
from keras.models import Sequential  
from pandas import read_csv  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
  
  
# convert an array of values into a dataset matrix  
def create_dataset(dataset, look_back=1):  
    dataX, dataY = [], []  
    for i in range(len(dataset) - look_back - 1):  
        a = dataset[i:(i + look_back), 0]  
        dataX.append(a)  
        dataY.append(dataset[i + look_back, 0])  
    return numpy.array(dataX), numpy.array(dataY)  
  
  
# fix random seed for reproducibility  
numpy.random.seed(7)  
# load the dataset  
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',  
                     skipfooter=3)  
dataset = dataframe.values  
dataset = dataset.astype('float32')  
# normalize the dataset  
scaler = MinMaxScaler(feature_range=(0, 1))  
dataset = scaler.fit_transform(dataset)  
# split into train and test sets  
train_size = int(len(dataset) * 0.67)  
test_size = len(dataset) - train_size  
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]  
# reshape into X=t and Y=t+1  
look_back = 3  
trainX, trainY = create_dataset(train, look_back)  
testX, testY = create_dataset(test, look_back)  
# reshape input to be [samples, time steps, features]  
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))  
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))  
# create and fit the LSTM network  
model = Sequential()  
model.add(LSTM(4, input_shape=(look_back, 1)))  
model.add(Dense(1))  
model.compile(loss='mean_squared_error', optimizer='adam')  
model.fit(trainX, trainY, epochs=100, batch_size=1, verbose=2)  
  
# make predictions  
trainPredict = model.predict(trainX)  
testPredict = model.predict(testX)  
  
# invert predictions  
trainPredict = scaler.inverse_transform(trainPredict)  
trainY = scaler.inverse_transform([trainY])  
testPredict = scaler.inverse_transform(testPredict)  
testY = scaler.inverse_transform([testY])  
  
# calculate root mean squared error  
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:, 0]))  
print('Train Score: %.2f RMSE' % (trainScore))  
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:, 0]))  
print('Test Score: %.2f RMSE' % (testScore))  
  
# shift train predictions for plotting  
trainPredictPlot = numpy.empty_like(dataset)  
trainPredictPlot[:, :] = numpy.nan  
trainPredictPlot[look_back:len(trainPredict) + look_back, :] = trainPredict  
  
# shift test predictions for plotting  
testPredictPlot = numpy.empty_like(dataset)  
testPredictPlot[:, :] = numpy.nan  
testPredictPlot[len(trainPredict) + (look_back * 2) + 1:len(dataset) - 1, :] = testPredict  
  
# plot baseline and predictions  
plt.plot(scaler.inverse_transform(dataset))  
plt.plot(trainPredictPlot)  
plt.plot(testPredictPlot)  
plt.show()

运行上面的代码，得到下面的结果：

... 
Epoch 95/100 1s - loss: 0.0021 
Epoch 96/100 1s - loss: 0.0021 
Epoch 97/100 1s - loss: 0.0021 
Epoch 98/100 1s - loss: 0.0020 
Epoch 99/100 1s - loss: 0.0021 
Epoch 100/100 1s - loss: 0.0020 

Train Score: 23.69 RMSE 
Test Score: 58.88 RMSE

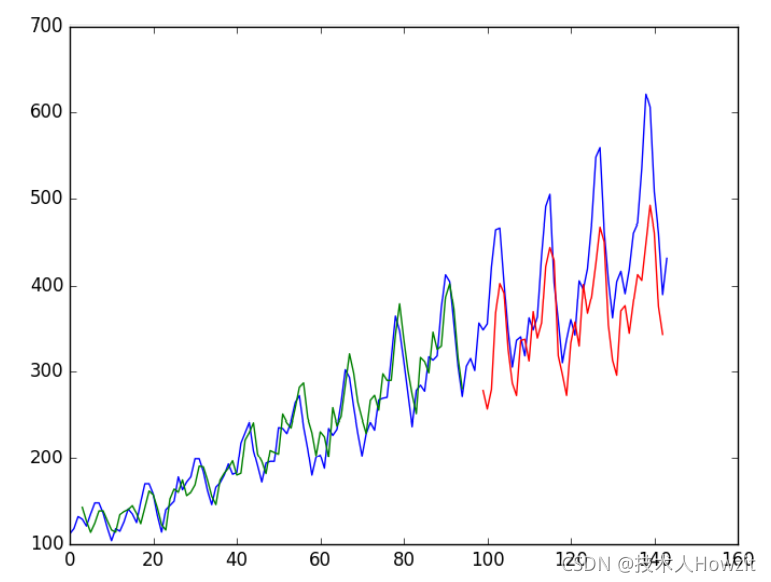
我们能够看到结果要比上个例子稍微好点，是输入数据的结构起了作用。

4 LSTM With Memory Between Batches.

LSTM 网络具有记忆功能，它能够记住整个长的序列。正常来说，拟合模型时，每次批处理训练后，网络内的状态会重置，每次也会调用model.predict() 或者 model.evaluate()。当我LSTM网络在Keras中被清除时，我们能够让LSTM层有状态来获得更加精准的控制。这就意味着他能够随着整个训练序列构来建状态，而且还能在我们需要的做预测时维持那个状态。

这需要当我们拟合网络时训练集不能打乱，它也需要每次暴露训练集后通过调model.reset_states() 函数显性重置网络状态。这就意味着在调 model.fit() 和 model.reset_states() 必须创建自己的外迭代循环。举个例子：

for i in range(100): 
	model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)
	model.reset_states()

最后，当LSTM 层构建好，stateful参数必须设置为True，不用指定输入维度，我们通过batch_input_shape参数传入批处理样本数量，样本的时间步数量和时间步中的特征数量。举个例子：

model.add(LSTM(4, batch_input_shape=(batch_size, time_steps, features), stateful=True))

当我们评估模型和做预测时，必须使用同样的批处理大小。例如：

model.predict(trainX, batch_size=batch_size)

先前的时间步长的例子适用于有状态的LSTM，下面提供按了完整的代码。

# LSTM for international airline passengers problem with memory  
import math  
  
import matplotlib.pyplot as plt  
import numpy  
from keras.layers import Dense  
from keras.layers import LSTM  
from keras.models import Sequential  
from pandas import read_csv  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
  
  
# convert an array of values into a dataset matrix  
def create_dataset(dataset, look_back=1):  
    dataX, dataY = [], []  
    for i in range(len(dataset) - look_back - 1):  
        a = dataset[i:(i + look_back), 0]  
        dataX.append(a)  
        dataY.append(dataset[i + look_back, 0])  
    return numpy.array(dataX), numpy.array(dataY)  
  
  
# fix random seed for reproducibility  
numpy.random.seed(7)  
# load the dataset  
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',  
                     skipfooter=3)  
dataset = dataframe.values  
dataset = dataset.astype('float32')  
# normalize the dataset  
scaler = MinMaxScaler(feature_range=(0, 1))  
dataset = scaler.fit_transform(dataset)  
# split into train and test sets  
train_size = int(len(dataset) * 0.67)  
test_size = len(dataset) - train_size  
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]  
# reshape into X=t and Y=t+1  
look_back = 3  
trainX, trainY = create_dataset(train, look_back)  
testX, testY = create_dataset(test, look_back)  
# reshape input to be [samples, time steps, features]  
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))  
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))  
# create and fit the LSTM network  
  
batch_size = 1  
model = Sequential()  
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))  
model.add(Dense(1))  
model.compile(loss='mean_squared_error', optimizer='adam')  
for i in range(100):  
    model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)  
    model.reset_states()  
# make predictions  
trainPredict = model.predict(trainX, batch_size=batch_size)  
model.reset_states()  
testPredict = model.predict(testX, batch_size=batch_size)  
# invert predictions  
trainPredict = scaler.inverse_transform(trainPredict)  
trainY = scaler.inverse_transform([trainY])  
testPredict = scaler.inverse_transform(testPredict)  
testY = scaler.inverse_transform([testY])  
# calculate root mean squared error  
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:, 0]))  
print('Train Score: %.2f RMSE' % (trainScore))  
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:, 0]))  
print('Test Score: %.2f RMSE' % (testScore))  
# shift train predictions for plotting  
trainPredictPlot = numpy.empty_like(dataset)  
trainPredictPlot[:, :] = numpy.nan  
trainPredictPlot[look_back:len(trainPredict) + look_back, :] = trainPredict  
# shift test predictions for plotting  
testPredictPlot = numpy.empty_like(dataset)  
testPredictPlot[:, :] = numpy.nan  
testPredictPlot[len(trainPredict) + (look_back * 2) + 1:len(dataset) - 1, :] = testPredict  
# plot baseline and predictions  
plt.plot(scaler.inverse_transform(dataset))  
plt.plot(trainPredictPlot)  
plt.plot(testPredictPlot)  
plt.show()

运行上面代码，得到如下结果：

... 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0016 

Train Score: 20.74 RMSE 
Test Score: 52.23 RMSE

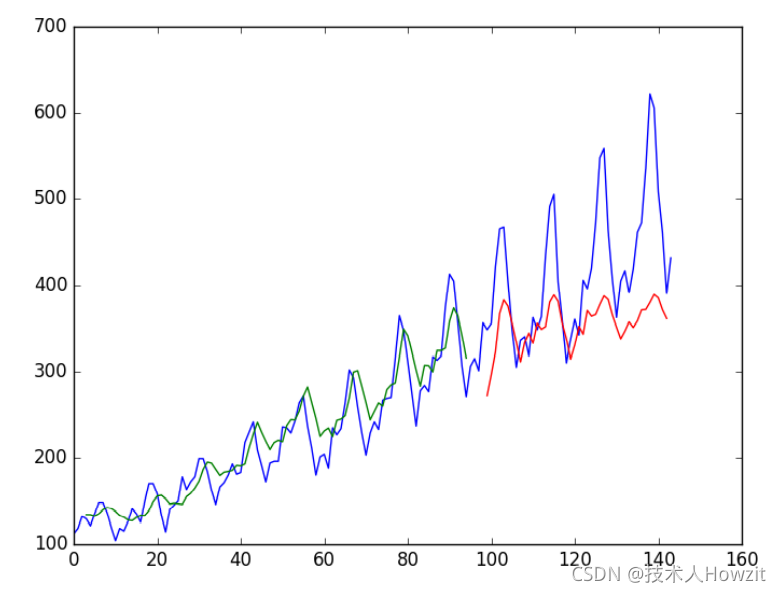
我们能够看出，结果比有些好，比其他的有点差，模型需要更多的模块，可能还需要更多迭代周期来内化一些结构的问题。

5 Stacked LSTMs With Memory Between Batches

最后，我们将要看看大型LSTM的优点之一，当他嵌入深度网络结构中时，它们能够成功的训练。LSTM网络在Keras中用同样的方法嵌入进去，其他类型的层也能嵌入进去。另外一个必要的配置是在LSTM层之前的LSTM层必须返回这个序列，可以在层中设置return_sequences参数为True。在上个部分，我们扩展了有状态的LSTM，它有两层，如下：

model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True, return_sequences=True)) 
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))

为了完整性，整个代码在下面给出来了。

# Stacked LSTM for international airline passengers problem with memory  
import math  
  
import matplotlib.pyplot as plt  
import numpy  
from keras.layers import Dense  
from keras.layers import LSTM  
from keras.models import Sequential  
from pandas import read_csv  
from sklearn.metrics import mean_squared_error  
from sklearn.preprocessing import MinMaxScaler  
  
  
# convert an array of values into a dataset matrix  
def create_dataset(dataset, look_back=1):  
    dataX, dataY = [], []  
    for i in range(len(dataset) - look_back - 1):  
        a = dataset[i:(i + look_back), 0]  
        dataX.append(a)  
        dataY.append(dataset[i + look_back, 0])  
    return numpy.array(dataX), numpy.array(dataY)  
  
  
# fix random seed for reproducibility  
numpy.random.seed(7)  

# load the dataset  
dataframe = read_csv('international-airline-passengers.csv', usecols=[1], engine='python',  
                     skipfooter=3)  
dataset = dataframe.values  
dataset = dataset.astype('float32')  

# normalize the dataset  
scaler = MinMaxScaler(feature_range=(0, 1))  
dataset = scaler.fit_transform(dataset)  

# split into train and test sets  
train_size = int(len(dataset) * 0.67)  
test_size = len(dataset) - train_size  
train, test = dataset[0:train_size, :], dataset[train_size:len(dataset), :]  

# reshape into X=t and Y=t+1  
look_back = 3  
trainX, trainY = create_dataset(train, look_back)  
testX, testY = create_dataset(test, look_back)  
# reshape input to be [samples, time steps, features]  
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], 1))  
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], 1))  

# create and fit the LSTM network  
batch_size = 1  
model = Sequential()  
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True,  
               return_sequences=True))  
model.add(LSTM(4, batch_input_shape=(batch_size, look_back, 1), stateful=True))  
model.add(Dense(1))  
model.compile(loss='mean_squared_error', optimizer='adam')  
for i in range(100):  
    model.fit(trainX, trainY, epochs=1, batch_size=batch_size, verbose=2, shuffle=False)  
model.reset_states()  

# make predictions  
trainPredict = model.predict(trainX, batch_size=batch_size)  
model.reset_states()  
testPredict = model.predict(testX, batch_size=batch_size)  
# invert predictions  
trainPredict = scaler.inverse_transform(trainPredict)  
trainY = scaler.inverse_transform([trainY])  
testPredict = scaler.inverse_transform(testPredict)  
testY = scaler.inverse_transform([testY])  

# calculate root mean squared error  
trainScore = math.sqrt(mean_squared_error(trainY[0], trainPredict[:, 0]))  
print('Train Score: %.2f RMSE' % (trainScore))  
testScore = math.sqrt(mean_squared_error(testY[0], testPredict[:, 0]))  
print('Test Score: %.2f RMSE' % (testScore))  

# shift train predictions for plotting  
trainPredictPlot = numpy.empty_like(dataset)  
trainPredictPlot[:, :] = numpy.nan  
trainPredictPlot[look_back:len(trainPredict) + look_back, :] = trainPredict  

# shift test predictions for plotting  
testPredictPlot = numpy.empty_like(dataset)  
testPredictPlot[:, :] = numpy.nan  
testPredictPlot[len(trainPredict) + (look_back * 2) + 1:len(dataset) - 1, :] = testPredict  

# plot baseline and predictions  
plt.plot(scaler.inverse_transform(dataset))  
plt.plot(trainPredictPlot)  
plt.plot(testPredictPlot)  
plt.show()

运行上面代码，得到如下结果：

... 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0017 
Epoch 1/1 1s - loss: 0.0016 

Train Score: 20.49 RMSE
Test Score: 56.35 RMSE

在数据集上的预测再一次变糟。再一次证据表明我们需要额外的训练周期。

总结

在这节课中，你已经学习了如何开发LSTM递归神经网络解决时序问题。特别是，你已经学到了：关于国际航空乘客的时序预测问题。

• 如何为回归问题和时序问题的窗口格式创建一个LSTM。
• 如何用时序问题的时间步形式创建LSTM。
• 如何用状态和嵌入带有状态的LSTM单元创建LSTM网络学习长时序。

下一步

在这节课中，你已经学习了如何使用LSTM递归神经网络解决时序预测问题，接下来，你将用发现LSTM网络的新技能，解决时序分类问题。