[人工智能]【论文阅读】Self-supervised Learning on Graphs:Deep Insights and New Directions

论文地址：https://arxiv.org/abs/2006.10141
代码地址: https://github.com/ChandlerBang/SelfTask-GNN

0 摘要

GNN可以通过简单的邻域聚合自然地利用未标记的节点，而邻域聚合无法彻底利用未标记的节点。

本文：

• 我们首先通过实证研究图上的许多基本SSL辅助任务，加深了我们对SSL何时、为何以及哪些策略对GNN有效的理解。
• 受到实证研究的深刻见解的启发，我们提出了一个新方向 SelfTask 来构建能够在各种真实世界数据集上实现最先进性能的高级借口任务。

2 问题描述

半监督节点分类将节点分为有标签节点${\mathcal{D}}_L=({\mathcal{V}}_L,{\mathcal{Y}}_L)$和无标签节点${\mathcal{D}}_U$。让$f_{\theta }:{\mathcal{V}}_L\to {\mathcal{Y}}_L$，将节点映射到标签集，使得GNN可以推断出未标记数据的特征。半监督节点分类的目标函数是：

$$\underset{\theta }{\min }{\mathcal{L}}_{task}(\theta ,A,X,{\mathcal{D}}_L)=\sum _{(v_i,y_i)\in {\mathcal{D}}_L}l(f_{\theta }(\mathcal{G}{)}_{v_i},y_i)$$

我们将图神经网络的自我监督学习问题正式定义为节点分类的任务

目标是构建一个自监督辅助任务，该任务具有相应的损失${\mathcal{L}}_{self}$，可以与任务的损失${\mathcal{L}}_{task}$相结合去学习图神经网络，可以更好地概括无标签的数据

3 图上的基本辅助任务

3.1 结构信息

在图中提取自监督信息的第一个自然选择是数据背后的固有结构。因为图中数据是相关的，节点是被连接在一起。一个主要的方向是根据无标签节点的局部结构信息，或它们与图的其他部分的关系，为其构建自监督信息。换句话说，用于建立自监督的辅助任务的结构信息可以分类为本地或全局结构信息。

3.1.1 局部结构信息

局部结构自监督信息，它既可以来自于节点本身，也可以来自于该节点在其周围邻居中的结构关系。此外，辅助任务可以在单个节点上定义，也可以以配对/对比的方式开发，包括结合/比较多个节点的信息。

我们介绍了两个基于局部结构的SSL辅助任务的代表性例子

• NodeProperty（节点属性）

  在这项任务中，我们旨在预测图中每个节点的属性，如他们的度、局部节点重要性和局部聚类系数。这个辅助任务的目的是为了（进一步）鼓励GNN除了学习被优化的具体任务之外，还学习局部结构信息。构造自监督任务的损失

  $${\mathcal{L}}_{self}({\theta }^{\prime },A,X,{\mathcal{D}}_U)=\frac{1}{|{\mathcal{D}}_U|}\sum _{v_i\in {\mathcal{D}}_U}(f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?d_i{)}^2$$

  • $f_{{\theta }^{\prime }}$：预测节点度

• EdgeMask（边遮蔽）

  对于边缘掩码任务，我们寻求发展不仅基于单个节点本身的自我监督，而是基于图中两个节点之间的连接，成对地进行自我监督。我们首先随机屏蔽一些边，然后要求模型重建被屏蔽的边。然后，这里的 SSL 辅助任务是预测给定节点对之间是否存在链接。损失函数为：

  $${\mathcal{L}}_{self}({\theta }^{\prime },A,X,{\mathcal{D}}_U)=\frac{1}{|{\mathcal{M}}_e|}\sum _{(v_i,v_j)\in {\mathcal{M}}_e}l(f_w(|f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_j}|),1)+\frac{1}{|{\overline{\mathcal{M}}}_e|}\sum _{(v_i,v_j)\in {\overline{\mathcal{M}}}_e}l(f_w(|f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_j}|),1)$$

3.1.2 全局结构信息

给定节点的全局自监督信息不仅基于节点本身或仅限于其最近的局部ling’ju，而且还可以鸟瞰图中节点的位置。与局部视角类似，我们还提出了两个具有代表性的 SSL 借口任务，其中一个基于两个节点之间的全局成对比较，另一个来自单个节点如何在图中全局定位。

• PairwiseDistance

  辅助任务旨在能够区分/预测不同节点对之间的距离。距离的衡量方式有：是否在同一类中、个性化PageRank等计算节点相似度的链路预测方法。在本文中，选择使用最短路作为节点之间距离的衡量标准。首先计算所有节点对的最短路径长度将长度按1，2，3，其他分为四类。

  不选择更多类的原因：

  • 需要更多的计算来发现所有实际的节点对的最短路径长度
  • 较长的成对距离可能会过度拟合，使得变得有噪音
  • 计算所有节点需要的计算成本较高

  SSL损失被表述为多分类问题：

  $${\mathcal{L}}_{\text{self?}}\left({\theta }^{\prime },\mathbf{A},\mathbf{X},{\mathcal{D}}_U\right)=\frac{1}{|\mathcal{S}|}\sum _{\left(v_i,v_j\right)\in \mathcal{S}}?\left(f_w\left(\left|f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_j}\right|\right),C_{p_{ij}}\right)$$

  • $C_{p_{ij}}$：距离$p_{ij}$对应的分类

• Distance2Clusters：

  通过预测无标签的节点到预定的聚类的距离来探索全局结构信息。学习每个节点的全局位置向量。不需要节点计算到图中每个节点的距离，只需要计算到简历的聚类中心的距离即可。首先应用METI算法将图划分为k类。在每类中我们将高度节点作为聚类中心，记为$c_j$。使用向量$d_i$中第$j$个值记录节点$v_i$到第$j$类的聚类中心的距离。该任务的目标的优化问题可以表示为一个多元回归问题：

  $${\mathcal{L}}_{\text{self?}}\left({\theta }^{\prime },\mathbf{A},\mathbf{X},{\mathcal{D}}_U\right)=\frac{1}{\left|{\mathcal{D}}_U\right|}\sum _{v_i\in {\mathcal{D}}_U}{\Vert f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?{\mathbf{d}}_i\Vert }^2$$

3.2 属性信息

属性信息背后的关键点是帮助指导GNN，以确保节点/邻域属性信息的某些方面在自我监督的基于属性的辅助任务之后被编码在节点嵌入中。

• **AttributeMask：**与EdgeMask相似，随机的遮掩一些特征之后重建这些特征

  $${\mathcal{L}}_{\text{self?}}\left({\theta }^{\prime },\mathbf{A},\mathbf{X},{\mathcal{D}}_U\right)=\frac{1}{\left|{\mathcal{M}}_a\right|}\sum _{v_i\in {\mathcal{M}}_a}{\Vert f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?{\mathbf{x}}_i\Vert }^2$$

  由于现实中的数据集都是高维稀疏的，所以在应用AttributeMask之前，先使用PCA来获得降维的特征。

• PairwiseAttrSim： 建立基于属性的节点属性相似性的SSL辅助任务。由于大部分成对相似性接近于0，我们开发了一下采样策略。

  • 首先让${\mathcal{T}}_s$和${\mathcal{T}}_d$表示具有最高相似度和不相似度的节点对集合，定义为：

  T s = { ( v i , v j ) ∣ s i j ?in?top-K?of? { s i k } k = 1 N \ { s i i } , ? v i ∈ V U } T d = { ( v i , v j ) ∣ s i j ?in?bottom-K?of? { s i k } k = 1 N \ { s i i } , ? v i ∈ V U } \begin{aligned} \mathcal{T}_{s} &=\left\{\left(v_{i}, v_{j}\right) \mid s_{i j} \text { in top-K of }\left\{s_{i k}\right\}_{k=1}^{N} \backslash\left\{s_{i i}\right\}, \forall v_{i} \in \mathcal{V}_{U}\right\} \\ \mathcal{T}_{d} &=\left\{\left(v_{i}, v_{j}\right) \mid s_{i j} \text { in bottom-K of }\left\{s_{i k}\right\}_{k=1}^{N} \backslash\left\{s_{i i}\right\}, \forall v_{i} \in \mathcal{V}_{U}\right\} \end{aligned} Ts?Td??={(vi?,vj?)∣sij??in?top-K?of?{sik?}k=1N?\{sii?},?vi?∈VU?}={(vi?,vj?)∣sij??in?bottom-K?of?{sik?}k=1N?\{sii?},?vi?∈VU?}?

  • $s_{ij}$：度量两个节点之间的相似性，采用余弦相似度

  我们可以将回归问题形式化为：

  $${\mathcal{L}}_{\text{self?}}\left({\theta }^{\prime },\mathbf{A},\mathbf{X},{\mathcal{D}}_U\right)=\frac{1}{|\mathcal{T}|}\sum _{\left(v_i,v_j\right)\in \mathcal{T}}{\Vert f_w\left(\left|f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_i}?f_{{\theta }^{\prime }}(\mathcal{G}{)}_{v_j}\right|\right)?s_{ij}\Vert }^2$$

4 Preliminary Analysis

在本节中，我们提出了两种将这些辅助任务合并到GNN中的策略，即联合训练和两阶段训练，然后实证分析了辅助任务对GNN的影响。

4.1 联合训练

对图神经网络采用自我监督学习的一个自然思路是联合训练相应的损失。我们的目标是同时优化自监督损失${\mathcal{L}}_{self}$和监督损失${\mathcal{L}}_{task}$.

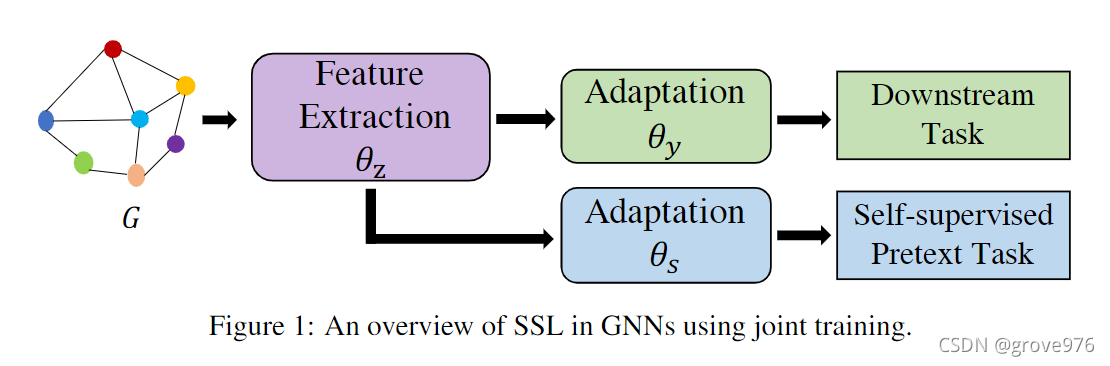
可以分为两个阶段：

• 特征提取过程：在输入图上进行特征提取，可以是多种图卷积层
  • $f_{{\theta }_z}(\mathcal{G})\to Z$表示特征提取器部分，其中$Z$是节点的嵌入，$z_i=f_{{\theta }_z}(\mathcal{G}{)}_{v_i}$
• 下游任务和自监督辅助任务的适应过程：可以是图卷积层或线性层
  • $f_{{\theta }_y}(z_i)\to {\hat{y}}_i$表示适配器部分，将节点$v_i$的嵌入$z_i$映射到预测的类别${\hat{y}}_i$

自监督的辅助任务可以被制定为相同的特征提取器$f_{{\theta }_z}$和一个额外的适配器$f_{{\theta }_s}$。因此整体目标可以定义为

$$\underset{\theta ,{\theta }^{\prime }}{\min }{\mathcal{L}}_{task}(\theta ,A,X,{\mathcal{D}}_L)+\lambda {\mathcal{L}}_{self}({\theta }^{\prime },A,X,{\mathcal{D}}_U)$$

4.2 两阶段训练

• 自监督辅助任务与训练
• 下游任务微调

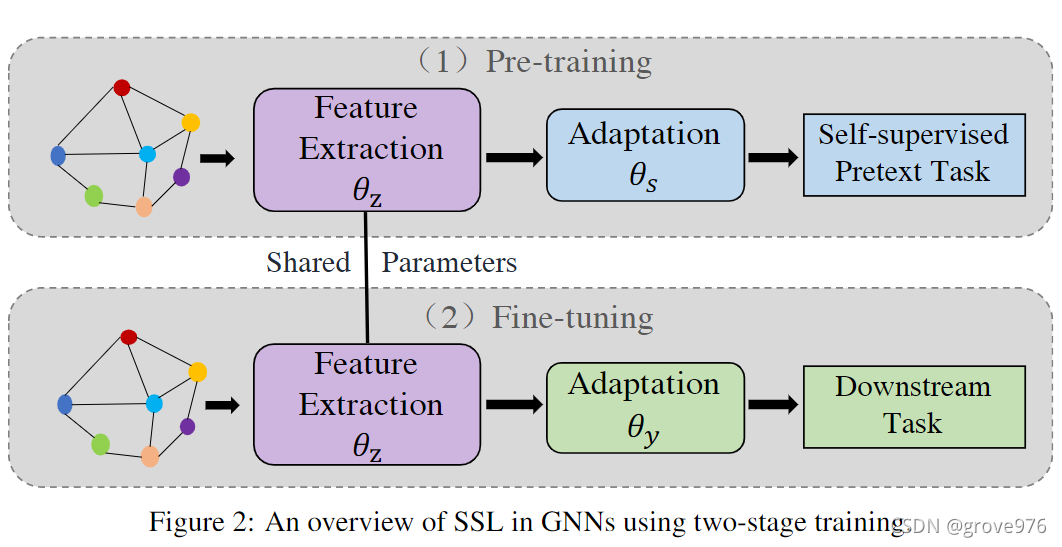
与联合训练类似，自监督模型由一个特征提取模块$f_{{\theta }_z}(\mathcal{G})$和一个自适应模块$f_{{\theta }_s}(\mathcal{G})$组成，这些模块的优化与下游任务无关。在自监督模型完全训练后，再开始训练下游任务模型。下游任务模型也有一个自适应模块$f_{{\theta }_y}(\mathcal{G})$，但它特征提取模块与自监督模块$f_{{\theta }_z}(\mathcal{G})$共享参数。如图所示，首先为辅助任务预训练自监督模型，然后使用自监督模型的特征提取模块作为下游任务的初始化。初始化后可以为下游任务固定它或者微调它。

4.3 实证研究

根据基本的辅助任务进行了广泛的实验，了解哪些SSL信息对GNN有效，哪些策略可以更好地为GNN集成SSL，并进一步分析SSL能够改善GNN的原因。

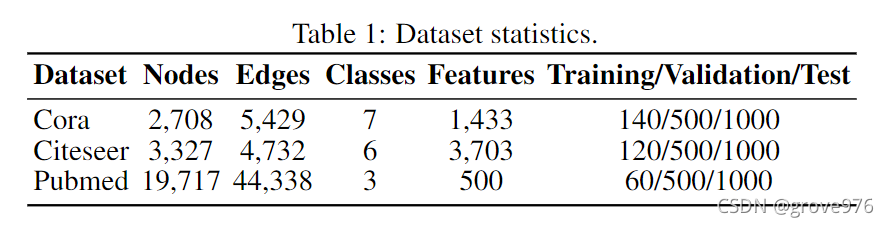
• Strategies for Two-stage Training

  对于两阶段训练，再初始化特征提取器后，我们可以对其进行固定或微调，以便进行节点分类。我们研究了预训练模型和节点分类模型的各种架构，结果如表所示。

  

  • “2GC+1Linear”：使用两层GCN进行特征提取，使用一层线性层进行自适应
  • “2GC”：一个用于特征提取的GCN和另一个用于自适应的GCN
  • 在 "Finetune Strategy "一栏中，"Fix "和 "Tune all "对应于上述两种策略，我们还报告了没有经过SSL预训练的节点分类性能，作为第三种策略
  • 所有的实验都是在PairwiseDistance任务下进行的，在大多数情况下，“Tune all”的策略实现了最佳性能

• SSL for GNNs

  • Joint Training vs. Two-stage Training

    我们观察到，虽然两阶段训练能够改进 vanilla GCN 模型，但联合训练在大多数情况下优于两阶段训练。因此，我们的实证分析表明，联合训练是将 SSL 与 GNN 集成的更好策略，而不是两阶段训练。

  • What SSL Works for GNNs

    从表 3 中，我们可以首先观察到，最好的性能总是由一个包含 SSL 借口任务的任务实现。我们的实证分析清楚地表明，在图神经网络中利用自我监督信息是一个很有前途的方向，可以进一步提高图结构数据的深度学习的性能。此外，我们观察到各种自监督的辅助任务在改善节点分类方面有广泛的效用。

    • 在所有数据集中，性能最好的方法是从全局结构信息开发的辅助任务
    • 我们确定AttributeMask的质量与GCN-PCA相比，因为它们都首先利用PCA作为预处理步骤来减少节点特征/属性的维度。
    • 我们发现 NodeProperty、EdgeMask 和 AttributeMask 的借口任务无法提升原始 GCN，因为性能差异始终小于 0.3%。相比之下，包括 PairwiseDistance、Distance2Cluster 和 PairwiseAttrSims 在内的全局自我监督成功地提高了性能

    

  • Why SSL Works for GNNs

    我们发现使用像全局结构的一些自我监督成对的成对属性信息可以很好地表现良好。正如我们之前提到的，用于节点分类的GCN是自然的半监督的，它已经探索了未标记的节点。

    如果GCN可以学习一种自监督，GCN的节点表示应该保留这样的信息，因此，它们在相应的借口任务上比原始节点功能更好地表达。性能差异如图3所示。

    

    选择三个有代表性的借口任务EdgeMask、NodeProperty 和PairwiseDistance 来说明，因为在其他情况下可以观察到类似的模式。EdgeMaskon Pubmed 的性能差异很小的原因可能是 Pubmed 的原始特征对局部连接非常具有代表性，因为原始特征在 EdgeMask 任务上可以达到 80% 以上的准确率。相反，在三个数据集中，PariwiseDisancetask的性能差异相当小。