从零开始 OpenCV 学习课-5. 图像的几何变换
本系列面向 Python 小白,从零开始实战解说 OpenCV 项目实战。
几何变换是指对图像的位置、大小、形状、投影进行变换,是将图像从原始平面投影到新的视平面。OpenCV 中的图像以多维数组描述,几何变换本质上是将一个多维数组通过映射关系求得另一个多维数组。
本节介绍图像的几何变换,提供完整例程和运行结果:位置变换:平移,旋转,镜像;形状变换:缩放,扭变;投影变换:透视投影,平行投影;极坐标变换。
1. 几何变换简介
几何变换是指对对图像的位置、大小、形状、投影进行变换,是将图像从原始平面投影到新的视平面。OpenCV 中的图像以多维数组描述,几何变换本质上是将一个多维数组通过映射关系求得另一个多维数组。
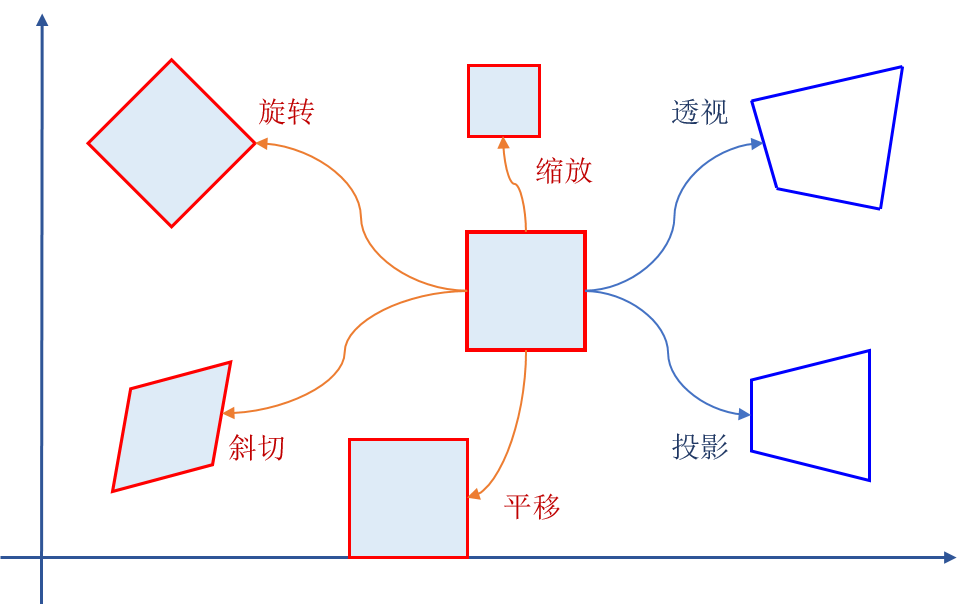
几何变换可以分为等距变换、相似变换、仿射变换和投影变换。在很多书籍中把等距变换、相似变换都称为仿射变换,常见的仿射变换包括平移、旋转、缩放、翻转、斜切等方法。
- 等距变换:图像中的长度、面积不变,典型的等距变换是 平移、旋转。
- 相似变换:图像中的长度比、夹角、虚圆点不变,相似变换是在等距变换的基础上进行了缩放,典型的相似变换是 缩放。
- 仿射变换:图像中的平行关系、面积比、共线线段或平行线段的长度比、矢量的线性组合不变,仿射变换是旋转和非均匀缩放的复合,典型的仿射变换是 斜切。
- 投影变换:图像中的共点、共线、相交、相切、拐点的关系不变,,投影变换是在仿射变换基础上进行的非线性缩放,典型的投影变换是 透视。
1.1 仿射变换
仿射变换(affine)的特点是原始图像中的平行关系和线段长度比例关系保持不变。
OpenCV 中的图像以多维数组描述,通过仿射变换变换为另一个多维数组(转换图像)。
仿射变换中的校正图像在二维空间中完成,在几何上定义为一个线性变换接一个平移变换。
仿射变换由以下公式描述:
[
x
~
y
~
1
]
=
M
A
[
x
y
1
]
,
M
A
=
[
a
11
a
12
a
13
a
21
a
22
a
23
0
0
1
]
\begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_A \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ,\hspace{1em} M_A= \begin{bmatrix} a_{11} &a_{12} &a_{13}\\ a_{21} &a_{22} &a_{23}\\ 0 &0 &1 \end{bmatrix}
???x~y~?1????=MA????xy1????,MA?=???a11?a21?0?a12?a22?0?a13?a23?1????
OpenCV 提供了 cv2.warpAffine 函数实现仿射变换的操作。
仿射变换矩阵 MA 中有 6 个未知参数,cv2.getAffineTransform 根据图像中不共线的 3 个点在变换前后的对应位置坐标,构造 6元一次方程组即可求出仿射变换矩阵 MA。cv2.warpAffine 再用变换矩阵 MA 计算得到变换后的图像。
基本例程:1.33 图像的仿射变换
# 1.33 仿射变换: 平移、镜像、旋转 (cv2.warpAffine)
img = cv2.imread("../images/imgB2.jpg") # 读取彩色图像(BGR)
rows, cols, ch = img.shape
pts1 = np.float32([[50, 50], [200, 50], [50, 200]]) # 初始位置
pts2 = np.float32([[50, 100], [200, 50], [100, 250]]) # 终止位置
MA = cv2.getAffineTransform(pts1, pts2) # 计算 2x3 变换矩阵 MA
dst = cv2.warpAffine(img, MA, (cols, rows)) # 实现仿射变换
plt.figure(figsize=(9,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original")
plt.subplot(122), plt.imshow(cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)), plt.title("warpAffine")
plt.show()

1.2 投影变换
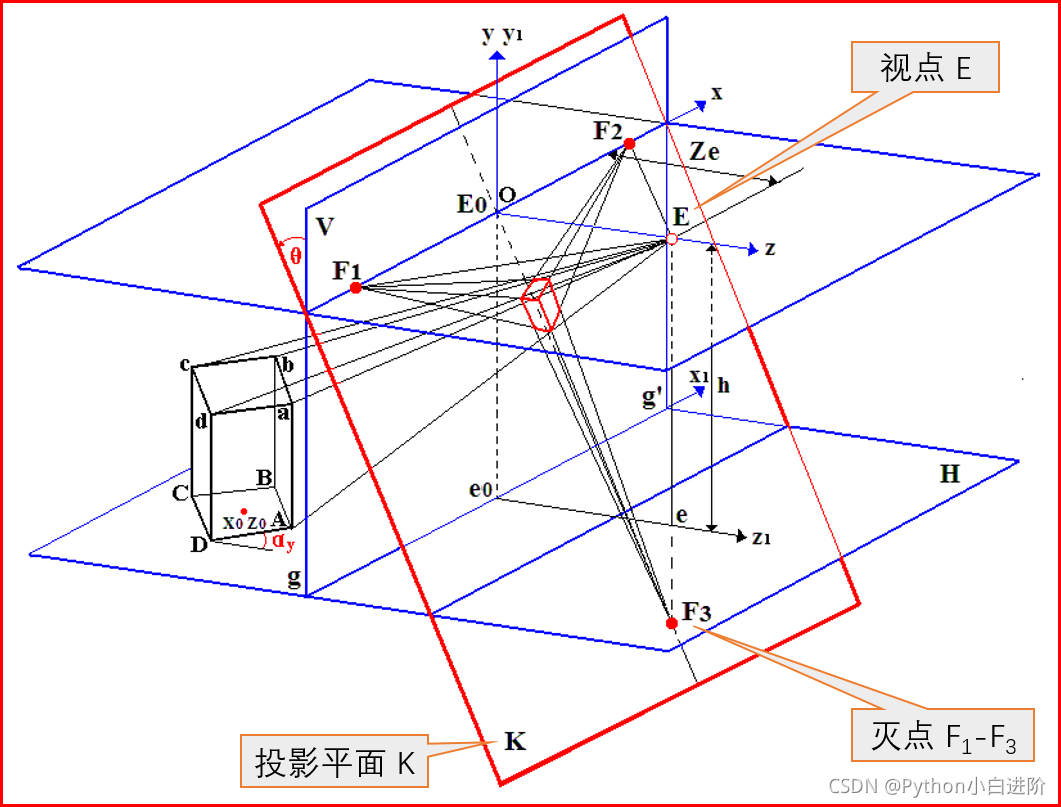
投影变换(Projective mapping)也称透视变换(Perspective transformation),其特点是:原始图像中的平行关系、比例关系在转换后可以改变,但直线在转换后仍然保持直线。
投影变换将图片投影到一个新的视平面(Viewing plane),可以对三维空间中的物体旋转进行校正,主要用于图像拼接和校正透视投影导致的图像失真 。
投影变换由以下公式描述:
[
x
~
y
~
z
~
]
=
M
[
x
y
z
]
,
M
=
[
a
11
a
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
]
\begin{bmatrix} \tilde{x}\\ \tilde{y}\\ \tilde{z} \end{bmatrix} = M \begin{bmatrix} x\\ y\\ z \end{bmatrix} ,\hspace{1em} M= \begin{bmatrix} a_{11} &a_{12} &a_{13}\\ a_{21} &a_{22} &a_{23}\\ a_{31} &a_{32} &a_{33} \end{bmatrix}
???x~y~?z~????=M???xyz????,M=???a11?a21?a31??a12?a22?a32??a13?a23?a33?????
OpenCV 提供了 cv2.warpPerspective 函数实现投影变换的操作。cv2.getPerspectiveTransform 根据图像中不共线的 4 个点在变换前后的对应位置求得 (3x3) 变换矩阵,cv2.warpPerspective 使用该 (3x3) 变换矩阵即可求出变换后的图像。
1.3 极坐标变换
极坐标变换可以校正图像中的圆形物体和圆环中所包含的物体。
极坐标变换由以下公式描述:
KaTeX parse error: No such environment: align* at position 8: \begin{?a?l?i?g?n?*?}? r &= \sqrt{(x-…
OpenCV 提供了 cv2.cartToPolar 函数和 cv2.ploarToCart 函数实现笛卡尔坐标与极坐标的相互转换。
2. 图像的平移
平移是物体位置在水平和垂直方向的移动。
像素点 (x,y) 沿 x 轴平移 dx、沿 y 轴平移 dy,可以由以下公式描述:
[
x
~
y
~
1
]
=
M
A
T
[
x
y
1
]
,
M
A
T
=
[
1
0
d
x
0
1
d
y
0
0
1
]
\begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_{AT} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ,\hspace{1em} M_{AT} = \begin{bmatrix} 1 &0 &d_x\\ 0 &1 &d_y\\ 0 &0 &1 \end{bmatrix}
???x~y~?1????=MAT????xy1????,MAT?=???100?010?dx?dy?1????
由偏移量 (Tx, Ty) 按上式构造平移变换矩阵 MAT,由函数 cv2.warpAffine 可以计算变换后的平移图像。
函数说明:
cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst
函数 cv2.warpAffine() 通过变换矩阵 M 对图像 src 进行仿射变换。
参数说明:
- scr:变换操作的输入图像
- M:仿射变换矩阵,2行3列
- dsize: 输出图像的大小,二元元组 (width, height)
- dst:变换操作的输出图像,可选项
- flags:插值方法,整型(int),可选项
- cv2.INTER_LINEAR:线性插值,默认选项
- cv2.INTER_NEAREST:最近邻插值
- cv2.INTER_AREA:区域插值
- cv2.INTER_CUBIC:三次样条插值
- cv2.INTER_LANCZOS4:Lanczos 插值
- borderMode:边界像素方法,整型(int),可选项,默认值为 cv2.BORDER_REFLECT
- borderValue:边界填充值,可选项,默认值为 0(黑色填充)
- 返回值:dst,变换操作的输出图像,ndarray 多维数组
注意事项:
- 变换前后的图像 src、dst 都是 ndarray 二维数组。
- 变换矩阵 M 反映平移或旋转的关系,是 np.float32 类型 ndarray 二维数组(2行*3列)。
- 平移变换矩阵 M = [(1,0,dx), (0,1,dy)],Tx 表示向右(负值向左)移动像素点数,Ty 表示向下(负值向上)移动像素点数。
- 输出图像的大小 dsize 的格式为元组 (width,height)。
基本例程:1.34 图像的平移
# 1.34 图像平移 (Translation transform)
img = cv2.imread("../images/imgLena.tif") # 读取彩色图像(BGR)
rows, cols, ch = img.shape
dx, dy = 100, 50 # dx=100 向右偏移量, dy=50 向下偏移量
MAT = np.float32([[1, 0, dx], [0, 1, dy]]) # 构造平移变换矩阵
# dst = cv2.warpAffine(img, MAT, (cols, rows)) # 默认为黑色填充
dst = cv2.warpAffine(img, MAT, (cols, rows), borderValue=(255,255,255)) # 设置白色填充
plt.figure(figsize=(9,6))
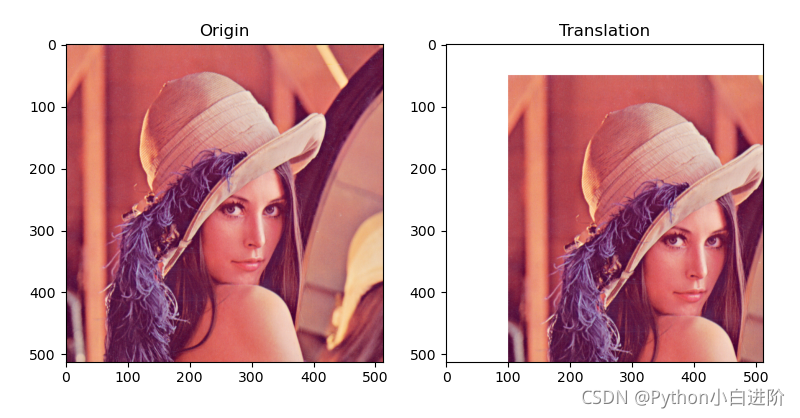
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original")
plt.subplot(122), plt.imshow(cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)), plt.title("Translational")
plt.show()
3. 图像的旋转
- 图像以原点 (0, 0) 为中心、顺时针旋转角度 θ 进行旋转操作,可以由以下公式描述:
[ x ~ y ~ 1 ] = M A R [ x y 1 ] , M A R = [ c o s θ ? s i n θ 0 s i n θ c o s θ 0 0 0 1 ] \begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_{AR} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} , M_{AR} = \begin{bmatrix} cos \theta &-sin \theta &0\\ sin \theta &cos \theta &0\\ 0 &0 &1 \end{bmatrix} ???x~y~?1????=MAR????xy1????,MAR?=???cosθsinθ0??sinθcosθ0?001????
按上式构造旋转变换矩阵 MAR,由函数 cv2.warpAffine 可以计算变换后的绕原点旋转图像。
- 图像以任意点 (x0, y0) 为旋转中心、顺时针旋转角度 θ 的旋转操作,可以先将原点平移到旋转中心 (x0, y0) ,然后按照原点旋转,最后再平移回坐标原点,可以由以下公式描述:
[ x ~ y ~ 1 ] = [ 1 0 x 0 0 1 y 0 0 0 1 ] [ c o s θ ? s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ 1 0 ? x 0 0 1 ? y 0 0 0 1 ] [ x y 1 ] \begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix}= \begin{bmatrix} 1 &0 &x_0\\ 0 &1 &y_0\\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} cos \theta &-sin \theta &0\\ sin \theta &cos \theta &0\\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &0 &-x_0\\ 0 &1 &-y_0\\ 0 &0 &1 \end{bmatrix} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ???x~y~?1????=???100?010?x0?y0?1???????cosθsinθ0??sinθcosθ0?001???????100?010??x0??y0?1???????xy1????
- 简便地,OpenCV 提供了 cv2.getRotationMatrix2D 函数, 根据旋转角度和位移计算旋转变换矩阵 MAR。
函数说明:
cv2.getRotationMatrix2D(center, angle, scale) → M
函数 getRotationMatrix2D 根据旋转参数计算旋转变换矩阵 MAR。
参数说明:
- center:旋转中心坐标,二元元组 (x0, y0)
- angle:旋转角度,单位为角度,逆时针为正数,顺时针为负数
- scale: 缩放因子
- 返回值:M, 旋转变换矩阵,2行3列
注意事项:
- 求出旋转变换矩阵 MAR,由函数 cv2.warpAffine 可以实现任意角度和任意中心的旋转效果。
- 以图像中心作为旋转中心时,可以用 img.shape 获得图像的宽度和高度值,除以 2 就是图像中心点坐标。
- 旋转角度为 90,180,270 度时,可以用 cv2.rotate(src, rotateCode) 函数实现,该方法实际上是通过矩阵转置实现的,因此速度很快。
基本例程:1.35 图像的旋转(以原点为中心旋转)
# 1.35 图像旋转 (以原点 (0,0) 为中心旋转)
img = cv2.imread("../images/imgLena.tif") # 读取彩色图像(BGR)
rows, cols, ch = img.shape
theta = np.pi / 8.0 # 顺时针旋转角度
cosTheta = np.cos(theta)
sinTheta = np.sin(theta)
MAT = np.float32([[cosTheta, -sinTheta, 0], [sinTheta, cosTheta, 0]]) # 构造旋转变换矩阵
# dst = cv2.warpAffine(img, MAT, (cols, rows)) # 默认为黑色填充
dst = cv2.warpAffine(img, MAT, (cols, rows), borderValue=(255,255,255)) # 设置白色填充
plt.figure(figsize=(9,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Origin")
plt.subplot(122), plt.imshow(cv2.cvtColor(dst, cv2.COLOR_BGR2RGB)), plt.title("Rotation")
plt.show()

基本例程:1.36 图像的旋转(任意旋转中心)
# 1.36 图像旋转 (以任意点 (x0,y0) 为中心旋转)
img = cv2.imread("../images/imgGaia.tif") # 读取彩色图像(BGR)
height, width = img.shape[:2] # 图片的高度和宽度
theta1, theta2 = 30, 45 # 顺时针旋转角度,单位为角度
x0, y0 = width//2, height//2 # 以图像中心作为旋转中心
MAR1 = cv2.getRotationMatrix2D((x0,y0), theta1, 1.0)
MAR2 = cv2.getRotationMatrix2D((x0,y0), theta2, 1.0)
imgR1 = cv2.warpAffine(img, MAR1, (width, height)) # 旋转变换,默认为黑色填充
imgR2 = cv2.warpAffine(img, MAR2, (width, height), borderValue=(255,255,255)) # 设置白色填充
plt.figure(figsize=(10,6))
plt.subplot(131), plt.axis('off'), plt.title(r"$Origin$")
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))
plt.subplot(132), plt.axis('off'), plt.title(r"$Rotation {}^o$".format(theta1))
plt.imshow(cv2.cvtColor(imgR1, cv2.COLOR_BGR2RGB))
plt.subplot(133), plt.axis('off'), plt.title(r"$Rotation {}^o$".format(theta2))
plt.imshow(cv2.cvtColor(imgR2, cv2.COLOR_BGR2RGB))
plt.show()

扩展例程:1.37 图像的直角旋转
当旋转角度为 90,180,270 度时,可以用图像旋转函数 cv2.rotate(src, rotateCode) 实现,该方法通过矩阵转置实现,速度很快。此外,numpy 中也提供了旋转矩阵的方法 np.rot90 可以按 90 度的整数倍进行旋转。
# 1.37 图像的直角旋转 (90, 180, 270)
# cv2.rotate(src, rotateCode)
# rotateCode: cv2.ROTATE_90_CLOCKWISE, 顺时针旋转90度
# cv2.ROTATE_180, 顺时针旋转180度
# cv2.ROTATE_90_COUNTERCLOCKWISE, 顺时针旋转270度
img = cv2.imread("../images/imgLena.tif") # 读取彩色图像(BGR)
imgR90 = cv2.rotate(img, cv2.ROTATE_90_CLOCKWISE)
imgR180 = cv2.rotate(img, cv2.ROTATE_180)
imgR270 = cv2.rotate(img, cv2.ROTATE_90_COUNTERCLOCKWISE)
# imgR90 = np.rot90(img, 1) # numpy 矩阵旋转 90*1=90 度
# imgR180 = np.rot90(img, 2) # numpy 矩阵旋转 90*2=180 度
# imgR270 = np.rot90(img, 3) # numpy 矩阵旋转 90*3=270 度
plt.figure(figsize=(9,7))
plt.subplot(221), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title(r"$Origin$")
plt.subplot(222), plt.imshow(cv2.cvtColor(imgR90, cv2.COLOR_BGR2RGB)), plt.title(r"$Rotation 90^{o}$")
plt.subplot(223), plt.imshow(cv2.cvtColor(imgR180, cv2.COLOR_BGR2RGB)), plt.title(r"$Rotation 180^{o}$")
plt.subplot(224), plt.imshow(cv2.cvtColor(imgR270, cv2.COLOR_BGR2RGB)), plt.title(r"$Rotation 270^{o}$")
plt.show()

4. 图像的翻转(镜像)
翻转也称镜像,是指将图像沿轴线进行轴对称变换。水平镜像是将图像沿垂直中轴线进行左右翻转,垂直镜像是将图像沿水平中轴线进行上下翻转,水平垂直镜像是水平镜像和垂直镜像的叠加。
以水平镜像为例,图像宽度为 fw,像素点 (x,y) 以垂直中轴线为中心进行左右对换,可以由以下公式描述:
[
x
~
y
~
1
]
=
M
A
F
[
x
y
1
]
,
M
A
F
=
[
?
1
0
f
w
0
1
0
0
0
1
]
\begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_{AF} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ,\hspace{1em} M_{AF} = \begin{bmatrix} -1 &0 &f_w\\ 0 &1 &0\\ 0 &0 &1 \end{bmatrix}
???x~y~?1????=MAF????xy1????,MAF?=????100?010?fw?01????
由上式构造镜像变换矩阵 MAF,由函数 cv2.warpAffine 可以计算变换后的镜像图像。
简便地,OpenCV 提供了 cv2.flip 函数,可以将图像沿水平方向、垂直方向、或水平/垂直方向同时进行翻转。
函数说明:
cv2.flip(src, flipCode[, dst]) -> dst
参数说明:
- scr:变换操作的输入图像
- flipCode:控制参数,整型(int),flipCode>0 水平翻转,flipCode=0 垂直翻转,flipCode<0 水平和垂直翻转
- dst:变换操作的输出图像,可选项
基本例程:1.38 图像的翻转(镜像)
# 1.38 图像的翻转 (镜像)
img = cv2.imread("../images/Fractal03.png") # 读取彩色图像(BGR)
imgFlip1 = cv2.flip(img, 0) # 垂直翻转
imgFlip2 = cv2.flip(img, 1) # 水平翻转
imgFlip3 = cv2.flip(img, -1) # 水平和垂直翻转
plt.figure(figsize=(9, 6))
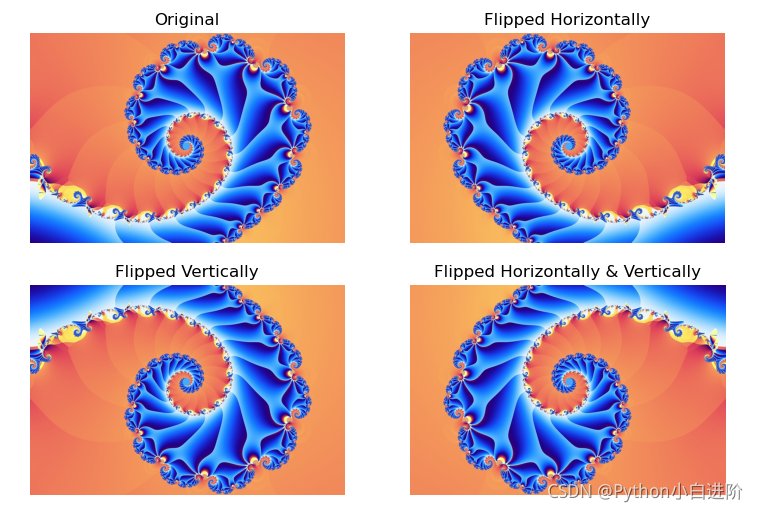
plt.subplot(221), plt.axis('off'), plt.title("Original")
plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)) # 原始图像
plt.subplot(222), plt.axis('off'), plt.title("Flipped Horizontally")
plt.imshow(cv2.cvtColor(imgFlip2, cv2.COLOR_BGR2RGB)) # 水平翻转
plt.subplot(223), plt.axis('off'), plt.title("Flipped Vertically")
plt.imshow(cv2.cvtColor(imgFlip1, cv2.COLOR_BGR2RGB)) # 垂直翻转
plt.subplot(224), plt.axis('off'), plt.title("Flipped Horizontally & Vertically")
plt.imshow(cv2.cvtColor(imgFlip3, cv2.COLOR_BGR2RGB)) # 水平垂直翻转
plt.show()
5. 图像的缩放
缩放只是调整图像的大小。
OpenCV 提供了 cv2.resize 函数,实现图像的缩放和大小变换 。
函数说明:
cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) → dst
参数说明:
- scr:变换操作的输入图像
- dsize: 输出图像的大小,二元元组 (width, height)
- dst:变换操作的输出图像,可选项
- fx, fy:x 轴、y 轴上的缩放比例,实型,可选项
- interpolation:插值方法,整型,可选项
- cv2.INTER_LINEAR:双线性插值(默认方法)
- cv2.INTER_AREA:使用像素区域关系重采样,缩小图像时可以避免波纹出现
- cv2.INTER_NEAREST:最近邻插值
- cv2.INTER_CUBIC:4x4 像素邻域的双三次插值
- cv2.INTER_LANCZOS4:8x8 像素邻域的Lanczos插值
- 返回值:dst,变换操作的输出图像,ndarray 多维数组
注意事项:
-
图像缩放可以通过 dsize 直接设定输出图像的大小,也可以通过 dx, dy 设置图像缩放的比例(dsize 设为 None)。
-
也可以通过构造缩放变换矩阵 MAZ,由函数 cv2.warpAffine 计算变换后的缩放平移图像。缩放变换矩阵 MAZ 由以下公式描述:
[ x ~ y ~ 1 ] = M A Z [ x y 1 ] , M A Z = [ f x 0 0 0 f y 0 0 0 1 ] \begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_{AZ} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ,\hspace{1em} M_{AZ} = \begin{bmatrix} f_x &0 &0\\ 0 &f_y &0\\ 0 &0 &1 \end{bmatrix} ???x~y~?1????=MAZ????xy1????,MAZ?=???fx?00?0fy?0?001????
由偏移量 (Tx, Ty) 按上式构造平移变换矩阵 MAT,由函数 cv2.warpAffine 可以计算变换后的平移图像。
基本例程:1.39 图像的缩放变换
# 1.39 图像的缩放
img = cv2.imread("../images/Fractal08.png") # 读取彩色图像(BGR)
height, width = img.shape[:2] # 图片的高度和宽度
imgZoom1 = cv2.resize(img, (int(0.75*width), int(height)))
imgZoom2 = cv2.resize(img, None, fx=0.75, fy=1.0, interpolation=cv2.INTER_AREA)
plt.figure(figsize=(8,6))
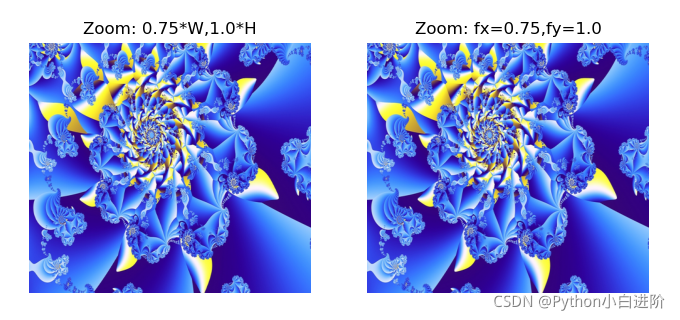
plt.subplot(121), plt.axis('off'), plt.title("Zoom: 0.75*W,1.0*H")
plt.imshow(cv2.cvtColor(imgZoom1, cv2.COLOR_BGR2RGB))
plt.subplot(122), plt.axis('off'), plt.title("Zoom: fx=0.75,fy=1.0")
plt.imshow(cv2.cvtColor(imgZoom2, cv2.COLOR_BGR2RGB))
plt.show()
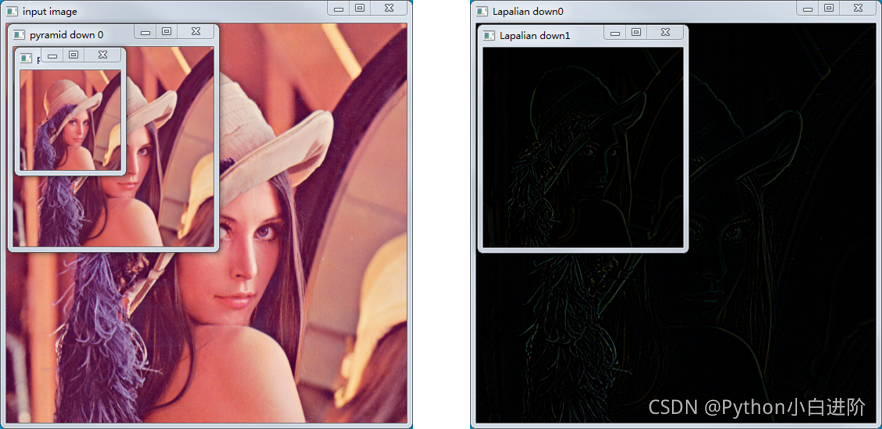
扩展例程:1.40 图像金字塔
图像金字塔是一种以多分辨率来解释图像的结构,常用于图像分割、图像压缩和机器视觉。
在需要处理同一图像的不同分辨率的子图时,需要创建一组具有不同分辨率的原始图像。把最大的图像放在底部,最小的放在顶部,看起来就像一座金字塔,称为图像金字塔。
图像金字塔是一系列来源于同一张原始图像、以金字塔形状排列的分辨率逐步降低的图像集合。
金字塔的底部是原始图像的高分辨率的表示,顶部是低分辨率的近似。
OpenCV 为向下采样和向上采样提供了两个函数:cv2.pyrDown 和 cv2.pyrUp。
函数说明:
cv2.pyrDown(src, dst=None, dstsize=None, borderType=None) → dst # 向下采样
cv2.pyrUp(src, dst=None, dstsize=None, borderType=None) → dst # 向上采样
函数 cv2.pyrDown 是从高分辨率的大尺寸图像逐次向下采样得到一系列图像,构建一个金字塔,称为高斯金字塔(Gaussian pyramid),实际上是一个重复高斯平滑并重新对图像采样的过程。拉普拉斯金字塔每次向下采样后将再次向上采样,并记录残差信息,可以对图像进行最大程度的还原。
# 1.40 图像金字塔
def GussianPyramid(image): # 高斯金字塔
level = 2 # 金字塔的层数
imgCopy = image.copy()
pyramidImages = [] # 创建图像 List
for i in range(level):
dst = cv2.pyrDown(imgCopy) # 下采样
pyramidImages.append(dst) # 添加到图像 List
cv2.imshow("pyramid down "+str(i), dst)
imgCopy = dst.copy()
return pyramidImages
img = cv2.imread("../images/imgLena.tif") # 读取彩色图像(BGR)
cv2.namedWindow("input image", cv2.WINDOW_AUTOSIZE)
cv2.imshow("input image", img)
GussianPyramid(img) # 高斯图像金字塔
# LapalianPyramid(img) # 拉普拉斯图像金字塔
cv2.waitKey(0)
6. 图像的扭变(错切)
图像的错切变换也称斜切,是指平面景物在投影平面上的非垂直投影,使图像中的图形在水平方向或垂直方向产生扭变。
以水平扭变为例,像素点 (x,y) 在水平方向发生扭变变成斜边,而在垂直方向的边不变,可以由以下公式描述:
[
x
~
y
~
1
]
=
M
A
S
[
x
y
1
]
,
M
A
S
=
[
1
t
a
n
θ
0
0
1
0
0
0
1
]
\begin{bmatrix} \tilde{x}\\ \tilde{y}\\ 1 \end{bmatrix} = M_{AS} \begin{bmatrix} x\\ y\\ 1 \end{bmatrix} ,\hspace{1em} M_{AS} = \begin{bmatrix} 1 &tan \theta &0\\ 0 &1 &0\\ 0 &0 &1 \end{bmatrix}
???x~y~?1????=MAS????xy1????,MAS?=???100?tanθ10?001????
由扭变角度 θ上式构造错切变换矩阵 MAS,由函数 cv2.warpAffine 可以计算变换后的扭变图像。
基本例程:1.41 图像的错切
# 1.41 图像的错切
img = cv2.imread("../images/imgB2.jpg") # 读取彩色图像(BGR)
height, width = img.shape[:2] # 图片的高度和宽度
MAS = np.float32([[1, 0.2, 0], [0, 1, 0]]) # 构造错切变换矩阵
imgShear = cv2.warpAffine(img, MAS, (width, height))
plt.figure(figsize=(9,6))
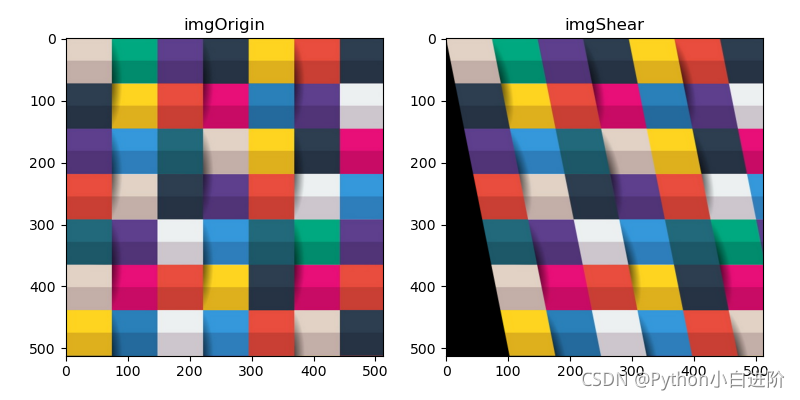
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("imgOrigin")
plt.subplot(122), plt.imshow(cv2.cvtColor(imgShear, cv2.COLOR_BGR2RGB)), plt.title("imgShear")
plt.show()
7. 图像的复合变换
图像的复合变换是指对给定的图像连续进行多次上述的平移、旋转、翻转、缩放、错切等基本变换,也称为级联变换。
对给定图像按一定顺序执行若干次基本变换,其变换矩阵仍然可以用 3x3 阶变换矩阵表示。进一步地,对图像依次执行基本变换 F1、F2、…Fn 的变换矩阵分别为 M1、M2、…Mn,可以证明,以图像中心点为中心进行比例、旋转进行变换,则复合变换的变换矩阵 M 等于各基本变换矩阵依次相乘所得到的组合矩阵:
M
=
M
1
×
M
2
×
?
×
M
n
M = M_1 \times M_2 \times \dots \times M_n
M=M1?×M2?×?×Mn?
缩放:
M
A
Z
=
[
f
x
0
0
0
f
y
0
0
0
1
]
M_{AZ} = \begin{bmatrix} fx &0 &0\\ 0 &f_y &0\\ 0 &0 &1 \end{bmatrix}
MAZ?=???fx00?0fy?0?001????
旋转:
M
A
R
=
[
c
o
s
θ
?
s
i
n
θ
0
s
i
n
θ
c
o
s
θ
0
0
0
1
]
M_{AR} = \begin{bmatrix} cos \theta &-sin \theta &0\\ sin \theta &cos \theta &0\\ 0 &0 &1 \end{bmatrix}
MAR?=???cosθsinθ0??sinθcosθ0?001????
平移:
M
A
T
=
[
1
0
d
x
0
1
d
y
0
0
1
]
M_{AT} = \begin{bmatrix} 1 &0 &d_x\\ 0 &1 &d_y\\ 0 &0 &1 \end{bmatrix}
MAT?=???100?010?dx?dy?1????
扭变:
M
A
S
=
[
1
t
a
n
θ
0
0
1
0
0
0
1
]
M_{AS} = \begin{bmatrix} 1 &tan \theta &0\\ 0 &1 &0\\ 0 &0 &1 \end{bmatrix}
MAS?=???100?tanθ10?001????
镜像:
M
A
F
=
[
?
1
0
f
w
0
1
0
0
0
1
]
M_{AF} = \begin{bmatrix} -1 &0 &f_w\\ 0 &1 &0\\ 0 &0 &1 \end{bmatrix}
MAF?=????100?010?fw?01????
基本例程:1.42 图像的复合变换
# 1.42 图像的复合变换
img = cv2.imread("../images/imgLena.tif") # 读取彩色图像(BGR)
height, width = img.shape[:2] # 图片的高度和宽度
# (1) 缩放
fx, fy = 0.6, 0.6
MAZ = np.float32([[fx, 0, 0], [0, fy, 0]]) # 构造缩放变换矩阵
imgT1 = cv2.warpAffine(img, MAZ, (width, height)) # 仿射变换, 黑色填充
# (2) 平移
dx, dy = 50, 200 # dx=100 向右偏移量, dy=50 向下偏移量
MAT = np.float32([[1, 0, dx], [0, 1, dy]]) # 构造平移变换矩阵
imgT2 = cv2.warpAffine(imgT1, MAT, (width, height), borderValue=(0,255,255)) # 实现仿射变换
# (3) 旋转
theta = -30 * np.pi / 180 # 逆时针旋转 30°
cosTheta = np.cos(theta)
sinTheta = np.sin(theta)
MAR = np.float32([[cosTheta, -sinTheta, 0], [sinTheta, cosTheta, 0]]) # 构造旋转变换矩阵
imgT3 = cv2.warpAffine(imgT2, MAR, (width, height), borderValue=(255,255,0)) # 实现仿射变换
# (4) 扭曲
theta = -30 * np.pi / 180 # 逆时针扭变 30°
MAS = np.float32([[1, np.tan(theta), 0], [0, 1, 0]]) # 构造扭变变换矩阵
imgT4 = cv2.warpAffine(imgT3, MAS, (width, height), borderValue=(255,0,255)) # 实现仿射变换
plt.figure(figsize=(9,6))
plt.subplot(221), plt.axis('off'), plt.title("T1:Zoom")
plt.imshow(cv2.cvtColor(imgT1, cv2.COLOR_BGR2RGB)),
plt.subplot(222), plt.axis('off'), plt.title("T2:Translation")
plt.imshow(cv2.cvtColor(imgT2, cv2.COLOR_BGR2RGB))
plt.subplot(223), plt.axis('off'), plt.title("T3:Rotation")
plt.imshow(cv2.cvtColor(imgT3, cv2.COLOR_BGR2RGB))
plt.subplot(224), plt.axis('off'), plt.title("T4:Shear")
plt.imshow(cv2.cvtColor(imgT4, cv2.COLOR_BGR2RGB))
plt.show()

8. 投影变换
投影变换(Projective mapping)也称透视变换(Perspective transformation)是建立两平面场之间的对应关系, 将图片投影到一个新的视平面(Viewing plane)。
OpenCV 提供了 cv2.warpPerspective 函数实现投影变换的操作。
函数说明:
cv2.getPerspectiveTransform(src, dst[,solveMethod]) → MP
cv2.warpPerspective(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst
函数cv2.getPerspectiveTransform 根据图像中不共线的 4 个点在变换前后的对应位置求得 (3x3) 变换矩阵,cv2.warpPerspective 使用该 (3x3) 变换矩阵即可求出变换后的图像。标量进行加法运算。
参数说明:
- src:变换前图像四边形顶点坐标
- dst:变换后图像四边形顶点坐标
- solveMethod:矩阵分解方法,传递给 cv2.solve 求解变换矩阵 MP
- cv2.DECOMP_LU:选择最优轴的高斯消去法,默认方法
- cv2.DECOMP_SVD:奇异值分解(SVD)方法
- cv2.DECOMP_EIG:特征值分解方法,src 必须对称
- cv2.DECOMP_QR:QR(正交三角)分解
- cv2.DECOMP_CHOLESKY:Cholesky LLT 分解
- MP:透视变换矩阵,3行3列
- dsize: 输出图像的大小,二元元组 (width, height)
- dst:变换操作的输出图像,可选项
- flags:插值方法,整型(int),可选项
- cv2.INTER_LINEAR:线性插值,默认选项
- cv2.INTER_NEAREST:最近邻插值
- cv2.INTER_AREA:区域插值
- cv2.INTER_CUBIC:三次样条插值
- cv2.INTER_LANCZOS4:Lanczos 插值
- borderMode:边界像素方法,整型(int),可选项,默认值为 cv2.BORDER_REFLECT
- borderValue:边界填充模式,可选项,默认值为 0(黑色填充)
- 返回值:dst,透视变换操作的输出图像,ndarray 多维数组
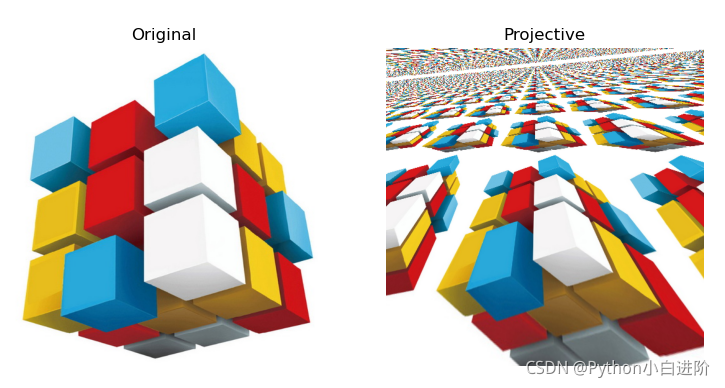
基本例程:1.43 图像的投影变换
# 1.43 投影变换 (Projective mapping)
img = cv2.imread("../images/imgB2.jpg") # 读取彩色图像(BGR)
h, w = img.shape[:2] # 图片的高度和宽度
pointSrc = np.float32([[0,0], [w-1,0], [0,h-100], [w-1, h-100]]) # 原始图像中 4点坐标
pointDst = np.float32([[180,50], [w-180,50], [0,h-100], [w-1, h-100]]) # 变换图像中 4点坐标
MP = cv2.getPerspectiveTransform(pointSrc, pointDst) # 计算投影变换矩阵 M
imgP = cv2.warpPerspective(img, MP, (512, 512)) # 用变换矩阵 M 进行投影变换
plt.figure(figsize=(9,6))
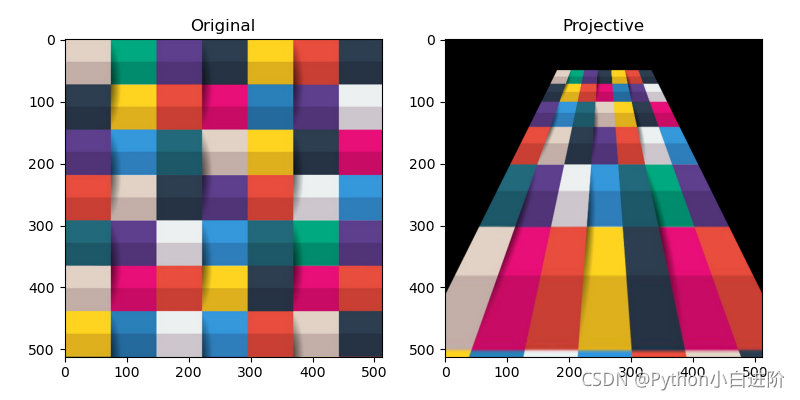
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original")
plt.subplot(122), plt.imshow(cv2.cvtColor(imgP, cv2.COLOR_BGR2RGB)), plt.title("Projective")
plt.show()
基本例程:1.44 图像的投影变换
# 1.44 图像的投影变换
img = cv2.imread("../images/imgC2.jpg") # 读取彩色图像(BGR)
h, w = img.shape[:2] # 图片的高度和宽度
pointSrc = np.float32([[0,0], [w,0], [0,h], [w,h]]) # 原始图像中 4点坐标
pointDst = np.float32([[int(w/3), int(h/3)], [int(w*2/3), int(h/3)], [0,h], [w,h]]) # 变换图像中 4点坐标
MP = cv2.getPerspectiveTransform(pointSrc, pointDst) # 计算投影变换矩阵 M
imgP = cv2.warpPerspective(img, MP, (w,h), flags=cv2.INTER_AREA, borderMode=cv2.BORDER_WRAP)
plt.figure(figsize=(9,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original"), plt.axis('off')
plt.subplot(122), plt.imshow(cv2.cvtColor(imgP, cv2.COLOR_BGR2RGB)), plt.title("Projective"), plt.axis('off')
plt.show()
9. 直角坐标与极坐标的转换
函数 cv2.cartToPolar 用于将直角坐标(笛卡尔坐标)转换为极坐标,函数 cv2.polarToCart 用于将极坐标转换为直角坐标(笛卡尔坐标)。
圆形图案边缘上的文字经过及坐标变换后可以垂直的排列在新图像的边缘,便于对文字的识别和检测。
函数说明:
cv2.cartToPolar(x, y[, magnitude[, angle[, angleInDegrees]]]) → magnitude, angle
cv2.polarToCart(magnitude, angle[, x[, y[, angleInDegrees]]]) → x, y
函数 cv2.cartToPolar 实现将原点移动到变换中心后的直角坐标向极坐标的转换,输入参数为直角坐标系的横坐标、纵坐标,输出为极坐标系的向量值、角度值。
函数 cv2.polarToCart 实现将原点移动到变换中心后的极坐标向直角坐标的转换,输入参数为极坐标系的向量值、角度值,输出为直角坐标系的横坐标、纵坐标。
参数说明:
- x, y:直角坐标系的横坐标、纵坐标,ndarray 多维数组,浮点型
- magnitude, angle:极坐标系的向量值、角度值,ndarray 多维数组
- angleInDegrees:弧度制/角度值选项,默认值 0 选择弧度制,1 选择角度制([0,360] )
- 返回值 magnitude, angle:极坐标系的向量值、角度值,ndarray 多维数组,与输入的 x, y 具有相同的尺寸和数据类型
- 返回值 x, y:直角坐标系的横坐标、纵坐标,ndarray 多维数组,与输入的 magnitude, angle 具有相同的尺寸和数据类型
注意事项:
- 极坐标与直角坐标的变换在数学上是可逆的,但实际变换时存在误差,角度计算精度约为 0.3度,坐标计算精度约为 1e-6。
- 直角坐标系以变换中心为圆心的同一个圆上的点,在极坐标系中显示为一条直线。因此,用极坐标变换可以实现圆形物体的图像修正。
- cv2.cartToPolar 中的可选项 magnitude, angle 可以用于指定变换中心的坐标,cv2.polarToCart 中的可选项 x, y 可以用于指定变换中心的坐标。
基本例程:1.45 直角坐标转换为极坐标
# 1.45 直角坐标转换为极坐标
x = np.float32([0,1,2, 0,1,2, 0,1,2]) -1
y = np.float32([0,0,0, 1,1,1, 2,2,2]) -1
n = np.arange(9)
r, theta = cv2.cartToPolar(x, y, angleInDegrees=True)
xr,yr = cv2.polarToCart(r, theta, angleInDegrees=1)
print(xr,yr)
plt.figure(figsize=(9,5))
plt.subplot(121), plt.title("Cartesian coordinate"), plt.plot(x, y, 'o')
for i, txt in enumerate(n):
plt.annotate(txt, (x[i], y[i]))
plt.subplot(122), plt.title("Polar coordinate"), plt.plot(r, theta, 'o')
for i, txt in enumerate(n):
plt.annotate(txt, (r[i], theta[i]))
plt.show()
扩展例程:1.46 极坐标系中的圆形图像修正
# 1.46 极坐标系中的圆形图像修正
img = cv2.imread("../images/imgC3.jpg") # 读取彩色图像(BGR)
h, w = img.shape[:2] # 图片的高度和宽度
cx, cy = int(w/2), int(h/2) # 以图像中心点作为变换中心
maxR = max(cx, cy) # 最大变换半径
imgPolar = cv2.linearPolar(img, (cx,cy), maxR, cv2.INTER_LINEAR)
imgPR = cv2.rotate(imgPolar, cv2.ROTATE_90_COUNTERCLOCKWISE)
plt.figure(figsize=(10,6))
plt.subplot(121), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("Original"), plt.axis('off')
plt.subplot(122), plt.imshow(cv2.cvtColor(imgPR, cv2.COLOR_BGR2RGB)), plt.title("PolarTrans"), plt.axis('off')
plt.show()
通过极坐标和直角坐标的对应关系,将圆环图像转换为矩形图像,可以对圆形图像进行修正。

【本节完】
版权声明:
欢迎关注『Python 小白从零开始 OpenCV 学习课 @ youcans』 原创作品
原创作品,转载必须标注原文链接:https://blog.csdn.net/youcans/article/details/121136047
Copyright 2021 youcans, XUPT
Crated:2021-11-14