提示:《改进后》是基于《改进前》的后续
经典功率谱估计
前言
在周期图法和BT法中,功率谱估计的原信号设为高斯白噪声,因为BT法必须用在广义平稳随机过程,所以现有的函数只有周期图法的函数,所以前半部分中,两种方法我都用单一样本表示,改进前的matlab程序全都是从原始公式开始写,这样可以更方便地了解两种方法的内部过程。最后也会给出功率谱估计的质量:偏差和方差。
而在改进方法中,我们直接用Pwelch函数来实现分段的周期图法;而由于没有直接的分段的BT法公式(可能是因为BT法只能用在广义平稳过程中,又或者BT法效果没有周期法好),所以在单一样本的基础上,先进行分段处理,每段再各自利用BT法处理,最后再求平均,来实现分段的BT法。第三个方法是利用MTM法来实现分辨率和方差的平衡。
一、功率谱估计方法(改进前)
1.周期图法
2.BT法
3.周期图法和BT法的关系
4.功率谱估计的质量
改进前的这些谱估计方法在上一节已描述,本节介绍改进方法。
二、功率谱估计的改进
分段方法主要分为两大类:Bartlett平均法和Welch平均法。Bartlett平均法是不重叠的分段法,而Welch平均法是重叠的分段法。
1.基于周期图法下的分段方法可以利用Pwelch函数来描述,
也有的程序会用psd函数,但我help了一下,显示如下,说明还是以pwelch函数为主吧!

2.基于BT法的分段方法没有可以直接调用的函数,本文结合BT法和两种分段法从基础公式来分析,也顺便了解一下非重叠分段和重叠分段的区别。
为了对比各个方法,以下程序的基础都建立在x有20000个点,
FFT个数为20000点,Fs=1; n=0:N-1,且公式为:
x=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));
1.Pwelch法(周期图法下的分段方法)
此方法是可以直接调用函数Pwelch,本文调用的是:
[pxx,f] = pwelch(x,window,noverlap,Nfft,Fs)
其中输入参数的涵义是:
-
x:被估计的信号
-
window:为了使功率谱变得平滑而加的窗函数,默认hamming窗
窗函数查询 -
noverlap:表示两段之间的重叠个数
-
Nfft:表示fft的点数,Nfft> X,默认值为256点
-
Fs:表示采样频率,实际频率f(Hz)/Fs=归一化频率w(rad/s)/2pi
输出参数:
- pxx:功率谱
- f:横坐标,范围[0 pi*Fs]
若想查看其他形式,help一下即可。
如果使用boxcar窗,并且NOVERLAP=0,则可得到Bartlett法的平均周期图。
%% 周期图法的分段方法
clc;close all;clear;
N=20000; Nfft=20000; Fs=1; n=0:N-1;
x=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));
M=256; %%注意M的取值,过小时会导致分别率过小
%% Bartlett平均法
window1=boxcar(M); noverlap1=0;
figure;
subplot(2,1,1);
[Pxx1,f]=pwelch(x,window1,noverlap1,Nfft);
plot(f/pi,Pxx1);grid on;title('基于周期图法的Bartlett平均法');
%为了方便看出线谱位置(pi前面的系数),将f除以pi。
%如果使用boxcar窗,且NOVERLAP=0,则可得到Bartlett法的平均周期图
%% Welch平均
window2=hamming(M); noverlap2=M/2;
[Pxx2,f]=pwelch(x,window2,noverlap2,Nfft);
subplot(2,1,2);
plot(f/pi,Pxx2);grid on;title('基于周期图法的Bartlett平均法');
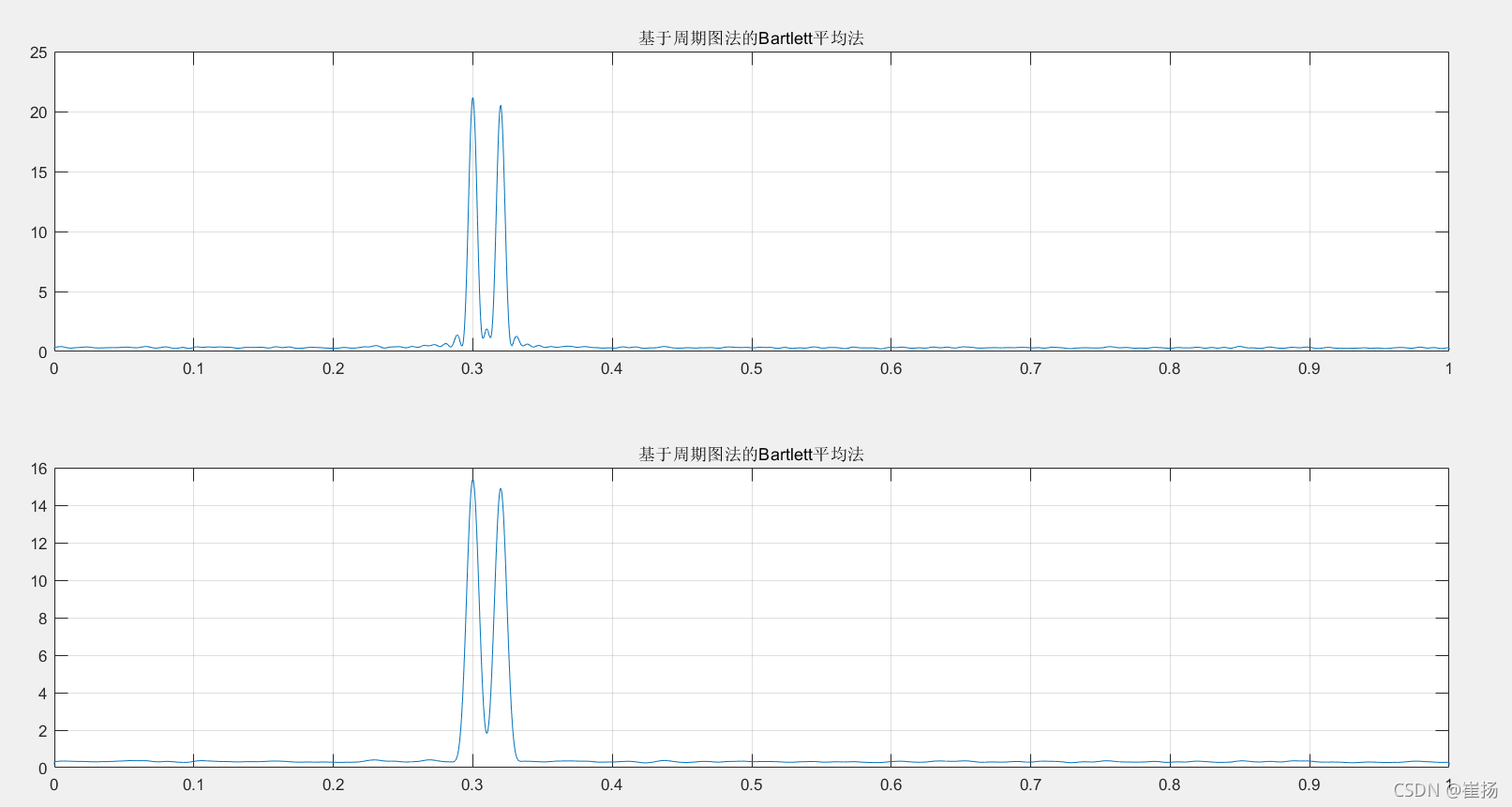
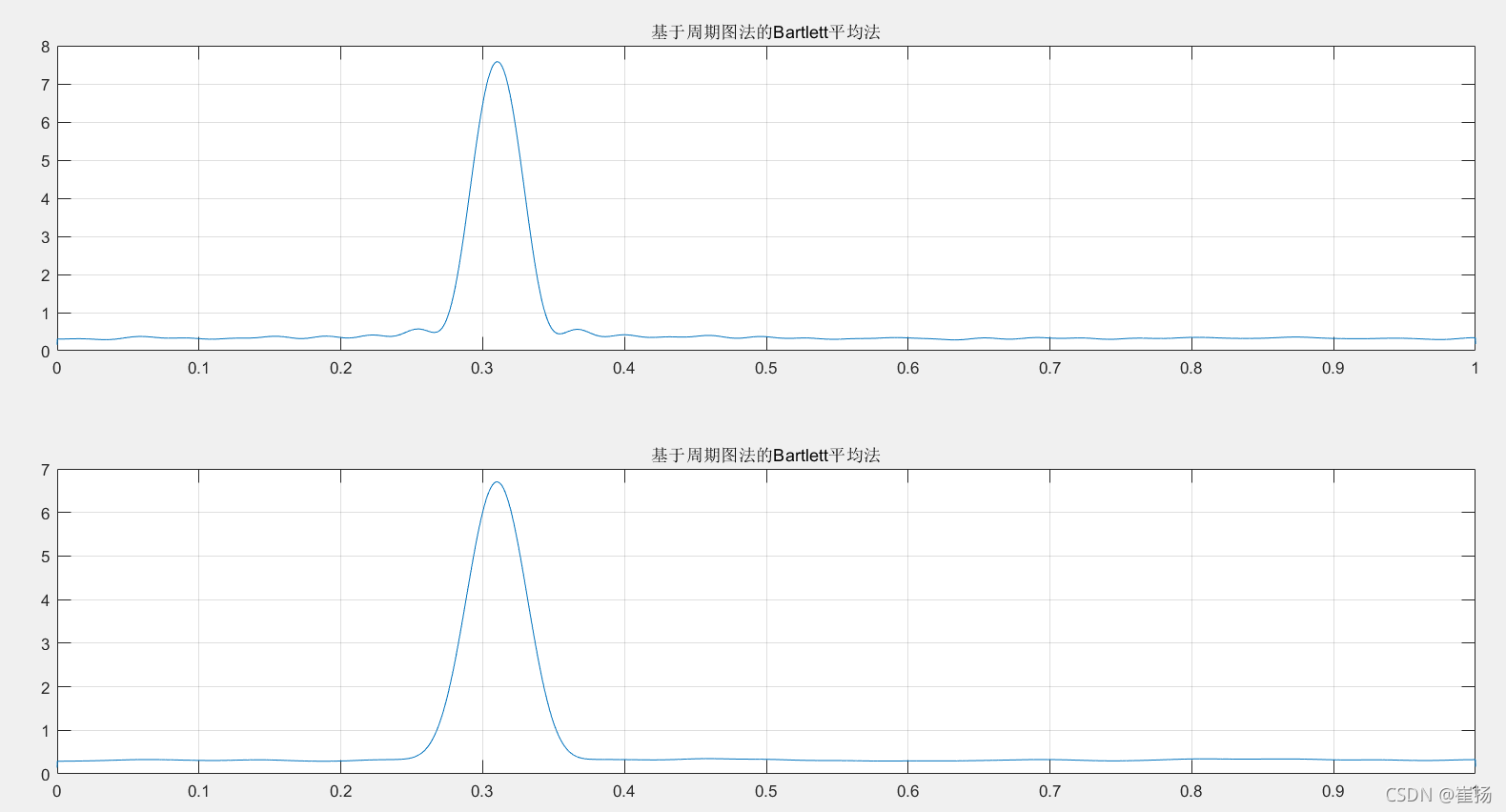
这里值得注意的是:不能将窗函数的点数设太小,否则可能导致分辨率过小导致分辨不出这两个频率。当M=64,结果如下:
2.BT法下的分段方法
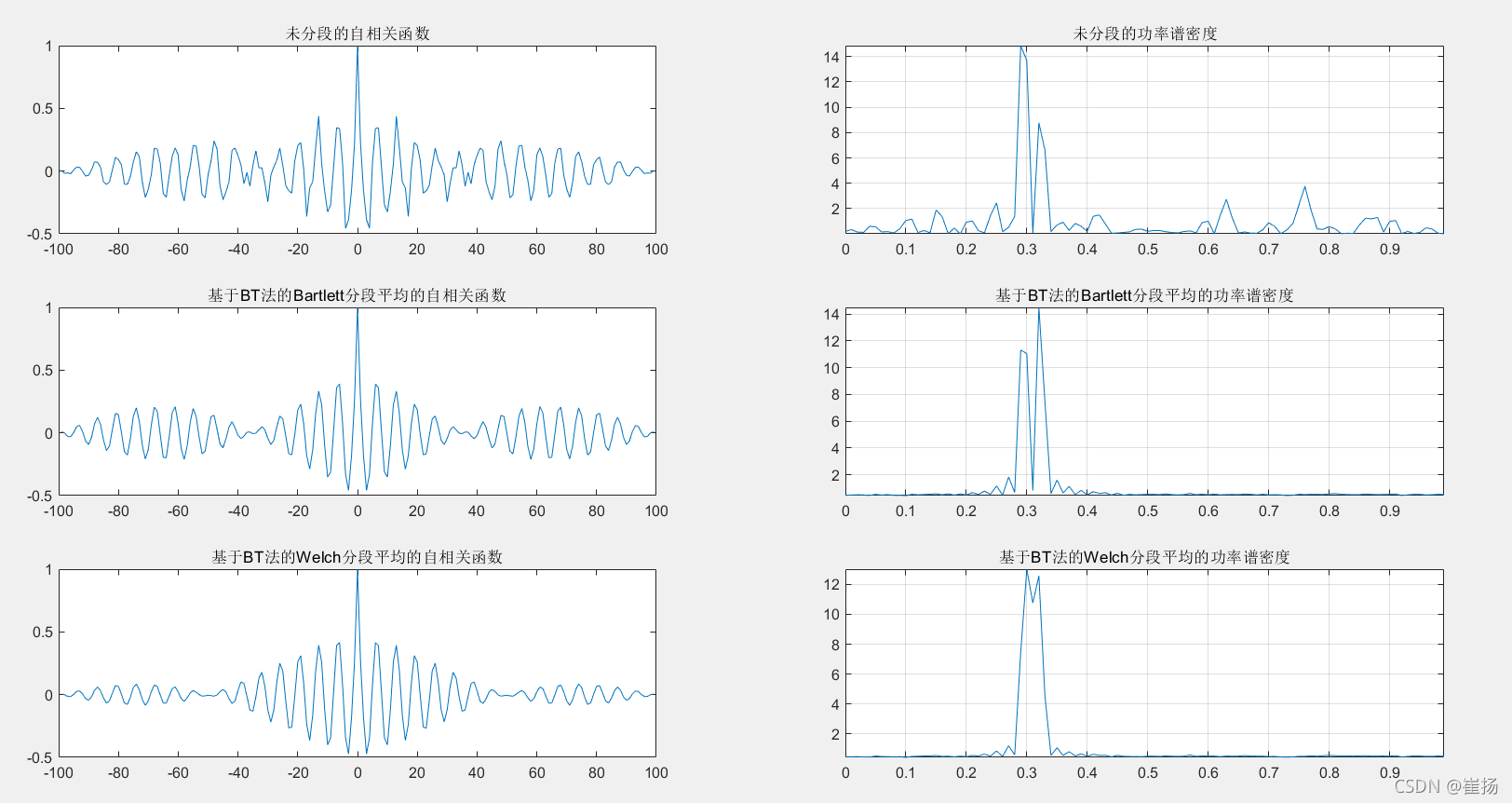
由于没有基于BT法的分段函数,以下是人为将其分段,再将结果做平均。为了做一组对照实验,还加入了一组不分段的数(但是这个数用的是分段后的其中一段,其实在点数是不公平的,分辨率会不如点数多的情况,但点数多了方差又会很大)。
%% BT法的分段方法
clc;clear all;close all;
N=20000; %%当分段数不多时,可能分辨率不够,将增大N点即可
K=200; %%分段数目
M=N/K; %%每段的采样点数
n=1:N;
x1=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));
for k=1:K
x(k,:)=x1(M*k-M+1:M*k);
end
%% Bartlett平均法
for i=1:K
[rx_BT(i,:),lags]=xcorr(x(i,:),'coeff');
sf_BT(i,:)=fftshift(abs(fft(rx_BT(i,:))));
end
rx_BT_AV=sum(rx_BT)/K;
sf_BT_AV=sum(sf_BT)/K;
lags1=lags/M; %%使横轴为单位为[0 0.5]
figure;
subplot(3,2,1);
plot(lags,rx_BT(1,:));title('未分段的自相关函数');
subplot(3,2,2);
plot(lags1,sf_BT(1,:));title('未分段的功率谱密度');grid on;
axis([0 +inf -inf +inf]);
subplot(3,2,3);
plot(lags,rx_BT_AV);title('基于BT法的Bartlett分段平均的自相关函数');
subplot(3,2,4);
plot(lags1,sf_BT_AV);title('基于BT法的Bartlett分段平均的功率谱密度');grid on;
axis([0 +inf -inf +inf]);
%% Welch平均
for i=1:1:K-1
[rx_BT1(2*i-1,:),lags]=xcorr(x(i,:),'coeff');
[rx_BT1(2*i,:),lags]=xcorr([x(i,M/2+1:M),x(i+1,1:M/2)],'coeff');
end
[rx_BT1(2*K-1,:),lags]=xcorr(x(K,:),'coeff');
[rx_BT1(2*K,:),lags]=xcorr([x(K,M/2+1:M),x(1,1:M/2)],'coeff');
for i=1:2*K
sf_BT1(i,:)=fftshift(abs(fft(rx_BT1(i,:))));
end
rx_BT1_AV=sum(rx_BT1)/(2*K);
sf_BT1_AV=sum(sf_BT1)/(2*K);
subplot(3,2,5);
plot(lags,rx_BT1_AV);title('基于BT法的Welch分段平均的自相关函数');
subplot(3,2,6);
plot(lags1,sf_BT1_AV);title('基于BT法的Welch分段平均的功率谱密度');grid on;
axis([0 +inf -inf +inf]);
3.MTM法
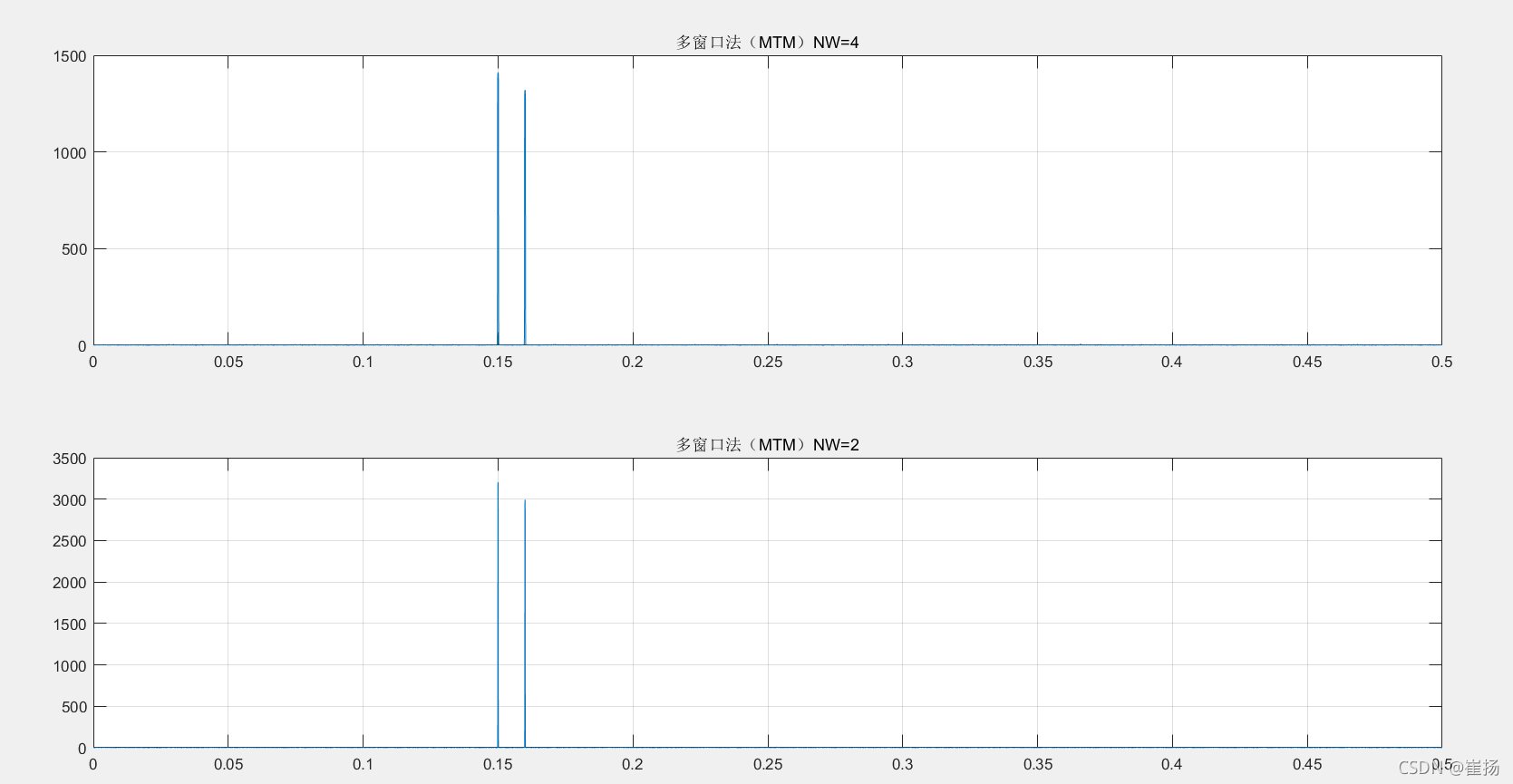
MTM法也称多窗口法,它没有使用带通滤波器,而是使用一组最优滤波器来计算估计值,这些最优FIR滤波器是由一组离散扁平类球体序列(DPSS,也叫Slepian)得到的。
在函数中,MTM提供了一个时间-带宽参数(时间和带宽的乘积NM),我们可以用它来平衡方差和分辨率。NM越大,会有更多的功率谱估计值,方差会越小。每一组数据都可以根据自己的需求,找到最适合的参数来平衡方差和分辨率。
%% MTM法
clc;clear all;close all;
N=20000; Nfft=20000; Fs=1; n=0:N-1;
x=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));
[pxx1,f]=pmtm(x,4,Nfft,Fs);
figure;
subplot(2,1,1);plot(f,pxx1);title('多窗口法(MTM)NW=4');grid on;
[pxx2,f]=pmtm(x,2,Nfft,Fs);
subplot(2,1,2);plot(f,pxx2);title('多窗口法(MTM)NW=2');grid on;
总结
可以根据以上三种方法的功率谱看出:
1.基于BT法的估计质量最差(怪不得没有函数表示基于BT法),并且当N减小到2000,不能分别出两个频率(可以复制后改值验证)。MTM法的估计质量最优。
2.Bartlett平均法和Welch平均法分段段数不同,但是效果相差不是很大,但是pwelch函数里窗函数的点数会影响分辨率。