[人工智能] ?【信号隐藏】基于奇异值分解svd和小波变换算法求解水印嵌入提取matlab代码

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> ?【信号隐藏】基于奇异值分解svd和小波变换算法求解水印嵌入提取matlab代码 -> 正文阅读

[人工智能]?【信号隐藏】基于奇异值分解svd和小波变换算法求解水印嵌入提取matlab代码

1 简介

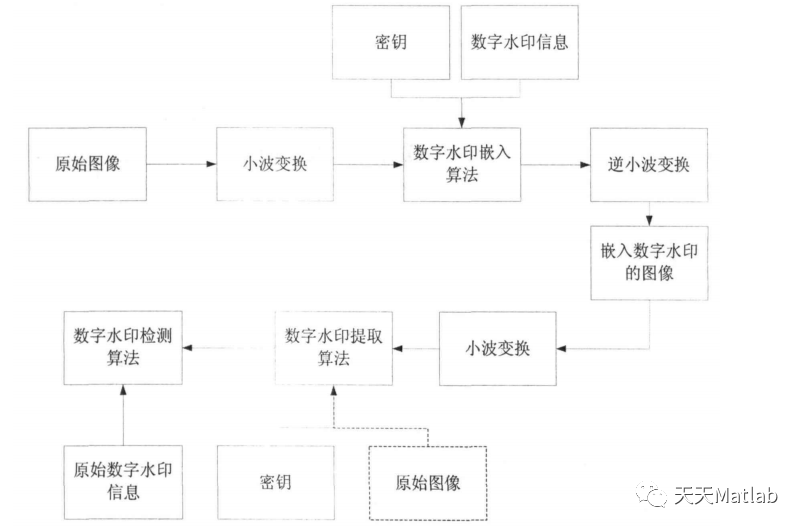
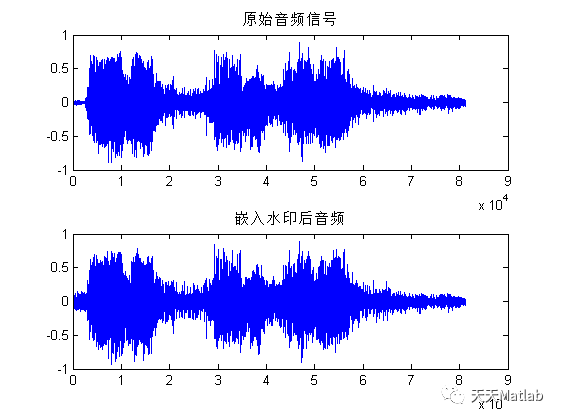
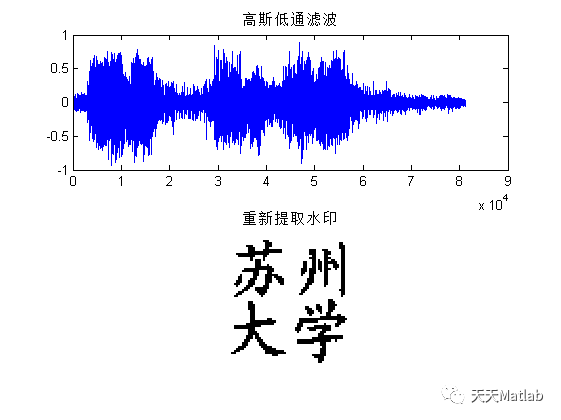
针对现有水印算法在嵌入过程中通常会对原始音频信号产生破坏的问题,设计了一种基于离散小波变换-奇异值分解(DWT-SVD)的水印嵌入方法实现水印信号的嵌入与提取.同时,以相关系数和误码率为衡量指标,对水印算法的不可感知性,安全性及鲁棒性进行评定测试.结果表明:在经过噪声,滤波,剪切,压缩等多种攻击后,所提取的水印仍然能保持较高的清晰度,这说明DWT-SVD算法具有较强的抗攻击能力,可有效保护版权人的利益.

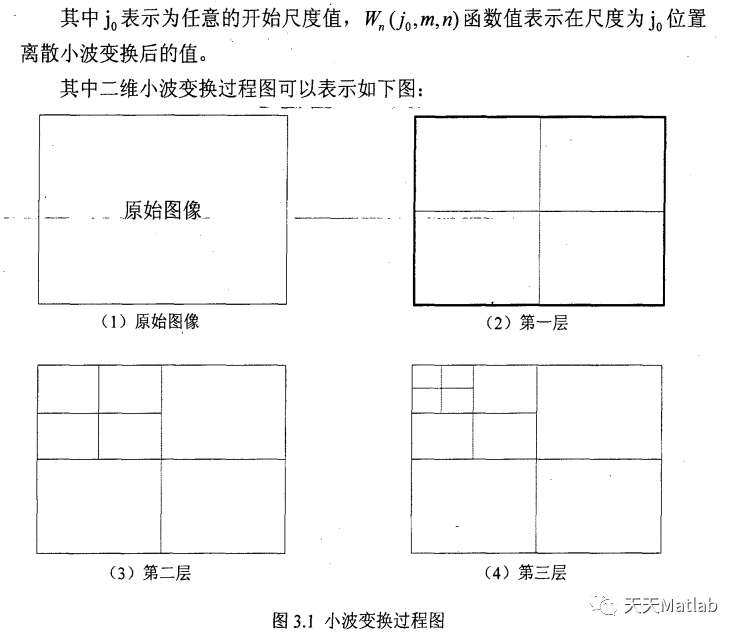
从小波变换的发展进程可知?,?小波变换理论基础是从傅里叶变换理论演变过来的?,?也可说小波变换是傅里叶变换的改进?。下面介绍的小波变换理论很?多都会利用的傅里叶理论系数?,?其小波变换展开式与傅里叶序列展开式很相似?。?首先介绍下小波函数公式

2 部分代码

function?exteredmark=extract(MarkedX,wrow,wcol)
%水印提取----------------------------------------
[cm,lm]=wavedec(MarkedX,2,'db4');?%用db4小波对读入的声音文件进行2级小波分解?
cma2=appcoef(cm,lm,'db4',2);?%提取2级小波分解的低频系数和高频系数?
cmd2=detcoef(cm,lm,2);?
cmd1=detcoef(cm,lm,1);?
lcma=length(cma2); ?%低频长度
blocksize=fix(lcma/(wrow*wcol));?%每块的大小
water_exter=zeros(1,wrow*wcol); ?%建立一个一维向量存储提取的水印信息
a=0.25; ?%量化步长
j=1;
for?i=1:wrow*wcol
? ?Blockm=cma2(j:j+blocksize-1);
? [UM,SM,VM]=svd(double(Blockm)); ??%对每块进行SVD变换
? ?if(mod(round(SM(1,1)/a),2)==0) ?%如果为靠近步长的偶数倍，则水印信号为0
? ? ? ?water_exter(i)=0;
? ?else
? ? ? ?water_exter(i)=1; ? ?%如果为靠近步长的偶数倍，则水印信号为0
? ?end?
? ?j=j+blocksize;
end
exteredmark=reshape(water_exter,wrow,wcol);