写在前面
这次是李宏毅机器学习组队学习的第三次打卡任务,学习误差和梯度下降的内容,之前也是了解过一些,但是理解不渗透,这次好好总结一下。
参考视频:https://www.bilibili.com/video/av59538266
参考笔记:https://github.com/datawhalechina/leeml-notes
误差的来源
从上一节的回归的例子可以看出来,Average Error 随着模型复杂程度呈指数型增加,其来源主要是bias和variance。
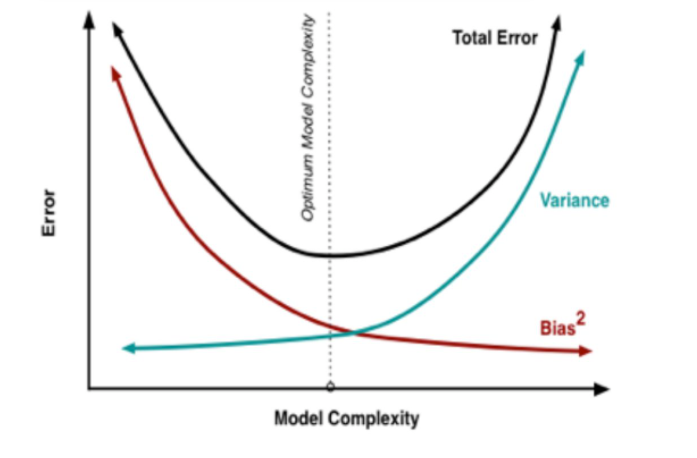
bias 描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单的说,就是在样本上拟合的好不好,想要在bias上表现得好,就得复杂化模型,增加模型的参数,但这样容易过拟合(overfitting),过拟合对应的是high variance.
varience描述的是样本上训练出来的模型在测试集上的表现,想要在variance上表现好,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应的是high bias。
估测变量x的偏差和方差
误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方
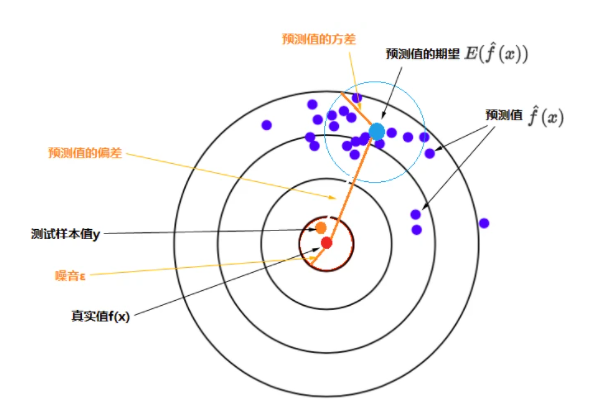
靶心(红点)是测试样本的真实值,测试样本的y(橙色点)是真实值加上噪音,特定模型重复多次训练会得到多个具体的模型,每一个具体模型对测试样本进行一次预测,就在靶上打出一个预测值(图上蓝色的点)。所有预测值的平均就是预测值的期望(较大的浅蓝色点),浅蓝色的圆圈表示预测值的离散程度,即预测值的方差。
所以,特定模型的预测值 与 真实值 的误差的 期望值,分解为上面公式中的三个部分,对应到图上的三条橙色线段:预测值的偏差、预测值的方差、样本噪音。
评估x的偏差
假设 x 的平均值是 μ \mu μ,方差为 σ 2 \sigma^2 σ2
评估平均值做法:
- 首先拿出N个样本点: x 1 , x 2 , ? ? , x N {x^1, x^2, \cdots, x^N} x1,x2,?,xN
- 计算平均值
m
m
m,如果计算很多组
m
m
m,求得
m
m
m的期望:
E [ m ] = E [ 1 N ∑ x n ] = 1 N ∑ n E [ x n ] = μ E[m] = E[\frac{1}{N}\sum x^n] = \frac{1}{N} \sum_n E[x^n] = \mu E[m]=E[N1?∑xn]=N1?∑n?E[xn]=μ
m
m
m分布对于
μ
\mu
μ 的离散程度(方差):
V
a
r
[
m
]
=
σ
2
N
\mathrm{Var[m]} = \frac{\sigma^2}{N}
Var[m]=Nσ2?
这个取决于 N,下图看出 N 越小越离散:
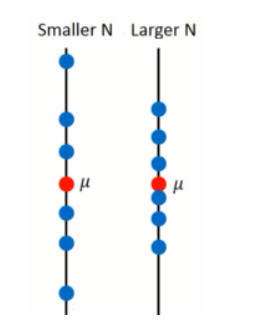
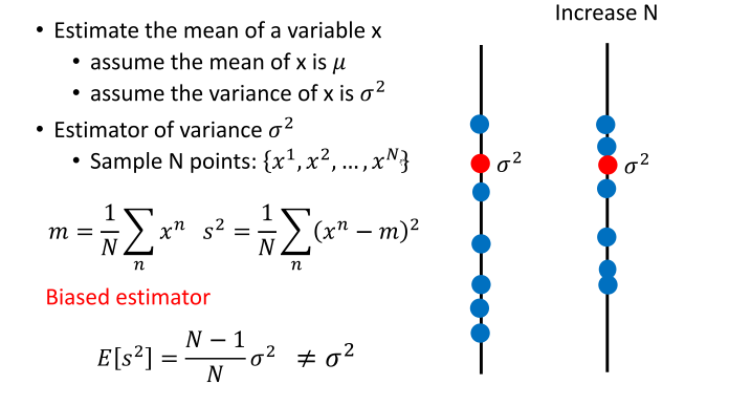
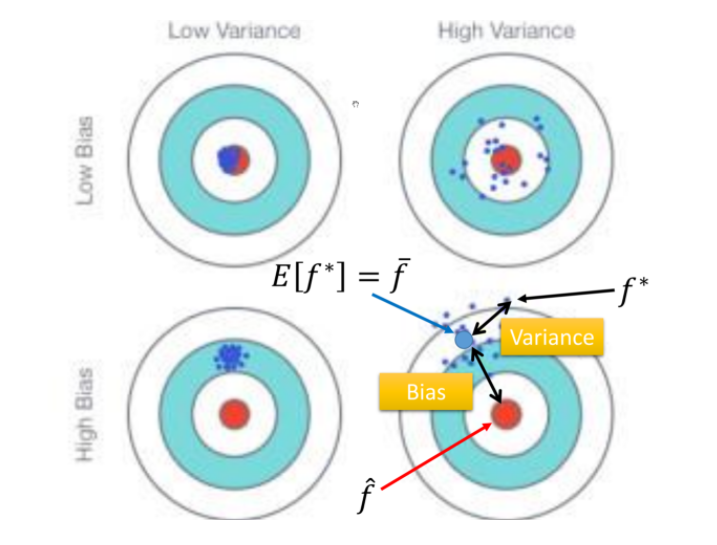
当模型足够复杂的时候,通常会体现出high variance:
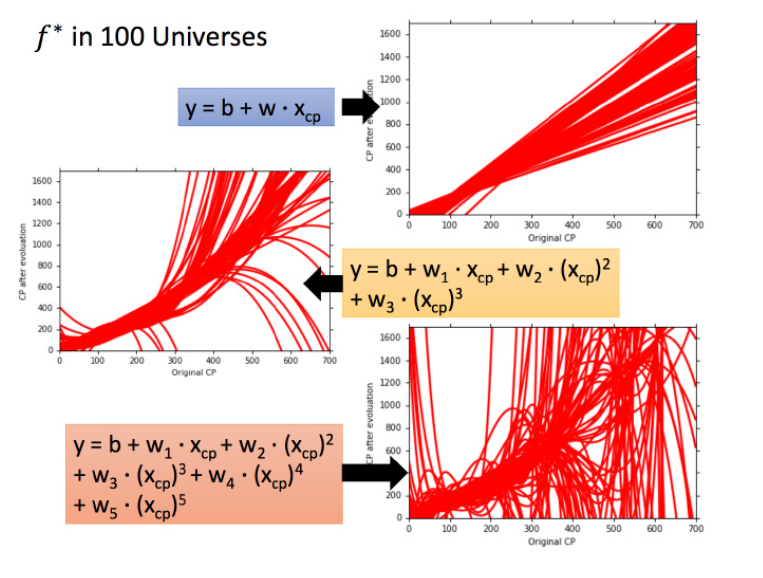
一次模型的方差就比较小的,也就是是比较集中,离散程度较小。而5次模型的方差就比较大,同理散布比较广,离散程度较大。
考虑不同模型的偏差
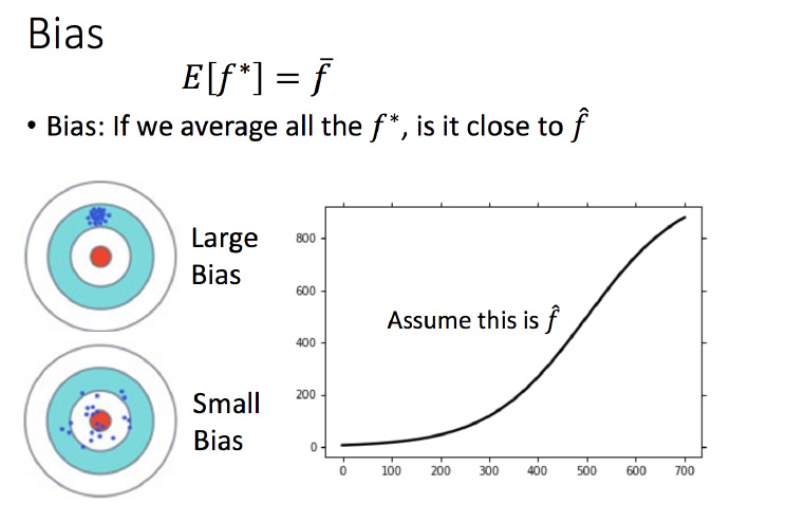
这里没办法知道真正的 f ^ \hat{f} f^? ,所以假设图中的那条黑色曲线为真正的 f ^ \hat{f} f^? 结果可视化,一次平均的 f ˉ \bar{f} fˉ? 没有5次的好,虽然5次的整体结果离散程度很高。一次模型的偏差比较大,而复杂的5次模型,偏差就比较小。
偏差v.s.方差
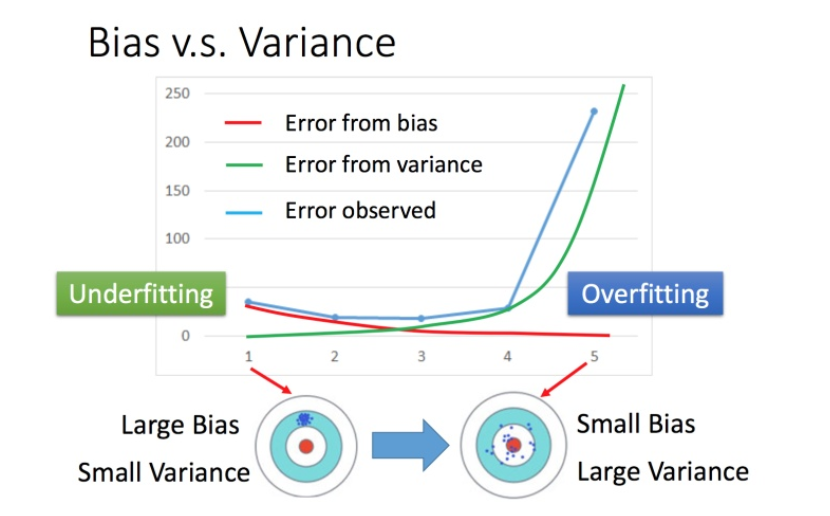
如何判断过拟合还是欠拟合
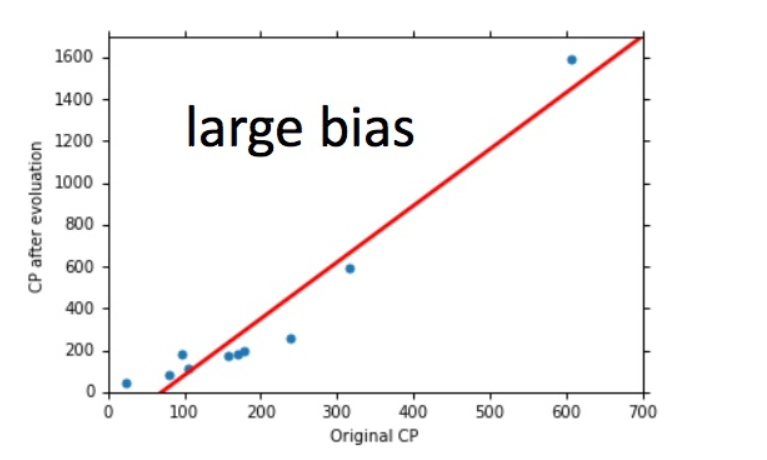
如果模型没有很好的训练训练集,就是偏差过大,也就是欠拟合 如果模型很好的训练训练集,即再训练集上得到很小的错误,但在测试集上得到大的错误,这意味着模型可能是方差比较大,就是过拟合。 对于欠拟合和过拟合,是用不同的方式来处理的。
偏差大-欠拟合:重新设计模型
方差大-过拟合:增加数据量,加强对整体分布的捕捉,减少落在局部的可能性。
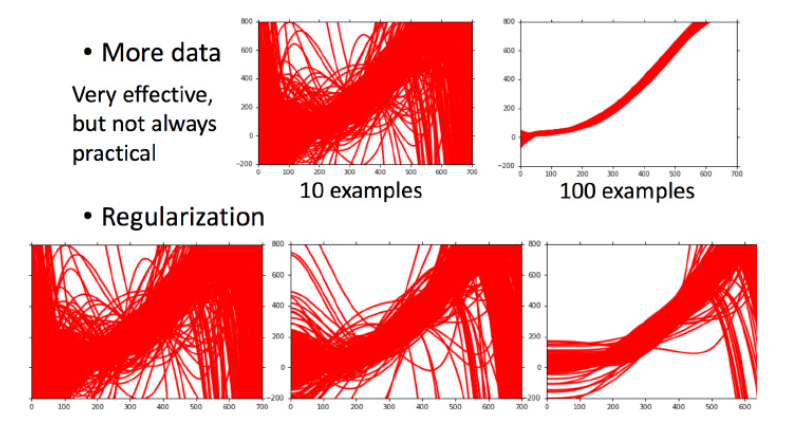
交叉验证
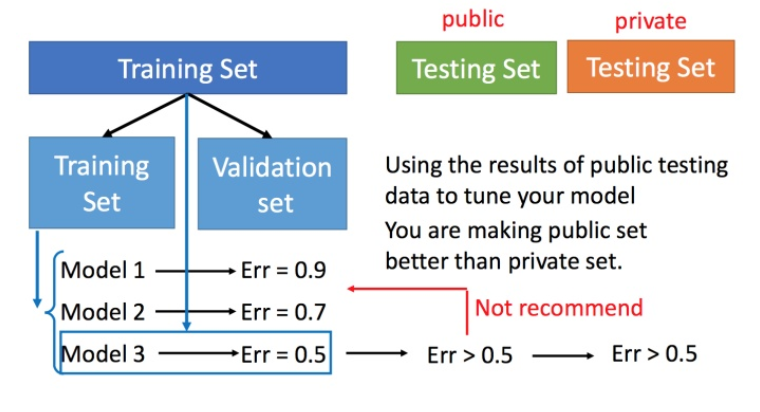
图中public的测试集是已有的,private是没有的,不知道的。交叉验证 就是将训练集再分为两部分,一部分作为训练集,一部分作为验证集。用训练集训练模型,然后再验证集上比较,确实出最好的模型之后(比如模型3),再用全部的训练集训练模型3,然后再用public的测试集进行测试
N-折交叉验证
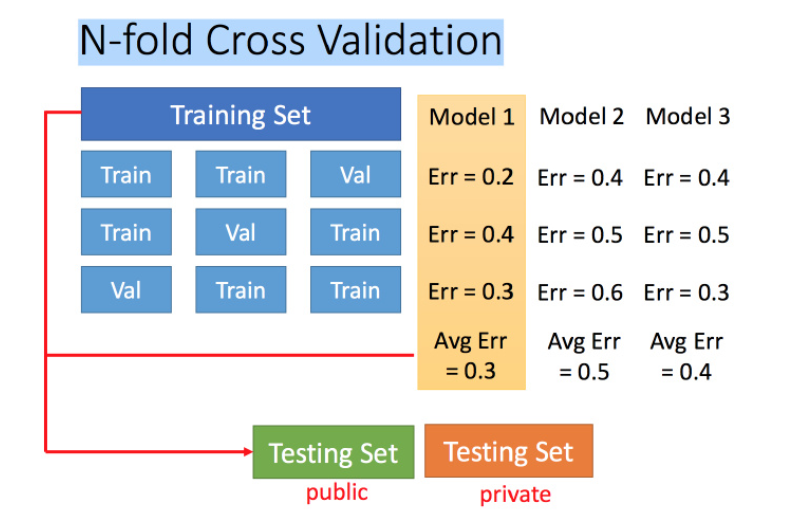
比如在三份中训练结果Average错误是模型1最好,再用全部训练集训练模型1
梯度下降法
在回归问题的第三步中,需要解决下面的最优化问题:
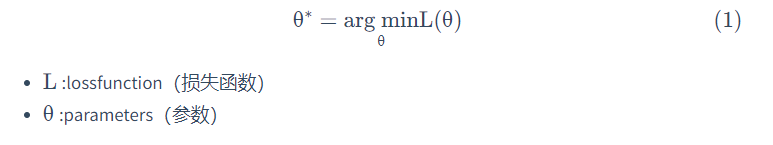
照一组参数
θ
\theta
θ,让损失函数越小越好,这个问题就可以用梯度下降法解决:

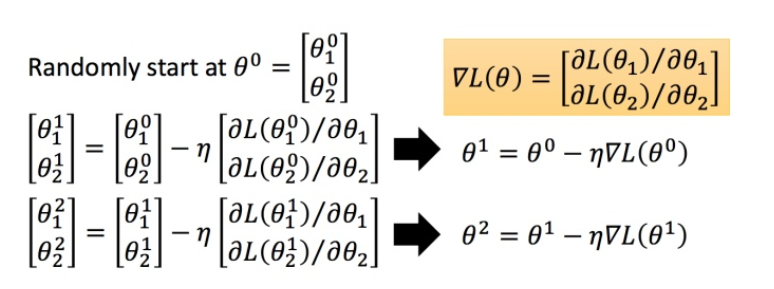
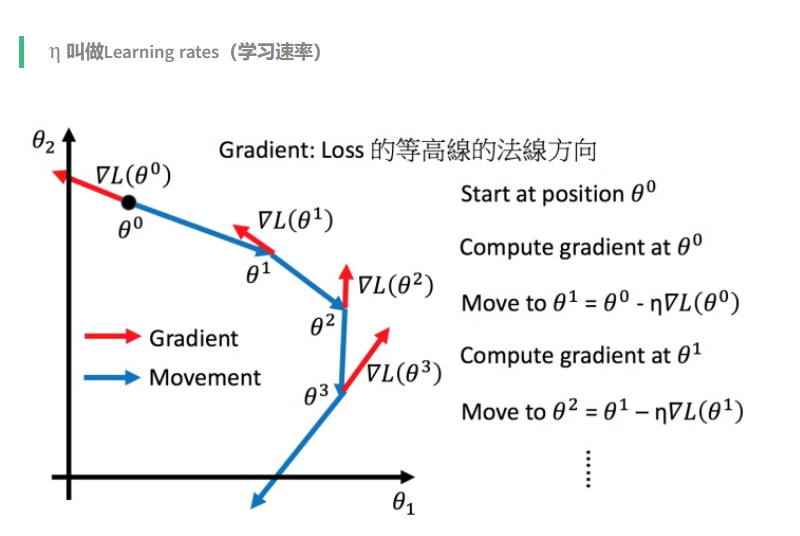
自适应学习率
举一个简单的思想:随着次数的增加,通过一些因子来减少学习率
-
通常刚开始,初始点会距离最低点比较远,所以使用大一点的学习率
-
update好几次参数之后呢,比较靠近最低点了,此时减少学习率
-
比如 η t = η t t + 1 \eta^t = \frac{\eta^t}{\sqrt{t + 1}} ηt=t+1?ηt?, t t t是次数,随着次数的增加, η t \eta^t ηt减少。
Adagrad算法
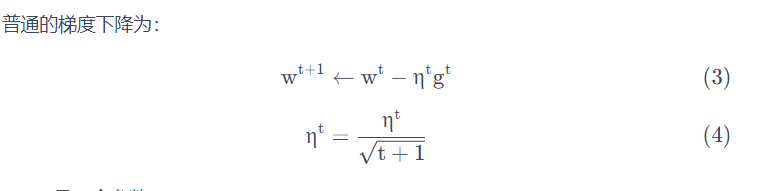
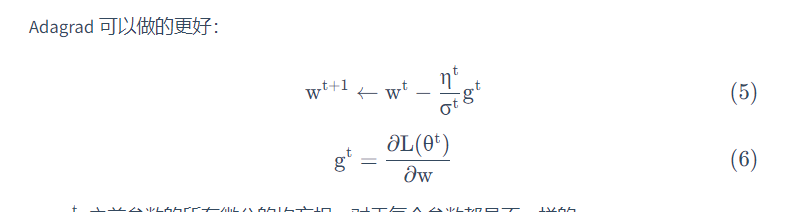
例子:
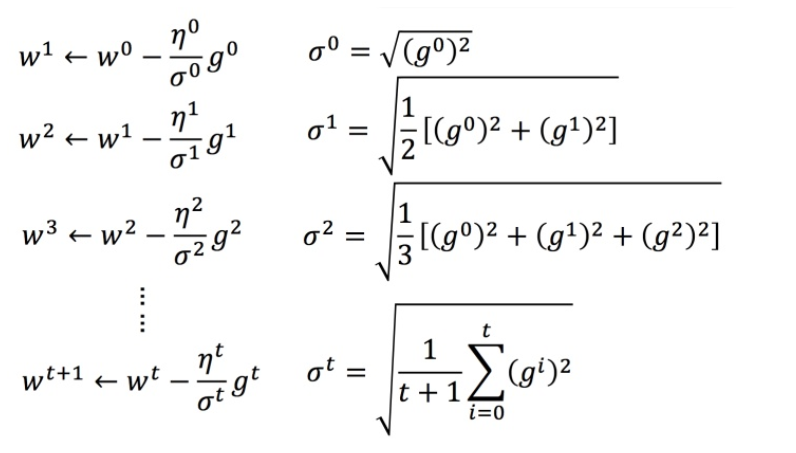
对其化简,有KaTeX parse error: Expected '}', got 'EOF' at end of input: …^t (g^i)^2} g^t
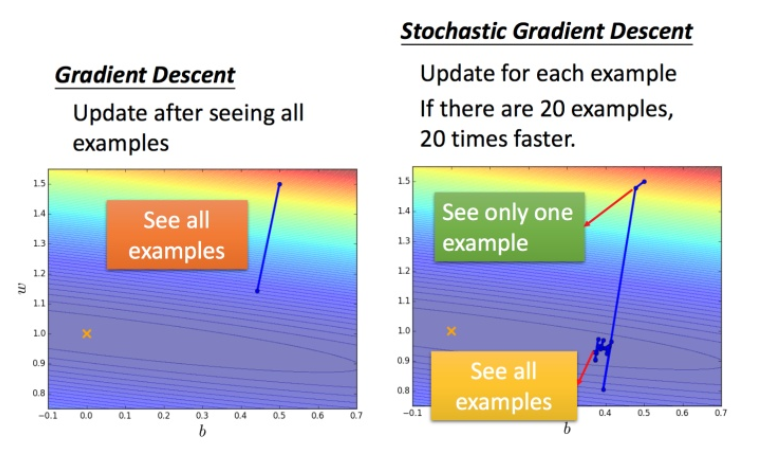
随机梯度下降法
之前的梯度下降:
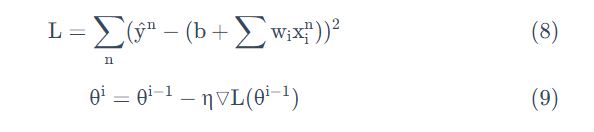
而随机梯度下降法:
损失函数不需要处理训练集所有的数据,选取一个例子
x
n
x^n
xn
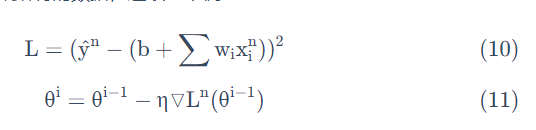
对比:
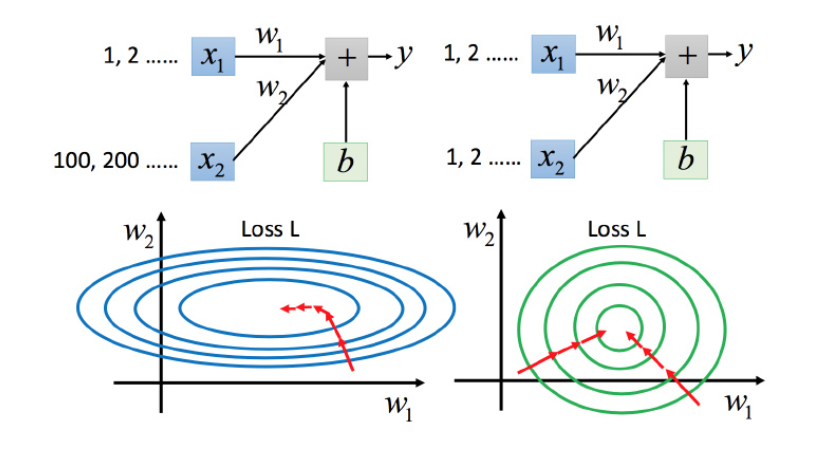
特征缩放
假设有个函数:

两个输入的分布的范围很不一样,建议把他们的范围缩放,使得不同输入的范围是一样的。
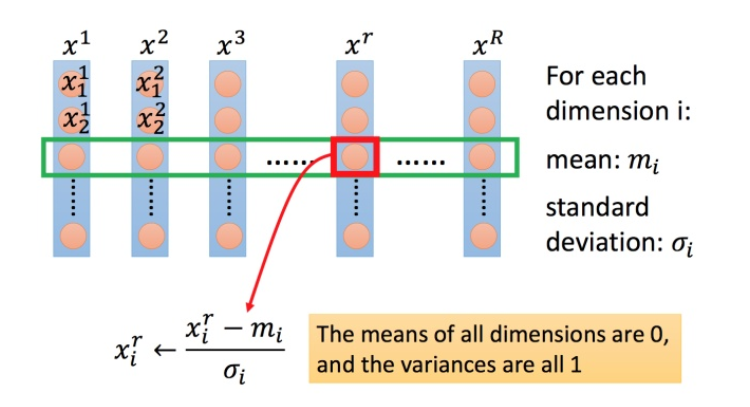
标准化缩放特征:
梯度下降的理论基础

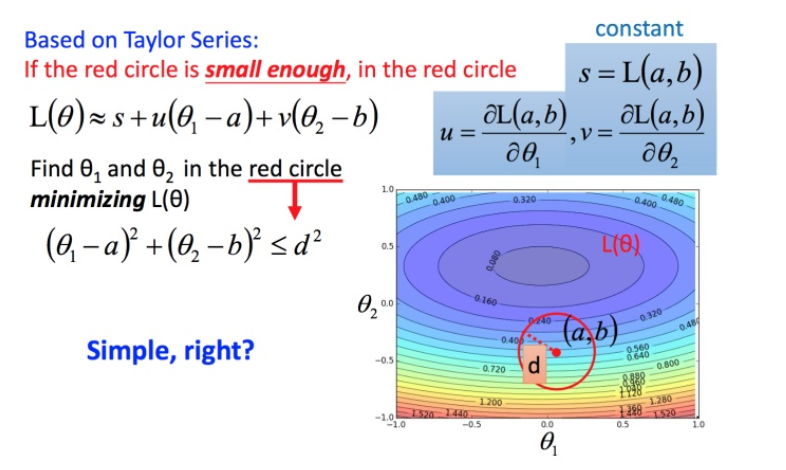
利用泰勒展开式简化
回到之前如何快速在圆圈内找到最小值。基于泰勒展开式,在 (a,b)(a,b) 点的红色圆圈范围内,可以将损失函数用泰勒展开式进行简化:

将问题进而简化为下图:
不考虑s的话,可以看出剩下的部分就是两个向量
(
Δ
θ
1
,
Δ
θ
2
)
(\varDelta \theta_1, \varDelta \theta_2)
(Δθ1?,Δθ2?)和 (u,v)(u,v) 的内积,那怎样让它最小,就是和向量 (u,v)(u,v) 方向相反的向量
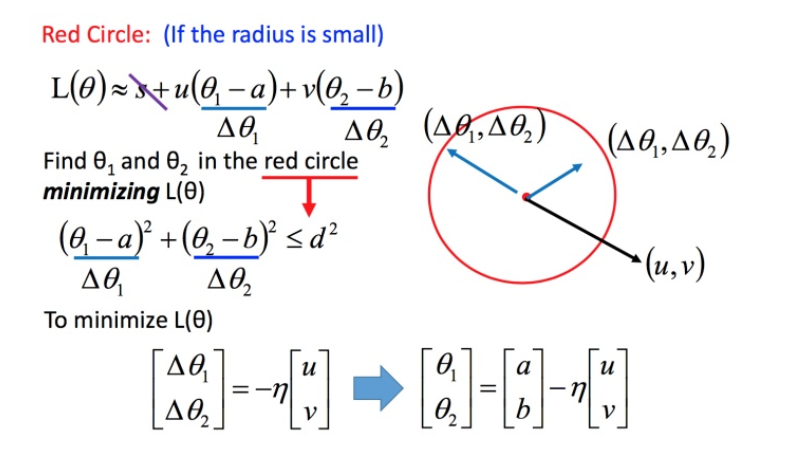
然后将u和v带入:

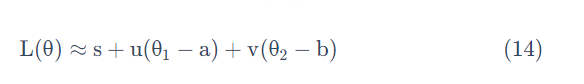
发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提,泰勒展开式给的损失函数的估算值是要足够精确的,而这需要红色的圈圈足够小(也就是学习率足够小)来保证。所以理论上每次更新参数都想要损失函数减小的话,即保证式1-2 成立的话,就需要学习率足够足够小才可以。
梯度下降的限制
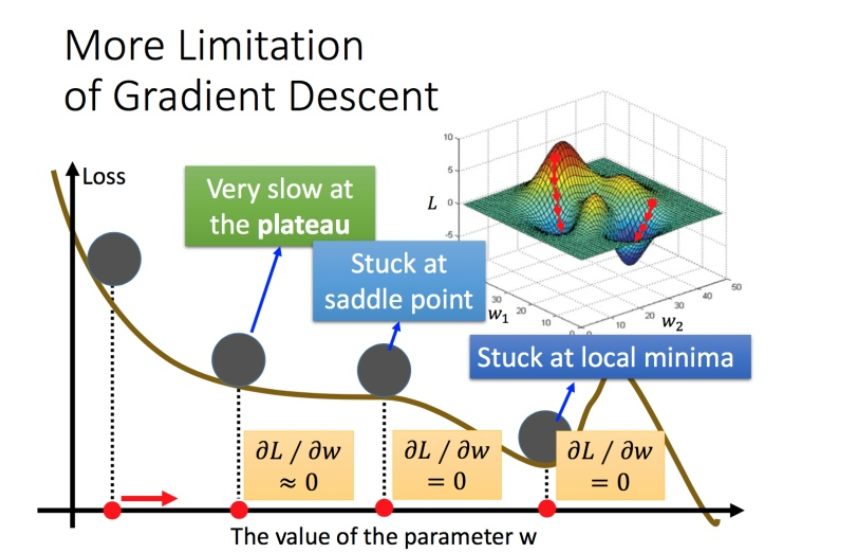
容易陷入局部极值 还有可能卡在不是极值,但微分值是0的地方 还有可能实际中只是当微分值小于某一个数值就停下来了,但这里只是比较平缓,并不是极值点。