scipy.stats.norm函数
可以实现正态分布(也就是高斯分布)
pdf ——概率密度函数标准形式是:
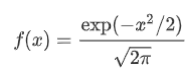
norm.pdf(x, loc, scale)等同于norm.pdf(y) / scale ,其中 y = (x - loc) / scale
stats.norm主要公共方法如下:
rvs:随机变量(就是从这个分布中抽一些样本)
pdf:概率密度函数。
cdf:累计分布函数
sf:残存函数(1-CDF)
ppf:分位点函数(CDF的逆)
isf:逆残存函数(sf的逆)
stats:返回均值,方差,(费舍尔)偏态,(费舍尔)峰度。
moment:分布的非中心矩。
归一化数据
机器学习模型被互联网行业广泛应用,一般做机器学习应用的时候大部分时间是花费在特征处理上,其中很关键的一步就是对特征数据进行归一化。
归一化后加快了梯度下降求最优解的速度;如果机器学习模型使用梯度下降法求最优解时,归一化往往非常有必要,否则很难收敛甚至不能收敛。归一化有可能提高精度;一些分类器需要计算样本之间的距离(如欧氏距离),例如KNN。如果一个特征值域范围非常大,那么距离计算就主要取决于这个特征,从而与实际情况相悖(比如这时实际情况是值域范围小的特征更重要)。
标准化的流程简单来说可以表达为:将数据按其属性(按列进行)减去其均值,然后除以其方差。最后得到的结果是,对每个属性/每列来说所有数据都聚集在0附近,方差值为1。
作用:去均值和方差归一化。且是针对每一个特征维度来做的,而不是针对样本。
标准差标准化(standardScale)使得经过处理的数据符合标准正态分布,即均值为0,标准差为1,其转化函数为:
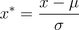
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。