这是我在csdn上面的第1篇博文,以前做了一些东西,尤其是机器学习和神经网络方面的。但考虑到时间原因,再加上大学带读比较忙,一直没有时间写。今天写出我的第1篇博文,是以后想常开这个栏目,相当于我的专题吧。会经常的找一些控制类的,机器学习和神经网络算法类的,包括我本专业通信领域相关的论文进行详细解读,并且对于研究方向进行思考。
GAN领域相关的研究要从Goodfellow在2014年发表在arXiv上的这篇论文开始,自此以后GAN成为了神经网络领域可以说研究最热门的一个方向,这几年来有不下上万份的研究聚焦于无监督学习的对抗生成网络,而在实际应用中,GAN也被广泛应用于二维重建,三维重建等等方向。
下面开始我对GAN领域这篇开山之作的论文详细精读。



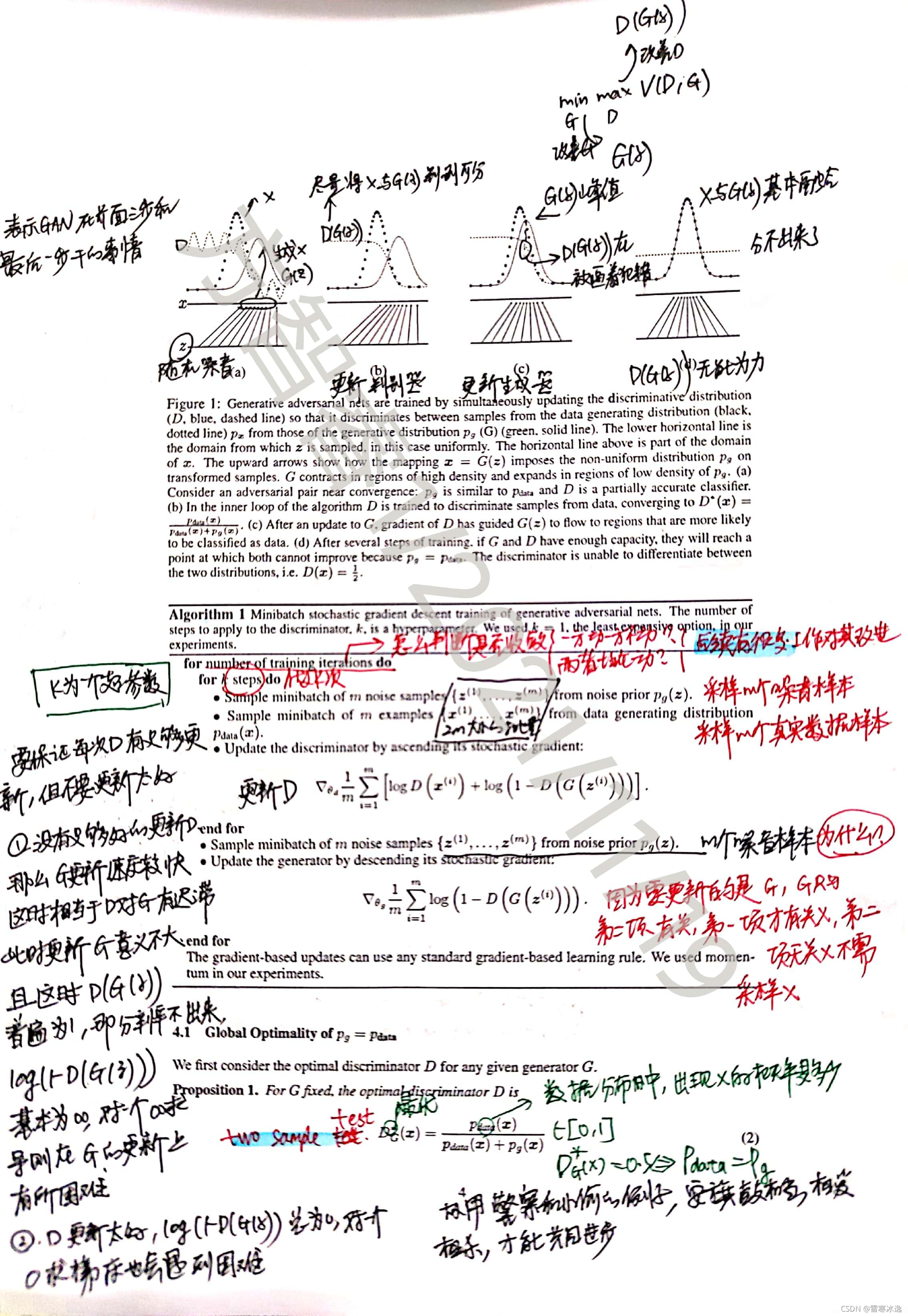





这篇论文实际上也提出了GAN网络研究领域内的相关困难,论文中最为凸显的留待后人工作解决的问题。主要是生成器G和判别器D的协同(同步性)问题,以及相对于G而言,D过强或过弱带来梯度消失或爆炸问题(论文中称为海奥维提卡现象,在中科院自动化所对于GAN网络的专栏论文集里,广泛讨论了这种现象,并把其翻译为模式崩溃问题)。
下面结合近段时间我的论文研读和研究方向,说出几点思考:
对于GAN网络的损失函数,最初的也是最为原始的,在这篇论文中提出了两个期望相加和并且形象的把它称之为“凹凸博弈”问题。实际上由于损失函数是对数期望函数,造成了判别函数有关项和生成函数有关项(相对于第1项只与判别函数有关而言),也就是第1项和第2项,分别是凹函数和凸函数,如何在凹函数和凸函数的竞争博弈中选取最小值被称为竞争博弈问题。但是论文中也提到了一个在训练刚开始的时候,由于两个网络当中有一个刚开始的能力过弱,我们会将其中一个log(1-G)那一项先写作log(G)进行训练,所以在刚开始的时候造成了"凹凹博弈"问题,同时即使我们规避了传统的模式识别当中,对于分布用一系列的分布函数去近似,而改用直接用参数去学习这样的分布(或者论文中采用非参数估计当中的Parzen窗方法),在WGAN(GAN的一种变体)的一些工作中规避掉了用对数式函数作为损失函数而采用最简单的f(x)=x作为惩罚函数,但即使这样,即使我们保证D和G都是线性的情况下,我们也不能保证当函数套函数的时候生成的函数还能保持原函数的凹性或凸性(全局上)。(这是我的理解昂,最近我也在看相关的论文,在WGAN的一些文章中,把凹凸博弈拓展到了凹凹博弈进行研究,给出的原因就是在大多数情况下都不满足凹凸博弈这样一个强假设。),而且即使是一个or函数和一个凸函数相加生成的函数,我们也不能保证它的全局凹形和凸性,这时候用于一种更通俗易懂语言来讲的话,我们就要比较一下两个函数在哪个地方的凹性或者是凸性更强,这有可能是凹凸博弈成为一个强假设条件的原因吧。
最后特别鸣谢课题组李文学老师,在您的讨论班和研究方向中我初步接触了GAN网络,您的讨论班对于我理解干函数也产生了深刻的影响,并且引导我对于你目前正在研究的方向进行继续的思考和研究。