目录
1 图像特征
试想,从不同的距离,不同的方向、角度,不同的光照条件下观察一个物体时,物体的大小、形状、明暗都会有所不同。但我们依然可以判断它是同一个物体。 这是因为什么呢?因为特征!
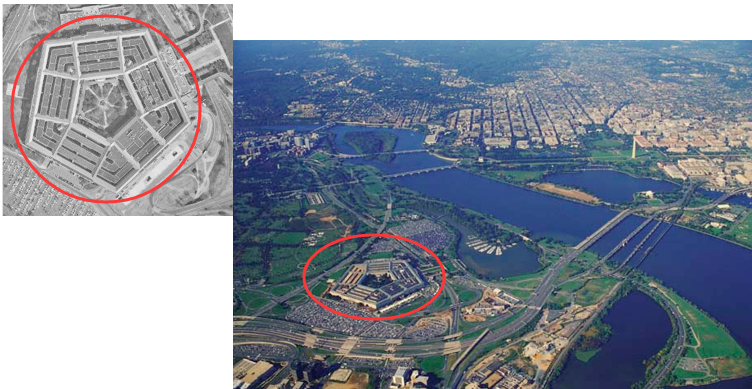
计算机视觉中常用的图像特征包括:点、边缘、以及特有的组件等等。
而其中点特征(不是指像素点,而是指图像中一个小局部)在视觉的各种任务中非常有用,如全景拼接、运动跟踪、物体识别等等。
为什么选择图像的点特征?
答:点特征作为图像特征之一的优势如下:
- 提取具有可重复性和准确性
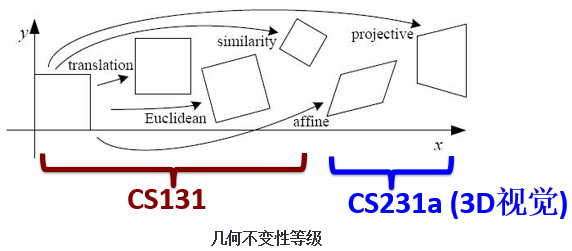
- 不受图像平移、旋转、缩放变化的影响
- 对仿射变换也较为鲁棒
- 抗光照变化,噪声,模糊,量化
-
- 局部性:点特征属于局部特征,所以对图像遮挡有一定鲁棒性;
- 数量:通常图像中可以检测到成百上千的点特征,以量取胜;
- 辨识性:点特征有较好的辨识性,不同物体上的点容易区分;
- 效率:点特征提取通常速度很快;
?
一个基于特征点来实现图像匹配的神奇例子:


2 点特征——Harris角点
Harris算子是一种点特征提取算子,哈里斯+史蒂芬斯于1988年提出(是对Moravec角点检测算子的改进)。
2.1 角点
角点就是图像的“角落”位置,也是灰度值会发生突变的位置。“角点”特征相比“边缘”特征而言,在辨识性和信息量方面都具备很多优势,看下面这张图,你就知道为什么“角点”是一种好的特征。
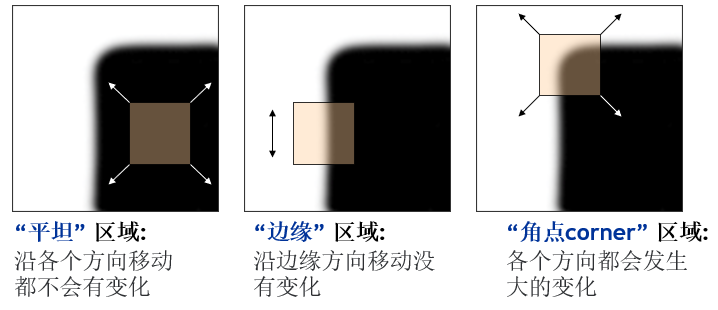
如上图,当我们用一个窗口去和图像局部区域像素进行例如累加求和操作时,仅在“角点”位置其计算结果会与其临近的其他位置计算结果差异都比较大。
2.2 数学描述
为了得到角点的精确位置,以及量化是否是角点的概率值,需要对角点进行明确的数学描述。关于角点的上述性质的数学建模如下:
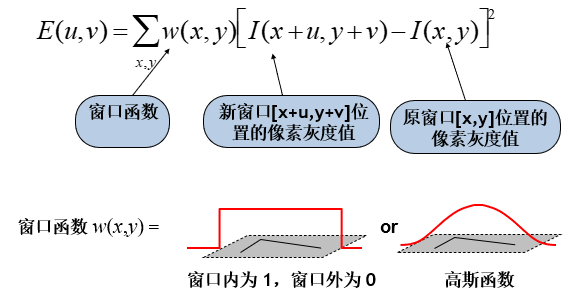
- I(x, y)是:窗口移动前所覆盖的原图区的x,y位置的灰度值。注意:这个x,y坐标是相对此处这个窗口的坐标系而言,而元素值是图像的灰度值而不是窗口函数内元素值。
- I(x+u, y+v)是:窗口在图像上移动[u, v]个单位后所覆盖的原图区的位置的灰度值,这个x,y同样是相对窗口的坐标系。
- W(x, y)是:窗口函数,也就是权重系数,比如一个元素值全1的矩阵窗口,或者高斯核窗口。
- 遍历x,y累加求和中的x,y是什么:这里的x,y指的是窗口尺度的大小,假如窗口大小是10x10像素,那么公式里就要累加100个像素点位置的差值和。
- E(u, v)是:简单说,E是一个二维矩阵,它存储的是窗口在图像上平移前后内部元素灰度值变化的差值。具体说,窗口在图像上平移[u, v]后,新窗口区域内像素值和平移之前窗口内像素值的对应位置的差的平方再乘以权重系数再累加之和。描述的有点拗口,语言不好整理,看下面这个可视化例子解释:

假设左边这个大图是某图像的一个局部区域,红色框是我们用于判定图像此处是否有角点的窗口,它是个初始位置。E(3, 2)意思是,这个红色窗口,移动[3,2]个单位,到达图像中绿色框位置,然后把两个框内像素的灰度值一个个的代入到上述公式中去计算加权累加和。
有个点注意:
- E(0, 0)必定为0,即窗口没移动,所以对应位置像素值差全为0。
- E(u, v)中元素值越大,代表两个位置窗口内情况差异越大。
- Moravec角点检测用的全1权重窗口,而Harris角点检测用的高斯核窗口(中心点附近的差值权重大,边缘点附近的差值给的权重少)。
接下来不要忘记一个很重要的点(不然后面公式推导看不懂目的):角点处是滑窗往任意方向移动变化量都大。所以,如果一个窗口内有角点,那么这个窗口往四周滑动计算出的 E(u, v) 矩阵,其除了E(0, 0)位置之外,E(u, v)矩阵中其他位置的元素值,必须都要足够大才行,有任何一个位置点值不大,都表示很可能不是角点了。
2.3 公式推导
为了能够直接观察到E(u,v)与[u,v]之间的联系,根据泰勒展开式,对公式推导优化如下:(https://zhuanlan.zhihu.com/p/90393907)

上述公式汇总,Ix, Iy是某个像素位置的图像偏导值。对它们的一些直观印象可如下:

如何通过矩阵判断角点的?
其实上面,我们已经推导出E(u,v)的表达式,大家看看这个表达式有什么特征,其中矩阵H是实对称矩阵,那么E表达式其实就是二次型,对于二次型想必大家会有印象,U,V代表窗口滑动方向以及滑动量,E代表灰度变化,通过矩阵M进行特征值求解,而特征值所对应的特征向量即为灰度变化方向。如果两个特征值较大,则表示有两个方向灰度变化较快。所以可以直接通过求解H的特征值进行角点判断。
如果线性代数知识忘了,可以看下面这种可视化解释:
2.4 公式的物理意义
考虑下面这种角点情况:
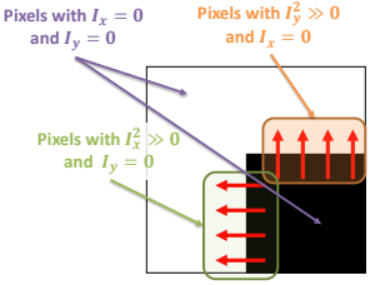
哈里斯矩阵可以简化为一个对角矩阵(主对角线之外的元素皆为0的矩阵):
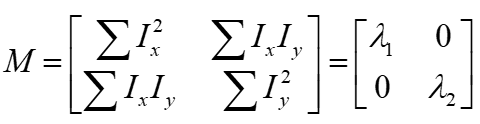
原因:上图那种情况,每个像素点位置,其x、y方向的偏导,必定至少有一个方向的偏导为0,所以x方向偏导乘以y方向偏导其值一定为0,所以累加结果也一样为0。
?这意味着:如果任何一个λ接近0,那么这就不是一个角,所以我们应该寻找两个λ都很大的图像窗口。
当然实际上,角点方向是随意的,哈里斯矩阵一般是这样:
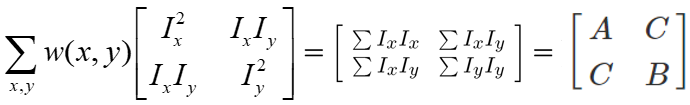
但是,根据线性代数知识,一个实对称矩阵,有下面这种性质:

R是正交矩阵(旋转矩阵),而旋转矩阵的逆和旋转矩阵自身的转置相等,进一步化简E(u,v)有:
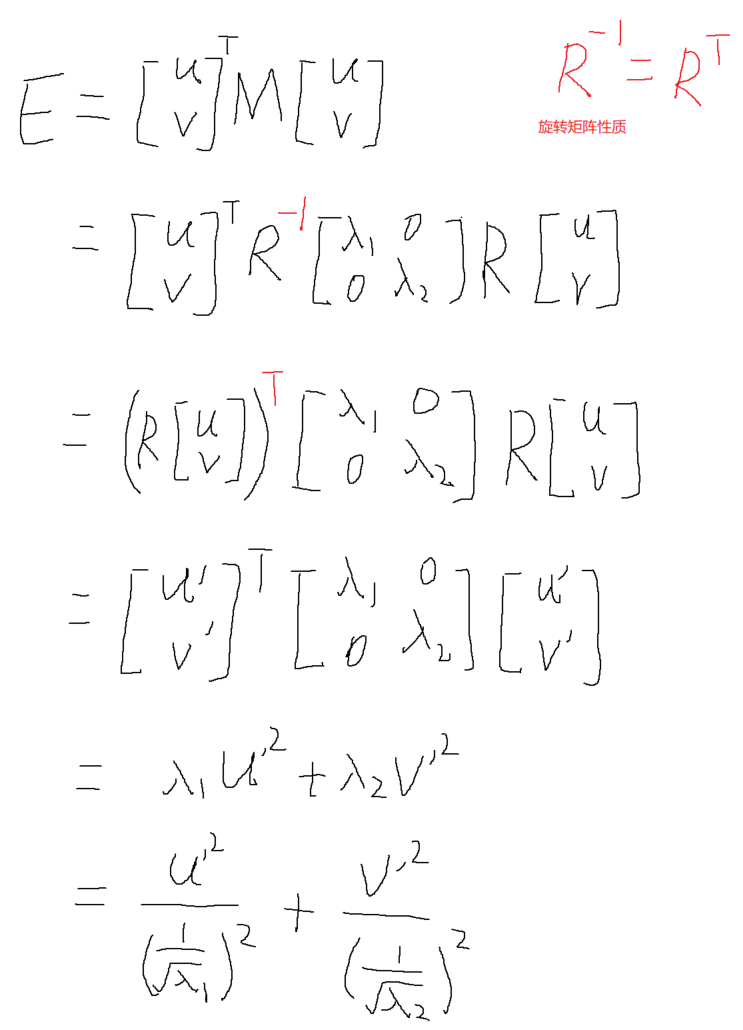
上公式中,u'和v'相当于对u,v坐标系旋转了一定角度。而实际上,一个角点旋转后,还是个角点,与旋转无关,所以,我们判定是否是角点可以只要关注λ1和λ2。
上述公式表面,E(u, v),u, v三者在立体空间中是一个椭圆关系,如下:
(3D绘图软件:https://www.geogebra.org/calculator)
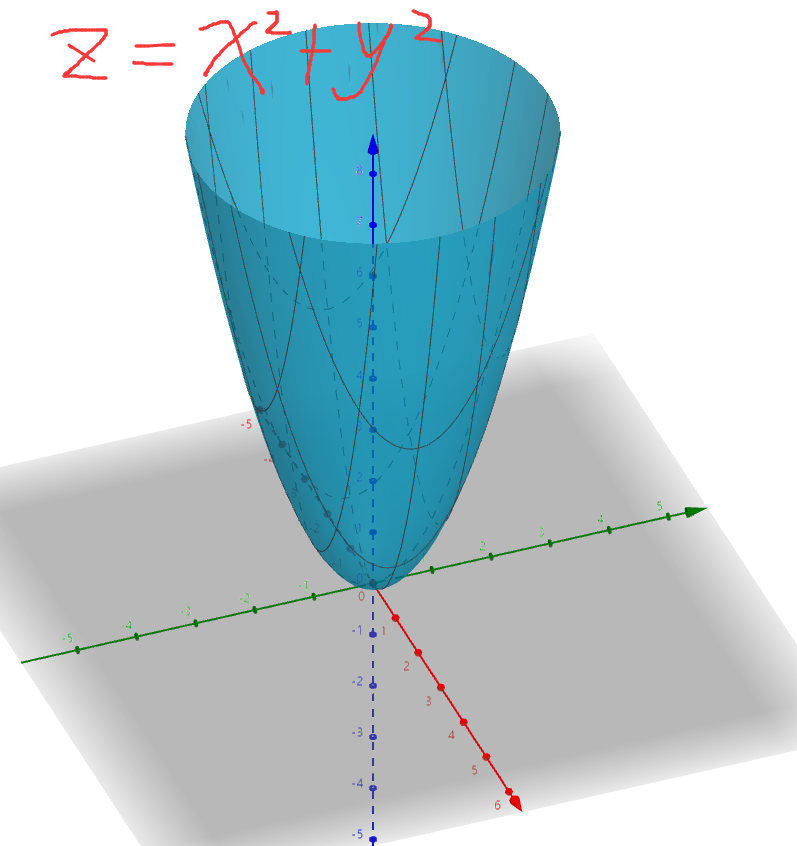
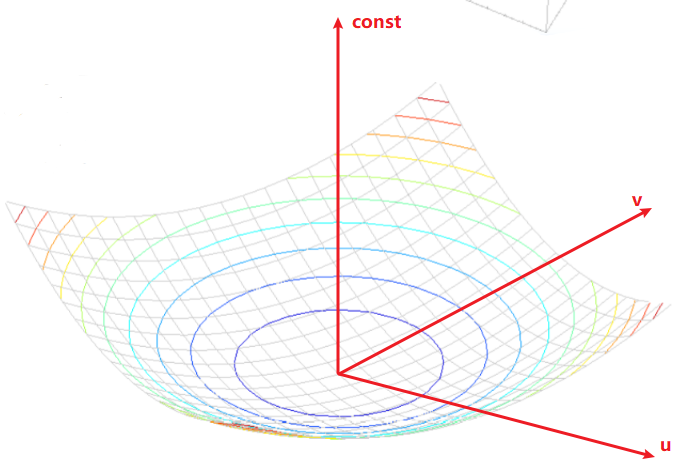
如上图,要使E(u,v)中u,v取任何值,都要相对E(0, 0)位置差异越大越好,则λ1和λ2要同时足够大。因为根据最终推导出的公式,只有它们同时足够大,这个空间中形成的椭球,相对u,v平面就会越陡峭,无论u,v往那个方向移动,E值都变化很大。
具体来说,λ1和λ2两者取不同范围值时,窗口内分别是“平坦区”或“角点”或“边缘”的情况:
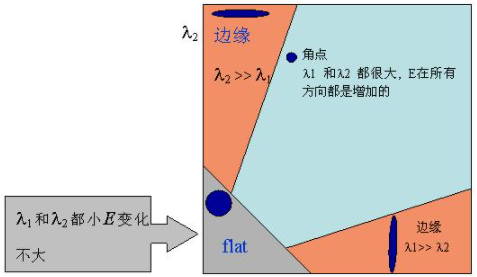
为了进一步用公式表示上述现象,也为了方便计算,Harris角点检测中采用如下角点响应函数(不是仅有这样才行)来直接判定一个位置是否为角点:
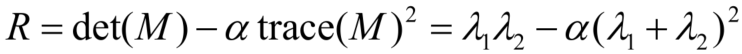
其中,α是个常量取值在[0.04, 0.06]。
即现在变成:(当然R也可以设定大于一个其他固定阈值)
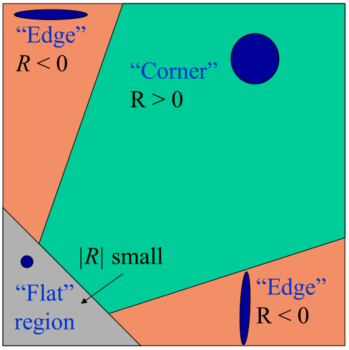
为什么会使用这样的角点响应函数?
(https://blog.csdn.net/lwzkiller/article/details/54633670)
答:Harris也许对很多函数模型非常了解,对于创造出这样的一个函数表达式,易如反掌。这个角点响应函数画出来如下:
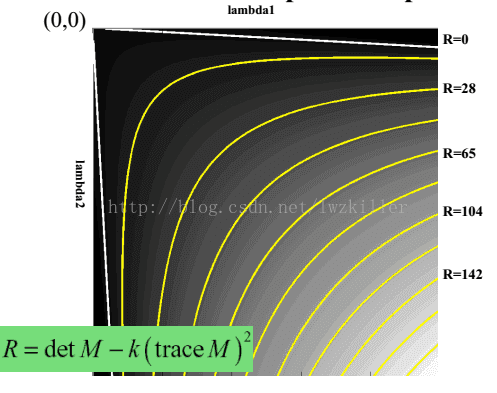
刚好符合对λ1和λ2的要求:
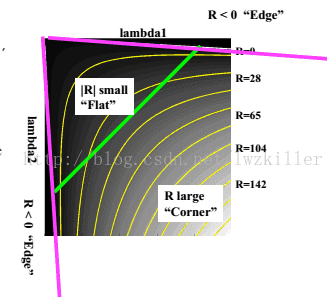
2.5 算法流程
- 滤波、平滑,避免出现阶跃函数。
- 计算图像梯度。
- 计算每个像素位置的Harris矩阵M。
- 计算每个像素位置的角点响应函数R。
- 设置门限R,寻找响应函数的局部最大值(非最大抑制)。
2.6?检测效果
原图

响应函数R:(颜色越暖,代表该像素点位置R结果越大)
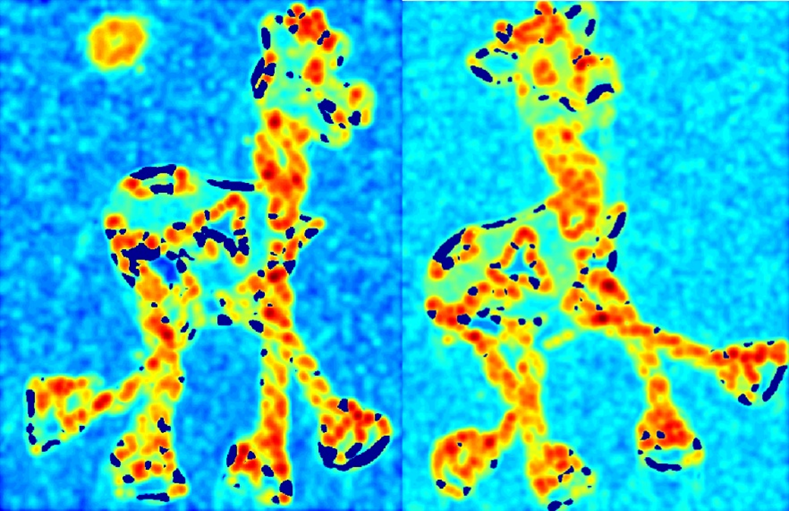
对R设置阈值:

仅保留局部最大的点(非极大值抑制):

最终效果图:

其他场景的检测效果图:
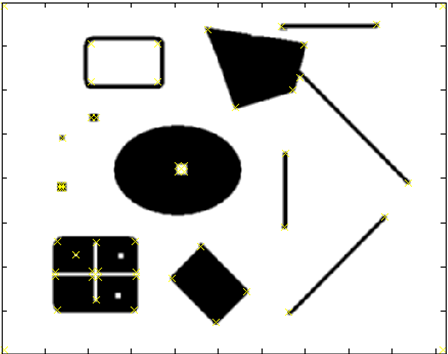


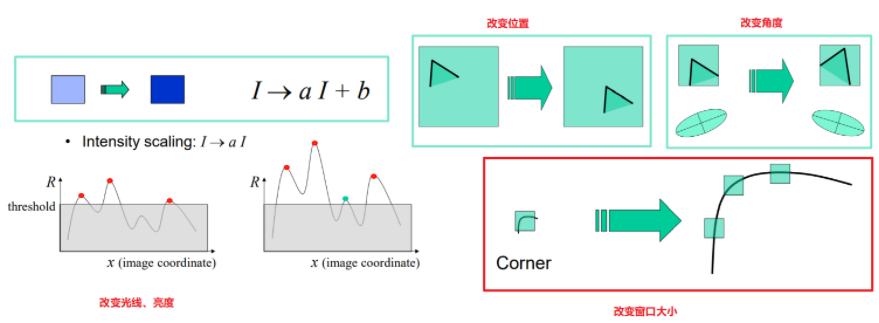
2.7 Harris角点性质
- 当光线强度,明暗改变时,只是改变了部分角点的值,还有大部分的点可以用于检测,可以进行检测。
- 平移和旋转位角度时,可以检测。
- 当改变窗口大小时,大窗口下是角点,而小窗口下是线或者边缘,无法检测。