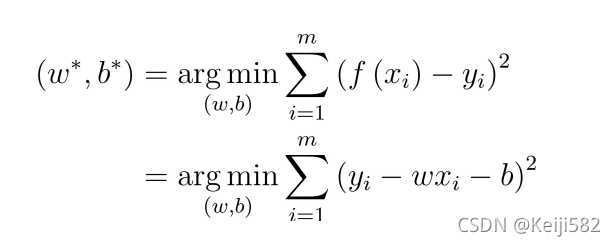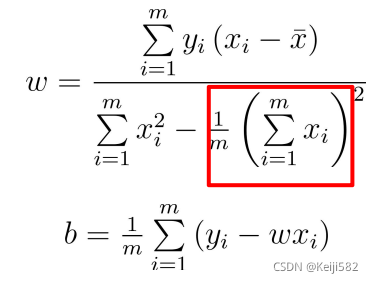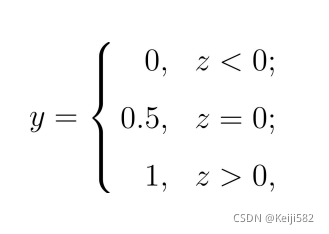[人工智能]logistic回归

实验环境

Python:3.7.0
Anconda:3-5.3.1 64位
操作系统:win10
开发工具:sublime text(非必要)

实验简介

本次实验为学习和了解机器学习中应用到的线性模型和其中的经典案例logistic回归，并且以UCI的数据集完成一个分类任务。

线性回归

在直接引入**对数几率回归（即logistic回归）**前，更为合适的方式是先介绍线性回归
首先，线性模式一般的形式如下：

其中x=(x1, x2, …, xd)是由d维属性描述的样本，其中 xi 是 x 在第 i 个属性上的取值。

同时，也可以用向量形式写成

首先需要理解，线性回归本身完成的是一个回归任务，即试着学习一个线性模型来尽可能的预测出输出值；也就是学习到上面的w的权值矩阵和偏移量b，从而达到可以依靠一个x来获得一个预测的y值，并使得这个y值尽可能的逼近真实值。

为了使得整个概念简单易懂，我们先模拟一种最简单的情况，即输入属性只有一个，也就是只有w1和b需要被预测。这个时候我们简单的写一个简短的demo进行测试。（注意：这里使用到了Sklearn库）

Sklearn (全称 Scikit-Learn) 是基于 Python 语言的机器学习工具。它建立在 NumPy, SciPy, Pandas 和 Matplotlib 之上，里面的 API 的设计非常好，所有对象的接口简单，很适合新手上路。

且为了使得模型简单易懂，设计了一个大致是w1为2，b为0的模型对象，并手动以这个目标为前提设计了一个简易的数据集。

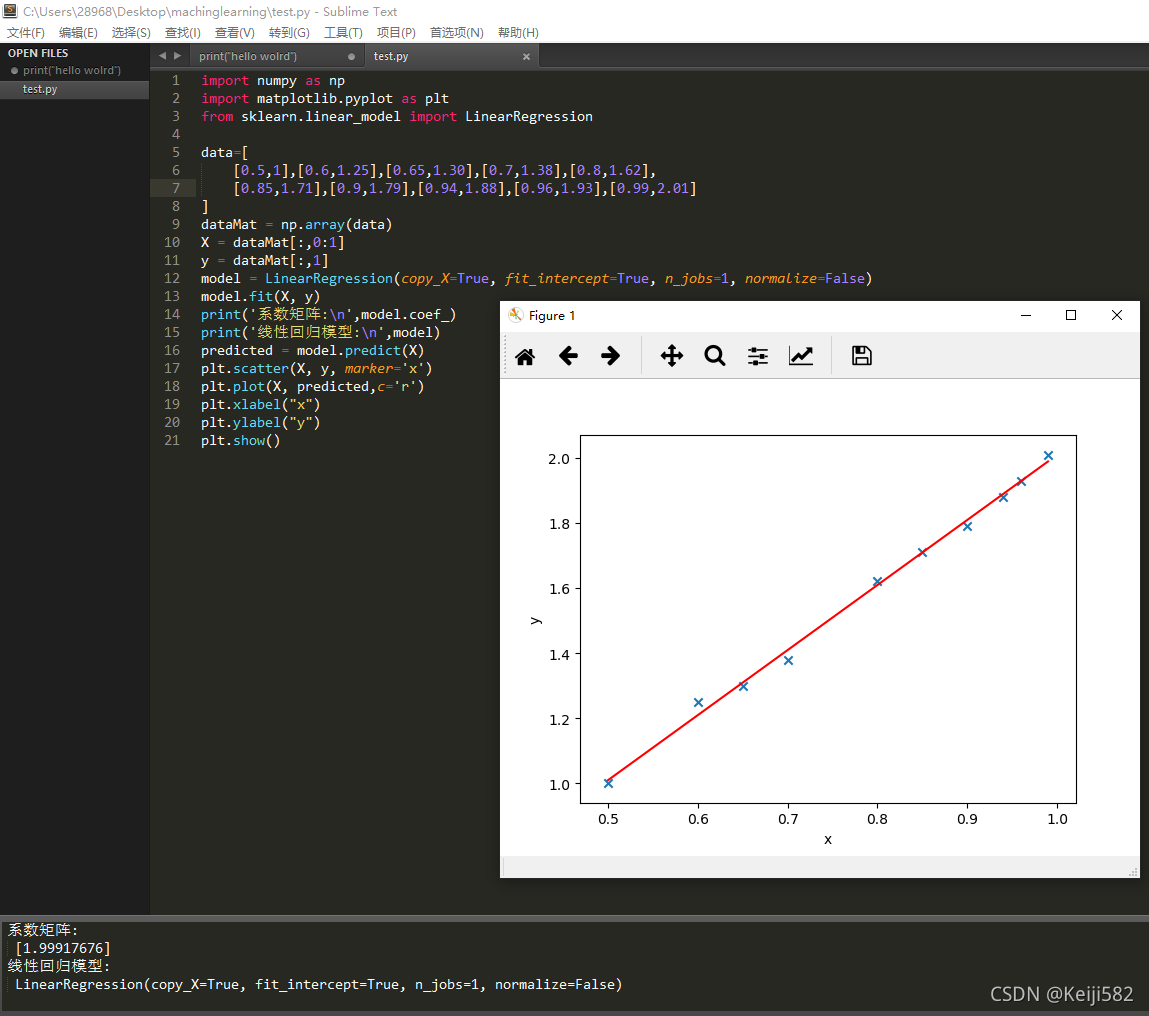
import numpy as np 
import matplotlib.pyplot as plt  
from sklearn.linear_model import LinearRegression

data=[
    [0.5,1],[0.6,1.25],[0.65,1.30],[0.7,1.38],[0.8,1.62],
    [0.85,1.71],[0.9,1.79],[0.94,1.88],[0.96,1.93],[0.99,2.01]
]
dataMat = np.array(data)
X = dataMat[:,0:1] 
y = dataMat[:,1]   
model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X, y) 
print('系数矩阵:\n',model.coef_)
print('线性回归模型:\n',model)
predicted = model.predict(X)
plt.scatter(X, y, marker='x')
plt.plot(X, predicted,c='r')
plt.xlabel("x")
plt.ylabel("y")
plt.show()

让我们实际观察运行结果

最小二乘与参数求解

事实上，如果囫囵吞枣的看完上面的内容和实验结果后，也许会觉得不难理解，但仔细看看就会觉得有许多费解之处，这是由于上面的例子用了完成度很高的Sklearn库，大量的相关操作已经在这个库内包含完成了；也就是下面这两行。

model = LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
model.fit(X, y)

但这里有一点需要注意的是，对于整个过程而言，参数到底是如何求得的？这个才是整个算法的关键，这里会引入一个最小二乘的概念。

首先，为了确定w和b，一定程度上需要确定f（x）和y的差别，这里会涉及到均方误差的概念。
这里引用一篇优秀的相关博文，需要了解相关概念的可以前往阅读。

https://blog.csdn.net/qq_38701868/article/details/99703998

也就是上面的形式，这里的w和b表示w和b的解；在这里，基于均方误差最小化来进行模型求解的方法就被称为“最小二乘法”。换言之，线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上得欧式距离最小。

显而易见的，我们可以分别对w和b求导并使得各自结果为0可以得到最优解的闭式解

这个过程不难推导，只要有简单的高数基础就可以完成；其中图中画红线的部分其实就是x的均值。

但同样有一个重要的问题，即上述的情况只涉及一个属性，而实际情况中往往存在多个属性。这时我们试图学习的便不再是一个单值的w，而是一个向量。

类似的，可以利用最小二乘法来对w和b进行估计，为了方便表述，将w和b使用向量形式，相应的，把数据集表示为一个m*（d+1）大小的矩阵X，其中每行对应于一个示例，该行前d个元素对应于示例的d个属性值，也即是下图中的红框部分，并将最后一个元素值1，如下

再将y也做类似的操作

则此时依据前面最小二乘的形式可以相似的得出下列式子

同时我们令Ew等于上式并对w进行求导可得

对数几率回归

经过前面的引入后，我们已经可以简单的理解使用线性模型进行回归任务；但如果我们要进行的是分类任务该怎么办？其实很简单，只要将广义线性模型（式子如下）的微调函数进行适当的选择即可。

这里需要进行一个简单的补充，虽然本实验为logistic回归（也即对数几率回归），但实际上解决的是分类任务，名字中的回归指的是回归分界线，也即回归的是参数。

考虑二分类的任务，其输出要么为1要么为0，而线性回归模型产生的预测值是连续的实值；于是我们需要将结果进行转换。最理想的方法是一个简单的单位阶越函数如下

但上面的函数有一个巨大的缺陷，即其是不可导的非连续函数，显然这在上面的广义线性模型中不能充当联系函数的职位，因为需要求导。

相对应的，我们提出了一个替代的解决方案，也就是至今仍在各种机器学习模型中应用的sigmoid函数。

它的图像长这样

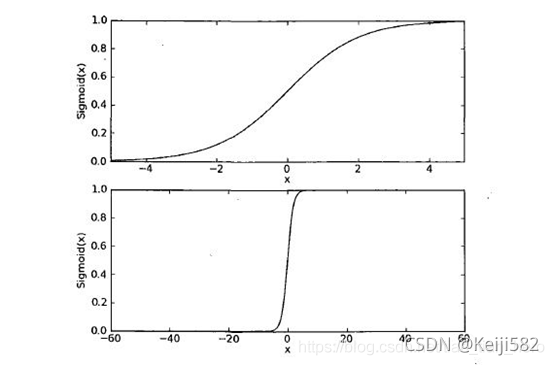
可以看到，虽然在小范围内看不出来，但稍微将范围扩大时，这个函数与阶跃函数高度相似。

为了获得最佳的回归系数w和b这里要用到最优化方法。在很多分类器中，都会将预测值与实际值的误差的平方和作为损失函数（代价函数），通过梯度下降算法求得函数的最小值来确定最佳系数。

我们需要先定义一个最大似然函数L，假定数据集中的每个样本都是独立的，其计算公式如下：

取似然函数的对数：

为了更好地理解这一最终损失函数，先了解一下如何计算单个样本实例的成本：

通过上述公式发现：如果y=0，则第一项为0；如果y=1，则第二项等于0；

接下来我们就要使用梯度下降求最小值了。首先，计算对数似然函数对j个权重的偏导：

计算sigmoid函数的偏导：

我们的目标是求得使损失函数最小化的权重w，所以按梯度下降的方向不断的更新权重：

由于我们是同时更新所有的权重的，因此可以将更新规则记为：

综上，我们将梯度下降的更新规则定义为：
但注意，后面的实验中采用的是，人民邮电出版社的《机器学习实战》的代码，其所使用的是梯度上升的方法，与此处的梯度下降相反，需要将上诉结果取反。

实验

注意，本次实验的代码为人民邮电出版社的《机器学习实战》所提供，书中代码为python2环境下的代码，有部分函数存在弃用，本实验在python3的环境下运行，会有部分修改。

数据集

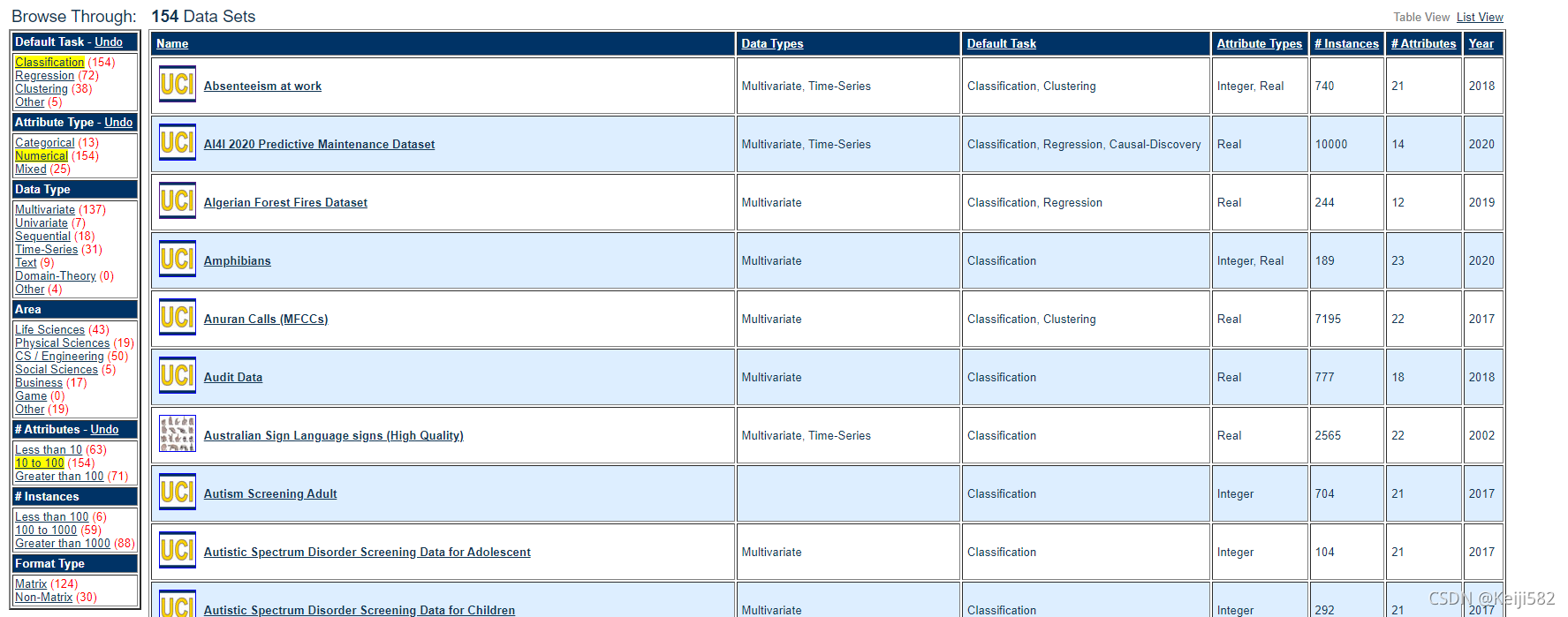
本次实验的数据集采用UCI机器学习数据库，其网址如下

https://archive.ics.uci.edu/ml/datasets.php

其中为了符合本次实验的需求，选取用于分类的数据集，并且属性在10个以上控制在100个以下。

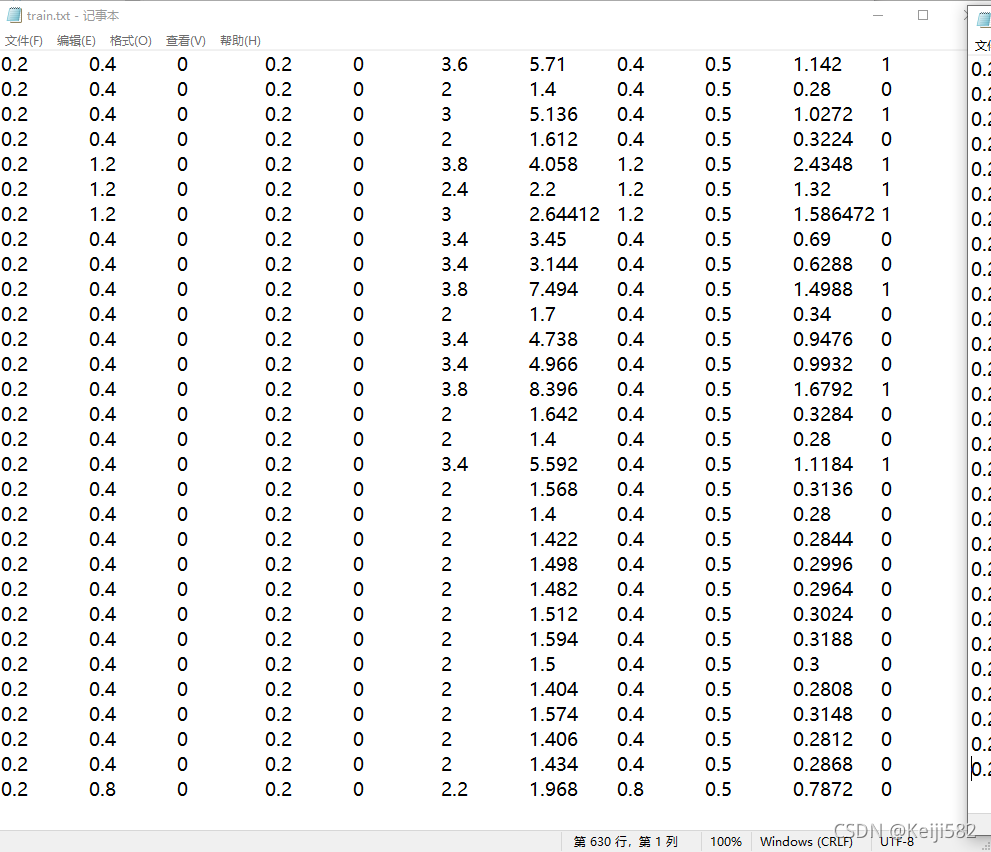
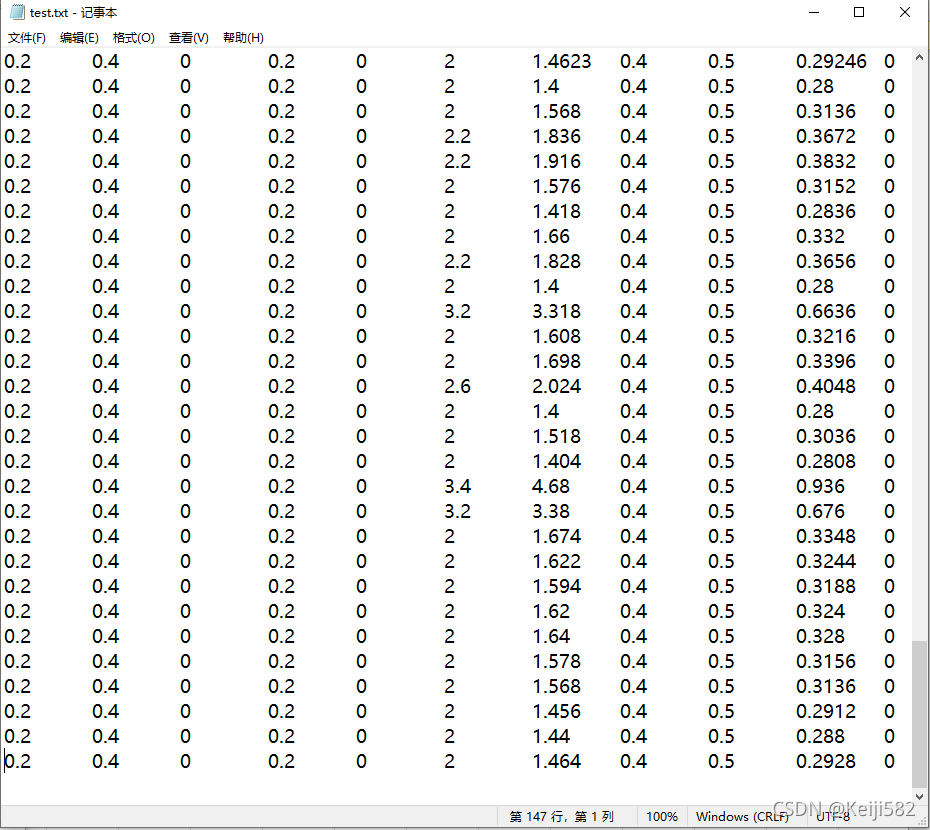
对选定的数据集进行人为的切分，所选用数据集属性为10，样本个数为776，切分后分别如下图所示

代码实现

首先是对sigmoid函数的实现 十分简单

def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

其次对梯度上升算法的实现

#改进的随机梯度上升法（随机化）
#使用随机的一个样本来更新回归系数
#numIter迭代
def stoGradAscent1(dataMatrix, classLabels, numIter = 150):
    #m为行 n为列
    m,n = shape(dataMatrix)
    weights = ones(n)
    # 随机梯度, 循环150,观察是否收敛
    for j in range (numIter):
        # [0, 1, 2 .. m-1]
        dataIndex = range(m)
        for i in range(m):
            #alpha会随着迭代次数不断减小，但不会是0
            alpha = 4 / (1.0 + j + i) + 0.0001
            # random.uniform(x, y) 方法将随机生成下一个实数，它在[x,y]范围内,x是这个范围内的最小值，y是这个范围内的最大值。
            randIndex = int(random.uniform(0, len(dataIndex)))
            #随机选取更新
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del (list(dataIndex)[randIndex])
    return weights

然后设计一个函数用回归系数和特征向量作为输入来计算对应的sigmoid值，大于0.5时返回1反之则返回0。

#输入：特征向量与回归系数
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    #大于0.5 返回 1；否则返回0
    if prob > 0.5:
        return 1.0
    else:
        return 0.0

然后是用于打开测试集和训练集的函数

def colicTest():
    frTrain = open('HorseColicTraining.txt')
    frTest = open('HorseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    # trainingSet 中存储训练数据集的特征，trainingLabels 存储训练数据集的样本对应的分类标签
    for line in frTrain.readlines():
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(10):
            lineArr.append(float(currLine[i]))
        #存入训练样本特征
        trainingSet.append(lineArr)
        #存入训练样本标签
        trainingLabels.append(float(currLine[10]))
    #使用改进后的随机梯度下降算法得到回归系数
    trainingWeights = stoGradAscent1(array(trainingSet), trainingLabels, 500)

    #统计测试集预测错误样本数量和样本总数
    errorCount = 0;
    numTestVec = 0.0
    for line in frTest.readlines():
        #循环一次，样本数加1
        numTestVec += 1.0
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(10):
            lineArr.append(float(currLine[i]))
        # 利用分类预测函数对该样本进行预测，并与样本标签进行比较
        if int(classifyVector(array(lineArr), trainingWeights)) != int(currLine[10]):
            #如果预测错误，错误数加1
            errorCount += 1
    #计算错误率
    errorRate = (float(errorCount) / numTestVec)
    print('the error rate of this test is : %f' % errorRate)
    return errorRate

最后是一个用于多次调用coicTest()函数，计算错误率的平均值的函数

def multiTest():
    numTests = 10
    errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print('after %d iterations the average error rete is : %f ' % (numTests,errorSum / float(numTests)))

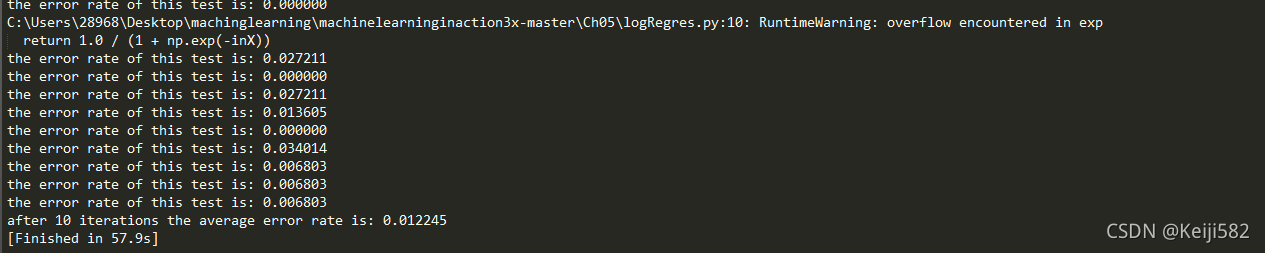
最后实际运行一下代码可以看到结果如下图所示

最终错误率只有0.01左右，当然，调整梯度的步长和训练的迭代次数同样可以改进这个结果，但也会换来时间成本的提升。

源码（基于python3的环境）

import numpy as np

def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))
#改进的随机梯度上升法（随机化）
#使用随机的一个样本来更新回归系数
#numIter迭代
def stoGradAscent1(dataMatrix, classLabels, numIter = 150):
    #m为行 n为列
    m,n = shape(dataMatrix)
    weights = ones(n)
    # 随机梯度, 循环150,观察是否收敛
    for j in range (numIter):
        # [0, 1, 2 .. m-1]
        dataIndex = range(m)
        for i in range(m):
            #alpha会随着迭代次数不断减小，但不会是0
            alpha = 4 / (1.0 + j + i) + 0.0001
            # random.uniform(x, y) 方法将随机生成下一个实数，它在[x,y]范围内,x是这个范围内的最小值，y是这个范围内的最大值。
            randIndex = int(random.uniform(0, len(dataIndex)))
            #随机选取更新
            h = sigmoid(sum(dataMatrix[randIndex] * weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del (list(dataIndex)[randIndex])
    return weights
#输入：特征向量与回归系数
def classifyVector(inX, weights):
    prob = sigmoid(sum(inX * weights))
    #大于0.5 返回 1；否则返回0
    if prob > 0.5:
        return 1.0
    else:
        return 0.0
def colicTest():
    frTrain = open('HorseColicTraining.txt')
    frTest = open('HorseColicTest.txt')
    trainingSet = []
    trainingLabels = []
    # trainingSet 中存储训练数据集的特征，trainingLabels 存储训练数据集的样本对应的分类标签
    for line in frTrain.readlines():
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(10):
            lineArr.append(float(currLine[i]))
        #存入训练样本特征
        trainingSet.append(lineArr)
        #存入训练样本标签
        trainingLabels.append(float(currLine[10]))
    #使用改进后的随机梯度下降算法得到回归系数
    trainingWeights = stoGradAscent1(array(trainingSet), trainingLabels, 500)

    #统计测试集预测错误样本数量和样本总数
    errorCount = 0;
    numTestVec = 0.0
    for line in frTest.readlines():
        #循环一次，样本数加1
        numTestVec += 1.0
        currLine = line.strip().split('\t') #分割
        lineArr = []
        for i in range(10):
            lineArr.append(float(currLine[i]))
        # 利用分类预测函数对该样本进行预测，并与样本标签进行比较
        if int(classifyVector(array(lineArr), trainingWeights)) != int(currLine[10]):
            #如果预测错误，错误数加1
            errorCount += 1
    #计算错误率
    errorRate = (float(errorCount) / numTestVec)
    print('the error rate of this test is : %f' % errorRate)
    return errorRate
if __name__ == "__main__":
    multiTest()