[人工智能]实验三 最小错误率的贝叶斯分类

一. 实验目的

通过学习贝叶斯决策了解统计决策理论中的一个基本方法，对模式识别有个初步的了解，为接下来的学习打下坚实的理论基础。

二. 实验原理

朴素贝叶斯算法

设每个数据样本用一个n维特征向量来描述n个属性的值，即：X={x1，x2，…，xn}，假定有m个类，分别用C1, C2,…，Cm表示。给定一个未知的数据样本X（即没有类标号），若朴素贝叶斯分类法将未知的样本X分配给类Ci，则一定是

P(Ci|X)>P(Cj|X) 1≤j≤m，j≠i

根据贝叶斯定理

由于P(X)对于所有类为常数，最大化后验概率P(Ci|X)可转化为最大化先验概率P(X|Ci)P(Ci)。如果训练数据集有许多属性和元组，计算P(X|Ci)的开销可能非常大，为此，通常假设各属性的取值互相独立，这样

先验概率P(x1|Ci)，P(x2|Ci)，…，P(xn|Ci)可以从训练数据集求得。

根据此方法，对一个未知类别的样本X，可以先分别计算出X属于每一个类别Ci的概率P(X|Ci)P(Ci)，然后选择其中概率最大的类别作为其类别。

朴素贝叶斯算法成立的前提是各属性之间互相独立。当数据集满足这种独立性假设时,分类的准确度较高，否则可能较低。另外，该算法没有分类规则输出。?

TAN算法（树增强型朴素贝叶斯算法）

TAN算法通过发现属性对之间的依赖关系来降低NB中任意属性之间独立的假设。它是在NB网络结构的基础上增加属性对之间的关联(边)来实现的。

实现方法是：用结点表示属性，用有向边表示属性之间的依赖关系，把类别属性作为根结点，其余所有属性都作为它的子节点。通常，用虚线代表NB所需的边，用实线代表新增的边。属性Ai与Aj之间的边意味着属性Ai对类别变量C的影响还取决于属性Aj的取值。

这些增加的边需满足下列条件：类别变量没有双亲结点，每个属性有一个类别变量双亲结点和最多另外一个属性作为其双亲结点。

找到这组关联边之后，就可以计算一组随机变量的联合概率分布如下：

其中ΠAi代表的是Ai的双亲结点。由于在TAN算法中考虑了n个属性中(n-1)个两两属性之间的关联性，该算法对属性之间独立性的假设有了一定程度的降低，但是属性之间可能存在更多其它的关联性仍没有考虑，因此其适用范围仍然受到限制。

三. 实验内容

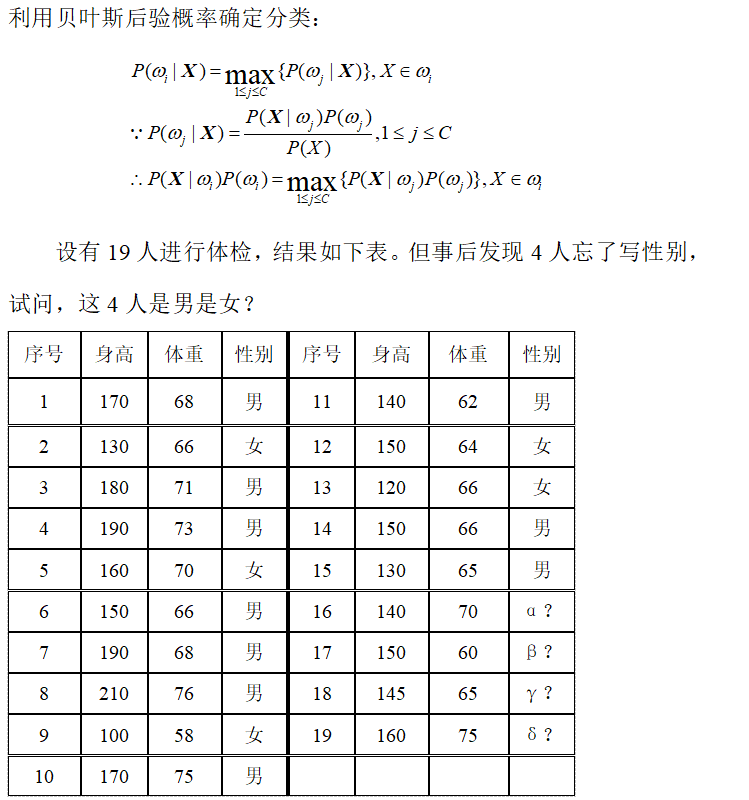
?C=2。男—1类，女—2类。

四. 实验代码

210,76,1;

100,58,2;

170,75,1;

140,62,1;

????????150,64,2;

????????120,66,2;

????????150,66,1;

130,65,1];

?????% 未知类别样本4个

X= ???[140,70,0;

???150,60,0;

???145,65,0;

???160,75,0];

K=4; ?% 未知类别样本个数

pattern ??% 显示pattern

X ????????% 显示未知类别的样本

C=2; % 类别总数C=2

num=zeros(1,C);

%数组 num(i)存放第i类的样本数(i=1...C

for i=1:n % 统计每类样本数

num(pattern(i,3))=num(pattern(i,3))+1;

end

for i=1:C % 输出每类样本数

fprintf('%d 类样本数= %d \n',i,num(i))

end

% 计算每类的先验概率

for i=1:C

??P(i)=num(i)/n;

??% 输出每类的先验概率

??fprintf('%d 类的先验概率=%.2f \n',i,P(i))

end

% float PW1[M],PW2[M]; ?存放后验概率数组

% float height,weight; ?身高-体重

% 对未知类别的样本进行分类判断

for ?k=1:K % 对未知类别样本数据：身高-体重加以处理

???fprintf('第%d 个样本：%d,%d\n',k,X(k,1),X(k,2))

???height=X(k,1);

???weight=X(k,2);

???num1=0;

???for i=1:n

?????if (pattern(i,1)==height&pattern(i,3)==1)

num1=num1+1;

?????end

???end

???if (num1==0) ?% 防止 0 概率，分子分母均作处理：分子加1，分母加类别数或不同取值个数

????PW1(1)=1/(num(1)+2);

????else

????????PW1(1)=(num1+1)/(num(1)+2);

???end

???num1=0;

???for i=1:n

?????if (pattern(i,2)==weight&pattern(i,3)==1)

num1=num1+1;

?????end

???end

???if (num1==0) ?% 防止 0 概率，分子分母均作处理：分子加1，分母加类别数或不同取值个数

????PW1(2)=1/(num(1)+2);

????else

????????PW1(2)=(num1+1)/(num(1)+2);

???end

???num2=0;

???for i=1:n

???if (pattern(i,1)==height&pattern(i,3)==2)

?num2=num2+1;

???????end

???end

???if (num2==0)

??PW2(1)=1/(num(2)+2);

?else

??????PW2(1)=(num2+1)/(num(2)+2);

???end

???num2=0;

???for i=1:n

???if (pattern(i,2)==weight&pattern(i,3)==2)

?num2=num2+1;

???????end

???end

???if (num2==0)

??PW2(2)=1/(num(2)+2);

?else

??????PW2(2)=(num2+1)/(num(2)+2);

???end

???PWT1=PW1(1)*PW1(2)*P(1); % 计算属于第一类的似然概率*先验概率

???PWT2=PW2(1)*PW2(2)*P(2); % 计算属于第二类的似然概率*先验概率

???fprintf(' ??属于第一类的似然概率*先验概率（后验概率*P(X))= %.2f \n',PWT1)

???fprintf(' ??属于第二类的似然概率*先验概率（后验概率*P(X))= %.2f \n',PWT2)

???if (PWT1>PWT2)

???fprintf(' ??%d -th pattern belongs to 1\n',k)

elseif (PWT1<PWT2)

???????fprintf(' ??%d -th pattern belongs to 2\n',k)

?else

???fprintf(' ??%d -th pattern belongs to 1 or 2 is equal\n',k)

?????end

?end