一、实验原理
贝叶斯分类器的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。也就是说,贝叶斯分类器是最小错误率意义上的优化,它遵循“多数占优”这一基本原则。
贝叶斯公式
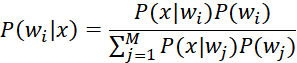
其中,![]() 是先验概率,
是先验概率,![]() 是条件概率,我们要求的
是条件概率,我们要求的![]() 是后验概率。
是后验概率。
由于分母项在不管求样本的哪个后验概率时都是一样的,实际上我们需要关注的只是分子,因此有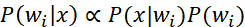 。
。
贝叶斯分类器的分类原理是通过某对象的先验概率,利用贝叶斯公式计算出其后验概率,即该对象属于某一类的概率,选择具有最大后验概率的类作为该对象所属的类。在具有模式的完整统计知识条件下,按照贝叶斯决策理论进行设计的一种最优分类器。分类器是对每一个输入模式赋予一个类别名称的软件或硬件装置,而贝叶斯分类器是各种分类器中分类错误概率最小或者在预先给定代价的情况下平均风险最小的分类器。它的设计方法是一种最基本的统计分类方法。
利用贝叶斯后验概率确定分类:

二、实验内容
设有19人进行体检,结果如下表。但事后发现4人忘了写性别,试问,这4人是男是女?
| 序号 | 身高 | 体重 | 性别 | 序号 | 身高 | 体重 | 性别 |
| 1 | 170 | 68 | 男 | 11 | 140 | 62 | 男 |
| 2 | 130 | 66 | 女 | 12 | 150 | 64 | 女 |
| 3 | 180 | 71 | 男 | 13 | 120 | 66 | 女 |
| 4 | 190 | 73 | 男 | 14 | 150 | 66 | 男 |
| 5 | 160 | 70 | 女 | 15 | 130 | 65 | 男 |
| 6 | 150 | 66 | 男 | 16 | 140 | 70 | α? |
| 7 | 190 | 68 | 男 | 17 | 150 | 60 | β? |
| 8 | 210 | 76 | 男 | 18 | 145 | 65 | γ? |
| 9 | 100 | 58 | 女 | 19 | 160 | 75 | δ? |
| 10 | 170 | 75 | 男 |
C=2。男—1类,女—2类。
三、预习心得
贝叶斯推理实际是借助于新的信息修正先验概率的推理方法。显然,这样的方法如果运用得当,可以在依据概率作出决断时,不必一次收集一个长期过程的大量资料,而可以根据事物发展的情况,不断利用新的信息来修正前面的概率,作出正确决策。例如,当无法对一件事做出准确的判断时,可以通过寻找它的调整因子来增大或者减小它的概率,在经过多次调整后,即可将它的概率增加或者减少到可以做出判断。
四、预习代码
Matlab代码如下:
M=50;% M为最大的类数
% 已知类别样本15个 (身高,体重,类别)。1-男,2-女
n=15;
pattern=[170,68,1;
??????? 130,66,2;
??????? 180,71,1;
??????? 190,73,1;
??????? 160,70,2;
??????? 150,66,1;
??????? 190,68,1;
??????? 210,76,1;
??????? 100,58,2;
??????? 170,75,1;
??????? 140,62,1;
??????? 150,64,2;
??????? 120,66,2;
??????? 150,66,1;
??????? 130,65,1];
???? % 未知类别样本4个
X=??? [140,70,0;
??? ?? 150,60,0;
??? ?? 145,65,0;
??? ?? 160,75,0];
K=4;? % 未知类别样本个数
pattern?? % 显示pattern
X???????? % 显示未知类别的样本
C=2; % 类别总数C=2
num=zeros(1,C);
%数组 num(i)存放第i类的样本数(i=1...C
for i=1:n % 统计每类样本数
??? num(pattern(i,3))=num(pattern(i,3))+1;
end
for i=1:C % 输出每类样本数
??????? fprintf('%d 类样本数= %d \n',i,num(i))
end
% 计算每类的先验概率
for i=1:C
? P(i)=num(i)/n;
? % 输出每类的先验概率
? fprintf('%d 类的先验概率=%.2f \n',i,P(i))
end
% float PW1[M],PW2[M];? 存放后验概率数组
% float height,weight;? 身高-体重
% 对未知类别的样本进行分类判断
for? k=1:K? % 对未知类别样本数据:身高-体重加以处理
?? fprintf('第%d 个样本:%d,%d\n',k,X(k,1),X(k,2))
?? height=X(k,1);
?? weight=X(k,2);
?? num1=0;
?? for i=1:n
???? if (pattern(i,1)==height&pattern(i,3)==1)
??????????? num1=num1+1;
???? end
?? end
?? if (num1==0)? % 防止 0 概率,分子分母均作处理:分子加1,分母加类别数或不同取值个数
??? ??? PW1(1)=1/(num(1)+2);
??? else
??????? PW1(1)=(num1+1)/(num(1)+2);
?? end
?? num1=0;
?? for i=1:n
???? if (pattern(i,2)==weight&pattern(i,3)==1)
??????????? num1=num1+1;
???? end
?? end
?? if (num1==0)? % 防止 0 概率,分子分母均作处理:分子加1,分母加类别数或不同取值个数
??? ??? PW1(2)=1/(num(1)+2);
??? else
??????? PW1(2)=(num1+1)/(num(1)+2);
?? end
?? num2=0;
?? for i=1:n
??? ?? if (pattern(i,1)==height&pattern(i,3)==2)
??????????? ?num2=num2+1;
?????? end
?? end
?? if (num2==0)
??? ? PW2(1)=1/(num(2)+2);
??? ?else
????? PW2(1)=(num2+1)/(num(2)+2);
?? end
?? num2=0;
?? for i=1:n
??? ?? if (pattern(i,2)==weight&pattern(i,3)==2)
??????? ??? ?num2=num2+1;
?????? end
?? end
?? if (num2==0)
??? ? PW2(2)=1/(num(2)+2);
??? ?else
????? PW2(2)=(num2+1)/(num(2)+2);
?? end
?? PWT1=PW1(1)*PW1(2)*P(1); % 计算属于第一类的似然概率*先验概率
?? PWT2=PW2(1)*PW2(2)*P(2); % 计算属于第二类的似然概率*先验概率
?? fprintf('?? 属于第一类的似然概率*先验概率(后验概率*P(X))= %.2f \n',PWT1)
?? fprintf('?? 属于第二类的似然概率*先验概率(后验概率*P(X))= %.2f \n',PWT2)
?? if (PWT1>PWT2)
??? ?? fprintf('?? %d -th pattern belongs to 1\n',k)
??? elseif (PWT1<PWT2)
?????? fprintf('?? %d -th pattern belongs to 2\n',k)
??? ?else
??? ?? fprintf('?? %d -th pattern belongs to 1 or 2 is equal\n',k)
???? end
?end