21.11.22学习内容:(代码均可运行)
首先生成随机数据
#生成随机实验数据
import numpy as np
X=[i for i in range(20)]
X=np.reshape(X,(10,2))#转化为,十个样本,每个样本两个特征值,10*2=20
print('X[:,0]= ',X[:,0])x[:,n]、x[n,:]、x[:,m:n]三者区别如下
'''
X = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11],[12,13,14],[15,16,17],[18,19,20]])
x[:,n]表示在全部数组(维)中取第n个数据,直观来说,x[:,n]就是取所有集合的第n个数据,
x[n,:]表示在n个数组(维)中取全部数据,直观来说,x[n,:]就是取第n集合的所有数据,
x[:,m:n],即取所有数据集的第m到n-1列数据
print(x[n,:])
'''?建立基础线性模型,y=ax+b
#矩阵乘法,例如np.dot(X,X.T)
y=np.dot(X,[3,4])+2
print('y= ',y)运行结果:
X[:,0]= [ 0 2 4 6 8 10 12 14 16 18]
y= [ 6 20 34 48 62 76 90 104 118 132]这时生成图片可以看到,模型过于简单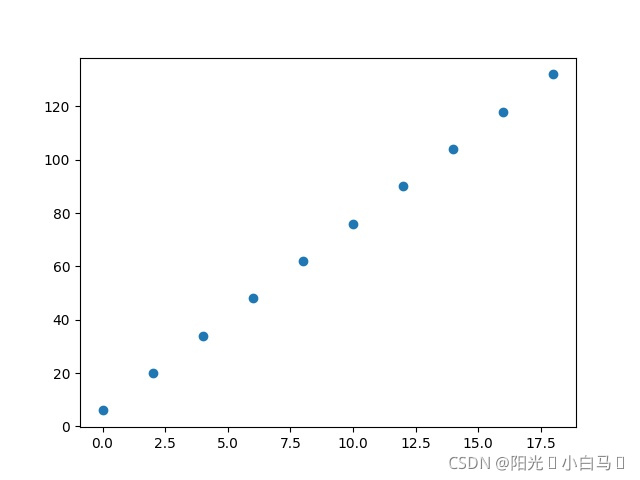
?因此,我们加上随机扰动:
#加入随机扰动
y_random=[]
for i in y:
# np.random.seed(1)
i += np.random.randint(-10, 10)#加入随机-10到10之间的整数作为扰动
y_random.append(i)
print('y_random= ',y_random)
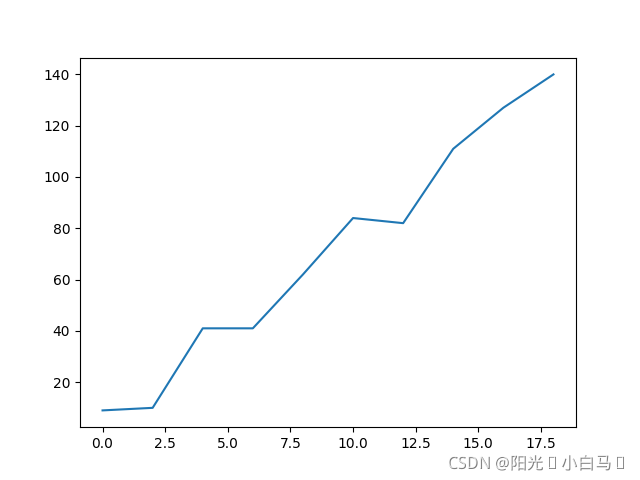
?
?对数据进行预处理,划分训练集以及测试集(若引用,生成的y_random不同,图也不同,不必在意)
#数据预处理
from sklearn.model_selection import train_test_split#数据划分
X_train,X_test,y_train,y_test=train_test_split(X,y_random,shuffle=False,test_size=0.2)
print('X_train= ',X_train)
print('y_test= ',y_test)
from sklearn.preprocessing import StandardScaler#标准化
scaler = StandardScaler()
scaler.fit(X_train)
scaler.transform(X_train)
X_train= [[ 0 1]
[ 2 3]
[ 4 5]
[ 6 7]
[ 8 9]
[10 11]
[12 13]
[14 15]]
y_test= [127, 140]?随意加入空值:可以看到,在3处和末尾分别插入空值。
'''
axis=0代表往跨行(down),而axis=1代表跨列(across)
'''
x_c=np.copy(X)
x_c=np.append(x_c,[[20,np.nan]],axis=0)
x_c=np.insert(x_c,3,[[np.nan,5]],axis=0)
print(x_c)
[[ 0. 1.]
[ 2. 3.]
[ 4. 5.]
[nan 5.]
[ 6. 7.]
[ 8. 9.]
[10. 11.]
[12. 13.]
[14. 15.]
[16. 17.]
[18. 19.]
[20. nan]]空值处理:
1.利用pd.dataframe处理。
-
data=data.fillna
-
data=data.interpolate()
-
data=data.dropna()
#利用pd填补空值
import pandas as pd
data=pd.DataFrame(x_c)
'''
data=data.fillna(method='ffill')
method='ffill',ffill用上一个值填补空值,bfill用后一个值填补空值
data=data.interpolate()
用上下相邻两个值平均值填补
暴力操作:data=data.dropna()直接删除带有空值的行
'''
#data=data.fillna(method='ffill')
data=data.interpolate()
# data=data.dropna()
print(data)2.利用sklearn处理:
SimpleImputer(),用均值填充。
#利用sklearn填补空值
from sklearn.impute import SimpleImputer#导入模块
imp=SimpleImputer()
imp.fit(x_c)
imp=imp.transform(x_c)
x_c=imp
print(x_c)
[[ 0. 1. ]
[ 2. 3. ]
[ 4. 5. ]
[10. 5. ]
[ 6. 7. ]
[ 8. 9. ]
[10. 11. ]
[12. 13. ]
[14. 15. ]
[16. 17. ]
[18. 19. ]
[20. 9.54545455]]线性回归模型构建:
#线性回归模型构建、拟合及使用
from sklearn.linear_model import LinearRegression
model=LinearRegression()
model.fit(X_train,y_train)
model.score(X_test,y_test)#模型评估值
model.predict(X_test)#预测值
model.coef_#斜率
model.intercept_#截距
'''
线性模型:y=X*a+b
model.coef_=[3.70833333 3.70833333]
np.dot(x_test,model.coef_+model.intercept_)
手动计算和LinearRegression()是一样的
'''