特质波动率
“特质波动率之谜”的介绍
风险与收益一直是金融学中形影不离的两个概念。经典的CAPM模型,只考虑了系统性风险,认为股票预期收益率只与市场风险溢价有关。直到1972年,Jensen,Black和Scholes对传统金融学理论提出了不同的看法,认为非系统性风险与股票收益率是存在一定的相关关系,并首次提出了特质波动率的概念。Merton曾从供需的角度来解释这两者之间的关系,认为投资者会对系统风险和非系统风险都要求进行一定的风险补偿,而这一解释也被大家广泛地接受与认可。
一般来讲,我们都认为风险与收益应该是正相关,即风险越高,收益率越高。但在2006年,Ang等人却得出了不一样的结论,他们借助Fama-French三因子模型却发现特质波动率与预期收益率之间的关系变为负相关关系。目前尚未有公认的理论可以解释这种异象,因此引起了剧烈的争论,而这一异象也被称为“特质波动率之谜”。
特质波动率的度量方法
在特质波动率的度量方面,我利用Fama-French三因子模型进行计算
(有关三因子模型的介绍与代码在之前的文章有所讲解,读者们可见文末链接)
首先,通过三因子模型,得到每日的残差,即ε

然后,计算残差的波动率,即当月残差标准差乘以当月总交易天数。

这样就得到我们所要的特质波动率了。
Python代码
Python实现的过程中,我们只需要使用pandas、statsmodels.formula.api两个包即可完成:
import pandas as pd
import statsmodels.formula.api as smf
首先,读取数据,我从锐思数据库中,下载了创业板中2015-2019年所有股票每日收益率、无风险收益率以及创业板每日的三因子:
Factors = pd.read_excel("F:\\公众号\\图文素材\\特质波动率\\Data.xlsx", sheetname = 0, header = 0)
Return = pd.read_excel("F:\\公众号\\图文素材\\特质波动率\\Data.xlsx", sheetname = 1, header = 0)
NoRisk = pd.read_excel("F:\\公众号\\图文素材\\特质波动率\\Data.xlsx", sheetname = 2, header = 0)
为了后续筛选日期方便,我们需要将“日期”的数据类型更改为日期型:
Factors['Date'] = pd.to_datetime(Factors['Date'])
Return['Date'] = pd.to_datetime(Return['Date'])
NoRisk['Date'] = pd.to_datetime(NoRisk['Date'])
通过pd.merge()将数据进行合并:
Data = pd.merge(pd.merge(Factors, Return, on = 'Date'), NoRisk, on = 'Date')
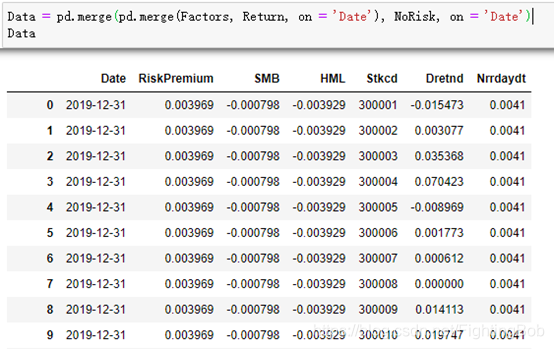
参数说明:
pd.merge(left, right, how=‘inner’, on=None, left_on=None, right_on=None,
left_index=False, right_index=False, sort=True,
suffixes=(’_x’, ‘_y’), copy=True, indicator=False,
validate=None)
1、left: 拼接的左侧DataFrame对象
2、right: 拼接的右侧DataFrame对象
3、on: 要加入的列或索引级别名称。 必须在左侧和右侧DataFrame对象中找到。 如果未传递且left_index和right_index为False,则DataFrame中的列的交集将被推断为连接键。
4、left_on:左侧DataFrame中的列或索引级别用作键。 可以是列名,索引级名称,也可以是长度等于DataFrame长度的数组。
5、right_on: 左侧DataFrame中的列或索引级别用作键。 可以是列名,索引级名称,也可以是长度等于DataFrame长度的数组。
6、left_index: 如果为True,则使用左侧DataFrame中的索引(行标签)作为其连接键。 对于具有MultiIndex(分层)的DataFrame,级别数必须与右侧DataFrame中的连接键数相匹配。
7、right_index: 与left_index功能相似。
8、how: One of ‘left’, ‘right’, ‘outer’, ‘inner’. 默认inner。inner是取交集,outer取并集。比如left:[‘A’,‘B’,‘C’];right[’'A,‘C’,‘D’];inner取交集的话,left中出现的A会和right中出现的买一个A进行匹配拼接,如果没有是B,在right中没有匹配到,则会丢失。'outer’取并集,出现的A会进行一一匹配,没有同时出现的会将缺失的部分添加缺失值。
9、sort: 按字典顺序通过连接键对结果DataFrame进行排序。 默认为True,设置为False将在很多情况下显着提高性能。
10、suffixes: 用于重叠列的字符串后缀元组。 默认为(‘x’,’ y’)。
11、copy: 始终从传递的DataFrame对象复制数据(默认为True),即使不需要重建索引也是如此。
12、indicator: 将一列添加到名为_merge的输出DataFrame,其中包含有关每行源的信息。 _merge是分类类型,并且对于其合并键仅出现在“左”DataFrame中的观察值,取得值为left_only,对于其合并键仅出现在“右”DataFrame中的观察值为right_only,并且如果在两者中都找到观察点的合并键,则为left_only。
然后从日期中提取年份和月份:
Data[‘Year’] = Data[‘Date’].dt.year
Data[‘Month’] = Data[‘Date’].dt.month
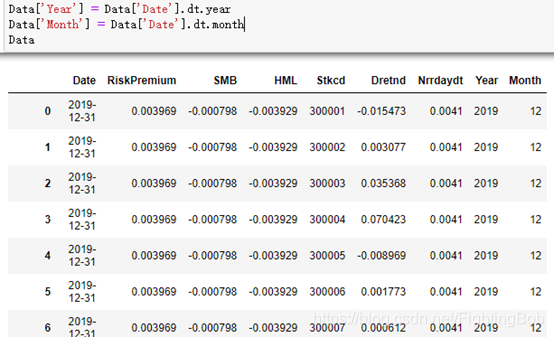
我们创建一个函数,用于提取某只股票某月下的数据:
def get_month_data(data, code, year, month):
month_data = data[(data.Stkcd == code) & (data.Year == year) & (data.Month == month)]
return month_data
接下来,我们计算一下300001这只股票在2019年12月份的特质波动率。
首先,我们获得这只股票当月的数据:
example = get_month_data(Data, 300001, 2019, 12)
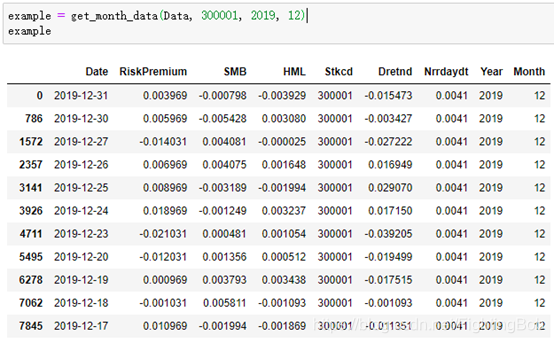
统计当月交易总天数:
N = len(example)

建立回归模型,并计算残差:
model = smf.ols('Dretnd - Nrrdaydt ~ RiskPremium + SMB + HML', data = example).fit()
predict = model.params['Intercept'] + model.params['RiskPremium']*example['RiskPremium'] + model.params['SMB']*example['SMB'] + model.params['HML']*example['HML']
residual = example['Dretnd'] – predict
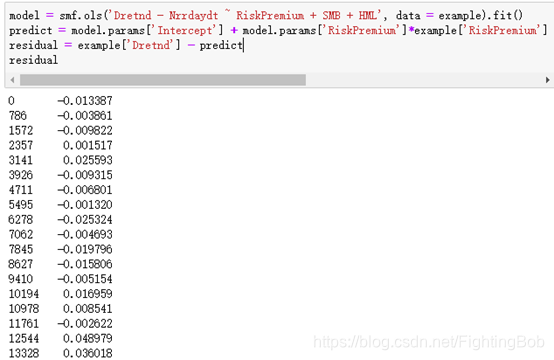
接着,计算得出特质波动率:
IV = residual.std(ddof=1) * N

参数说明:
pd.std(ddof = 1)
该函数是pandas所带的标准差计算方法,默认按照无偏估计进行计算,即ddof = 1,即n-ddof。
最后,我们可以用循环语句进行遍历计算,并创建一个DataFrame进行储存和导出:
