[人工智能]图像识别-MNIST分类问题

摘要

本报告基于美国国家标准与技术研究院收集整理的MNIST手写数字数据集。在当前时代背景下，仍有大量手写数字需要处理，对它们的识别及分类是解决问题的关键。对此，本论文中练习并体会了MNIST数据集中手写数据的分类。论文主要内容包括：实验过程的记录，实验结果的简要分析，相关方法的介绍。实验过程由Python实现，使用了AutoEncoder降维方法及MLP、FCN分类方法，通过比较两种分类方法的准确率得到最终结论。

关键词:手写数字识别；超高维数据；数据分类

ABSTRACT

This report is based on MNIST handwritten digital data set collected by National Institute of Standards and Technology, NIST. In the current era, there are still a large number of handwritten digits to be processed, and their recognition and classification is the key to solve the problem. In this paper, I practice and experience the classification of handwritten data in MNIST data set. The main contents of this paper include: the recording of the experimental process, the brief analysis of the experimental results, and the introduction of the relevant methods. The experimental process is implemented by Python 3. The AutoEncoder, Multilayer Perceptron and Fully Convolutional Networks are used. The final conclusion is obtained by comparing the accuracy of the two classification methods.

Key words：Handwritten digit recognition, Ultra-high dimensional data, Data Classification

1 研究背景及意义

1.1 研究背景
1.1.1 起源
美国国家标准与技术研究院有识别手写数字的需求，因此收集统计了来自二百余位民众的手写数字样式，将其字迹图像整理为MNIST数据集，用算法实现对手写数字的识别；同时，MNIST数据集也起到了帮助研究者评测理解机器学习算法的作用。

1.1.2 发展
1998年，LeCun在其论文《Gradient-Based Learning Applied to Document Recognition》中用CNN算法实现了基于MNIST数据集的手写数字识别。
MNIST逐渐成为广为人知的手写数字数据集，被越来越多的人广泛使用，相关项目成为被学习的经典示例。

1.2 研究意义
体会MNIST数据集，练习相关方法的使用；在Python中实现基于MNIST数据集的手写数字识别，并依据实验结果进一步确定更优方法。

2 数据来源

2.1 MNIST数据集
2.1.1 数据集介绍
MNIST数据集是美国国国家标准与技术研究院整理的大型手写数字数据集，其中包含训练集60000个，测试集10000个。数字图像已经经过处理，每个图像文件大小统一，为28*28像素，包含数字0-9中的一个；且图像中手写数字居中显示，便于操作及处理。

2.1.2 数据集官网
MNIST官网为： http://yann.lecun.com/exdb/mnist/index.html ，可从中获取需要的数据。

3 实证分析

3.1 数据预处理及降维
3.1.1 准备工作
解压下载好的mnist.zip文件，共包含1个npz文件及4个gz文件。其中gz文件存储的是向量及多维度矩阵，含有手写数字的图像及标签；npz文件起到一定整合作用，后续编写Python代码时仅读取npz文件即可获取数据集中需要使用的内容。

import tensorflow
import keras
import matplotlib.pyplot as plt
import numpy as np

#原始数据中涉及到的文件均已上传到jupyter notebook
#打开npz文件
mnist = np.load('mnist.npz')

tensorlow是机器学习领域常用的深度学习框架，可用于实现构建神经网络分布式学习和交互系统等，具有通用性强、可移植性强等特点，在手写识别、图像分类等应用中展现良好效果。
keras是一个人工神经网络库，可用于深度学习模型的各项操作，在Python中以tensorflow为基础进行安装及导入。
在Python3中初次使用tensorflow及keras需要使用pip install的方法进行安装，此处已经预先安装好，故省略。

3.1.2 设置训练集及测试集

#设置train及test
x_train = mnist['x_train']
y_train = mnist['y_train']
x_test = mnist['x_test']
y_test = mnist['y_test']

在进行机器学习的过程中，需要将数据分割为训练集及测试集两部分，用训练集的数据训练模型，在测试集验证模型效果。

mnist数据集中已经预先分割好，只需要分别设置在x和y两个方向上的训练集及测试集即可。同时还可以预览设置好的训练集及测试集。

3.1.3 预览数据

#预览一个图像
plt.figure(figsize=(5,5))
plt.imshow(x_train[300])

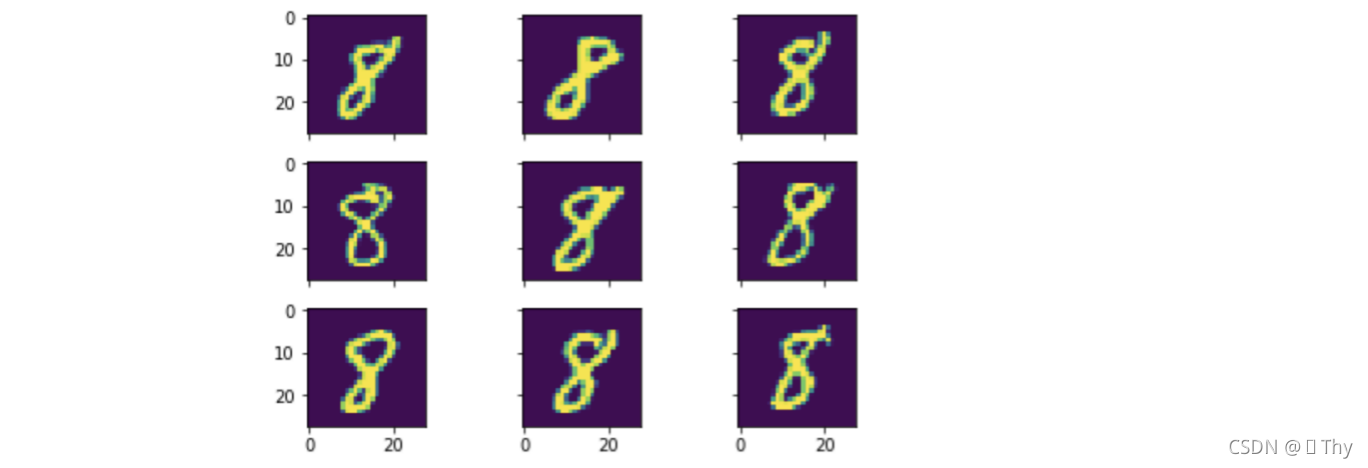
在执行后续操作前，对mnist数据中的原始手写数字图像进行预览，便于对数据集的理解。此处采用两种预览方式，查看了数据中的单个数字8，以及同时查看多个数字8。根据mnist数据集的特点，每个图像包含的字迹均不同。

#还可以一次预览多个图像，我们可以看到这些手写的数字，每个长得都不一样
fig, ax = plt.subplots(
    nrows=3,
    ncols=3,
    sharex=True,
    sharey=True, )
ax = ax.flatten()
for i in range(9):
    img = x_train[y_train == 8][i]
    ax[i].imshow(img,interpolation='nearest')
plt.tight_layout()
plt.show()

3.1.4 查看形状
使用shape分别查看训练集及测试集每维的大小。训练集中共包含60000个图像，测试集中包含10000个图像，每个图像为28*28像素的形式。

3.1.5 归一化
将图像数据归一化，起到简化计算的效果。此处需要将原本的[0,255]转换为[0,1]，对训练集及测试集直接做除法即可实现。

#将图像数据归一化
#原本为[0,255]，转换为[0,1]
x_train = x_train / 255
x_test = x_test / 255

3.1.6 向量化
在上述3.1.4中判断出数据中的图像为28*28像素，为了后续操作的正常执行，需要将每个图像转换为维度是784的向量。

#由上知，每个图像为28x28，将其全部转换为784的向量
x_train = x_train.reshape(60000, 784)
x_test = x_test.reshape(10000, 784)

转换后：已变为向量，而非图像

3.1.7 降维
使用AutoEncoder进行降维，关于AutoEncoder的机制已经在2.3中有所了解。为了便于获得较好的可视化效果，这里将epochs设置为50，将数据降到两维。

#降维
x_train = x_train.reshape(x_train.shape[0], -1)
x_test = x_test.reshape(x_test.shape[0], -1)
encoding_dim = 2
 
encoder = keras.models.Sequential([
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(32, activation='relu'),
    keras.layers.Dense(8, activation='relu'),
    keras.layers.Dense(encoding_dim)])
 
decoder = keras.models.Sequential([
    keras.layers.Dense(8, activation='relu'),
    keras.layers.Dense(32, activation='relu'),
    keras.layers.Dense(128, activation='relu'),
    keras.layers.Dense(784, activation='tanh')])
 
AutoEncoder = keras.models.Sequential([encoder,decoder])
AutoEncoder.compile(optimizer='adam', loss='mse')
AutoEncoder.fit(x_train, x_train, epochs=50, batch_size=256)
 
predict = encoder.predict(x_test)

输出降维后的图像。

plt.scatter(predict[:, 0], predict[:, 1], c=y_test)
plt.show()

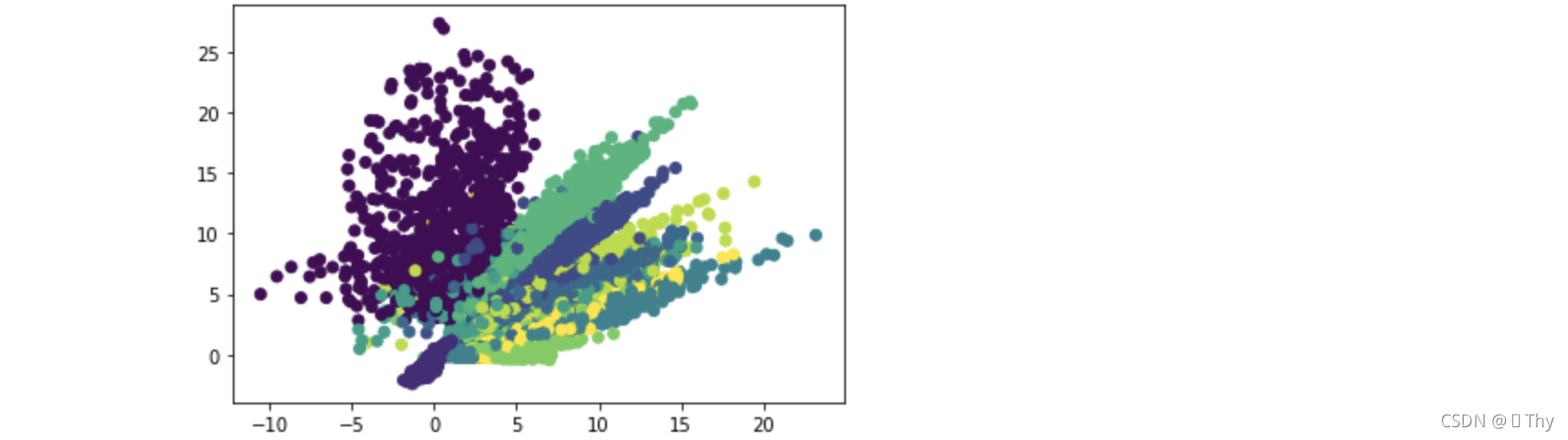
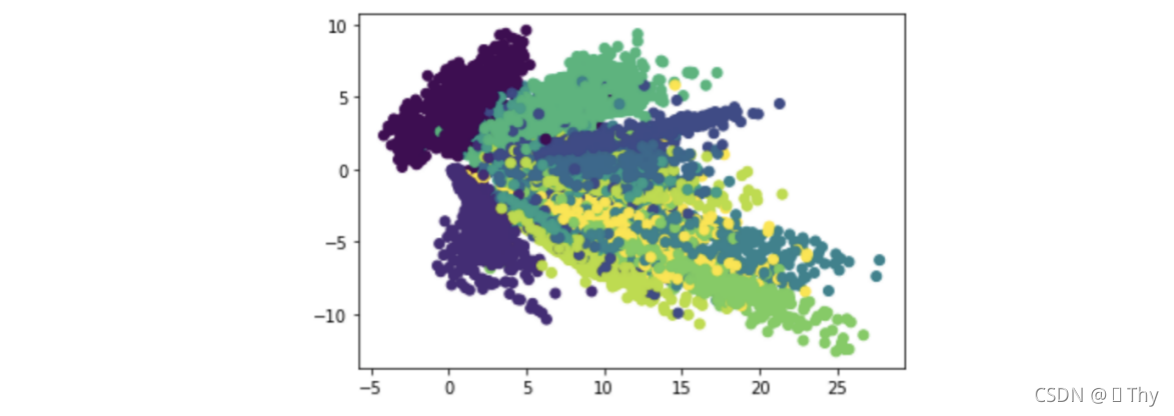
另外，重新执行AutoEncoder降维，图像会有变化。例如：

3.2 使用MLP分类
3.2.1 构建模型
这里想要运用MLP多层感知器对MNIST数据集实现分类。

其中，Sequential是keras中的序贯模型，具有线性结构顺序。Activation、Dense、Dropout是keras的常用网络层。Activation的效果是给一个层赋予激活函数；Dense为全连接层，可实现连接上一层得到非线性组合；Dropout作用于输入数据，会随机断开部分输入，防止过拟合。

from keras.models import Sequential
from keras.layers import Activation,Dense,Dropout

运用上述组件构建包含Softmax函数的分类模型。

model = Sequential()
model.add(Dense(512, input_shape=(784,)))
model.add(Activation('relu')) 
model.add(Dropout(0.2))  
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(10))
model.add(Activation('softmax')) 

3.2.2 训练模型
将训练集套用在构建好的模型中。经过几次尝试发现电脑性能有限，迭代次数不宜过多，且准确率受影响不大，所以暂时将epochs设为10。

model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['accuracy'])

model.fit(x_train, y_train,
          batch_size=16, epochs=25,verbose=0,
          validation_data=(x_test, y_test))

3.2.3 评估模型
将测试集套用在模型中，并计算准确率。在epochs=10时算得准确率为98.33%。

score = model.evaluate(x_test, y_test, verbose=0)
print('准确率为：', score[1])

还可以修改3.2.2中的迭代次数，将epochs提高为25，再次测试。
发现相较于epochs=10时准确率差异不大，甚至反而降低了一些。推测这是因为迭代次数还不够多，准确率有一定波动。

3.3 使用FCN分类
3.3.1 构建模型
这里使用FCN对MNIST数据集实现分类。首先构建模型，为了和上面的MLP方法有所区分，所以在FCN构建时把相关的变量命名为model2、score2。在构建FCN模型时同样要使用到keras的序贯模型Sequential及常用网络层Dense、Activation等。

在代码方面，FCN和MLP最大的区别在于：MLP的Activation层使用的激活函数是relu，而FCN的Activation层使用的则是tanh。

构建FCN模型过程如下：

model2 = Sequential()
model2.add(Dense(784, input_dim=784, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(512, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(512, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(10, kernel_initializer='normal', 
                 activation= 'softmax'))

3.2.2 训练模型
套用训练集，经尝试后发现迭代速度较MLP方法要快很多，因此这里将epochs取为较大的100，希望取得更高一些的准确率。

model2.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

model2.fit(x_train, y_train, epochs=100, batch_size=200, verbose=1, 
            validation_data=(x_test,y_test))

3.2.3 评估模型
套用测试集，得到准确率为98.35%，在数值上较为可观。

score2 = model2.evaluate(x_test,y_test, verbose=0)
print('准确率为:',score2[1])

4 结论

本文使用MNIST数据集进行实验，全程采用Python3编写代码。在预处理部分运用归一化等手段，使用AutoEncoder自动编码器对数据压缩降维，此外还采用MLP及FCN两种方法对数据进行分类。

观察实验过程中MLP及FCN运行后的准确率，前者为98.19%，后者为98.35%，FCN在数值上略高一些。

但是这样的比较是存在问题的，这是因为在实验中使用两种方法时分别迭代了不同次数。

因此再补充一种epochs均为100的实验，起到尽量控制变量的效果。

#MLP
model = Sequential()
model.add(Dense(512, input_shape=(784,)))
model.add(Activation('relu')) 
model.add(Dropout(0.2))  
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(10))
model.add(Activation('softmax')) 
model.compile(optimizer='adam',loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train,
          batch_size=16, epochs=100,verbose=0,
          validation_data=(x_test, y_test))
score = model.evaluate(x_test, y_test, verbose=0)
print('MLP补充实验准确率为：', score[1])

#FCN
model2 = Sequential()
model2.add(Dense(784, input_dim=784, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(512, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(512, kernel_initializer='normal', 
                 activation= 'tanh'))
model2.add(Dense(10, kernel_initializer='normal', 
                 activation= 'softmax'))
model2.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model2.fit(x_train, y_train, epochs=100, batch_size=200, verbose=1, 
            validation_data=(x_test,y_test))
score2 = model2.evaluate(x_test,y_test, verbose=0)
print('FCN补充实验准确率为:',score2[1])

结果为：MLP补充实验准确率为98.53%，FCN补充实验准确率为98.34%。

因此，采用MLP方法分类的准确率相较于采用FCN方法较高一些。