关于书中的卡尔曼滤波感觉特别难,看不懂到底在说些什么,只知道在SLAM中用的比较多,具体讲的通俗点的可以看下面的博客,但是感觉还是很难懂。
一:点云查看工具安装:
CloudCompare安装:
方法1:
命令行安装:
sudo snap install cloudcompare安装完成后,可以将 ccViewer和CloudCompare添加到任务栏里,也可以使用下面的命令行打开:

打开ccViewer:
cloudcompare.ccViewer打开CloudCompare:
cloudcompare.CloudCompare方法2:
在软件中心中进行安装:
MeshLab安装:
方法1:
命令行安装
sudo add-apt-repository ppa:zarquon42/meshlab然后按Enter键,继续
sudo apt-get install meshlab
?方法2:
软件中心安装
bundle_adjustment_ceres.cpp
#include <iostream>
#include <ceres/ceres.h>
#include "common.h"//使用common.h中定义的BALProblem类读入该文件的内容
#include "SnavelyReprojectionError.h"
using namespace std;
void SolveBA(BALProblem &bal_problem);//定义SolveBA函数
int main(int argc, char **argv) {
if (argc != 2) {
cout << "usage: bundle_adjustment_ceres bal_data.txt" << endl;//输出使用方法
return 1;
}
BALProblem bal_problem(argv[1]);
bal_problem.Normalize();//归一化 将所有路标点的中心置零,然后做一个合适尺度的缩放
bal_problem.Perturb(0.1, 0.5, 0.5);//通过Perturb函数给数据加入噪声
bal_problem.WriteToPLYFile("initial.ply");//存储最初点云
SolveBA(bal_problem);//BA求解
bal_problem.WriteToPLYFile("final.ply");//存储最终点云
return 0;
}
void SolveBA(BALProblem &bal_problem) {
const int point_block_size = bal_problem.point_block_size();
const int camera_block_size = bal_problem.camera_block_size();
double *points = bal_problem.mutable_points();
double *cameras = bal_problem.mutable_cameras();
// Observations is 2 * num_observations long array observations
// [u_1, u_2, ... u_n], where each u_i is two dimensional, the x
// and y position of the observation.
const double *observations = bal_problem.observations();
ceres::Problem problem;
for (int i = 0; i < bal_problem.num_observations(); ++i)
{
ceres::CostFunction *cost_function;
// Each Residual block takes a point and a camera as input
// and outputs a 2 dimensional Residual
cost_function = SnavelyReprojectionError::Create(observations[2 * i + 0], observations[2 * i + 1]);//调用SnavelyReprojectionError.h c文件
// If enabled use Huber's loss function.
ceres::LossFunction *loss_function = new ceres::HuberLoss(1.0);
// Each observation corresponds to a pair of a camera and a point
// which are identified by camera_index()[i] and point_index()[i]
// respectively.
double *camera = cameras + camera_block_size * bal_problem.camera_index()[i];
//camera_block_size = bal_problem.camera_block_size();
//*camera = cameras + bal_problem.camera_block_size() * bal_problem.camera_index()[i]
double *point = points + point_block_size * bal_problem.point_index()[i];
//point_block_size = bal_problem.point_block_size();
//*point = points + bal_problem.point_block_size() * bal_problem.point_index()[i]
problem.AddResidualBlock(cost_function, loss_function, camera, point); // 向问题中添加误差项
//CostFunction* : 描述最小二乘的基本形式即代价函数
//LossFunction* : 描述核函数的形式
}
// show some information here ...
std::cout << "bal problem file loaded..." << std::endl;//输出bal problem file loaded...
std::cout << "bal problem have " << bal_problem.num_cameras() << " cameras and "
<< bal_problem.num_points() << " points. " << std::endl;//bal_problem.num_cameras()表示相机位姿个数
//bal_problem.num_points()表示路标点数
std::cout << "Forming " << bal_problem.num_observations() << " observations. " << std::endl;// bal_problem.num_observations()表示观测点数
std::cout << "Solving ceres BA ... " << endl;//BA求解
ceres::Solver::Options options; // 这里有很多配置项可以填Options类嵌入在Solver类中 ,在Options类中可以设置关于求解器的参数
options.linear_solver_type = ceres::LinearSolverType::SPARSE_SCHUR;
// 增量方程如何求解 这里的linear_solver_type 是一个Linear_solver_type的枚举类型的变量
//使用Schur消元
options.minimizer_progress_to_stdout = true;
ceres::Solver::Summary summary;// 优化信息
ceres::Solve(options, &problem, &summary);
std::cout << summary.FullReport() << "\n";
}
CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(bundle_adjustment)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3 -std=c++14")
LIST(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
Find_Package(G2O REQUIRED)
Find_Package(Eigen3 REQUIRED)
Find_Package(Ceres REQUIRED)
Find_Package(Sophus REQUIRED)
Find_Package(CSparse REQUIRED)
SET(G2O_LIBS g2o_csparse_extension g2o_stuff g2o_core cxsparse)
include_directories(${PROJECT_SOURCE_DIR} ${EIGEN3_INCLUDE_DIR} ${CSPARSE_INCLUDE_DIR})
add_library(bal_common common.cpp)
add_executable(bundle_adjustment_g2o bundle_adjustment_g2o.cpp)
add_executable(bundle_adjustment_ceres bundle_adjustment_ceres.cpp)
target_link_libraries(bundle_adjustment_ceres ${CERES_LIBRARIES} bal_common)
target_link_libraries(bundle_adjustment_g2o ${G2O_LIBS} bal_common)执行效果:
./bundle_adjustment_ceres ../problem-16-22106-pre.txt
Header: 16 22106 83718bal problem file loaded...
bal problem have 16 cameras and 22106 points.
Forming 83718 observations.
Solving ceres BA ...
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.842900e+07 0.00e+00 2.04e+06 0.00e+00 0.00e+00 1.00e+04 0 5.78e-02 1.91e-01
1 1.449093e+06 1.70e+07 1.75e+06 2.16e+03 1.84e+00 3.00e+04 1 1.39e-01 3.30e-01
2 5.848543e+04 1.39e+06 1.30e+06 1.55e+03 1.87e+00 9.00e+04 1 1.39e-01 4.69e-01
3 1.581483e+04 4.27e+04 4.98e+05 4.98e+02 1.29e+00 2.70e+05 1 1.37e-01 6.07e-01
4 1.251823e+04 3.30e+03 4.64e+04 9.96e+01 1.11e+00 8.10e+05 1 1.29e-01 7.35e-01
5 1.240936e+04 1.09e+02 9.78e+03 1.33e+01 1.42e+00 2.43e+06 1 1.34e-01 8.70e-01
6 1.237699e+04 3.24e+01 3.91e+03 5.04e+00 1.70e+00 7.29e+06 1 1.35e-01 1.00e+00
7 1.236187e+04 1.51e+01 1.96e+03 3.40e+00 1.75e+00 2.19e+07 1 1.36e-01 1.14e+00
8 1.235405e+04 7.82e+00 1.03e+03 2.40e+00 1.76e+00 6.56e+07 1 1.40e-01 1.28e+00
9 1.234934e+04 4.71e+00 5.04e+02 1.67e+00 1.87e+00 1.97e+08 1 1.34e-01 1.41e+00
10 1.234610e+04 3.24e+00 4.31e+02 1.15e+00 1.88e+00 5.90e+08 1 1.34e-01 1.55e+00
11 1.234386e+04 2.24e+00 3.27e+02 8.44e-01 1.90e+00 1.77e+09 1 1.34e-01 1.68e+00
12 1.234232e+04 1.54e+00 3.44e+02 6.69e-01 1.82e+00 5.31e+09 1 1.35e-01 1.82e+00
13 1.234126e+04 1.07e+00 2.21e+02 5.45e-01 1.91e+00 1.59e+10 1 1.39e-01 1.96e+00
14 1.234047e+04 7.90e-01 1.12e+02 4.84e-01 1.87e+00 4.78e+10 1 1.35e-01 2.09e+00
15 1.233986e+04 6.07e-01 1.02e+02 4.22e-01 1.95e+00 1.43e+11 1 1.39e-01 2.23e+00
16 1.233934e+04 5.22e-01 1.03e+02 3.82e-01 1.97e+00 4.30e+11 1 1.33e-01 2.36e+00
17 1.233891e+04 4.25e-01 1.07e+02 3.46e-01 1.93e+00 1.29e+12 1 1.41e-01 2.50e+00
18 1.233855e+04 3.59e-01 1.04e+02 3.15e-01 1.96e+00 3.87e+12 1 1.34e-01 2.64e+00
19 1.233825e+04 3.06e-01 9.27e+01 2.88e-01 1.98e+00 1.16e+13 1 1.41e-01 2.78e+00
20 1.233799e+04 2.61e-01 1.17e+02 2.16e-01 1.97e+00 3.49e+13 1 1.34e-01 2.91e+00
21 1.233777e+04 2.18e-01 1.22e+02 1.16e-01 1.97e+00 1.05e+14 1 1.38e-01 3.05e+00
22 1.233760e+04 1.73e-01 1.10e+02 9.34e-02 1.89e+00 3.14e+14 1 1.40e-01 3.19e+00
23 1.233746e+04 1.37e-01 1.14e+02 9.06e-02 1.98e+00 9.41e+14 1 1.39e-01 3.33e+00
24 1.233735e+04 1.13e-01 1.18e+02 2.73e-01 1.96e+00 2.82e+15 1 1.40e-01 3.47e+00
WARNING: Logging before InitGoogleLogging() is written to STDERR
W1121 21:50:53.870322 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
25 1.233735e+04 0.00e+00 1.18e+02 0.00e+00 0.00e+00 1.41e+15 1 3.90e-02 3.51e+00
26 1.233725e+04 9.50e-02 1.19e+02 8.90e-01 1.99e+00 4.24e+15 1 1.49e-01 3.66e+00
W1121 21:50:54.052893 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
27 1.233725e+04 0.00e+00 1.19e+02 0.00e+00 0.00e+00 2.12e+15 1 3.33e-02 3.69e+00
28 1.233718e+04 6.92e-02 5.72e+01 2.56e-01 1.70e+00 6.35e+15 1 1.88e-01 3.88e+00
W1121 21:50:54.284538 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
29 1.233718e+04 0.00e+00 5.72e+01 0.00e+00 0.00e+00 3.18e+15 1 4.32e-02 3.92e+00
30 1.233714e+04 3.65e-02 5.84e+01 4.08e-01 1.93e+00 9.53e+15 1 1.87e-01 4.11e+00
W1121 21:50:54.513195 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
31 1.233714e+04 0.00e+00 5.84e+01 0.00e+00 0.00e+00 4.77e+15 1 4.12e-02 4.15e+00
W1121 21:50:54.602217 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
32 1.233714e+04 0.00e+00 5.84e+01 0.00e+00 0.00e+00 1.19e+15 1 8.90e-02 4.24e+00
33 1.233711e+04 3.32e-02 5.96e+01 3.54e-01 2.00e+00 3.57e+15 1 1.50e-01 4.39e+00
W1121 21:50:54.786926 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
34 1.233711e+04 0.00e+00 5.96e+01 0.00e+00 0.00e+00 1.79e+15 1 3.42e-02 4.43e+00
W1121 21:50:54.824539 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
35 1.233711e+04 0.00e+00 5.96e+01 0.00e+00 0.00e+00 4.47e+14 1 3.76e-02 4.46e+00
36 1.233708e+04 3.14e-02 6.13e+01 1.04e-01 2.00e+00 1.34e+15 1 1.88e-01 4.65e+00
37 1.233705e+04 2.50e-02 2.04e+01 6.12e-01 1.68e+00 4.02e+15 1 1.30e-01 4.78e+00
W1121 21:50:55.174543 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
38 1.233705e+04 0.00e+00 2.04e+01 0.00e+00 0.00e+00 2.01e+15 1 3.28e-02 4.81e+00
39 1.233704e+04 1.58e-02 2.04e+01 6.17e-01 1.95e+00 6.03e+15 1 1.49e-01 4.96e+00
W1121 21:50:55.361660 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
40 1.233704e+04 0.00e+00 2.04e+01 0.00e+00 0.00e+00 3.02e+15 1 3.83e-02 5.00e+00
W1121 21:50:55.442020 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
41 1.233704e+04 0.00e+00 2.04e+01 0.00e+00 0.00e+00 7.54e+14 1 8.03e-02 5.08e+00
42 1.233702e+04 1.51e-02 2.06e+01 1.14e-01 2.00e+00 2.26e+15 1 1.87e-01 5.27e+00
W1121 21:50:55.667086 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
43 1.233702e+04 0.00e+00 2.06e+01 0.00e+00 0.00e+00 1.13e+15 1 3.75e-02 5.31e+00
44 1.233701e+04 1.48e-02 2.06e+01 3.49e-01 1.99e+00 3.39e+15 1 1.49e-01 5.46e+00
W1121 21:50:55.853902 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
45 1.233701e+04 0.00e+00 2.06e+01 0.00e+00 0.00e+00 1.70e+15 1 3.80e-02 5.49e+00
46 1.233700e+04 1.42e-02 2.09e+01 5.48e-01 1.99e+00 5.09e+15 1 1.49e-01 5.64e+00
W1121 21:50:56.041224 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
47 1.233700e+04 0.00e+00 2.09e+01 0.00e+00 0.00e+00 2.54e+15 1 3.82e-02 5.68e+00
48 1.233698e+04 1.39e-02 2.17e+01 6.10e-01 2.00e+00 7.63e+15 1 1.49e-01 5.83e+00
W1121 21:50:56.229017 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
49 1.233698e+04 0.00e+00 2.17e+01 0.00e+00 0.00e+00 3.82e+15 1 3.84e-02 5.87e+00
W1121 21:50:56.281327 16417 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
50 1.233698e+04 0.00e+00 2.17e+01 0.00e+00 0.00e+00 9.54e+14 1 5.23e-02 5.92e+00
Solver Summary (v 2.0.0-eigen-(3.4.0)-lapack-suitesparse-(5.7.1)-cxsparse-(3.2.0)-eigensparse-no_openmp)
Original Reduced
Parameter blocks 22122 22122
Parameters 66462 66462
Residual blocks 83718 83718
Residuals 167436 167436
Minimizer TRUST_REGION
Sparse linear algebra library SUITE_SPARSE
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver SPARSE_SCHUR SPARSE_SCHUR
Threads 1 1
Linear solver ordering AUTOMATIC 22106,16
Schur structure 2,3,9 2,3,9
Cost:
Initial 1.842900e+07
Final 1.233698e+04
Change 1.841667e+07
Minimizer iterations 51
Successful steps 36
Unsuccessful steps 15
Time (in seconds):
Preprocessor 0.133346
Residual only evaluation 0.541025 (35)
Jacobian & residual evaluation 2.551966 (36)
Linear solver 2.374793 (50)
Minimizer 5.789036
Postprocessor 0.005307
Total 5.927690
Termination: NO_CONVERGENCE (Maximum number of iterations reached. Number of iterations: 50.)?用MeshLab查看的结果如下:
initial.ply
final.ply
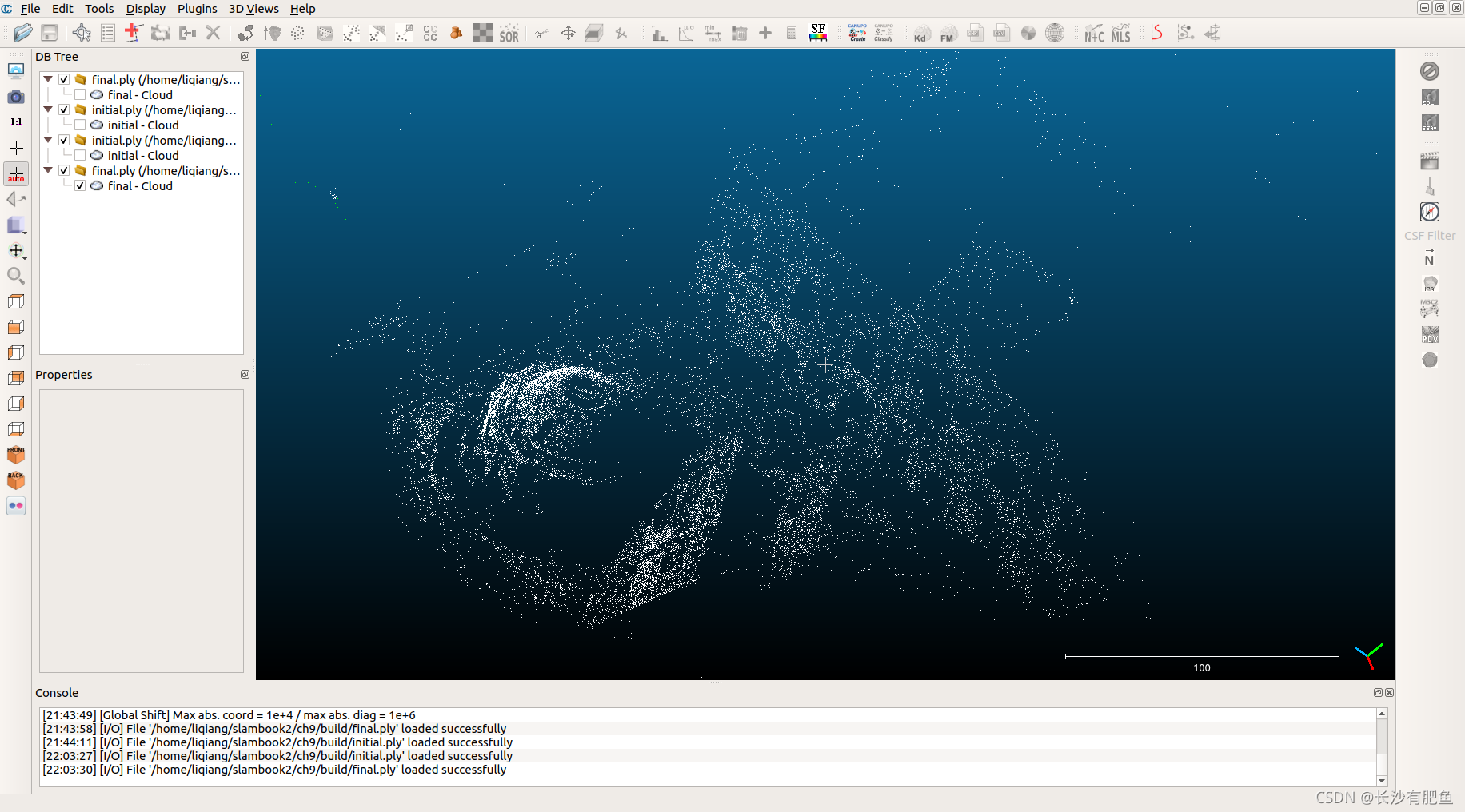
用CloudCompare查看的结果如下:
initial.ply
final.ply
?
bundle_adjustment_g2o.cpp
#include <g2o/core/base_vertex.h>//g2o顶点(Vertex)头文件 视觉slam十四讲p141用顶点表示优化变量,用边表示误差项
#include <g2o/core/base_binary_edge.h>//g2o边(edge)头文件
#include <g2o/core/block_solver.h>//求解器头文件
#include <g2o/core/optimization_algorithm_levenberg.h>//列文伯格——马尔夸特算法头文件
#include <g2o/solvers/csparse/linear_solver_csparse.h>
#include <g2o/core/robust_kernel_impl.h>//鲁棒核函数
#include <iostream>
#include "common.h"//使用common.h中定义的BALProblem类读入该文件的内容
#include "sophus/se3.hpp"
using namespace Sophus;
using namespace Eigen;
using namespace std;
/// 姿态和内参的结构
struct PoseAndIntrinsics {
PoseAndIntrinsics() {}
/// set from given data address
explicit PoseAndIntrinsics(double *data_addr)
{
//每个相机一共有一共有6维的姿态
rotation = SO3d::exp(Vector3d(data_addr[0], data_addr[1], data_addr[2]));//旋转位姿
translation = Vector3d(data_addr[3], data_addr[4], data_addr[5]);//转换矩阵
focal = data_addr[6];//1维焦距
//2维畸变参数
k1 = data_addr[7];
k2 = data_addr[8];
}
/// 将估计值放入内存
void set_to(double *data_addr)
{
auto r = rotation.log();
for (int i = 0; i < 3; ++i) data_addr[i] = r[i];//旋转位姿
for (int i = 0; i < 3; ++i) data_addr[i + 3] = translation[i];//转换矩阵
data_addr[6] = focal;//1维焦距
data_addr[7] = k1;//2维畸变参数
data_addr[8] = k2;//2维畸变参数
}
SO3d rotation;
Vector3d translation = Vector3d::Zero();//置0
double focal = 0;//初始化为0
double k1 = 0, k2 = 0;//将2维畸变参数初始化为0
};
/// 位姿加相机内参的顶点,9维,前三维为so3,接下去为t, f, k1, k2
class VertexPoseAndIntrinsics : public g2o::BaseVertex<9, PoseAndIntrinsics> {
public://以下定义的成员变量和成员函数都是公有的
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;//解决Eigen库数据结构内存对齐问题
VertexPoseAndIntrinsics() {}
// 重置
virtual void setToOriginImpl() override //virtual表示该函数为虚函数,override保留字表示当前函数重写了基类的虚函数
{
_estimate = PoseAndIntrinsics();
}
// 更新
virtual void oplusImpl(const double *update) override {
_estimate.rotation = SO3d::exp(Vector3d(update[0], update[1], update[2])) * _estimate.rotation;
_estimate.translation += Vector3d(update[3], update[4], update[5]);//更新量累加
_estimate.focal += update[6];//1维焦距更新量累加
_estimate.k1 += update[7];//2维畸变参数更新量累加
_estimate.k2 += update[8];//2维畸变参数更新量累加
}
/// 根据估计值投影一个点
Vector2d project(const Vector3d &point)
{
Vector3d pc = _estimate.rotation * point + _estimate.translation;
pc = -pc / pc[2];
double r2 = pc.squaredNorm();
double distortion = 1.0 + r2 * (_estimate.k1 + _estimate.k2 * r2);
return Vector2d(_estimate.focal * distortion * pc[0],
_estimate.focal * distortion * pc[1]);
}
// 存盘和读盘:留空
virtual bool read(istream &in) {} //istream类是c++标准输入流的一个基类
//可参照C++ Primer Plus第六版的6.8节
virtual bool write(ostream &out) const {} //ostream类是c++标准输出流的一个基类
//可参照C++ Primer Plus第六版的6.8节
};
class VertexPoint : public g2o::BaseVertex<3, Vector3d> {
public://以下定义的成员变量和成员函数都是公有的
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;//解决Eigen库数据结构内存对齐问题
VertexPoint() {}
// 重置
virtual void setToOriginImpl() override //virtual表示该函数为虚函数,override保留字表示当前函数重写了基类的虚函数
{
_estimate = Vector3d(0, 0, 0);
}
// 更新
virtual void oplusImpl(const double *update) override
{
_estimate += Vector3d(update[0], update[1], update[2]);//更新量累加
}
// 存盘和读盘:留空
virtual bool read(istream &in) {} //istream类是c++标准输入流的一个基类
//可参照C++ Primer Plus第六版的6.8节
virtual bool write(ostream &out) const {} //ostream类是c++标准输出流的一个基类
//可参照C++ Primer Plus第六版的6.8节
};
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class EdgeProjection :
public g2o::BaseBinaryEdge<2, Vector2d, VertexPoseAndIntrinsics, VertexPoint> {
public://以下定义的成员变量和成员函数都是公有的
EIGEN_MAKE_ALIGNED_OPERATOR_NEW;//解决Eigen库数据结构内存对齐问题
// 计算误差
virtual void computeError() override //virtual表示虚函数,保留字override表示当前函数重写了基类的虚函数
{
auto v0 = (VertexPoseAndIntrinsics *) _vertices[0];
auto v1 = (VertexPoint *) _vertices[1];
auto proj = v0->project(v1->estimate());
_error = proj - _measurement;
}
// use numeric derivatives
virtual bool read(istream &in) {}//istream类是c++标准输入流的一个基类
//可参照C++ Primer Plus第六版的6.8节
virtual bool write(ostream &out) const {}//ostream类是c++标准输出流的一个基类
//可参照C++ Primer Plus第六版的6.8节
};
void SolveBA(BALProblem &bal_problem);//定义SolveBA函数
int main(int argc, char **argv) {
if (argc != 2) {
cout << "usage: bundle_adjustment_g2o bal_data.txt" << endl;//输出使用方法
return 1;
}
BALProblem bal_problem(argv[1]);
bal_problem.Normalize();//归一化 将所有路标点的中心置零,然后做一个合适尺度的缩放
bal_problem.Perturb(0.1, 0.5, 0.5);//通过Perturb函数给数据加入噪声
bal_problem.WriteToPLYFile("initial.ply");//存储最初点云
SolveBA(bal_problem);//BA求解
bal_problem.WriteToPLYFile("final.ply");//存储最终点云
return 0;
}
void SolveBA(BALProblem &bal_problem) {
const int point_block_size = bal_problem.point_block_size();
const int camera_block_size = bal_problem.camera_block_size();
double *points = bal_problem.mutable_points();
double *cameras = bal_problem.mutable_cameras();
// pose dimension 9, landmark is 3
typedef g2o::BlockSolver<g2o::BlockSolverTraits<9, 3>> BlockSolverType;
typedef g2o::LinearSolverCSparse<BlockSolverType::PoseMatrixType> LinearSolverType;
// use LM
auto solver = new g2o::OptimizationAlgorithmLevenberg(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
//c++中的make_unique表示智能指针类型
g2o::SparseOptimizer optimizer;// 图模型
optimizer.setAlgorithm(solver);// 设置求解器
optimizer.setVerbose(true);// 打开调试输出
/// build g2o problem
const double *observations = bal_problem.observations();
// vertex
vector<VertexPoseAndIntrinsics *> vertex_pose_intrinsics;
vector<VertexPoint *> vertex_points;
for (int i = 0; i < bal_problem.num_cameras(); ++i) {
VertexPoseAndIntrinsics *v = new VertexPoseAndIntrinsics();
double *camera = cameras + camera_block_size * i;
v->setId(i);
v->setEstimate(PoseAndIntrinsics(camera));//camera表示优化变量
optimizer.addVertex(v);// 设置连接的顶点
vertex_pose_intrinsics.push_back(v);
}
for (int i = 0; i < bal_problem.num_points(); ++i) {
VertexPoint *v = new VertexPoint();
double *point = points + point_block_size * i;
v->setId(i + bal_problem.num_cameras());
v->setEstimate(Vector3d(point[0], point[1], point[2]));
// g2o在BA中需要手动设置待Marg的顶点
v->setMarginalized(true);
optimizer.addVertex(v);
vertex_points.push_back(v);
}
// edge
for (int i = 0; i < bal_problem.num_observations(); ++i) {
EdgeProjection *edge = new EdgeProjection;
edge->setVertex(0, vertex_pose_intrinsics[bal_problem.camera_index()[i]]);
edge->setVertex(1, vertex_points[bal_problem.point_index()[i]]);
edge->setMeasurement(Vector2d(observations[2 * i + 0], observations[2 * i + 1]));
edge->setInformation(Matrix2d::Identity());//信息矩阵
edge->setRobustKernel(new g2o::RobustKernelHuber());//核函数 鲁棒核函数
optimizer.addEdge(edge);//添加边
}
optimizer.initializeOptimization();
optimizer.optimize(40);//设置迭代次数为40
// set to bal problem
for (int i = 0; i < bal_problem.num_cameras(); ++i) {
double *camera = cameras + camera_block_size * i;
//camera_block_size = bal_problem.camera_block_size();
//*camera = cameras + bal_problem.camera_block_size() * bal_problem.camera_index()[i]
auto vertex = vertex_pose_intrinsics[i];
auto estimate = vertex->estimate();
estimate.set_to(camera);
}
for (int i = 0; i < bal_problem.num_points(); ++i) {
double *point = points + point_block_size * i;
auto vertex = vertex_points[i];
for (int k = 0; k < 3; ++k) point[k] = vertex->estimate()[k];
}
}
CMakeLists.txt
和上面一样
执行结果:
./bundle_adjustment_g2o ../problem-16-22106-pre.txt Header: 16 22106 83718iteration= 0 chi2= 8894423.022949 time= 0.213522 cumTime= 0.213522 edges= 83718 schur= 1 lambda= 227.832660 levenbergIter= 1
iteration= 1 chi2= 1772145.050517 time= 0.187932 cumTime= 0.401455 edges= 83718 schur= 1 lambda= 75.944220 levenbergIter= 1
iteration= 2 chi2= 752585.293391 time= 0.188038 cumTime= 0.589493 edges= 83718 schur= 1 lambda= 25.314740 levenbergIter= 1
iteration= 3 chi2= 402814.243627 time= 0.187588 cumTime= 0.77708 edges= 83718 schur= 1 lambda= 8.438247 levenbergIter= 1
iteration= 4 chi2= 284879.378894 time= 0.188289 cumTime= 0.96537 edges= 83718 schur= 1 lambda= 2.812749 levenbergIter= 1
iteration= 5 chi2= 238356.214415 time= 0.188404 cumTime= 1.15377 edges= 83718 schur= 1 lambda= 0.937583 levenbergIter= 1
iteration= 6 chi2= 193550.755079 time= 0.18828 cumTime= 1.34205 edges= 83718 schur= 1 lambda= 0.312528 levenbergIter= 1
iteration= 7 chi2= 146859.909574 time= 0.188484 cumTime= 1.53054 edges= 83718 schur= 1 lambda= 0.104176 levenbergIter= 1
iteration= 8 chi2= 122887.700218 time= 0.187905 cumTime= 1.71844 edges= 83718 schur= 1 lambda= 0.069451 levenbergIter= 1
iteration= 9 chi2= 97810.139925 time= 0.188426 cumTime= 1.90687 edges= 83718 schur= 1 lambda= 0.046300 levenbergIter= 1
iteration= 10 chi2= 80329.940265 time= 0.18752 cumTime= 2.09439 edges= 83718 schur= 1 lambda= 0.030867 levenbergIter= 1
iteration= 11 chi2= 65663.994405 time= 0.187678 cumTime= 2.28207 edges= 83718 schur= 1 lambda= 0.020578 levenbergIter= 1
iteration= 12 chi2= 55960.726637 time= 0.188224 cumTime= 2.47029 edges= 83718 schur= 1 lambda= 0.013719 levenbergIter= 1
iteration= 13 chi2= 53275.547797 time= 0.187621 cumTime= 2.65791 edges= 83718 schur= 1 lambda= 0.009146 levenbergIter= 1
iteration= 14 chi2= 35983.312124 time= 0.227208 cumTime= 2.88512 edges= 83718 schur= 1 lambda= 0.006097 levenbergIter= 2
iteration= 15 chi2= 32091.891518 time= 0.26721 cumTime= 3.15233 edges= 83718 schur= 1 lambda= 0.016259 levenbergIter= 3
iteration= 16 chi2= 31156.262647 time= 0.227134 cumTime= 3.37947 edges= 83718 schur= 1 lambda= 0.021679 levenbergIter= 2
iteration= 17 chi2= 30773.139623 time= 0.187135 cumTime= 3.5666 edges= 83718 schur= 1 lambda= 0.014453 levenbergIter= 1
iteration= 18 chi2= 29079.563460 time= 0.228139 cumTime= 3.79474 edges= 83718 schur= 1 lambda= 0.012488 levenbergIter= 2
iteration= 19 chi2= 28484.154313 time= 0.227314 cumTime= 4.02205 edges= 83718 schur= 1 lambda= 0.016651 levenbergIter= 2
iteration= 20 chi2= 28445.405201 time= 0.18725 cumTime= 4.2093 edges= 83718 schur= 1 lambda= 0.011101 levenbergIter= 1
iteration= 21 chi2= 27170.592543 time= 0.227542 cumTime= 4.43685 edges= 83718 schur= 1 lambda= 0.011118 levenbergIter= 2
iteration= 22 chi2= 26748.191194 time= 0.2271 cumTime= 4.66395 edges= 83718 schur= 1 lambda= 0.014824 levenbergIter= 2
iteration= 23 chi2= 26675.118188 time= 0.18739 cumTime= 4.85134 edges= 83718 schur= 1 lambda= 0.009883 levenbergIter= 1
iteration= 24 chi2= 26087.985781 time= 0.227215 cumTime= 5.07855 edges= 83718 schur= 1 lambda= 0.010281 levenbergIter= 2
iteration= 25 chi2= 25875.818536 time= 0.227209 cumTime= 5.30576 edges= 83718 schur= 1 lambda= 0.013708 levenbergIter= 2
iteration= 26 chi2= 25831.564925 time= 0.187807 cumTime= 5.49357 edges= 83718 schur= 1 lambda= 0.009139 levenbergIter= 1
iteration= 27 chi2= 25568.344873 time= 0.227318 cumTime= 5.72089 edges= 83718 schur= 1 lambda= 0.011118 levenbergIter= 2
iteration= 28 chi2= 25455.865005 time= 0.227444 cumTime= 5.94833 edges= 83718 schur= 1 lambda= 0.011781 levenbergIter= 2
iteration= 29 chi2= 25454.942053 time= 0.186962 cumTime= 6.13529 edges= 83718 schur= 1 lambda= 0.007854 levenbergIter= 1
iteration= 30 chi2= 25260.709796 time= 0.227445 cumTime= 6.36274 edges= 83718 schur= 1 lambda= 0.009148 levenbergIter= 2
iteration= 31 chi2= 25171.392636 time= 0.227664 cumTime= 6.5904 edges= 83718 schur= 1 lambda= 0.009425 levenbergIter= 2
iteration= 32 chi2= 25104.160294 time= 0.227913 cumTime= 6.81831 edges= 83718 schur= 1 lambda= 0.008637 levenbergIter= 2
iteration= 33 chi2= 25042.986799 time= 0.227786 cumTime= 7.0461 edges= 83718 schur= 1 lambda= 0.008765 levenbergIter= 2
iteration= 34 chi2= 24984.677998 time= 0.227546 cumTime= 7.27365 edges= 83718 schur= 1 lambda= 0.005949 levenbergIter= 2
iteration= 35 chi2= 24943.879912 time= 0.22765 cumTime= 7.5013 edges= 83718 schur= 1 lambda= 0.007933 levenbergIter= 2
iteration= 36 chi2= 24886.075504 time= 0.226954 cumTime= 7.72825 edges= 83718 schur= 1 lambda= 0.005674 levenbergIter= 2
iteration= 37 chi2= 24868.088225 time= 0.227189 cumTime= 7.95544 edges= 83718 schur= 1 lambda= 0.007565 levenbergIter= 2
iteration= 38 chi2= 24833.053138 time= 0.227247 cumTime= 8.18269 edges= 83718 schur= 1 lambda= 0.008448 levenbergIter= 2
iteration= 39 chi2= 24815.047826 time= 0.22722 cumTime= 8.40991 edges= 83718 schur= 1 lambda= 0.009766 levenbergIter= 2
用MeshLab查看的结果如下:
initial.ply
final.ply
用CloudCompare查看的结果如下:
initial.ply
final.ply
课后习题:
1. 证明式(10.25)成立。提示:你可能会用到SMW(Sherman-Morrison-Woodbury)公式,参考[6, 76]。

 ?
?
 ?
?
???转载于:视觉SLAM十四讲(第二版)第9讲习题解答 - 知乎
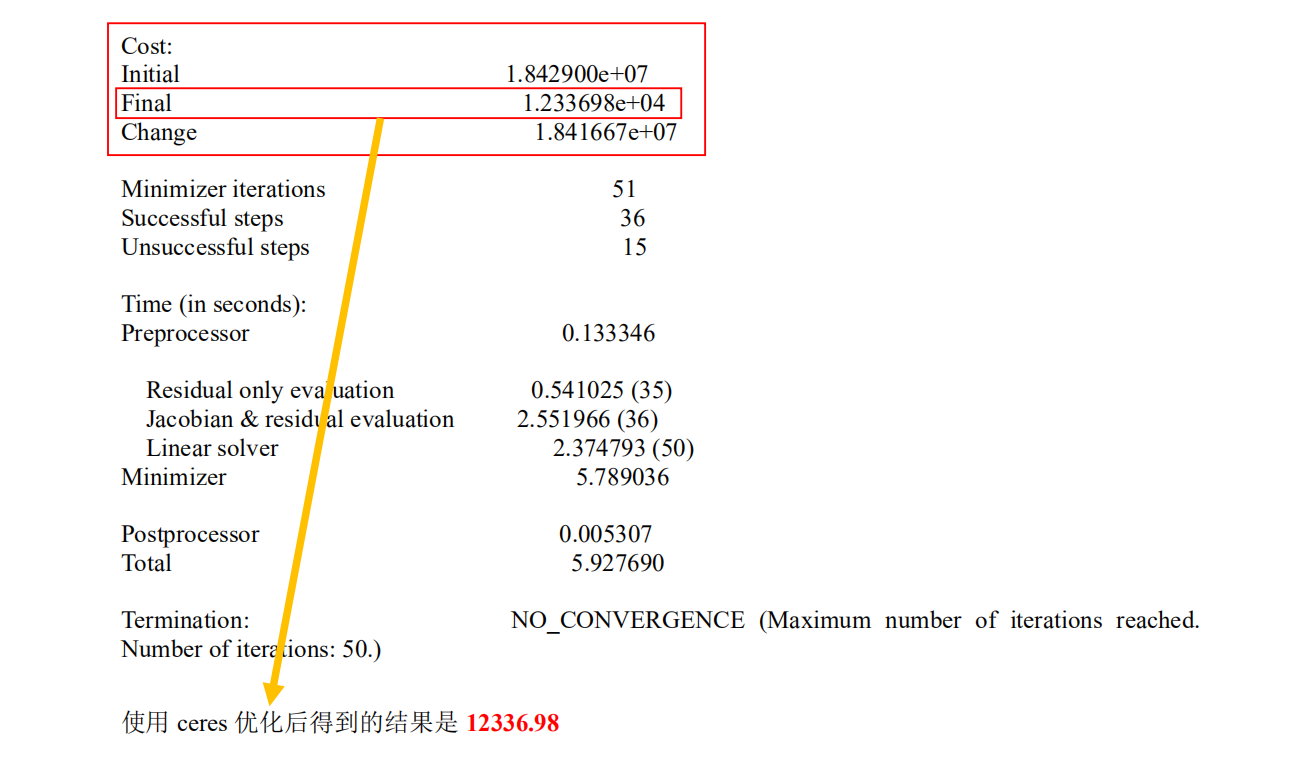
2. 对比g2o 和Ceres 的优化后目标函数的数值。指出为什么两者在Meshlab 中效果一样但为何数值却不同。
?
?

?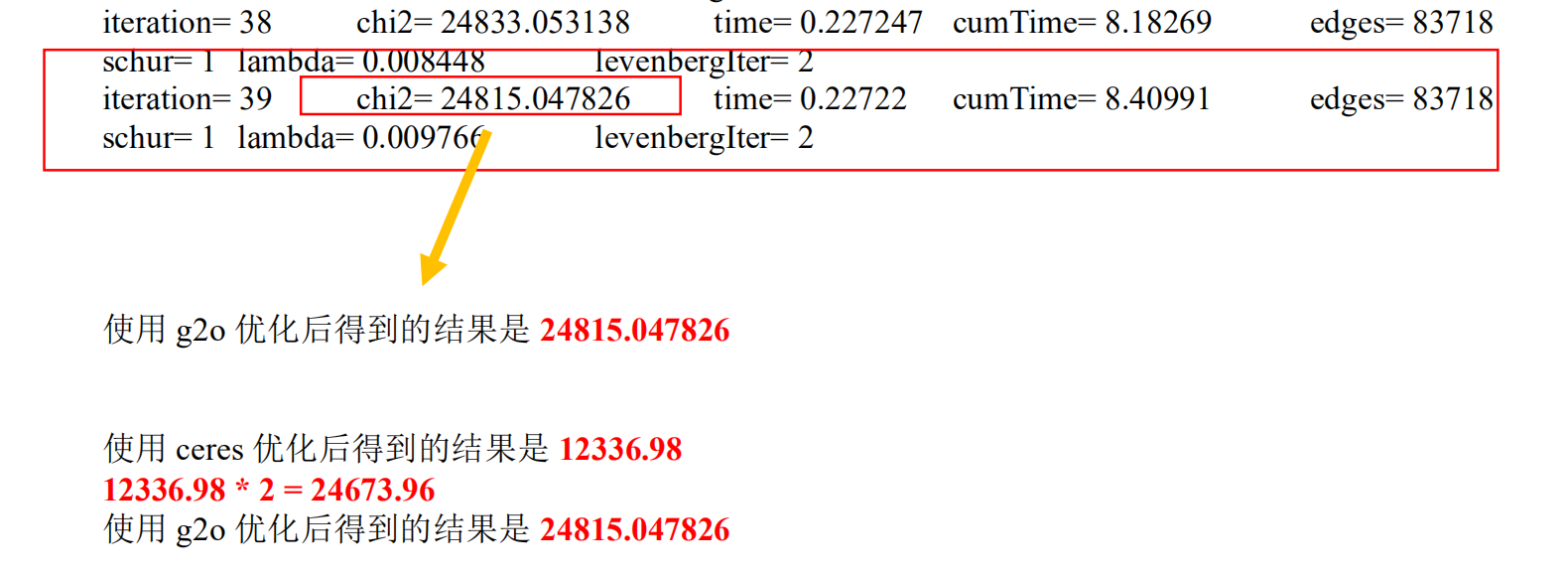
?通过对比两组优化后的值,g2o优化后的数值约为Ceres的两倍左右,原因是原因应该是两个优化库计算目标函数优化后数值的方法不一致(即计算用的范数不同);而不严格为2倍的原因与设置的迭代次数或收敛判断条件不同,出于计算成本的考虑并未做过多的迭代。但是两种优化库优化的目标函数是一致的,范数不同只会影响目标函数的数值,而实际待优化的变量的优化结果是一致的,因此最后得到在点云图像一致。
?转载于:视觉SLAM十四讲(第二版)第9讲习题解答 - 知乎
3. 给Ceres 当中的部分点云进行Schur 消元,看看结果会有什么区别。
3.cpp
#include <iostream>
#include <ceres/ceres.h>
#include "common.h"//使用common.h中定义的BALProblem类读入该文件的内容
#include "SnavelyReprojectionError.h"
using namespace std;
void SolveBA(BALProblem &bal_problem);//定义SolveBA函数
int main(int argc, char **argv) {
if (argc != 2) {
cout << "usage: bundle_adjustment_ceres bal_data.txt" << endl;//输出使用方法
return 1;
}
BALProblem bal_problem(argv[1]);
bal_problem.Normalize();//归一化 将所有路标点的中心置零,然后做一个合适尺度的缩放
bal_problem.Perturb(0.1, 0.5, 0.5);//通过Perturb函数给数据加入噪声
bal_problem.WriteToPLYFile("initial.ply");//存储最初点云
SolveBA(bal_problem);//BA求解
bal_problem.WriteToPLYFile("final_Ceres.ply");//存储最终点云
return 0;
}
void SolveBA(BALProblem &bal_problem) {
const int point_block_size = bal_problem.point_block_size();
const int camera_block_size = bal_problem.camera_block_size();
double *points = bal_problem.mutable_points();
double *cameras = bal_problem.mutable_cameras();
// Observations is 2 * num_observations long array observations
// [u_1, u_2, ... u_n], where each u_i is two dimensional, the x
// and y position of the observation.
const double *observations = bal_problem.observations();
ceres::Problem problem;
for (int i = 0; i < bal_problem.num_observations(); ++i) {
ceres::CostFunction *cost_function;
// Each Residual block takes a point and a camera as input
// and outputs a 2 dimensional Residual
cost_function = SnavelyReprojectionError::Create(observations[2 * i + 0], observations[2 * i + 1]);
// If enabled use Huber's loss function.
ceres::LossFunction *loss_function = new ceres::HuberLoss(1.0);
// Each observation corresponds to a pair of a camera and a point
// which are identified by camera_index()[i] and point_index()[i]
// respectively.
double *camera = cameras + camera_block_size * bal_problem.camera_index()[i];
//camera_block_size = bal_problem.camera_block_size();
//*camera = cameras + bal_problem.camera_block_size() * bal_problem.camera_index()[i]
double *point = points + point_block_size * bal_problem.point_index()[i];
//point_block_size = bal_problem.point_block_size();
//*point = points + bal_problem.point_block_size() * bal_problem.point_index()[i]
problem.AddResidualBlock(cost_function, loss_function, camera, point);// 向问题中添加误差项
//CostFunction* : 描述最小二乘的基本形式即代价函数
//LossFunction* : 描述核函数的形式
}
// show some information here ...
std::cout << "bal problem file loaded..." << std::endl;//输出bal problem file loaded...
std::cout << "bal problem have " << bal_problem.num_cameras() << " cameras and "
<< bal_problem.num_points() << " points. " << std::endl;//bal_problem.num_cameras()表示相机位姿个数
//bal_problem.num_points()表示路标点数
std::cout << "Forming " << bal_problem.num_observations() << " observations. " << std::endl;
std::cout << "Solving ceres BA ... " << endl;//BA求解
ceres::Solver::Options options;// 这里有很多配置项可以填Options类嵌入在Solver类中 ,在Options类中可以设置关于求解器的参数
options.linear_solver_type = ceres::SPARSE_SCHUR; //增量方程如何求解 这里的linear_solver_type 是一个Linear_solver_type的枚举类型的变量
//使用Schur消元
options.minimizer_progress_to_stdout = true;
//SetOrdering
ceres::ParameterBlockOrdering* ordering = new ceres::ParameterBlockOrdering;
// The points come before the cameras
// 增加的部分
for(int i = 0; i < bal_problem.num_points(); ++i)
if(i%2 == 0){
ordering->AddElementToGroup(points + point_block_size * i, 0);
}
else{
ordering->AddElementToGroup(points + point_block_size * i, 1);
}
for(int i = 0; i < bal_problem.num_cameras(); ++i)
ordering->AddElementToGroup(cameras + camera_block_size * i, 1);
options.linear_solver_ordering.reset(ordering);
ceres::Solver::Summary summary;// 优化信息
ceres::Solve(options, &problem, &summary);
std::cout << summary.FullReport() << "\n";
}
CMakeLists.txt
cmake_minimum_required(VERSION 2.8)
project(bundle_adjustment)
set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3 -std=c++14")
LIST(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
Find_Package(G2O REQUIRED)
Find_Package(Eigen3 REQUIRED)
Find_Package(Ceres REQUIRED)
Find_Package(Sophus REQUIRED)
Find_Package(CSparse REQUIRED)
SET(G2O_LIBS g2o_csparse_extension g2o_stuff g2o_core cxsparse)
include_directories(${PROJECT_SOURCE_DIR} ${EIGEN3_INCLUDE_DIR} ${CSPARSE_INCLUDE_DIR})
add_library(bal_common common.cpp)
add_executable(bundle_adjustment_g2o bundle_adjustment_g2o.cpp)
add_executable(bundle_adjustment_ceres bundle_adjustment_ceres.cpp)
add_executable(3 3.cpp)
target_link_libraries(bundle_adjustment_ceres ${CERES_LIBRARIES} bal_common)
target_link_libraries(3 ${CERES_LIBRARIES} bal_common)
target_link_libraries(bundle_adjustment_g2o ${G2O_LIBS} bal_common)执行结果:
./3 ../problem-16-22106-pre.txt Header: 16 22106 83718bal problem file loaded...
bal problem have 16 cameras and 22106 points.
Forming 83718 observations.
Solving ceres BA ...
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.842900e+07 0.00e+00 2.04e+06 0.00e+00 0.00e+00 1.00e+04 0 6.00e-02 1.28e-01
1 1.449093e+06 1.70e+07 1.75e+06 2.16e+03 1.84e+00 3.00e+04 1 4.08e-01 5.36e-01
2 5.848543e+04 1.39e+06 1.30e+06 1.55e+03 1.87e+00 9.00e+04 1 2.15e+00 2.69e+00
3 1.581483e+04 4.27e+04 4.98e+05 4.98e+02 1.29e+00 2.70e+05 1 3.21e-01 3.01e+00
4 1.251823e+04 3.30e+03 4.64e+04 9.96e+01 1.11e+00 8.10e+05 1 7.72e-01 3.78e+00
5 1.240936e+04 1.09e+02 9.78e+03 1.33e+01 1.42e+00 2.43e+06 1 7.96e-01 4.58e+00
6 1.237699e+04 3.24e+01 3.91e+03 5.04e+00 1.70e+00 7.29e+06 1 3.24e-01 4.90e+00
7 1.236187e+04 1.51e+01 1.96e+03 3.40e+00 1.75e+00 2.19e+07 1 1.01e+00 5.91e+00
8 1.235405e+04 7.82e+00 1.03e+03 2.40e+00 1.76e+00 6.56e+07 1 6.00e-01 6.51e+00
9 1.234934e+04 4.71e+00 5.04e+02 1.67e+00 1.87e+00 1.97e+08 1 8.31e-01 7.34e+00
10 1.234610e+04 3.24e+00 4.31e+02 1.15e+00 1.88e+00 5.90e+08 1 3.16e-01 7.66e+00
11 1.234386e+04 2.24e+00 3.27e+02 8.44e-01 1.90e+00 1.77e+09 1 6.69e-01 8.33e+00
12 1.234232e+04 1.54e+00 3.44e+02 6.69e-01 1.82e+00 5.31e+09 1 7.12e-01 9.04e+00
13 1.234126e+04 1.07e+00 2.21e+02 5.45e-01 1.91e+00 1.59e+10 1 3.22e-01 9.36e+00
14 1.234047e+04 7.90e-01 1.12e+02 4.84e-01 1.87e+00 4.78e+10 1 8.57e-01 1.02e+01
15 1.233986e+04 6.07e-01 1.02e+02 4.22e-01 1.95e+00 1.43e+11 1 6.82e-01 1.09e+01
16 1.233934e+04 5.22e-01 1.03e+02 3.82e-01 1.97e+00 4.30e+11 1 8.30e-01 1.17e+01
17 1.233891e+04 4.25e-01 1.07e+02 3.46e-01 1.93e+00 1.29e+12 1 5.08e-01 1.22e+01
18 1.233855e+04 3.59e-01 1.04e+02 3.15e-01 1.96e+00 3.87e+12 1 1.42e+00 1.37e+01
19 1.233825e+04 3.06e-01 9.27e+01 2.88e-01 1.98e+00 1.16e+13 1 6.68e-01 1.43e+01
20 1.233799e+04 2.61e-01 1.17e+02 2.16e-01 1.97e+00 3.49e+13 1 4.79e-01 1.48e+01
21 1.233777e+04 2.18e-01 1.22e+02 1.15e-01 1.97e+00 1.05e+14 1 3.24e-01 1.51e+01
22 1.233760e+04 1.73e-01 1.10e+02 9.14e-02 1.89e+00 3.14e+14 1 1.06e+00 1.62e+01
23 1.233746e+04 1.37e-01 1.14e+02 1.02e-01 1.98e+00 9.41e+14 1 4.57e-01 1.66e+01
24 1.233735e+04 1.13e-01 1.18e+02 4.15e-01 1.96e+00 2.82e+15 1 1.48e+00 1.81e+01
WARNING: Logging before InitGoogleLogging() is written to STDERR
W1122 19:03:05.843412 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
25 1.233735e+04 0.00e+00 1.18e+02 0.00e+00 0.00e+00 1.41e+15 1 2.44e-01 1.84e+01
26 1.233725e+04 9.50e-02 1.20e+02 3.38e-01 1.99e+00 4.24e+15 1 6.33e-01 1.90e+01
W1122 19:03:06.786262 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
27 1.233725e+04 0.00e+00 1.20e+02 0.00e+00 0.00e+00 2.12e+15 1 3.09e-01 1.93e+01
W1122 19:03:08.919662 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
28 1.233725e+04 0.00e+00 1.20e+02 0.00e+00 0.00e+00 5.30e+14 1 2.13e+00 2.15e+01
29 1.233718e+04 6.92e-02 5.73e+01 1.79e-01 1.70e+00 1.59e+15 1 3.51e-01 2.18e+01
30 1.233714e+04 3.65e-02 5.90e+01 2.64e-01 1.93e+00 4.77e+15 1 6.57e-01 2.25e+01
W1122 19:03:10.162851 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
31 1.233714e+04 0.00e+00 5.90e+01 0.00e+00 0.00e+00 2.38e+15 1 2.35e-01 2.27e+01
32 1.233711e+04 3.32e-02 6.03e+01 3.72e-01 2.00e+00 7.15e+15 1 3.50e-01 2.30e+01
W1122 19:03:12.127734 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
33 1.233711e+04 0.00e+00 6.03e+01 0.00e+00 0.00e+00 3.57e+15 1 1.62e+00 2.47e+01
W1122 19:03:13.732683 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
34 1.233711e+04 0.00e+00 6.03e+01 0.00e+00 0.00e+00 8.94e+14 1 1.60e+00 2.63e+01
35 1.233708e+04 3.14e-02 6.11e+01 1.57e-01 2.00e+00 2.68e+15 1 5.22e-01 2.68e+01
W1122 19:03:15.195761 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
36 1.233708e+04 0.00e+00 6.11e+01 0.00e+00 0.00e+00 1.34e+15 1 9.41e-01 2.77e+01
37 1.233705e+04 2.50e-02 2.63e+01 1.16e+00 1.68e+00 4.02e+15 1 9.47e-01 2.87e+01
W1122 19:03:16.358913 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
38 1.233705e+04 0.00e+00 2.63e+01 0.00e+00 0.00e+00 2.01e+15 1 2.16e-01 2.89e+01
W1122 19:03:17.128914 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
39 1.233705e+04 0.00e+00 2.63e+01 0.00e+00 0.00e+00 5.03e+14 1 7.70e-01 2.97e+01
40 1.233704e+04 1.58e-02 2.05e+01 6.65e-02 1.95e+00 1.51e+15 1 7.94e-01 3.05e+01
41 1.233702e+04 1.51e-02 2.03e+01 2.79e-01 2.00e+00 4.52e+15 1 1.18e+00 3.16e+01
W1122 19:03:20.707713 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
42 1.233702e+04 0.00e+00 2.03e+01 0.00e+00 0.00e+00 2.26e+15 1 1.60e+00 3.32e+01
W1122 19:03:20.973563 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
43 1.233702e+04 0.00e+00 2.03e+01 0.00e+00 0.00e+00 5.65e+14 1 2.66e-01 3.35e+01
44 1.233701e+04 1.48e-02 2.08e+01 1.04e-01 1.99e+00 1.70e+15 1 9.80e-01 3.45e+01
W1122 19:03:22.562964 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
45 1.233701e+04 0.00e+00 2.08e+01 0.00e+00 0.00e+00 8.48e+14 1 6.09e-01 3.51e+01
46 1.233700e+04 1.42e-02 2.08e+01 1.87e-01 1.99e+00 2.54e+15 1 9.93e-01 3.61e+01
W1122 19:03:23.788686 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
47 1.233700e+04 0.00e+00 2.08e+01 0.00e+00 0.00e+00 1.27e+15 1 2.32e-01 3.63e+01
48 1.233698e+04 1.39e-02 2.10e+01 2.29e-01 2.00e+00 3.82e+15 1 6.85e-01 3.70e+01
W1122 19:03:24.716567 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
49 1.233698e+04 0.00e+00 2.10e+01 0.00e+00 0.00e+00 1.91e+15 1 2.43e-01 3.72e+01
W1122 19:03:25.241986 16451 levenberg_marquardt_strategy.cc:115] Linear solver failure. Failed to compute a step: CHOLMOD warning: Matrix not positive definite.
50 1.233698e+04 0.00e+00 2.10e+01 0.00e+00 0.00e+00 4.77e+14 1 5.25e-01 3.78e+01
Solver Summary (v 2.0.0-eigen-(3.4.0)-lapack-suitesparse-(5.7.1)-cxsparse-(3.2.0)-eigensparse-no_openmp)
Original Reduced
Parameter blocks 22122 22122
Parameters 66462 66462
Residual blocks 83718 83718
Residuals 167436 167436
Minimizer TRUST_REGION
Sparse linear algebra library SUITE_SPARSE
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver SPARSE_SCHUR SPARSE_SCHUR
Threads 1 1
Linear solver ordering 11053,11069 11053,11069
Schur structure 2,3,9 2,3,9
Cost:
Initial 1.842900e+07
Final 1.233698e+04
Change 1.841667e+07
Minimizer iterations 51
Successful steps 36
Unsuccessful steps 15
Time (in seconds):
Preprocessor 0.068341
Residual only evaluation 0.573730 (35)
Jacobian & residual evaluation 2.530812 (36)
Linear solver 34.263239 (50)
Minimizer 37.707409
Postprocessor 0.005249
Total 37.781000
Termination: NO_CONVERGENCE (Maximum number of iterations reached. Number of iterations: 50.)
?用MeshLab查看的结果如下:
initial.ply
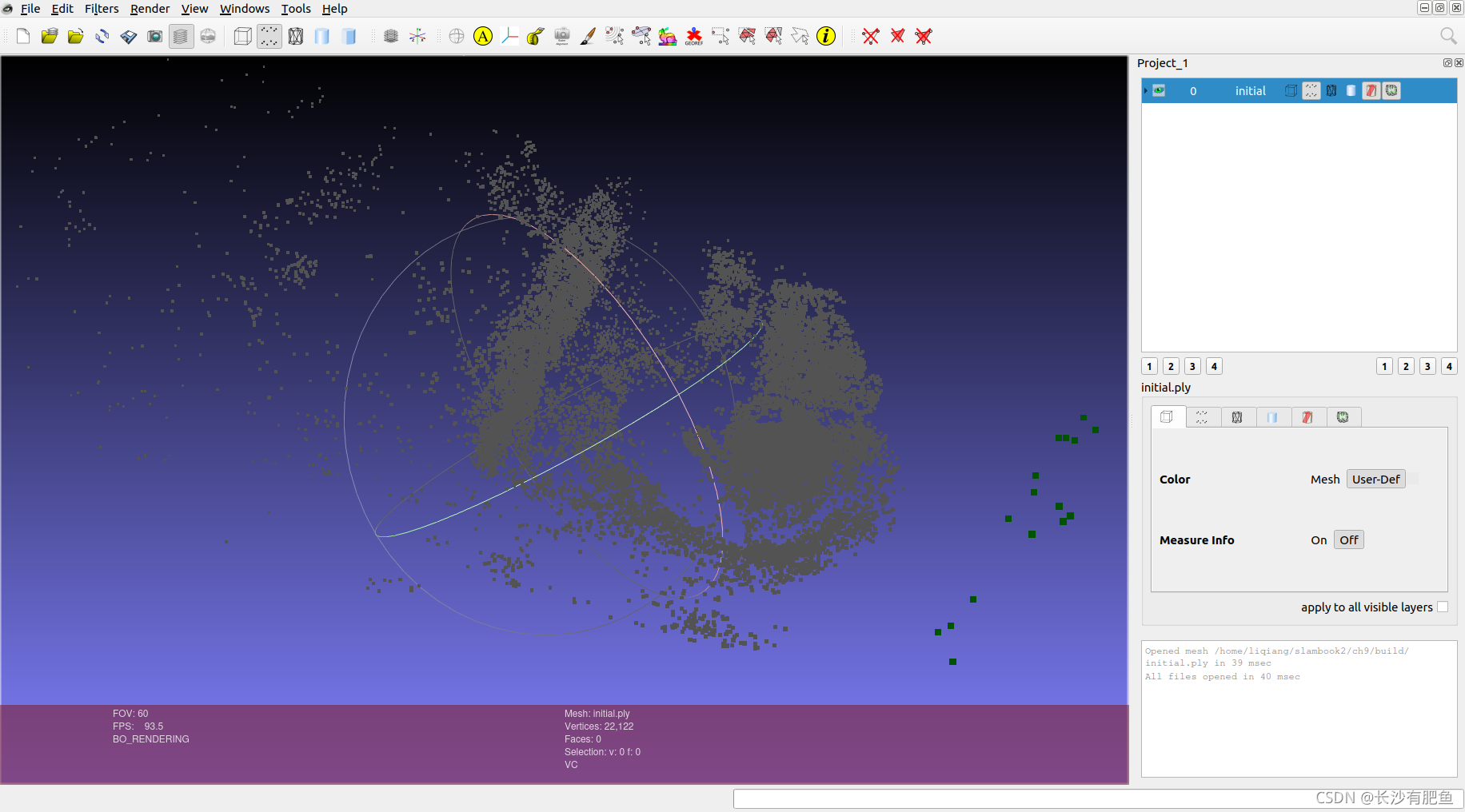
final.ply
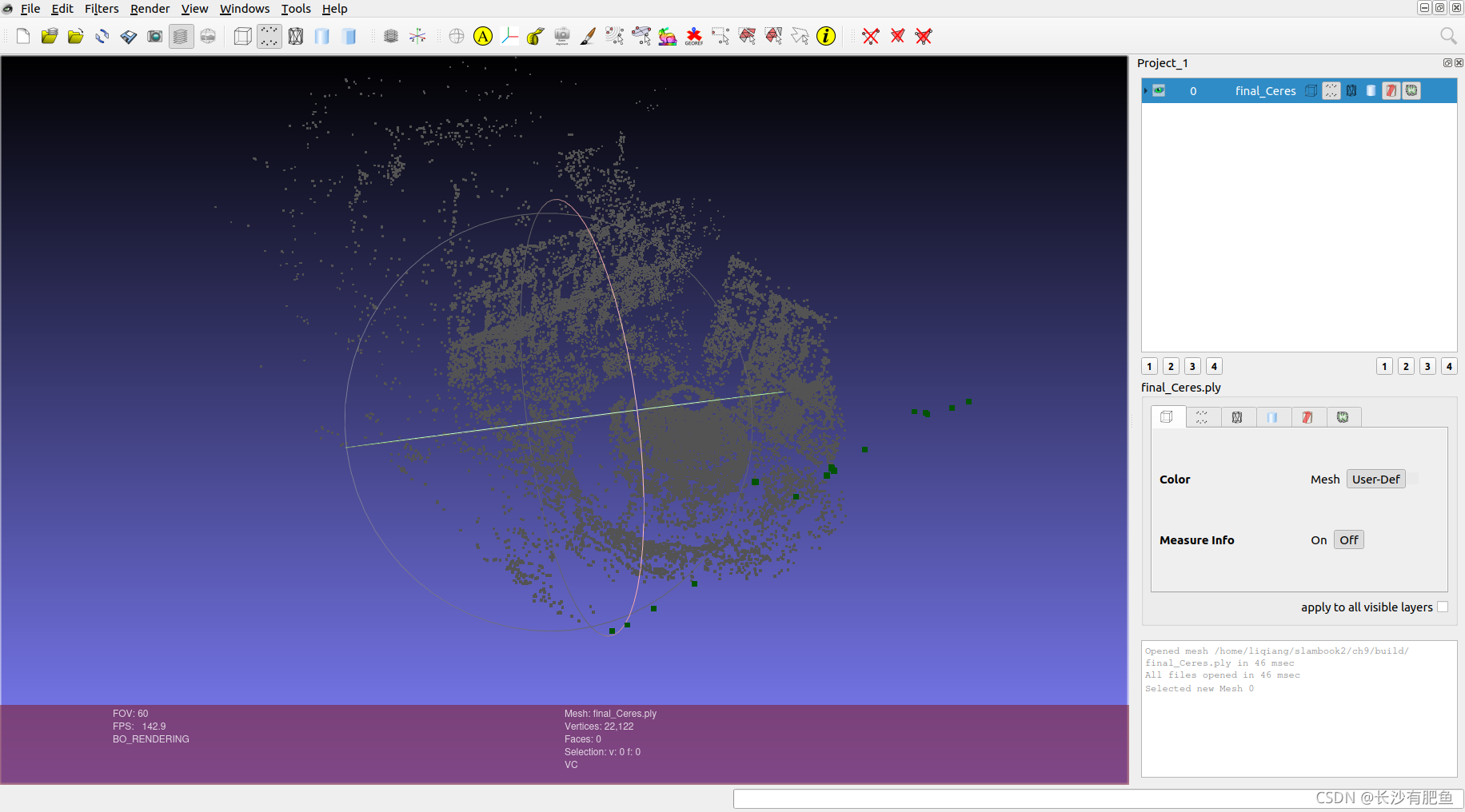
?用CloudCompare查看的结果如下:
initial.ply
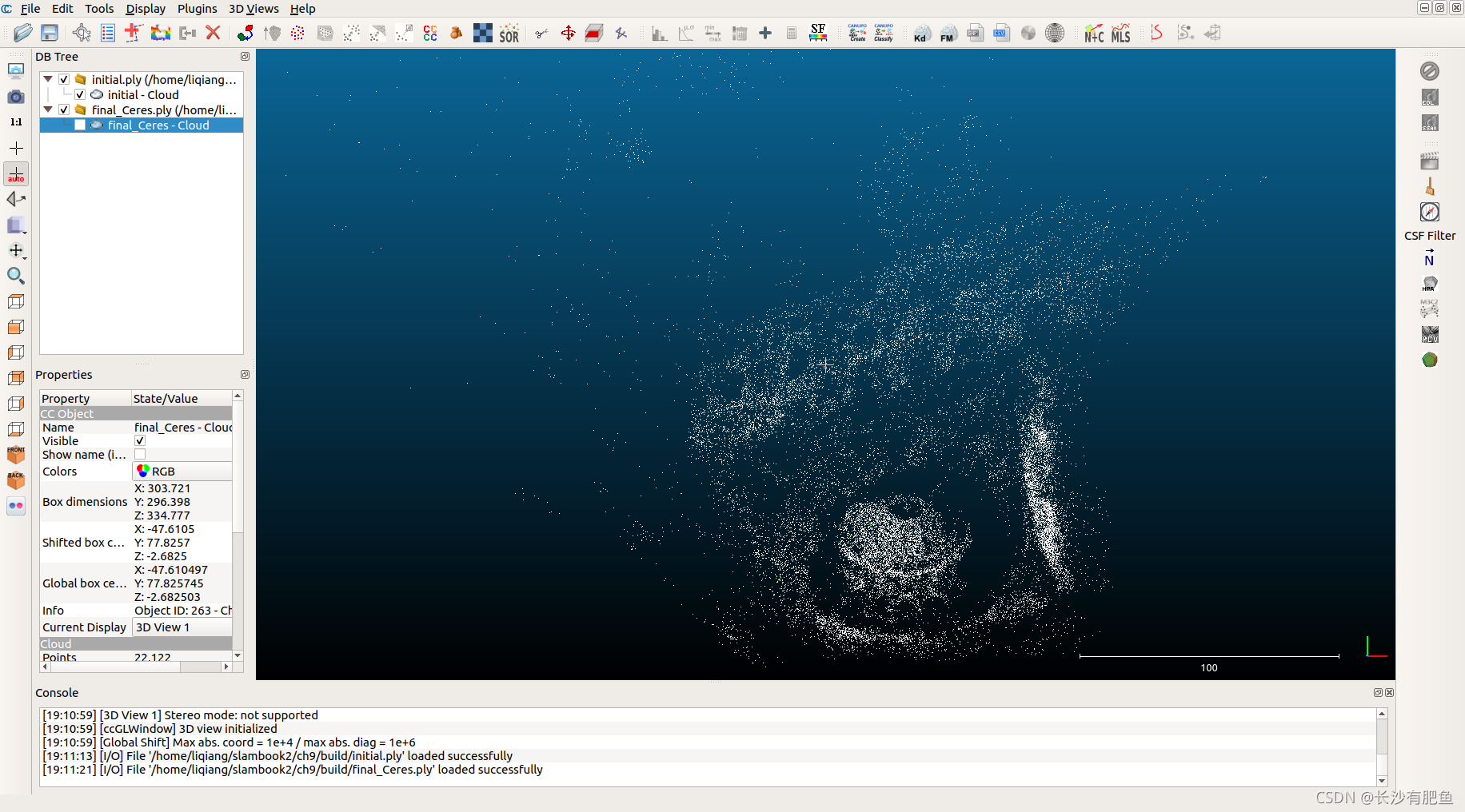
final.ply
??转载于:视觉SLAM十四讲(第二版)第9讲习题解答 - 知乎
4. 证明S矩阵为半正定矩阵。
??转载于:视觉SLAM十四讲(第二版)第9讲习题解答 - 知乎
?
?
?
5. 阅读[36],看看g2o 对核函数是如何处理的。与Ceres 中的Loss function 有何联系?
**************************************************************************
6. *在两个示例中,我们优化了相机位姿、以 f , k1 , k2 为参数的相机内参以及路标点。请考虑使用第五章介绍的完整的相机模型进行优化,即,至少考虑fx,fy,p1,p2,k1,k2 fx?,fy?,p1?,p2?,k1?,k2?这些量。修改现在的Ceres 和g2o 程序以完成实验。
转载于:视觉SLAM十四讲(第二版)第9讲习题解答 - 知乎
代码链接:HW-of-SLAMBOOK2/hw9/p6 at main · Philipcjh/HW-of-SLAMBOOK2 · GitHub
如果你觉得复制麻烦的话,从我的百度网盘里面下载,我写了一些注释。
链接:https://pan.baidu.com/s/1m4G4dPMbGha_zFo5Tg4t2g?
提取码:8888
执行结果:
6_Ceres_completed.cpp
./bundle_adjustment_ceres_completed ../problem-16-22106-pre.txt
Header: 16 22106 83718Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. bal problem file loaded...
bal problem have 16 cameras and 22106 points.
Forming 83718 observations.
Solving ceres BA ...
iter cost cost_change |gradient| |step| tr_ratio tr_radius ls_iter iter_time total_time
0 1.426053e+31 0.00e+00 3.68e+34 0.00e+00 0.00e+00 1.00e+04 0 9.02e-02 2.15e-01
1 1.008312e+37 -1.01e+37 3.68e+34 1.82e+11 -1.41e+06 5.00e+03 1 8.51e-02 3.01e-01
2 4.842222e+35 -4.84e+35 3.68e+34 3.11e+11 -6.79e+04 1.25e+03 1 1.05e-01 4.06e-01
3 6.188762e+33 -6.17e+33 3.68e+34 7.42e+11 -8.66e+02 1.56e+02 1 1.03e-01 5.09e-01
4 2.614653e+43 -2.61e+43 3.68e+34 1.37e+12 -3.67e+12 9.77e+00 1 1.08e-01 6.18e-01
5 2.929472e+47 -2.93e+47 3.68e+34 1.15e+12 -4.11e+16 3.05e-01 1 1.07e-01 7.25e-01
6 2.178687e+41 -2.18e+41 3.68e+34 2.96e+11 -3.25e+10 4.77e-03 1 1.07e-01 8.31e-01
7 4.184920e+35 -4.18e+35 3.68e+34 6.13e+09 -6.45e+05 3.73e-05 1 1.05e-01 9.37e-01
8 1.425515e+31 5.39e+27 3.68e+34 5.01e+07 9.90e-01 1.12e-04 1 2.11e-01 1.15e+00
9 1.423901e+31 1.61e+28 3.68e+34 1.45e+09 1.00e+00 3.35e-04 1 1.85e-01 1.33e+00
10 1.419087e+31 4.81e+28 3.66e+34 1.21e+10 1.00e+00 1.01e-03 1 1.80e-01 1.51e+00
11 1.404909e+31 1.42e+29 3.62e+34 7.59e+10 1.00e+00 3.02e-03 1 1.85e-01 1.70e+00
12 1.363402e+31 4.15e+29 3.50e+34 1.02e+12 1.00e+00 9.05e-03 1 1.86e-01 1.88e+00
13 1.253174e+31 1.10e+30 3.18e+34 8.45e+12 9.99e-01 2.72e-02 1 1.86e-01 2.07e+00
14 1.044141e+31 2.09e+30 1.93e+34 3.20e+13 8.72e-01 4.61e-02 1 1.86e-01 2.25e+00
15 3.207461e+31 -2.16e+31 1.93e+34 1.75e+14 -9.41e+00 2.30e-02 1 7.77e-02 2.33e+00
16 9.036078e+30 1.41e+30 1.65e+34 1.05e+14 1.01e+00 6.91e-02 1 2.09e-01 2.54e+00
17 8.286968e+30 7.49e+29 2.66e+35 2.54e+14 2.99e-01 6.49e-02 1 1.79e-01 2.72e+00
18 7.190000e+30 1.10e+30 1.42e+35 2.52e+14 4.68e-01 6.49e-02 1 1.86e-01 2.91e+00
19 5.029735e+31 -4.31e+31 1.42e+35 2.46e+14 -2.20e+01 3.24e-02 1 7.81e-02 2.98e+00
20 5.913780e+30 1.28e+30 1.12e+35 1.52e+14 1.01e+00 9.73e-02 1 2.09e-01 3.19e+00
21 3.895439e+30 2.02e+30 6.83e+34 2.46e+14 1.04e+00 2.92e-01 1 1.86e-01 3.38e+00
22 6.451373e+31 -6.06e+31 6.83e+34 2.03e+14 -3.48e+01 1.46e-01 1 8.43e-02 3.46e+00
23 8.985577e+30 -5.09e+30 6.83e+34 1.41e+14 -3.43e+00 3.65e-02 1 1.07e-01 3.57e+00
24 3.157985e+30 7.37e+29 5.28e+34 6.72e+13 1.01e+00 1.09e-01 1 2.07e-01 3.78e+00
25 4.685928e+30 -1.53e+30 5.28e+34 1.91e+14 -1.40e+00 5.47e-02 1 8.29e-02 3.86e+00
26 2.368461e+30 7.90e+29 3.73e+34 1.30e+14 1.02e+00 1.64e-01 1 2.12e-01 4.07e+00
27 1.481967e+30 8.86e+29 1.40e+35 2.11e+14 9.46e-01 4.93e-01 1 1.83e-01 4.26e+00
28 4.679656e+30 -3.20e+30 1.40e+35 1.41e+14 -4.53e+00 2.46e-01 1 8.20e-02 4.34e+00
29 2.100742e+31 -1.95e+31 1.40e+35 1.18e+14 -3.02e+01 6.16e-02 1 1.05e-01 4.44e+00
30 1.056929e+30 4.25e+29 4.74e+34 7.08e+13 1.04e+00 1.85e-01 1 2.11e-01 4.66e+00
31 5.467407e+32 -5.46e+32 4.74e+34 1.03e+14 -1.27e+03 9.24e-02 1 8.24e-02 4.74e+00
32 7.092017e+29 3.48e+29 1.27e+34 8.10e+13 1.02e+00 2.77e-01 1 2.05e-01 4.94e+00
33 3.803746e+29 3.29e+29 4.81e+33 9.20e+13 1.08e+00 8.32e-01 1 1.84e-01 5.13e+00
34 1.645500e+29 2.16e+29 1.71e+33 1.53e+14 1.17e+00 2.49e+00 1 1.80e-01 5.31e+00
35 2.481753e+30 -2.32e+30 1.71e+33 9.50e+13 -2.83e+01 1.25e+00 1 8.29e-02 5.39e+00
36 3.379389e+29 -1.73e+29 1.71e+33 7.89e+13 -2.14e+00 3.12e-01 1 1.09e-01 5.50e+00
37 8.709032e+28 7.75e+28 8.26e+32 4.29e+13 1.09e+00 9.35e-01 1 2.09e-01 5.71e+00
38 3.758940e+28 4.95e+28 3.31e+32 7.02e+13 1.17e+00 2.81e+00 1 1.84e-01 5.89e+00
39 1.447295e+28 2.31e+28 1.21e+32 5.62e+13 1.24e+00 8.42e+00 1 1.88e-01 6.08e+00
40 5.215108e+27 9.26e+27 5.81e+31 2.03e+13 1.28e+00 2.53e+01 1 1.88e-01 6.27e+00
41 2.598177e+27 2.62e+27 4.01e+32 1.27e+13 1.00e+00 7.58e+01 1 1.86e-01 6.45e+00
42 5.998289e+28 -5.74e+28 4.01e+32 2.08e+13 -4.42e+01 3.79e+01 1 8.29e-02 6.54e+00
43 8.879112e+26 1.71e+27 1.37e+32 1.31e+13 1.32e+00 1.14e+02 1 2.06e-01 6.74e+00
44 6.137729e+26 2.74e+26 1.32e+32 1.14e+13 6.18e-01 1.15e+02 1 1.85e-01 6.93e+00
45 2.636900e+27 -2.02e+27 1.32e+32 7.16e+12 -6.59e+00 5.76e+01 1 8.48e-02 7.01e+00
46 6.345956e+27 -5.73e+27 1.32e+32 5.80e+12 -1.87e+01 1.44e+01 1 1.08e-01 7.12e+00
47 4.407903e+31 -4.41e+31 1.32e+32 2.33e+12 -1.44e+05 1.80e+00 1 1.10e-01 7.23e+00
48 7.113510e+35 -7.11e+35 1.32e+32 1.68e+11 -2.34e+09 1.12e-01 1 1.08e-01 7.34e+00
49 3.967797e+26 2.17e+26 7.54e+31 5.16e+10 1.04e+00 3.37e-01 1 2.10e-01 7.55e+00
50 1.961998e+26 2.01e+26 3.30e+31 1.37e+11 1.13e+00 1.01e+00 1 1.81e-01 7.73e+00
Solver Summary (v 2.0.0-eigen-(3.4.0)-lapack-suitesparse-(5.7.1)-cxsparse-(3.2.0)-eigensparse-no_openmp)
Original Reduced
Parameter blocks 22122 22122
Parameters 66510 66510
Residual blocks 83718 83718
Residuals 167436 167436
Minimizer TRUST_REGION
Sparse linear algebra library SUITE_SPARSE
Trust region strategy LEVENBERG_MARQUARDT
Given Used
Linear solver SPARSE_SCHUR SPARSE_SCHUR
Threads 1 1
Linear solver ordering AUTOMATIC 22106,16
Schur structure 2,3,12 2,3,d
Cost:
Initial 1.426053e+31
Final 1.961998e+26
Change 1.426034e+31
Minimizer iterations 51
Successful steps 29
Unsuccessful steps 22
Time (in seconds):
Preprocessor 0.125221
Residual only evaluation 0.829317 (50)
Jacobian & residual evaluation 2.835020 (29)
Linear solver 3.583899 (50)
Minimizer 7.606891
Postprocessor 0.003257
Total 7.735369
Termination: NO_CONVERGENCE (Maximum number of iterations reached. Number of iterations: 50.)6_g2o_completed.cpp
./bundle_adjustment_g2o_completed ../problem-16-22106-pre.txt Header: 16 22106 83718Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. Invalid UW data file. iteration= 0 chi2= 11448902579012400459871397347328.000000 time= 0.259172 cumTime= 0.259172 edges= 83718 schur= 1 lambda= 530700671390243807692080956833792.000000 levenbergIter= 1
iteration= 1 chi2= 4595260219343684448692142604288.000000 time= 0.230507 cumTime= 0.489678 edges= 83718 schur= 1 lambda= 176900223796747911878162306301952.000000 levenbergIter= 1
iteration= 2 chi2= 1844418264889403638802200657920.000000 time= 0.231039 cumTime= 0.720717 edges= 83718 schur= 1 lambda= 58966741265582631287921265606656.000000 levenbergIter= 1
iteration= 3 chi2= 740659536427463787514855161856.000000 time= 0.23078 cumTime= 0.951497 edges= 83718 schur= 1 lambda= 19655580421860876345373817307136.000000 levenbergIter= 1
iteration= 4 chi2= 297997717305666076069010079744.000000 time= 0.230924 cumTime= 1.18242 edges= 83718 schur= 1 lambda= 6551860140620291739824636821504.000000 levenbergIter= 1
iteration= 5 chi2= 120132864063713142033520525312.000000 time= 0.231252 cumTime= 1.41367 edges= 83718 schur= 1 lambda= 2183953380206763819449886703616.000000 levenbergIter= 1
iteration= 6 chi2= 48492549339466582870215098368.000000 time= 0.230615 cumTime= 1.64429 edges= 83718 schur= 1 lambda= 727984460068921226237466116096.000000 levenbergIter= 1
iteration= 7 chi2= 19607328009167539406754545664.000000 time= 0.23144 cumTime= 1.87573 edges= 83718 schur= 1 lambda= 242661486689640397017698009088.000000 levenbergIter= 1
iteration= 8 chi2= 7946374249468844297911533568.000000 time= 0.230603 cumTime= 2.10633 edges= 83718 schur= 1 lambda= 80887162229880132339232669696.000000 levenbergIter= 1
iteration= 9 chi2= 3229669490728618606303641600.000000 time= 0.230941 cumTime= 2.33727 edges= 83718 schur= 1 lambda= 26962387409960042647062052864.000000 levenbergIter= 1
iteration= 10 chi2= 1317245444053740616599732224.000000 time= 0.23097 cumTime= 2.56824 edges= 83718 schur= 1 lambda= 8987462469986680515850141696.000000 levenbergIter= 1
iteration= 11 chi2= 539852484883824402979880960.000000 time= 0.231086 cumTime= 2.79933 edges= 83718 schur= 1 lambda= 2995820823328893138779504640.000000 levenbergIter= 1
iteration= 12 chi2= 222523785803762087938228224.000000 time= 0.230812 cumTime= 3.03014 edges= 83718 schur= 1 lambda= 998606941109631046259834880.000000 levenbergIter= 1
iteration= 13 chi2= 92228822367983213205258240.000000 time= 0.230748 cumTime= 3.26089 edges= 83718 schur= 1 lambda= 332868980369877015419944960.000000 levenbergIter= 1
iteration= 14 chi2= 38407193365467773615996928.000000 time= 0.230722 cumTime= 3.49161 edges= 83718 schur= 1 lambda= 110956326789958999413358592.000000 levenbergIter= 1
iteration= 15 chi2= 16056314699064937797386240.000000 time= 0.230833 cumTime= 3.72244 edges= 83718 schur= 1 lambda= 36985442263319663607808000.000000 levenbergIter= 1
iteration= 16 chi2= 6734886581315290875822080.000000 time= 0.230534 cumTime= 3.95298 edges= 83718 schur= 1 lambda= 12328480754439886437613568.000000 levenbergIter= 1
iteration= 17 chi2= 2829306185676062361387008.000000 time= 0.230895 cumTime= 4.18387 edges= 83718 schur= 1 lambda= 4109493584813295300247552.000000 levenbergIter= 1
iteration= 18 chi2= 1180828120018257134485504.000000 time= 0.230913 cumTime= 4.41478 edges= 83718 schur= 1 lambda= 1369831194937765010604032.000000 levenbergIter= 1
iteration= 19 chi2= 476259064945792176357376.000000 time= 0.230834 cumTime= 4.64562 edges= 83718 schur= 1 lambda= 456610398312588292128768.000000 levenbergIter= 1
iteration= 20 chi2= 172223130510230229614592.000000 time= 0.230728 cumTime= 4.87635 edges= 83718 schur= 1 lambda= 152203466104196097376256.000000 levenbergIter= 1
iteration= 21 chi2= 53259651355799862640640.000000 time= 0.230701 cumTime= 5.10705 edges= 83718 schur= 1 lambda= 50734488701398696329216.000000 levenbergIter= 1
iteration= 22 chi2= 17376547137931345657856.000000 time= 0.230627 cumTime= 5.33767 edges= 83718 schur= 1 lambda= 16911496233799565443072.000000 levenbergIter= 1
iteration= 23 chi2= 5578663258492342632448.000000 time= 0.230643 cumTime= 5.56832 edges= 83718 schur= 1 lambda= 5637165411266521464832.000000 levenbergIter= 1
iteration= 24 chi2= 2311970972739212148736.000000 time= 0.23078 cumTime= 5.7991 edges= 83718 schur= 1 lambda= 1879055137088840400896.000000 levenbergIter= 1
iteration= 25 chi2= 959849145519869001728.000000 time= 0.231137 cumTime= 6.03023 edges= 83718 schur= 1 lambda= 626351712362946756608.000000 levenbergIter= 1
iteration= 26 chi2= 382583584621919207424.000000 time= 0.230728 cumTime= 6.26096 edges= 83718 schur= 1 lambda= 208783904120982241280.000000 levenbergIter= 1
iteration= 27 chi2= 143775983664472834048.000000 time= 0.230823 cumTime= 6.49178 edges= 83718 schur= 1 lambda= 69594634706994077696.000000 levenbergIter= 1
iteration= 28 chi2= 49769152496296599552.000000 time= 0.231674 cumTime= 6.72346 edges= 83718 schur= 1 lambda= 23198211568998023168.000000 levenbergIter= 1
iteration= 29 chi2= 19489607644068515840.000000 time= 0.231787 cumTime= 6.95524 edges= 83718 schur= 1 lambda= 7732737189666007040.000000 levenbergIter= 1
iteration= 30 chi2= 10393343318164428800.000000 time= 0.231142 cumTime= 7.18639 edges= 83718 schur= 1 lambda= 2577579063222002176.000000 levenbergIter= 1
iteration= 31 chi2= 5605414270446759936.000000 time= 0.231288 cumTime= 7.41768 edges= 83718 schur= 1 lambda= 859193021074000640.000000 levenbergIter= 1
iteration= 32 chi2= 2996642648132236288.000000 time= 0.231316 cumTime= 7.64899 edges= 83718 schur= 1 lambda= 286397673691333536.000000 levenbergIter= 1
iteration= 33 chi2= 1573007263301203712.000000 time= 0.230242 cumTime= 7.87923 edges= 83718 schur= 1 lambda= 95465891230444512.000000 levenbergIter= 1
iteration= 34 chi2= 804389888780158208.000000 time= 0.230831 cumTime= 8.11007 edges= 83718 schur= 1 lambda= 31821963743481504.000000 levenbergIter= 1
iteration= 35 chi2= 397544280164181824.000000 time= 0.230988 cumTime= 8.34105 edges= 83718 schur= 1 lambda= 10607321247827168.000000 levenbergIter= 1
iteration= 36 chi2= 187995528807614912.000000 time= 0.230492 cumTime= 8.57155 edges= 83718 schur= 1 lambda= 3535773749275722.500000 levenbergIter= 1
iteration= 37 chi2= 83317161800343920.000000 time= 0.230595 cumTime= 8.80214 edges= 83718 schur= 1 lambda= 1178591249758574.000000 levenbergIter= 1
iteration= 38 chi2= 31937020605604204.000000 time= 0.230731 cumTime= 9.03287 edges= 83718 schur= 1 lambda= 392863749919524.625000 levenbergIter= 1
iteration= 39 chi2= 7428030063663569.000000 time= 0.230605 cumTime= 9.26348 edges= 83718 schur= 1 lambda= 130954583306508.203125 levenbergIter= 1