梯度下降
1.概念
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。梯度下降(Gradient Descent)是在求解机器学习算法的模型参数最常采用的方法之一(另外一种是最小二乘法)。在求解损失函数的最小值时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。
2.梯度
梯度下降法的计算过程就是沿梯度下降的方向求解极小值的过程,我们首先要知道梯度的数学意义以及表达式,在单变量函数中,梯度就是函数的微分
例如
d
(
x
2
)
d
(
x
)
=
2
x
\frac{d(x^2)}{d(x)}=2x
d(x)d(x2)?=2x,
d
(
?
2
y
3
)
d
(
y
)
=
?
6
y
2
\frac{d(-2y^3)}{d(y)}=-6y^2
d(y)d(?2y3)?=?6y2。对于多变量的微分,当函数有多个变量时,分别对每一个变量求微分,例如
?
?
x
\frac{\partial}{\partial x}
?x??
(
x
2
y
2
)
(x^2y^2)
(x2y2)=
2
x
y
2
2xy^2
2xy2,
?
?
y
\frac{\partial}{\partial y}
?y??
(
?
y
4
+
z
2
)
(-y^4 + z^2)
(?y4+z2)=
?
4
y
3
-4y^3
?4y3。对于一元函数来讲,梯度就是函数的导数。而对于多元函数而言,梯度是一个向量,也就是说,把求得的偏导数以向量的形式写出来,就是梯度。
3.梯度下降
梯度下降就是通过一步一步的迭代,让所有的编导函数都下降到最低,用数学公式来描述就是
x
k
+
1
x_{k+1}
xk+1?=
x
k
x_k
xk? -
α
\alpha
α
?
\cdot
?g 。
x
k
x_k
xk?为k时刻的点坐标,
x
k
+
1
x_{k+1}
xk+1?为下一刻要移动的点的坐标,例如
x
0
x_0
x0?就代表初始化的点的坐标,
x
1
x_1
x1?就代表第一部移动到的位置。
g代表梯度,前边有个负号,就代表朝着梯度相反的方向移动,也即梯度下降。
α
\alpha
α代表学习率(也叫做步长)。用它乘以梯度值来控制每次移动的距离,
α
\alpha
α的值需要自己设置,如果过大,容易一步跨太大,直接跳过了最小值,设置太小则会导致迭代次数过多。
4.简单示例分析
下面以简单的一元函数来进行实例分析:
y
=
(
x
?
2.5
)
2
+
3
y=(x-2.5)^2+3
y=(x?2.5)2+3
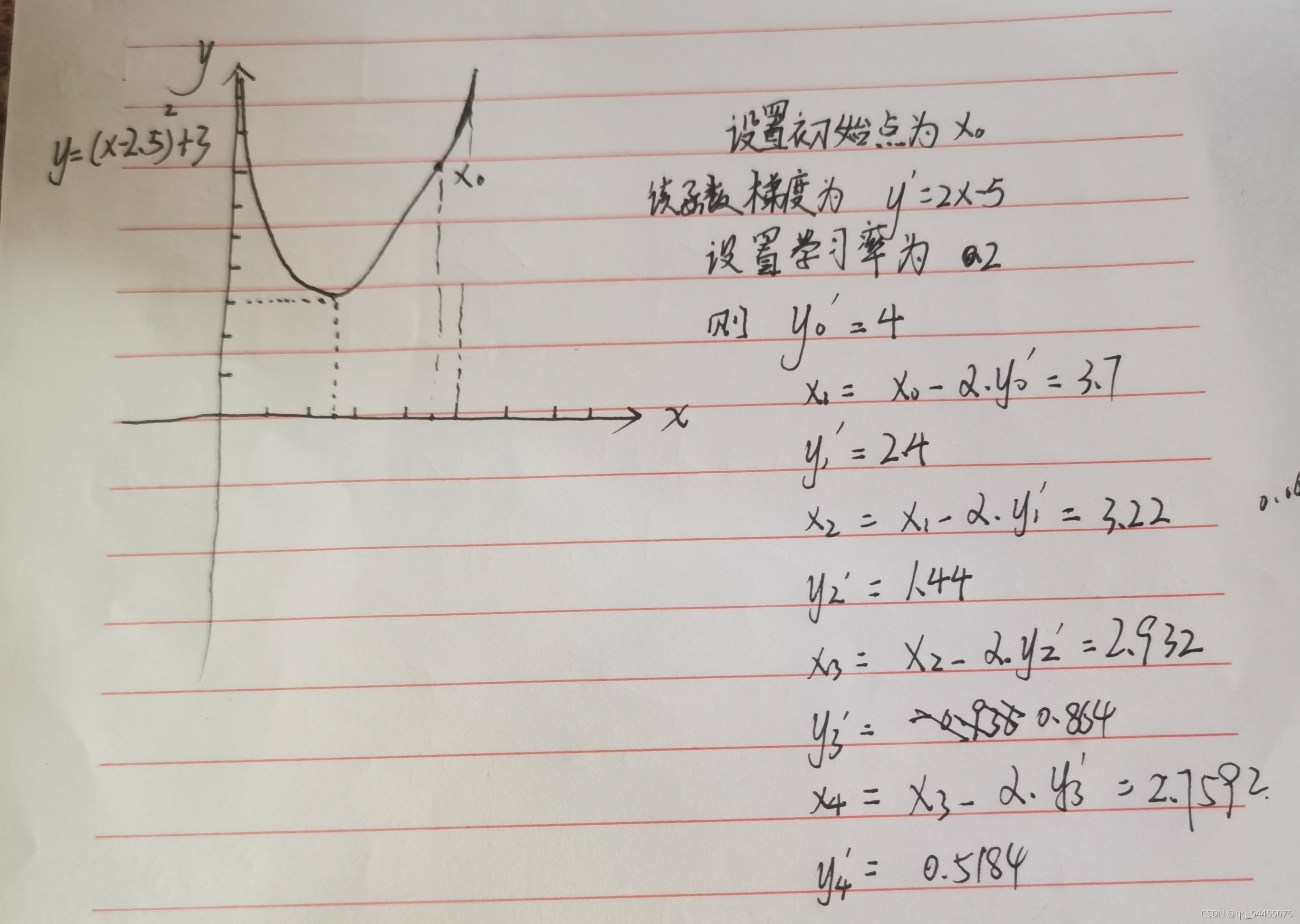
多元函数的思路也一样,先初始化一个点,计算它的梯度,然后往梯度相反的方向,每次移动一点点,直到达到停止条件。这个停止条件,可以是足够大的迭代步数,也可以是一个比较小的阈值,当两次迭代之间的差值小于该阈值时,认为梯度已经下降到最低点附近了。
5.代码实现
import numpy as np
import matplotlib.pyplot as plt
x = eval(input("输入初始的x的位置:"))
ap = eval(input("输入学习率:"))
i = 0
x11 = list()
y11 = list()
sl = list()
for i in range(10000):
y = (x - 2.5) ** 2 + 3
y1 = 2 * x - 5
ak = [x, y]
x11.append(x)
y11.append(y)
x = x - ap * y1
sl.append(ak)
i += 1
if abs(x - 2.5) < 1e-5:
print("运行次数为:", i)
print("坐标分别是:")
for e in sl:
print(e, end="")
break
elif i > 500:
print("迭代次数过多,学习率过小")
break
plt.plot(x11, y11)
plt.show()
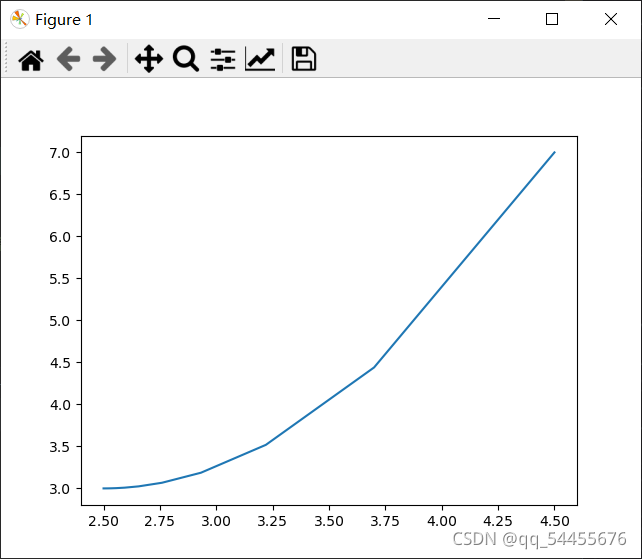
6.总结
本文只是讲解了梯度下降的最简单的一种形式,有很多概念以及函数未涉及到,在之后的文章里会慢慢补充。