引言

在评估聚类效果的时候，常常使用NMI和ARI，即归一化互信息和调整兰德指数，但这两个指标是以结果为导向的，无论采用了何种聚类方式。但NMI和ARI只能告诉你聚类结果好不好，却无法知道你的聚类方法是否在有效工作。

在目前最流行的子空间聚类方法中，我们是通过构造coeff矩阵C来得到affinty A，之后通过谱聚类（spectral clustering）得到partition Q。子空间聚类已被证明和self-attention机制是密切相关的，因此是高效的，但也具有和self-attention一样的平方复杂度缺陷。

要了解子空间聚类是否真的在有效工作，就要评估系数矩阵C，这便是SRE和CONN这两个指标。，如接下来所介绍的那样。

Evaluation Metrics

聚类准确度（Clustering accuracy, ACC）

相比于有标签的准确度，聚类准确度的计算更加麻烦些，它是依据ground truth和分割矩阵Q来计算的。在实践中，ACC的好坏与否与ARI指标高度相关。如果ACC不理想，想办法提高ARI先！

acc指标表示了预测结果和ground truth之间的差距：

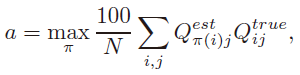
在这里插入图片描述
其中，有个100倍的系数是因为输出是百分比值，est即为estimation的缩写，true就是ground truth。当第j个点属于第i个cluster时，这两个Q在第 $(i, j)$ 个元素为1，否则为0，也就是说Q的每行都是one-hot的。需要注意，其中 $\pi$ 表示n个cluster的组合，因为聚类得到的是伪标签，必须用如匈牙利算法把伪标签和ground truth最大匹配起来。

子空间保持误差（SRE）

SRE有两种写法：Subspace Recovery Error和 Subspace-preserving Representation Error，但其实都表示一个意思，就是衡量了C的子空间保持性质，SRE越低说明了误差越小，连通的分量 $c_{ij}$ 大都来自相同的子空间。
具体地，对于每个 $c_j$ ，我们计算它的来自其他子空间的 $\ell_1$ 范数的分数，对所有 $j$ 做求和平均：
在这里插入图片描述
其中 $w_{ij}\in \{0,1\}$ 为true affinity。

给出SRE的pytorch实现：

def subspace_preserving_error(A, labels, n_clusters): # that is, SRE
    one_hot_labels = torch.zeros([A.shape[0], n_clusters])
    for i in range(A.shape[0]):
        one_hot_labels[i][labels[i]] = 1.0
    mask = one_hot_labels.matmul(one_hot_labels.T)
    l1_norm = torch.norm(A, p=1, dim=1)
    masked_l1_norm = torch.norm(mask * A, p=1, dim=1)
    e = torch.mean((1. - masked_l1_norm / l1_norm)) * 100.
    return e

连通性（Connectivity, CONN）

connectivity衡量了C的连通性。我们希望低的SRE，但是过低的SRE往往会让C过于稀疏而在谱聚类时产生过分割最终影响聚类结果，因此我们希望连通性要高点好：CONN度量了同一个cluster中C的稠密程度，即我们希望同一类中的尽量不要出现 $c_{ij}=0$ 。

所以，显然SRE和CONN是一对矛盾的指标，CONN提高往往导致SRE变差，SRE降低往往导致CONN下降。**子空间聚类方法好不好还要考虑到它能不能有效权衡SRE和CONN。**实验也证明，只有CONN和SRE取得一个合理的balance的时候聚类精度才上得去。

不过，CONN的计算比较反直觉，这里介绍代数连通性（algebratic connectivity），它的定义是：归一化后的图拉普拉斯矩阵的第二小的特征值。对于一个无向权重图，权重为 $W\in\mathbb R^{N\times N}$ 和度矩阵 $D=diag(W\cdot 1)$ ，那么它的归一化图拉普拉斯为：
在这里插入图片描述
取 $L$ 的第二个eigen value $\lambda_2 \in [0,\frac{n-1}{n}]$ 。为了评估具有n个cluster的affinity gpraph的连通性，我们计算每个n个子图的第二最小特征值，那么就得到了n个对应于第 $i$ 个cluster的特征值 $\{\lambda_2^{(i)}\}_{i=1}^n$ 。对于CONN有两种计算方法：取最小值或求平均值：
在这里插入图片描述
取最小值的话，实际中conn容易很小，比如 $10^{-16}$ 量级，这个时候考虑取平均值：

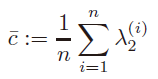
在这里插入图片描述

小技巧：合成数据集上用最小值，真实数据集上用平均值

给出归一化图拉普拉斯的实现：

def normalized_laplacian(A): 
    D = torch.sum(A, dim=1)
    D_sqrt = torch.diag(1.0 / torch.sqrt(D))
    L = torch.eye(A.shape[0]) - D_sqrt.matmul(A).matmul(D_sqrt)
    return L

CONN的pytorch实现：

def connectivity(A, labels, n_clusters): # A is dense tensor
    c = []
    for i in range(n_clusters):
        A_i = A[labels == i][:, labels == i]
        L_i = normalized_laplacian(A_i)
        eig_vals, _ = torch.symeig(L_i)
        c.append(eig_vals[1])
    return np.min(c)

def sparse_connectivity(A, labels, n_clusters): # A is sparse tensor
    c = []
    for i in range(n_clusters):
        A_i = A[labels == i][:, labels == i]
        L_i = csgraph.laplacian(A_i) # L = D - W
        eig_vals, _ = sparse.linalg.eigsh(L_i, k=2, which='SA')
        eig_vals = sorted(eig_vals)
        c.append(eig_vals[1])
    return np.mean(c)