1 调查背景
1.1 廉政建设的持续推进
当今,倡导政府工作人员履职公正廉洁,不因私欲滥用权制。廉政作为植根于民族文化中的传统美德,更是民众应当推崇的,抨击社会腐败之风对我们来说义不容辞。中国政府决心继续推进党风廉政建设,中共中央也提出反腐倡廉教育要面向全党全社会,需要大力加强廉政文化建设。这些均表明:推进廉政建设是当今社会主流。
1.2 调查廉政的意义
廉政是社会生活的重要组成部分,对廉政情况的调研及分析成为了社会生活指数调查的主导因素之一。透过调查结果,我们可以在一定程度上感知到民众对廉政现状的看法,包括对廉政相关事件、措施的了解程度,对廉政治理情况的态度等。
2 调查实施
2.1 调查内容
采用调查问卷的形式,有目标性地引导身边的亲友、长辈填写问卷(受疫情影响,本次调查以纯线上的形式展开)并将收集到的答卷结果与组内其他成员进行汇总,随后进一步展开分析及报告撰写等工作。
2.2 问卷设计
问卷包含受访者个人信息(性别、年龄、学历、职业、月收入、居住地),对廉政的关注程度及渠道,对廉政相关事件的认知及了解程度,对廉政治理情况的态度等。
3 答卷收集情况
3.1 收集总数
共收集答卷1554份,均完成问卷全部问题。
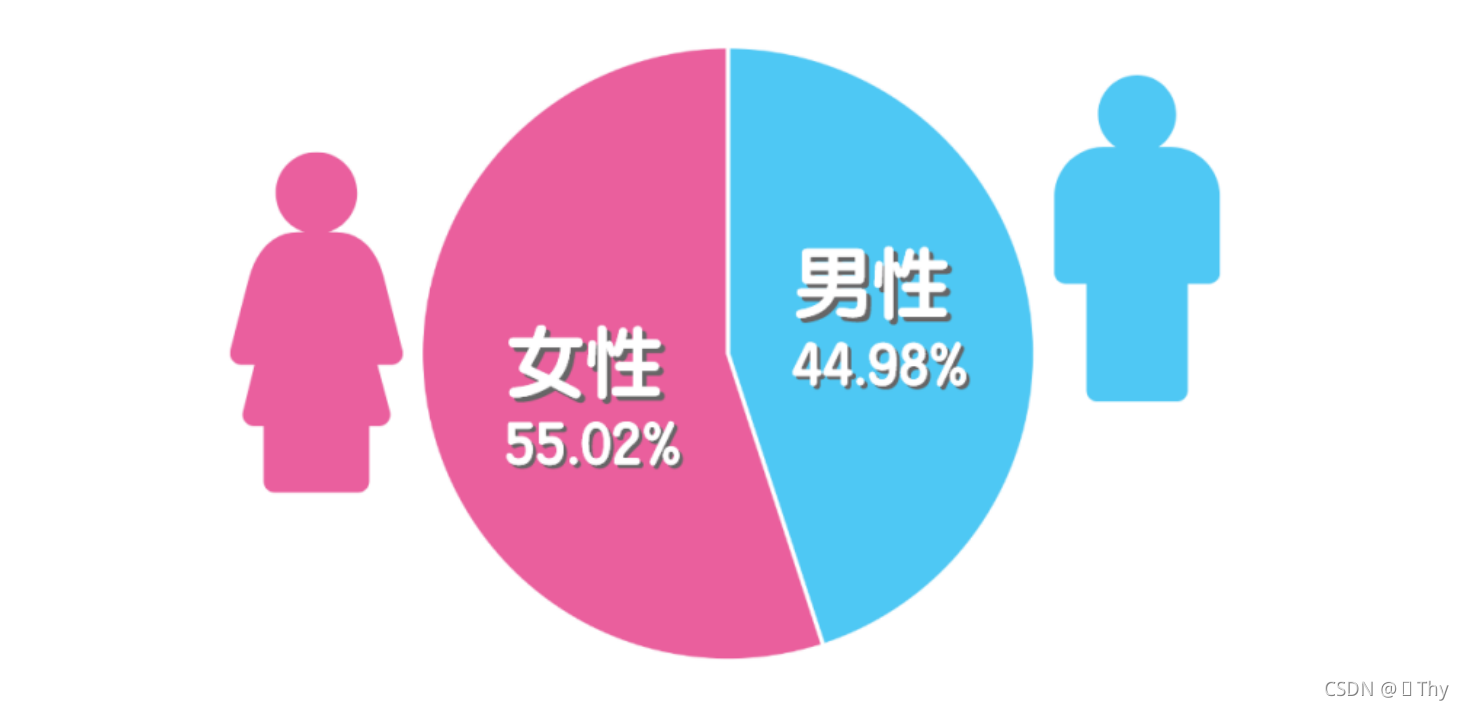
3.2 性别分布
全部1554位受访者中,男性有699人,女性855人。
3.3 居住地分布
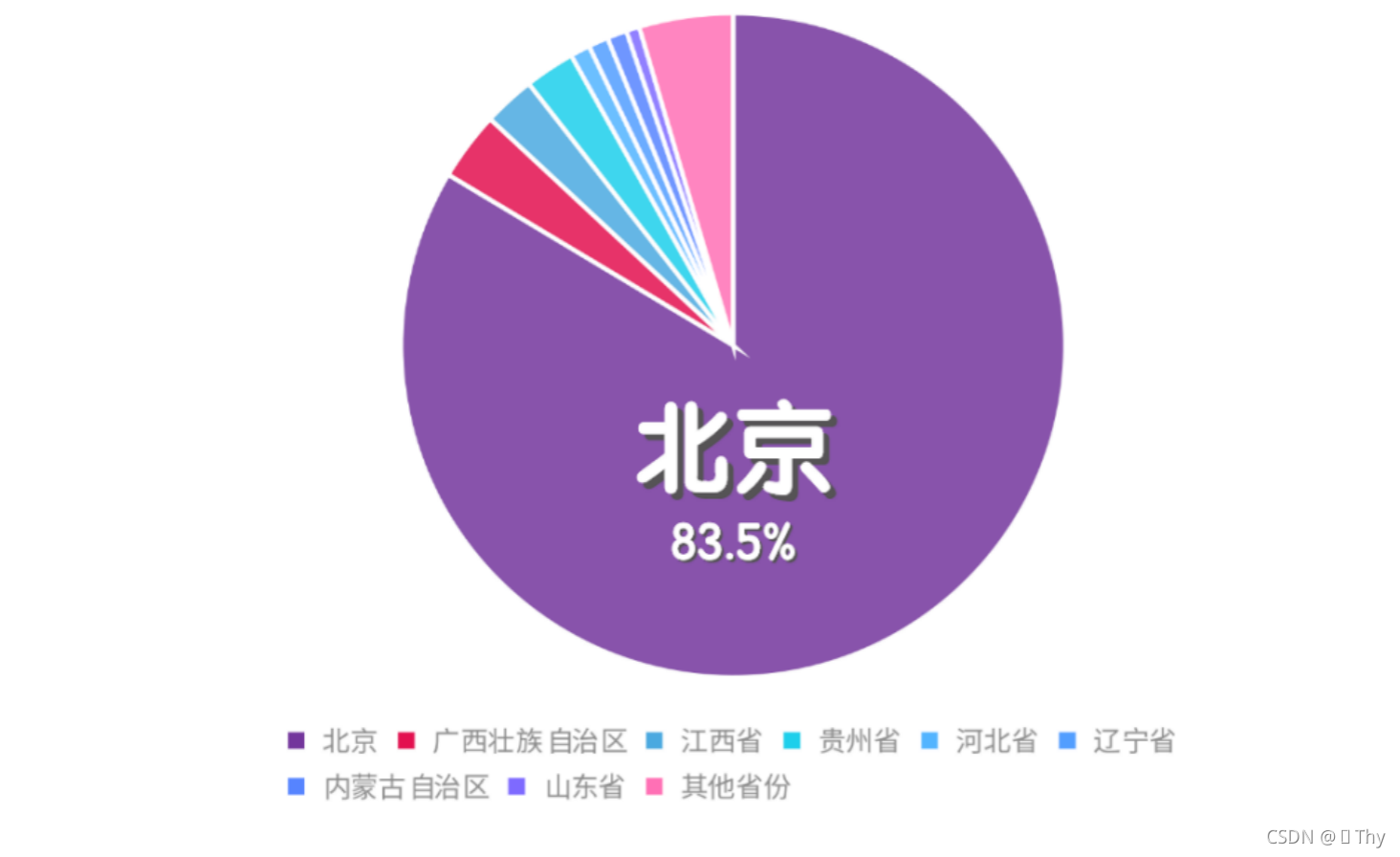
3.3.1 整体城市分布
在全部的1554位受访者中,有1299位均居住在北京,达到83.5%的高占比,符合本次调查的预期要求。和北京受访者相比,其他省份的受访者数量很少,其中最高的广西壮族自治区、江西省、贵州省分别有52、39、38位受访者,占比3.3%、2.5%、2.4%。
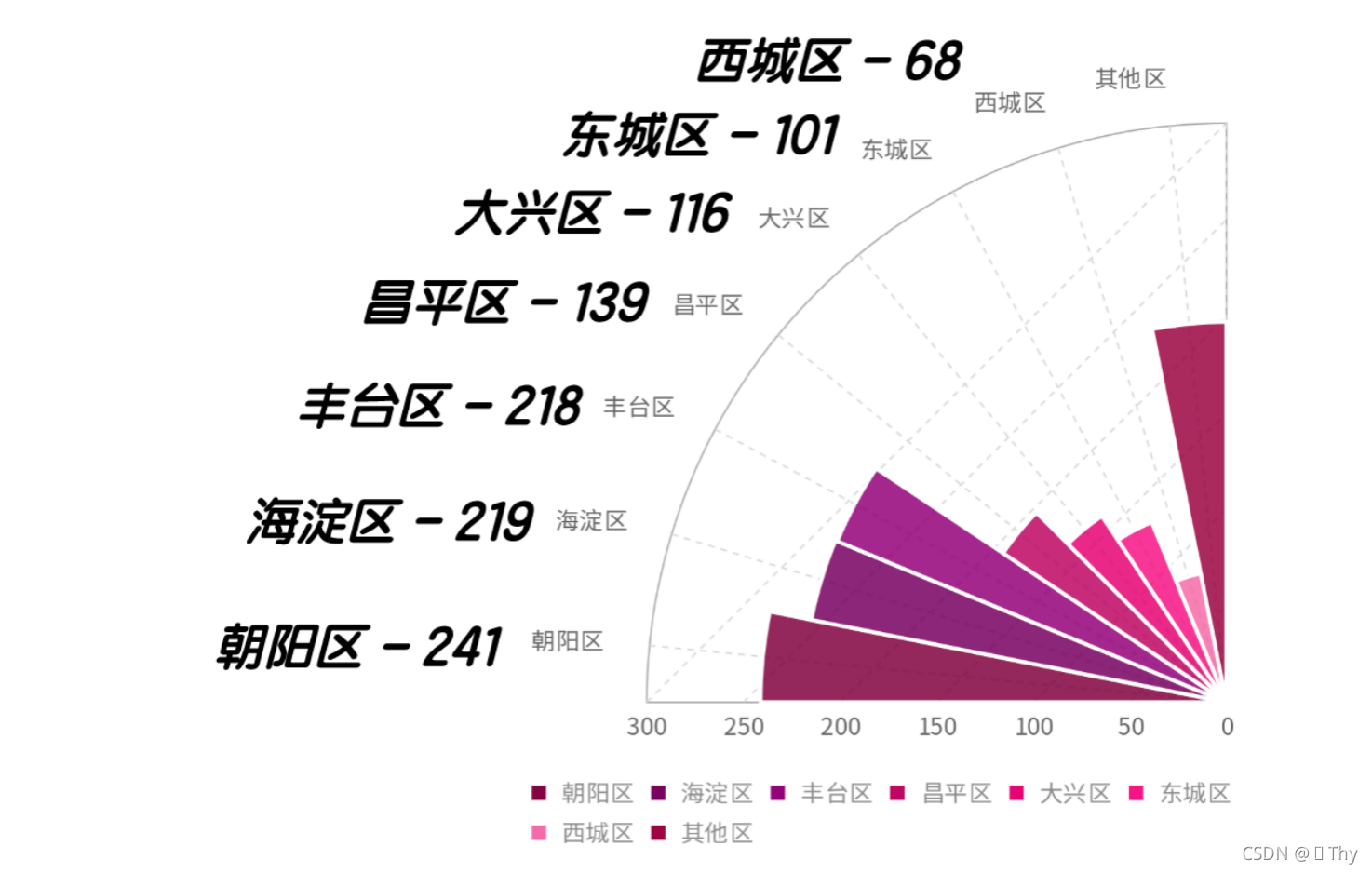
3.3.2 北京市内分布
针对主要面向受访者即北京市居民,进行进一步细分(精确到区),其中主要集中于朝阳区、海淀区、丰台区等区域。
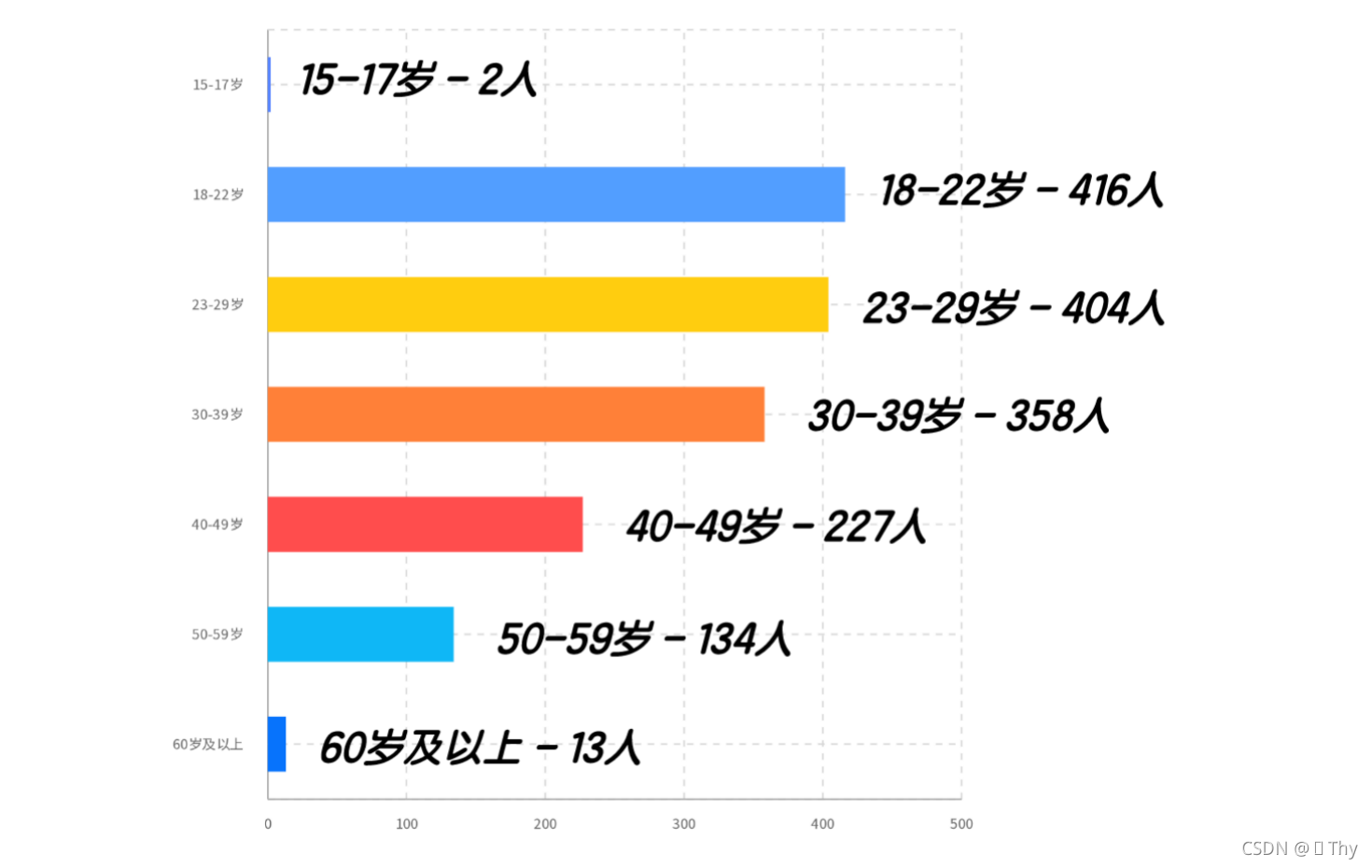
3.4 年龄分布
全部1554位受访者中,除少部分未成年人、少部分60岁及以上老年人外,年龄基本集中于18-59岁,其中18-22岁占比最高,为26.77%;其次,也有较多受访者为23-29岁、30-39岁年龄段,占比分别为26.00%、23.04%。
这个结果显示:最容易受到邀请的是同学们的同龄人,即18-22岁及23-29岁年龄段的民众。除了和同学们具有强社交关系外,这一年龄段的受访者有充足的接受并填写线上问卷的经历和习惯,更愿意接受本次调查。
3.5 工作情况分布
3.5.1 职业情况
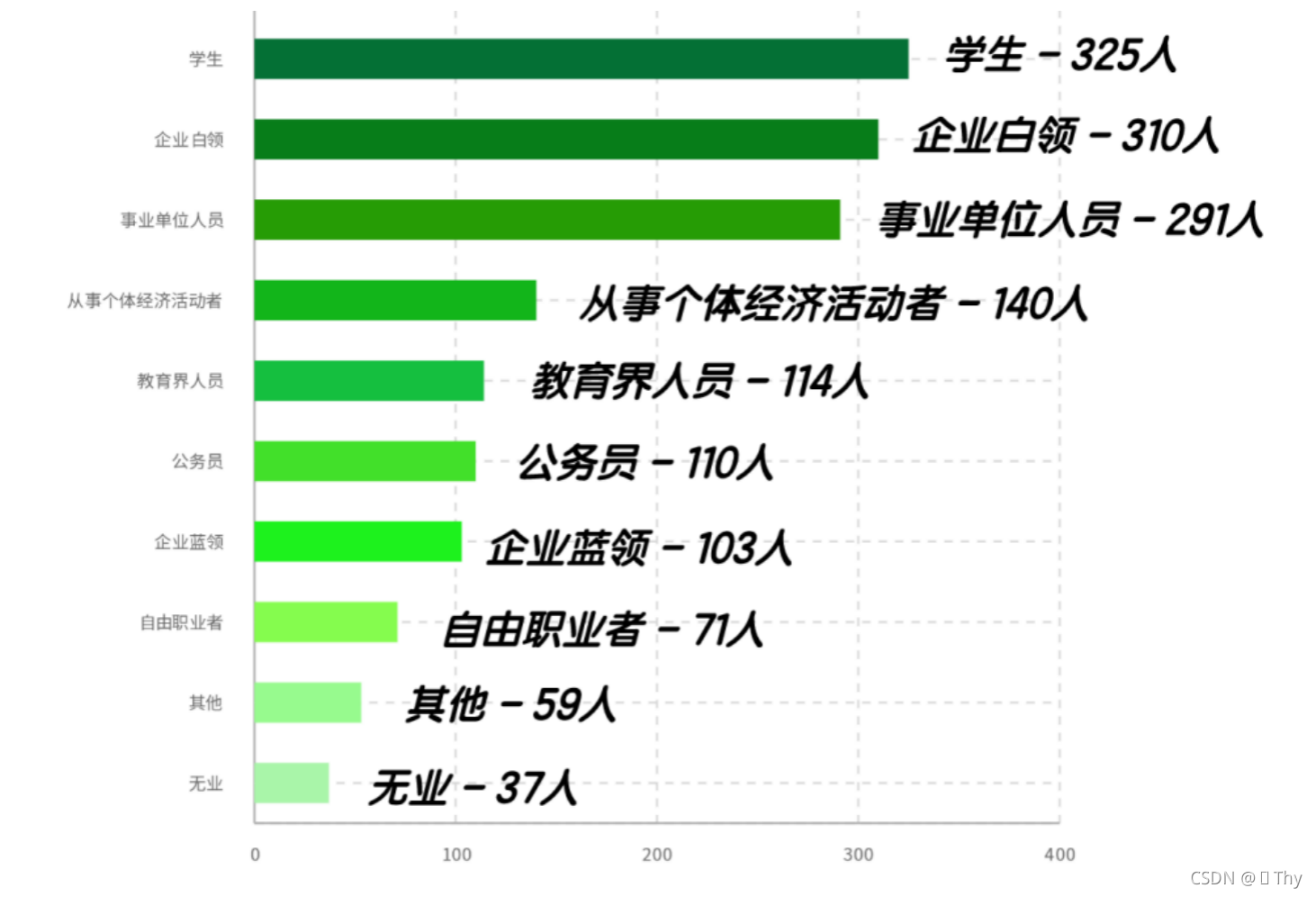
全部1554位受访者中,占比最高的是学生身份,有325人(20.9%);企业白领与事业单位也有较高占比,分别为19.9%、18.7%;从事其他职业类型的受访者相对较少,其中军人、农民、文化文艺出版业等职业占比仅有3.8%。
这个结果与我的预期相符,同学们最容易寻找到的受访者是身边的同学、家长,其中同学的学生身份是最集中、出现频次最高的,因此学生的占比要远高于大部分职业,符合同学们的社交关系。
3.5.2 收入情况
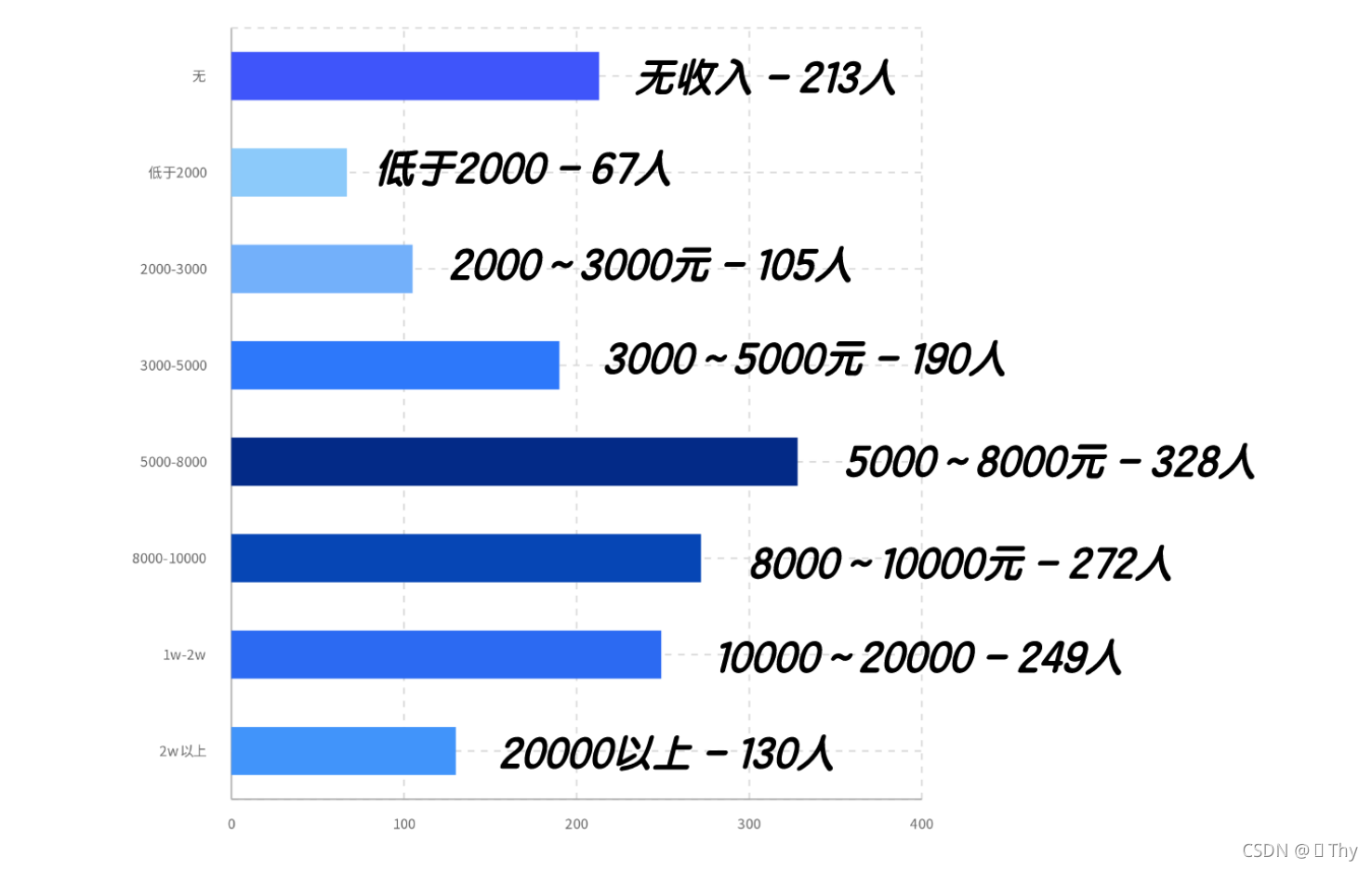
由所有受访者的收入情况,个人每月税后收入范围主要集中于5000元-20000元之间,其中5000元-8000元分段占比最高(21%),有328人均为此收入范围内;也有相当一部分人并无收入,占比为13.6%,推测来自于职业为“学生”或“无业”的受访者。
3.6 学历分布
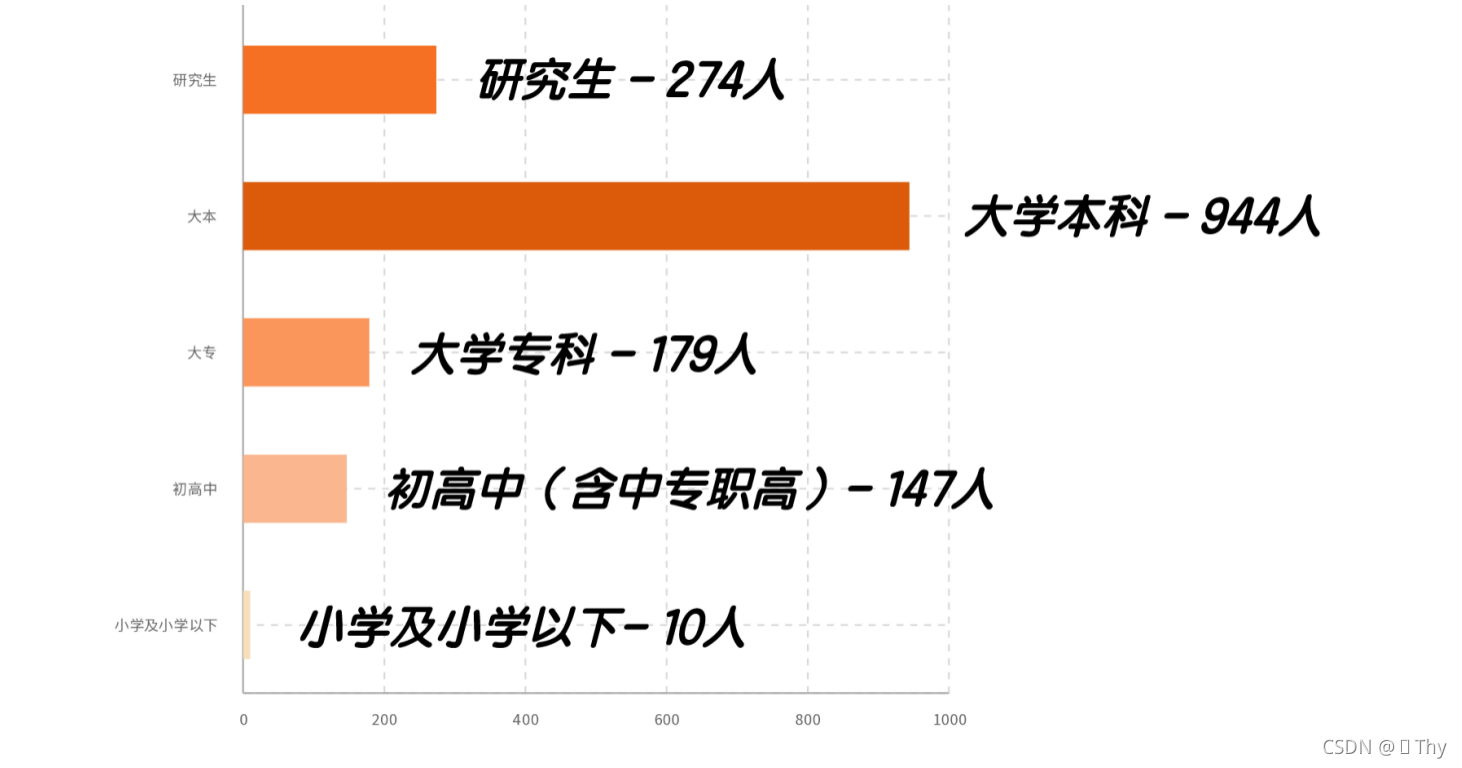
全部1554位受访者中,有60.7%的受访者最高学历均为大学本科;此外也有17.6%的研究生,11.5%的专科生,以及9.4%的中学学历。
4 数据质量判断及处理
4.1 依据IP地址
4.1.1 数据观测
首先我针对IP地址进行频数统计,观察到如下IP地址反复出现了多次:
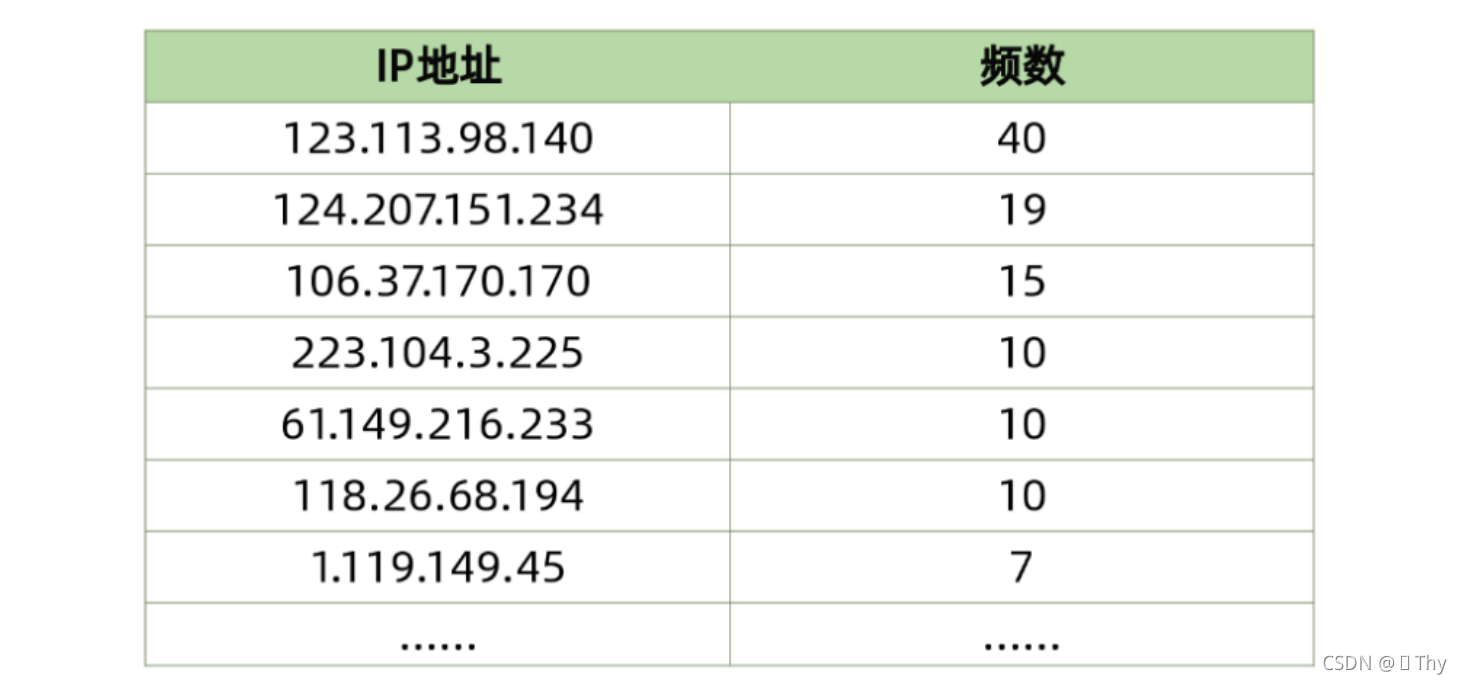
在所有的IP地址中,出现了同一个IP地址反复填写40次的情况,该IP更是在6月30日下午的一个半小时内连续填写25份问卷,具有明显的恶意填写情况,因此相关问卷都应该视作无效。
除此之外,其他多个IP也有反复填写的情况,全部1554份问卷结果中出现了396份问卷由重复IP填写完成,实际仅有1158个不重复的IP地址参与了此次调查。
4.1.2 数据处理
对所有重复填写问卷的IP结果进行处理,仅保留每个IP首次填写问卷作为有效问卷,后续重复填写的问卷数据均不保留。
4.2 依据完成时间
问卷体量较大,正常阅读并完成填写需要一定时间。但在全部问卷结果中,有62份问卷在60秒内即填写完成,显然是无效的。因此将这部分问卷也删除掉。
4.3 依据填写内容
经过上述两次筛选后,仍有一位公务员、一位事业单位人员选择个人每月税后收入为“无”,不符合现实收入情况,即说明这两份问卷出现不根据题目随意选择答案的情况,无法确保答卷可靠性,也不保留。
4.4 数据质量分析结果
在全部的1554份问卷结果中,出现了一部分无效问卷,即上述重复填写IP地址(除首次填写)、完成时间过快、收入与现实不符等问题关联问卷,共计约460份。
去除这些无效问卷后,剩余问卷为1094份。
因此得到有效问卷比例为:70.4%,数据质量为中上等水平。
5 建模分析
5.1 研究问题及目的
我选择研究的是基于受访者对廉政态度的分类问题。针对受访者对廉政的看法进行初步分类,随后使用11种模型分别进行分类操作,得到准确率、混淆矩阵、分类报告、模型耗时,进一步判断出最有利于分析廉政相关问题的模型,以便后续进一步调查及分析工作。
5.2 数据准备
5.2.1 初步分类
将受访者“预防腐败工作及效果”、“非官方机构和个人对腐败的监督情况及效果”、“相信政府会继续保持反腐力度”等认知问题给出的打分进行初步分类,其总分的60%以下为“对廉政治理效果不看好”,60%-75%为“对廉政治理效果感觉一般”,75%-85%为“对廉政治理效果较为看好”,85%以上为“对廉政治理效果很看好”。
5.2.4 热编码
对答卷结果中大量分类变量(针对问卷中的选择题,包括性别、学历等个人信息,以及对各项腐败案件的了解程度等问题)进行热编码,全部替换为0-1型新列。
5.2.3 分割训练集及测试集
将初步分类结果设为Y,其他变量则作为X,在Python中导入后分割训练集及测试集,比例为8:2,随机种子设置为18117(我的年级+学号后3位)。
5.3 模型操作
5.3.1 K近邻

5.3.2 Logistic回归

5.3.3 LDA

5.3.4 QDA
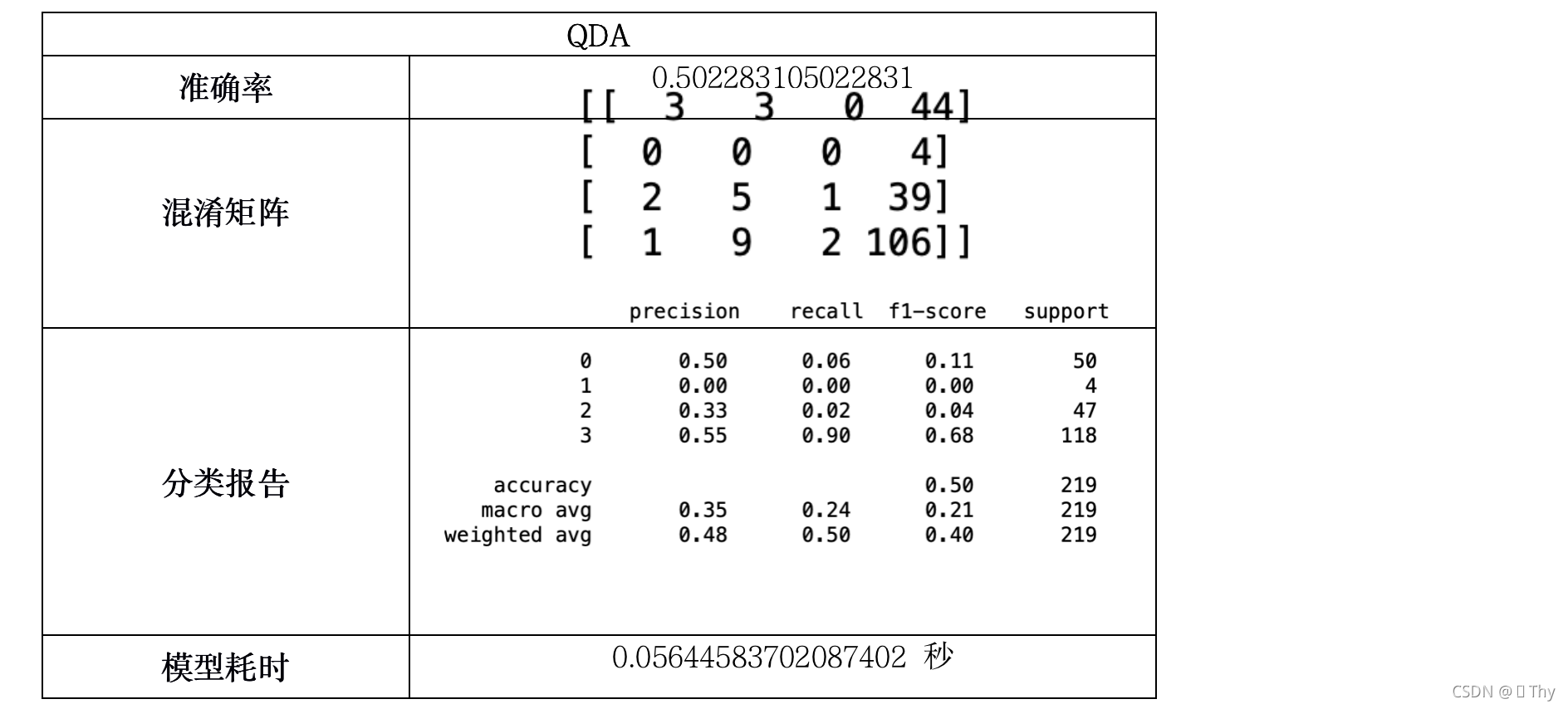
5.3.5 决策树
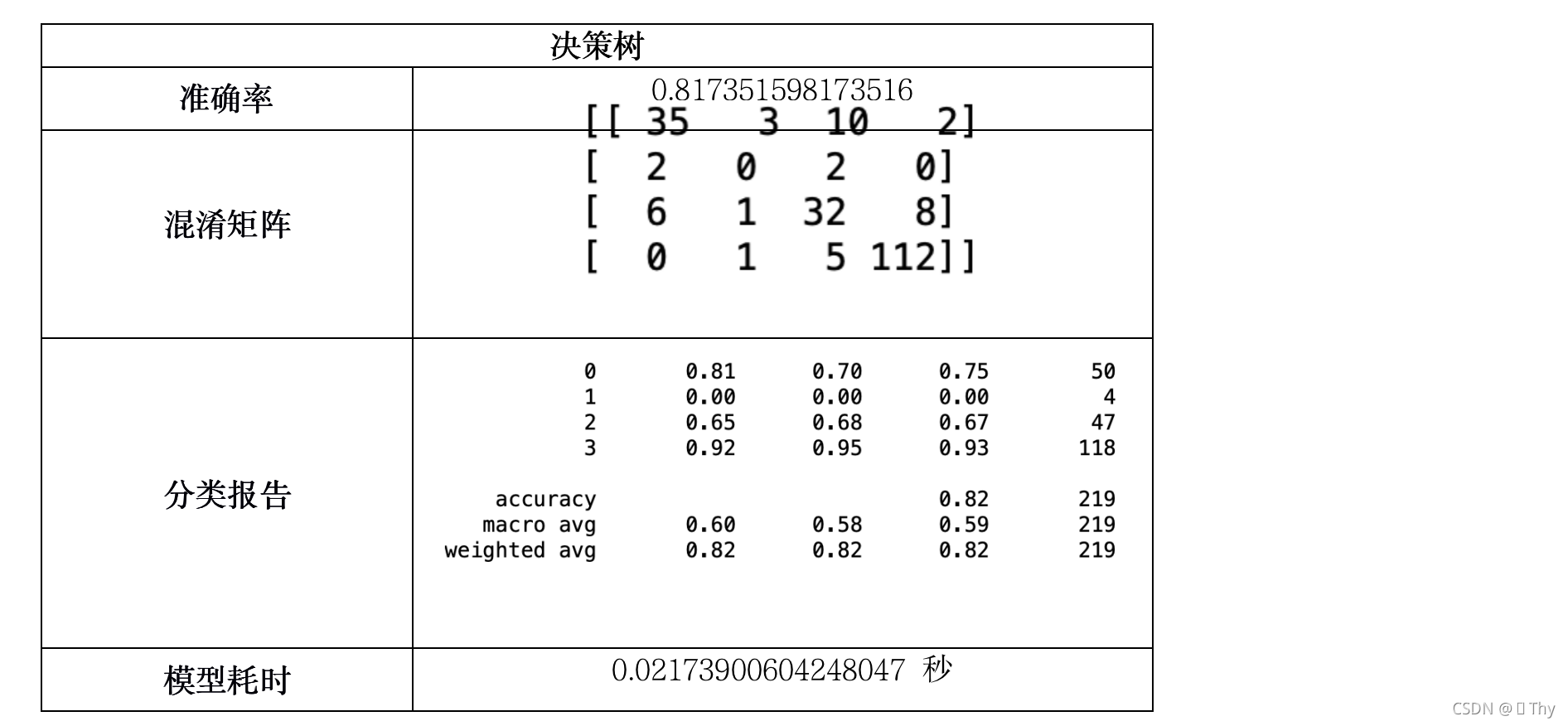
5.3.6 Bagging
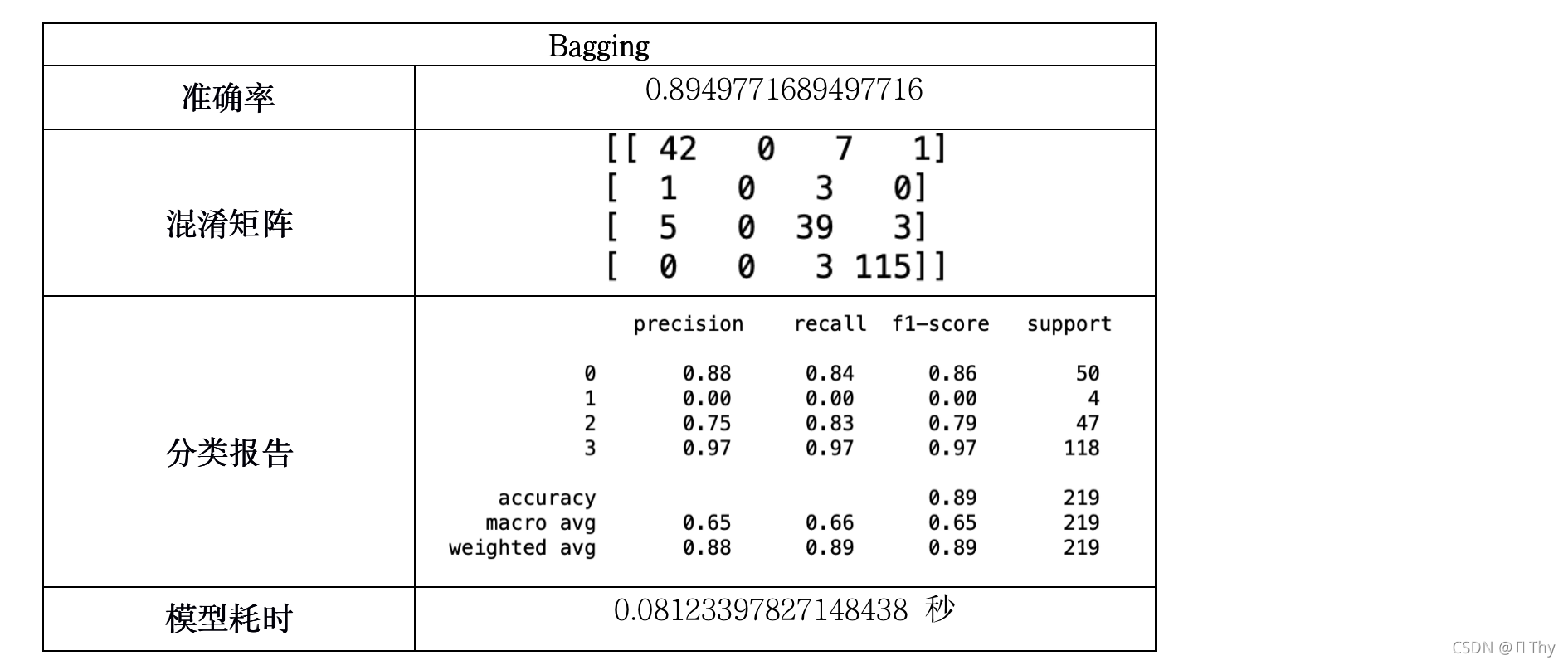
5.3.7 随机森林
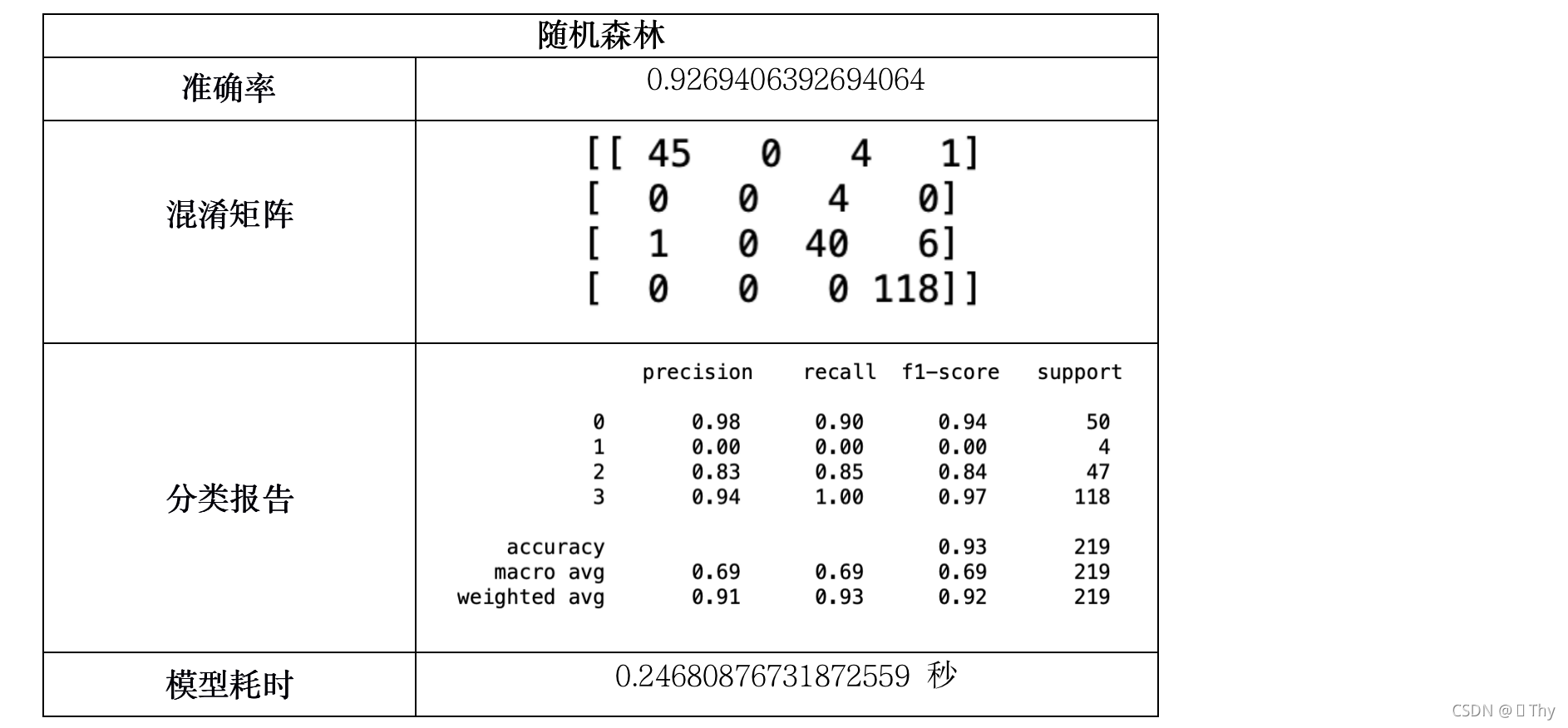
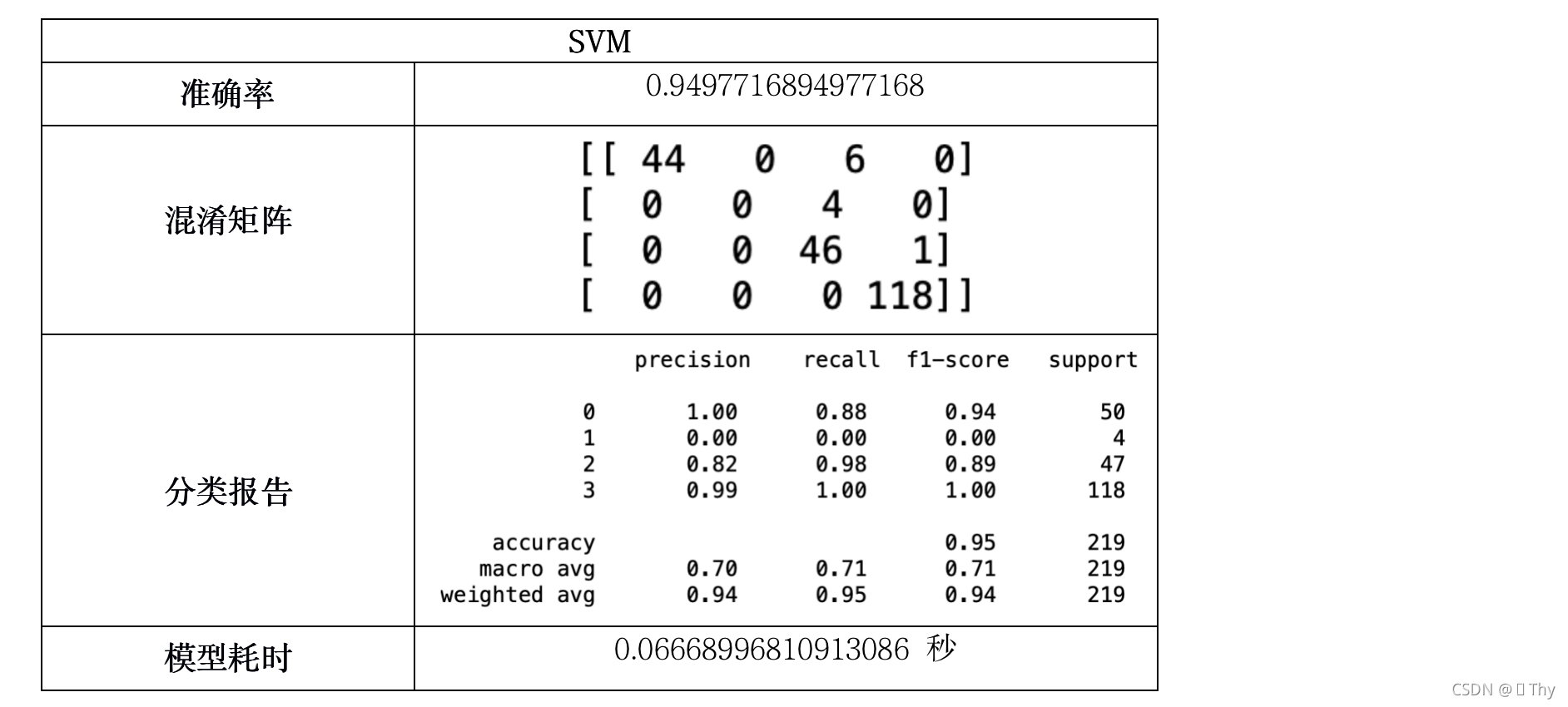
5.3.8 SVM
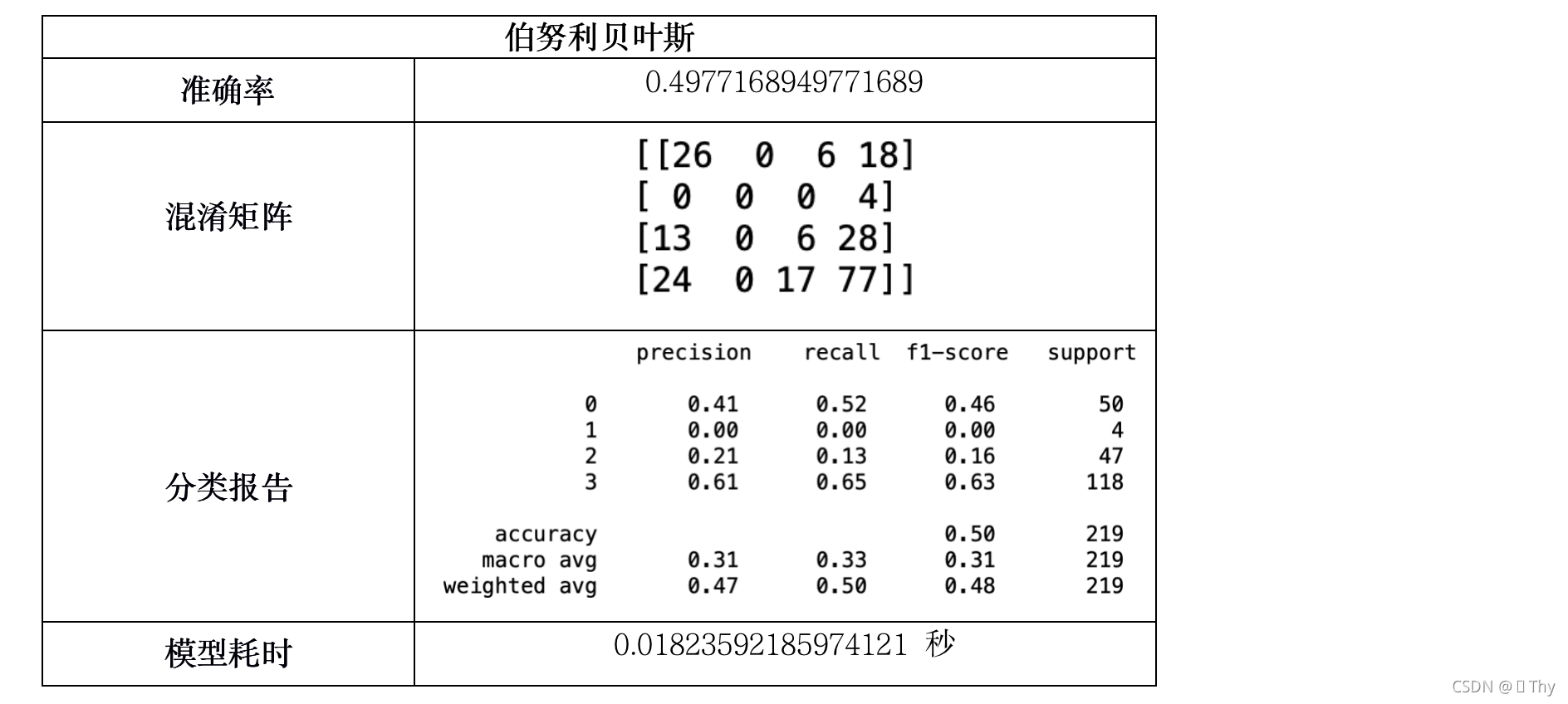
5.3.9 伯努利贝叶斯
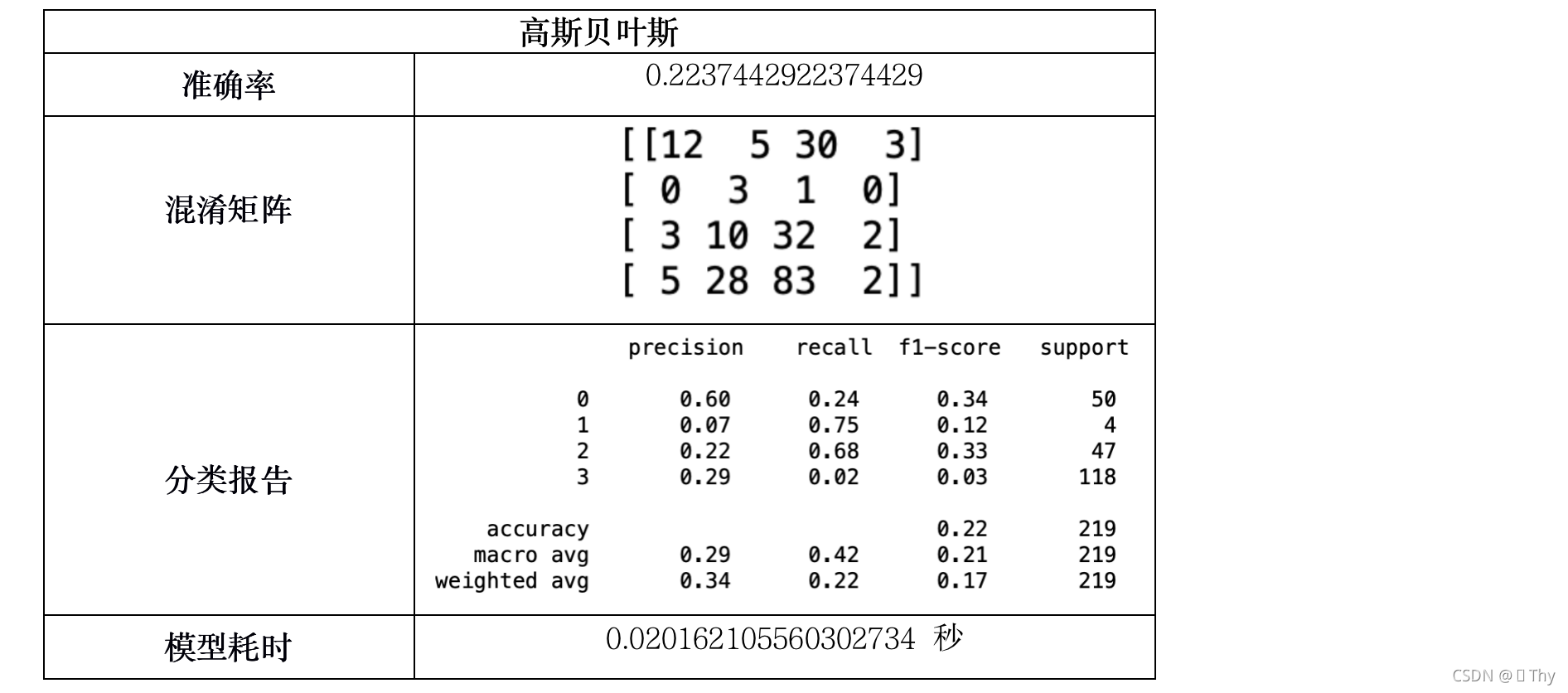
5.3.10 高斯贝叶斯
5.3.11 多项式朴素贝叶斯

5.4 结果分析
由上述11个模型所得结果:除Logistic回归外,其他绝大多数模型耗时均小于1秒,这是因为调查结果样本数量不多,且结构不复杂(不包含矩阵等数据),因此各模型在执行速度上的差异可以忽略不计。
而在准确率方面,QDA、伯努利贝叶斯、高斯贝叶斯、多项式朴素贝叶斯的准确率相对较低,其中高斯贝叶斯甚至仅有22.37%的准确率,而其他模型的准确率均在80%-100%之间,出现如此大的差异是由于模型特性所致。
综合上述,准确率最高的SVM是最适合分析受访者对廉政态度分类问题的模型。
6 问题及建议
6.1 问卷系统改进
在我发放问卷的过程中有几次收到了反馈,受访者填写至一半时不小心滑动屏幕退出了问卷界面,再次点击打开问卷后,问卷系统并没有在线保存问卷实时填写进度。而问卷的体量又比较大,受访者不慎退出后再次进入时,很可能已经没有耐心再次阅读问卷题目内容、填写答案了,这就导致答卷的有效程度产生了一定衰减。
其实现在很多问卷平台已经可以做到保存填写进度,即退出后可以继续之前的答卷进度填写,我的建议是:可以优化问卷系统或更换问卷平台,让受访者在答卷过程中更便捷,进而提高答卷数据质量,同时也有利于同学们指导受访者填写问卷。
6.2 问卷分发方式优化
在疫情背景之下,只能使用线上发送问卷的方式来完成样本的收集。其中不可避免的是:大家都只能找到自己的亲朋好友及其同事们填写问卷,这就导致了样本之间的关联性强,样本来源相对单一,最终在一定程度上影响数据及结果。
我认为可以尝试扩大分发渠道。把握全媒体时代的优势,充分发挥新媒体手段的价值,依托社交媒体平台及相关第三方工具,将问卷的发放对象扩展至个人的关系网络之外。可以尝试的途径有如完成问卷后设置小抽奖、发送小红包;借用相应的奖励对问卷发放产生裂变效果等,将受访人群覆盖面积加大。
附:代码
import pandas as pd
import numpy as np
import scipy
from scipy import io
#分割,比例为8:2,随机数种子设置为18117
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2,random_state = 18117)
#这里需要导入time和metrics,下面会用到
import time
from sklearn import metrics
from sklearn.neighbors import KNeighborsClassifier
model = KNeighborsClassifier()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('K近邻准确率为:', score)
print('\nK近邻混淆矩阵为:\n', matrix)
print('\nK近邻分类报告如下:\n', report)
print('\nK近邻耗时为:', t, '秒\n')
from sklearn.linear_model import LogisticRegression
model = LogisticRegression()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('Logistic回归准确率为:', score)
print('\nLogistic回归混淆矩阵为:\n', matrix)
print('\nLogistic回归分类报告如下:\n', report)
print('\nLogistic回归耗时为:', t, '秒\n')
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
model = LDA()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('LDA准确率为:', score)
print('\nLDA混淆矩阵为:\n', matrix)
print('\nLDA分类报告如下:\n', report)
print('\nLDA耗时为:', t, '秒\n')
from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis as QDA
model = QDA()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('QDA准确率为:', score)
print('\nQDA混淆矩阵为:\n', matrix)
print('\nQDA分类报告如下:\n', report)
print('\nQDA耗时为:', t, '秒\n')
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('决策树准确率为:', score)
print('\n决策树混淆矩阵为:\n', matrix)
print('\n决策树分类报告如下:\n', report)
print('\n决策树耗时为:', t, '秒\n')
from sklearn.ensemble import BaggingClassifier
model = BaggingClassifier()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('Bagging准确率为:', score)
print('\nBagging混淆矩阵为:\n', matrix)
print('\nBagging分类报告如下:\n', report)
print('\nBagging耗时为:', t, '秒\n')
from sklearn.ensemble import RandomForestClassifier
model = RandomForestClassifier()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('随机森林准确率为:', score)
print('\n随机森林混淆矩阵为:\n', matrix)
print('\n随机森林分类报告如下:\n', report)
print('\n随机森林耗时为:', t, '秒\n')
from sklearn import svm
model = svm.SVC()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('SVM准确率为:', score)
print('\nSVM混淆矩阵为:\n', matrix)
print('\nSVM分类报告如下:\n', report)
print('\nSVM耗时为:', t, '秒\n')
from sklearn.naive_bayes import BernoulliNB
model = BernoulliNB()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('伯努利贝叶斯准确率为:', score)
print('\n伯努利贝叶斯混淆矩阵为:\n', matrix)
print('\n伯努利贝叶斯分类报告如下:\n', report)
print('\n伯努利贝叶斯耗时为:', t, '秒\n')
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('高斯贝叶斯准确率为:', score)
print('\n高斯贝叶斯混淆矩阵为:\n', matrix)
print('\n高斯贝叶斯分类报告如下:\n', report)
print('\n高斯贝叶斯耗时为:', t, '秒\n')
from sklearn.naive_bayes import MultinomialNB
model = MultinomialNB()
start = time.time()
model.fit(X_train, Y_train)
Y_pred_model = model.predict(X_test)
score = metrics.accuracy_score(Y_test, Y_pred_model)
matrix = metrics.confusion_matrix(Y_test, Y_pred_model)
report = metrics.classification_report(Y_test, Y_pred_model)
end = time.time()
t = end - start
print('多项式朴素贝叶斯准确率为:', score)
print('\n多项式朴素贝叶斯混淆矩阵为:\n', matrix)
print('\n多项式朴素贝叶斯分类报告如下:\n', report)
print('\n多项式朴素贝叶斯耗时为:', t, '秒\n')