[人工智能]强化学习 - Importance Sampling

知识准备

假设随机变量X的取值：$x_1,x_2,...,x_n$，它对应的概率$P$是：$p_1,p_2,...,p_n$，则关于$X_i$的数学期望是：
$$E(X)=\sum _{k=1}^{\infty }{x}_i{p}_k$$
如果$h(x_i)$是关于随机变量$X$的事件，则它发生的概率跟随机变量$X$一样，所以$h$的数学期望是：
$$E(h)=\sum _{k=1}^{\infty }h(x_k)p_k$$
如果随机变量$X$是连续的，它的概率密度函数为$f(x)$，则$X$的数学期望是：
$$E(X)={\int }_{?\infty }^{\infty }xf(x)dx$$
同理关于连续随机变量$X$的事件$h(x)$的数学期望是：
$$E(X)={\int }_{?\infty }^{\infty }h(x)f(x)dx$$
在实际应用中，我们一般通过对$X$进行采样，来近似上面的积分。但是有时候在样本点中有很大一部分会使得函数$h(x)$趋向于0，说明这些样本的“贡献”太小。这时就需要优化采样的方法，让样本大多是“关键”样本。例如：重要度采样方法（Importance Sampling）。此外如果样本不那么容易采集到的话，也可以使用这个方法。

重要度采样的逻辑在于目标积分中项的简单重新排列
$$\begin{array}{rl}E(h)& =\int h(x)p(x)dx\\ & =\int h(x)\frac{p(x)}{g(x)}g(x)dx\\ & =\int h(x)w(x)g(x)dx\end{array}$$
$g(x)$是另外一个概率密度函数，它与$p(x)$的采样空间是一样的。$w(x)$被称为重要度函数（importance function），理想情况下如果被积函数$h(x)$的值很大，则$w(x)$也会很大，反之则很小。

降低积分近似的方差

重要度采样方法是如何降低积分近似的方差的？
假设函数$h(x)=e^{?2?|x?5|}$,我们需要计算它的数学期望$E(h)$，其中$X$~Uniform(0,1)（平均分布），也就是要计
$${\int }_0^{10}10?e^{?2?|x?5|}?\frac{1}{10}dx$$
Solution 1：简单的做法是从Uniform(0,10)的分布中采样，然后计算$10?h(x_i)$的均值。

import numpy as np
def f(x):
    return 10*np.exp(-2*np.abs(x-5))
if __name__ == '__main__':
    x = np.random.uniform(0,10,100000)
    y = f(x)
    print(np.mean(y)) #均值
    print(np.var(y)) #方差
    
#均值：0.9887775224871374
#方差：3.9421223842069995

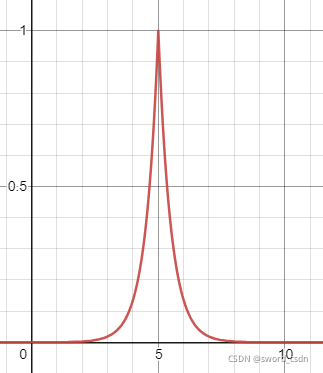
函数$h$在$x=5$的位置达到高峰，总体呈现比较狭长的形状。在均匀分布下，面对这样的函数，所采集的样本对期望的贡献很小。所以我们需要一个新的采样分布，让采集到的样本更多的集中在5附近（之前的分布采样比较分散）。

Solution 2：可以换一种思路，将上面的积分公式重写为：
$$\begin{array}{rl}{\int }_0^{10}10?e^{?2?|x?5|}?\frac{1}{10}dx& ={\int }_0^{10}10?e^{?2?|x?5|}?\frac{1}{10}?\frac{1}{\frac{1}{\sqrt{2\pi }}?e^{?(x?5{)}^2}}?\frac{1}{\sqrt{2\pi }}?e^{?(x?5{)}^2}dx\\ & \\ & ={\int }_0^{10}{e}^{?2|x?5|}\sqrt{2\pi }{e}^{(x?5{)}^2/2}?\frac{1}{\sqrt{2\pi }}{e}^{?(x?5{)}^2/2}dx\end{array}$$
也就是，$E(h(X)w(X)),X～N(5,1)$
当$p(x)=1/10$时，$g(x)$是$N(5,1)$（正态分布概率密度函数），$w(x)=\frac{\sqrt{2\pi }{e}^{(x?5{)}^2}/2}{10}$是重要度函数。

import numpy as np


def f(x):
    return 10*np.exp(-2*np.abs(x-5))

def w(x):
    return np.sqrt(2*np.pi)*np.exp((x-5)**2/2)/10


if __name__ == '__main__':

    x = np.random.normal(5,1,100000)
    h = f(x)
    w = w(x)

    print(np.mean(w*h))
    print(np.var(w*h))

#均值：0.9995183992557544
#方差：0.36046391025704455

Conclusion：使用重要度采样可以有效降低积分估计的方差，solution 2是solution 1的1/10，而solution 1恰好是简单MC算法的采样方法。

当无法从原概率密度函数采样时…

假设有一个无法从中采样的分布概率密度函数（Probability Density Function,PDF）：
$$p(x)=\frac{1}{2}{e}^{?|x|}$$
这个函数被称作双指数概率密度函数，它的累积分布函数（Cumulative Distribution Function，CDF）是：
$$F(x)=\frac{1}{2}{e}^x\tau (x\le 0)+(1?e^{?x}/2)\tau (x>0)$$
它非常难以计算和转换。现在需要基于这个PDF计算$h(x)=x^2$的数学期望。所以我们需要计算积分：
$${\int }_{?\infty }^{\infty }{x}^2\frac{1}{2}{e}^{?|x|}dx$$
由于没法从原密度函数中采样，所以我们可以将其改写为：

$${\int }_{?\infty }^{\infty }{x}^2\frac{\frac{1}{2}{e}^{?|x|}}{\frac{1}{\sqrt{8\pi }}{e}^{?x^2/8}}?\frac{1}{\sqrt{8\pi }}{e}^{?x^2/8}dx$$
其中$\frac{1}{\sqrt{8\pi }}{e}^{?x^2/8}$是$N(0,4)$的正态概率密度函数。

import numpy as np


def h(x):
    return x**2

def w(x):
    return (0.5*np.exp(-np.abs(x)))/((np.exp((-x**2)/8))/np.sqrt(8*np.pi))


if __name__ == '__main__':

    x = np.random.normal(0,2,100000)
    h = h(x)
    w = w(x)

    print(np.mean(w*h))

#均值：1.981319010462215

这个积分的真实值是2，所以通过重要度采样的结果是非常接近的。