1.实验背景与问题提出
????????聚类(clustering)是无监督学习(unsuperviserd learning)中研究和应用最多的一类学习算法,目的是将样本划分成若干个“簇”(cluster),每个“簇”之间尽量相异,每个簇之内的样本尽量相似。K-Means假设聚类结构能够通过一组原型(点)刻画,K-Means中的原型是指每个“簇”的质心,这个原型可以使得“簇”内的平方误差的加和达到最小,公式如下:
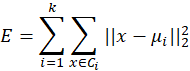
????????K-Means算法的目标是最小化聚类后“类”内的平方误差和,因为E值越小,“类”内的样本相似性越高。但是这个最小化过程是NP难问题,没有有效的算法,只能遍历所有可能的组合(“类”),当样本量较大时就是非常浪费资源甚至无解的。所以考虑使用贪心算法,即通过迭代优化来求近似解。
????????获得安全饮用水对健康至关重要,是一项基本人权,也是有效的健康保护政策的组成部分。在国家、区域和地方各级,这是一个重要的健康和发展问题。本次实验数据来源于Kaggle官网中的一个Water Quality dataset。原始数据集中有3276个样本,10个属性:ph, Hardness(硬度), Solids(总溶解固体量), Chloramines(氯胺含量), Sulfate(硫酸盐含量), Conductivity(电导率), Organic_carbon(有机碳含量), Trihalomethanes(三卤甲烷含量), Turbidity(浊度), Potability(可饮用性),数据全为float或者int类型,Potability为只取0或1的标签,表示检测的水是否可饮用。本次实验旨在用Water Quality dataset训练KMeans模型,通过训练的模型实现对水质样本的分类。
2、解决思路
2.1 数据预处理
????????首先读取数据,查看数据的基本信息,发现多数列都存在空值,于是对空值进行删除。
 ??
?? 
2.2 聚类数K值选取
????????K-Means算法是聚类中的基础算法,也是无监督学习里的一个重要方法。其基本原理是随机确定k(人为指定)个初始点作为簇质心,然后将数据样本中的每一个点与每个簇质心计算距离,依据此距离对样本进行分配;之后将每次簇的质心更改为该簇内所有点的平均值。普通的K-Means算法因为初始簇质心的随机性,很可能会收敛到局部最优。为解决这一情况,可以随机初始化若干次,取最好结果,但这种方法在初始给定K值较大的情况下,可能只会得到比前一次好一点的结果(因为K值越大,簇质心越多,则随机性带来的不确定性越小。)
????????那么如何选取较为合适的K值呢?查阅资料,找到一种度量方法:各个簇内的样本点到所在簇质心的距离平方和(SSE),SSE越小则说明各个类簇越收敛。但并不是SSE越小越好,因为一种极端情况时将所有的样本点均视作簇,这样的话SSE为0,显然达不到分类的效果。我们要做的就是在类簇数量与SSE之间寻求一个平衡点。肘部法则为我们提供了这样的方法。肘部法则核心思想:随着聚类数K的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。并且,当K小于真实聚类数时,由于K的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大,而当K到达真实聚类数时,再增加K所得到的聚合程度回报会迅速变小,所以SSE的下降幅度会骤减,然后随着K值的继续增大而趋于平缓,也就是说SSE和k的关系图是一个手肘的形状,而这个肘部对应的K值就是数据的真实聚类数。手肘法即为选取那个拐点。
(原文链接:
分析kMeans、二分K-Means算法及肘部法则_Starbeing的博客-CSDN博客_肘部法则)


图2 数据SSE-K图
????????观察上图可以发现经过数据标准化后,SSE-K图像的拐点并不明显,因此选择没有标准化的数据来确定K值,由图2左边可以看到拐点为K=2。
2.3 数据建模可视化
????????选择K=2,由于除标签外有9个属性,是不能可视化的。于是想到利用PCA降维降到2维后进行可视化,首先调用PCA得到降维数据,接着利用降维数据调用sklearn.cluste库中的KMeans模型进行聚类,最后通过python画图库对聚类效果可视化,得到了图4的结果。
?????? 由于结果并不理想,于是选择原始数据进行聚类,利用聚类标签与真是标签不同样本所占百分比来评价聚类效果的好坏,但是结果并不理想。于是更改数据集,最后得到较好的聚类结果。
3、算法步骤
输入:样本集
step1: 随机选择K个点作为初始原型;
step2: 计算剩余的点到K个点的距离,将点划入距离最近的原型所在的“簇”内;
step3: 计算每个“簇”点的均值,并将每个“簇”的均值更新为新的原型;
step4: 重复前面3步,直到每个“簇”点的均值不再变化;
step5: 输出每个"簇"的中心。
输出:训练好的K-Means模型。
为避免运行时间过长,通常会设置一个最大的迭代轮次或者设置最小调整幅度阀值。
实验步骤:

图3 实验步骤流程图
4、结果分析
?????? 利用PCA将数据降到2维后,得到图4的结果。蓝色和红色表示聚类分出来的两个类,可视化发现结果并不好,于是不对数据降维,利用K-means聚类给数据贴上类别标签,接着与真是标签对比。发现聚类打上的标签与实际标签结果相差很大,有47.1436%的误差,这类似于随机聚类的效果。探究问题原因:难道是因为属性间的相关度不高吗?于是从结果去探究出现这个问题的原因,进行了以下三种探究:
探究1绘制热力图,很明显从图5中可以看到,属性与决策属性Potability间的相关性很低,甚至没有其他属性与Solids的总相关度高。
探究2:用此数据集利用决策树算法分类,发现在测试集占比20%的情况下分类准确率只有63.02%。
探究3:图6是用k-means聚类的效果,图7是原始数据分布图,是用于Potability相关度最高的两个属性:Solids和Sulfate绘制得散点图,发现数据分布是杂乱无章的,用肉眼几乎看不出有明显的边界。
综上所述,这个数据集并不适合做聚类(即使是分类也不适合,因为所给的属性能作为分类的有效信息很少)。
 ??
?? 
图4 降维后聚类与实际标签结果? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 图5 热力图
 ??
??
图6 不降维聚类标签Solids-Sulfate图? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 图7 实际标签Solids-Sulfate图
?????? 更换数据:重新选取了一个属性间相关度较高的数据集:Blood Transfusion Service Center Data Set,删除完空白行后一共有748个样本,5个属性,其中donated blood in 2007是标签(官网解释是:是否在2007年献血)。查看属性相关度发现有两个属性是线性相关的,因此删除。依据SSE-K图选择K=2。接着训练模型,图10和图11分别是原始数据两类样本的分布情况和K-Means聚类后两类样本的分布情况,用excel计算得到二者标签重合率为72.32%,表1是真实标签和K-means聚类标签的对比情况。这个数据集的表现要优于开始选取的水质数据集。
 ??
?? 
图8 热力图 ????????????????????????????????????图9 SSE-K图
 ?
?
图10原始数据分布 ?????????????????????图11 K-Means聚类数据分布
表1 原始标签和K-means标签对比情况
| Recency | Frequency | Monetary | Time | donated blood in 2007 | predict |
| 21 | 2 | 500 | 52 | 0 | 0 |
| 23 | 3 | 750 | 62 | 0 | 0 |
| 39 | 1 | 250 | 39 | 0 | 0 |
| 72 | 1 | 250 | 72 | 0 | 0 |
| 2 | 50 | 12500 | 98 | 1 | 1 |
| 0 | 13 | 3250 | 28 | 1 | 1 |
| 1 | 16 | 4000 | 35 | 1 | 1 |
| 2 | 20 | 5000 | 45 | 1 | 1 |
| 2 | 7 | 1750 | 14 | 1 | 0 |
| 2 | 9 | 2250 | 22 | 1 | 0 |
5、实验核心代码
#绘制肘点图
loss = []
for i in range(1, 10):
??? kmeans = KMeans(n_clusters=i, max_iter=100).fit(X_train)
loss.append(kmeans.inertia_ / point_number)???? #kmeans.inertia_ 是样本到其最近聚类中心之和
plt.plot(range(1, 10), loss,c='lime',marker="v" )
plt.show()
#降维并对降维数据聚类、绘制可视化图像
from sklearn.decomposition import PCA
reduced_data = PCA(n_components=2).fit_transform(sd_df)
kmeans = KMeans(n_clusters=2)#
kmeans.fit(reduced_data)
DF=pd.DataFrame(columns=["0","1","Y"])
DF[["0"]]=pd.DataFrame(reduced_data[:, 0])
DF[["1"]]=pd.DataFrame(reduced_data[:, 1])
DF[["Y"]]=Y
Y=df.iloc[:,a_number-1]
Y.reset_index(drop=True)
plt.figure(figsize=(12,12))
h = 0.02? # point in the mesh [x_min, x_max]x[y_min, y_max].
x_min, x_max = reduced_data[:, 0].min() - 1, reduced_data[:, 0].max() + 1
y_min, y_max = reduced_data[:, 1].min() - 1, reduced_data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Obtain labels for each point in mesh. Use last trained model.
Z = kmeans.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
#plt.figure(1)
plt.clf()
plt.imshow(
??? Z,
??? interpolation="nearest",
??? extent=(xx.min(), xx.max(), yy.min(), yy.max()),
??? cmap=plt.cm.Paired,
??? aspect="auto",
??? origin="lower",
)
#plt.plot(reduced_data[:, 0], reduced_data[:, 1], "k.", markersize=4)
sns.scatterplot(data=DF, x="0", y="1", hue="Y")
# Plot the centroids as a white X
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1], marker="x",s=169, linewidths=3, color="w",
zorder=10,)
plt.title("K-means clustering on the digits dataset (PCA-reduced data)\n"
??? "Centroids are marked with white cross",fontproperties=myfont)
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.xticks(())
plt.yticks(())
plt.legend(fontsize=20)
plt.show()
#matlabe绘制三维散点图代码
a=csvread(".\predict2.csv");
x1=a(1:570,1);
y1=a(1:570,2);
z1=a(1:570,4);
x2=a(1:748,1);
y2=a(1:748,2);
z2=a(1:748,4);
c=a(:,6)*10;
figure
scatter3(x2,y2,z2,20,c);
xlabel('Recency (months)');ylabel('Frequency (times)');zlabel('Time (months)')五、实验总结
- 不适合圆环形状的簇、不适合交错分布没有明显界限的簇、不适合大小差别较大的簇。
- 对噪声和异常点比较敏感。
- 初始值的选取会影响最终聚类效果。
- 聚类数量K很重要,K值可以通过绘制SSE图观察肘点得到。在绘制SSE图时不对数据归一化处理会比归一化处理后的肘点更加明显。
- K-Means不适用于类似圆形的数据集,聚类效果很差,主要是算法的原因。
- 要想得到好的结果,选择合适的数据集至关重要,如果不能提供足够的信息去分类或者做决策,那么模型的效果一定是不好的,属性携带的信息就好像“米”,巧妇难为无米之炊,没有足够的原材料,添加再多的作料也无济于事。
- 在选取数据时先查看属性之间的相关程度。
- K-Means是用来做无标签学习的,它能从数据中提取信息然后按照最小化SSE来对数据聚类,这种原理不一定是贴合实际的,因为事物分类的情况有很多种,并不是简单的距离越小就是一个类别,因此将K-Means聚类标签和原始标签去对比在一定程度上重合度不会特别高,而本次实验最终得到了72.32%已经是一个不错的效果。
- 在没有标签的情况下可以用K-Means对数据进行标记。