[人工智能]sklearn实战06：xgboost

1 梯度提升树

class xgboost.XGBRegressor (max_depth=3, learning_rate=0.1, n_estimators=100, silent=True,objective='reg:linear', booster='gbtree', n_jobs=1, nthread=None, gamma=0, min_child_weight=1, max_delta_step=0,subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1, scale_pos_weight=1,base_score=0.5, random_state=0, seed=None, missing=None, importance_type='gain', **kwargs)

1.1 重要参数：n_estimators

对于梯度提升树来说，每个样本的预测结果表示为所有树上结果的加权求和：

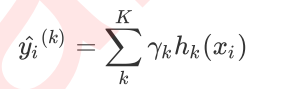
其中，K是树的总数量，k代表第k棵树，γk是这棵树的权重，hk表示这棵树上的预测结果。
而对于XGB来说，每个叶子节点上会有一个预测分数（prediction score），也被称为叶子权重。这个叶子权重就是所有在这个叶子节点上的样本在这一棵树上的回归取值，用fk(xi)或者w来表示，其中fk表示第k棵决策树，xi表示样本i对应的特征向量。当只有一棵树的时候，f1(xi)就是提升集成算法返回的结果，但这个结果往往非常糟糕。当有多棵树的时候，集成模型的回归结果就是所有树的预测分数之和，假设这个集成模型中总共有K棵决策树，则整个模型在这个样本i上给出的预测结果为：

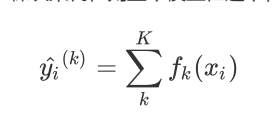
因此我们要做的第一件事是确定K，即建几棵树。

from xgboost import XGBRegressor as XGBR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.linear_model import LinearRegression as LinearR
from sklearn.datasets import load_boston
from sklearn.model_selection import KFold, cross_val_score as CVS, train_test_split as TTS
from sklearn.metrics import mean_squared_error as MSE
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from time import time
import datetime
data = load_boston()
X = data.data
y = data.target

-------定义绘制以训练样本数为横坐标的学习曲线的函数-----------------
def plot_learning_curve(estimator,title, X, y, 
                        ax=None, #选择子图
                        ylim=None, #设置纵坐标的取值范围
                        cv=None, #交叉验证
                        n_jobs=None #设定索要使用的线程
                       ):
    
    from sklearn.model_selection import learning_curve
    import matplotlib.pyplot as plt
    import numpy as np
    
    train_sizes, train_scores, test_scores = learning_curve(estimator, X, y
                                                            ,shuffle=True
                                                            ,cv=cv
                                                            ,random_state=420
                                                            ,n_jobs=n_jobs)      
    if ax == None:
        ax = plt.gca()
    else:
        ax = plt.figure()
    ax.set_title(title)
    if ylim is not None:
        ax.set_ylim(*ylim)
    ax.set_xlabel("Training examples")
    ax.set_ylabel("Score")
    ax.grid() #绘制网格，不是必须
    ax.plot(train_sizes, np.mean(train_scores, axis=1), 'o-'
            , color="r",label="Training score")
    ax.plot(train_sizes, np.mean(test_scores, axis=1), 'o-'
            , color="g",label="Test score")
    ax.legend(loc="best")
    return ax
    
---------------使用参数学习曲线观察n_estimators对模型的影响---------------
axisx = range(10,1010,50)
rs = []
for i in axisx:
    reg = XGBR(n_estimators=i,random_state=420)
    rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()

-----------------进化的学习曲线：方差与泛化误差---------------------------
axisx = range(50,1050,50)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=i,random_state=420)
    cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
    #记录1-偏差
    rs.append(cvresult.mean())
    #记录方差
    var.append(cvresult.var())
    #计算泛化误差的可控部分
    ge.append((1 - cvresult.mean())**2+cvresult.var())
#打印R2最高所对应的参数取值，并打印这个参数下的方差
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
#打印方差最低时对应的参数取值，并打印这个参数下的R2
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
#打印泛化误差可控部分的参数取值，并打印这个参数下的R2，方差以及泛化误差的可控部分
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="red",label="XGB")
plt.legend()
plt.show()

因为这里我们的数据量少，模型相对不稳定，因此需要把方差也纳入考虑的范围。因此需要改进学习曲线

-------------细化学习曲线，找到最佳的n_estimators-----------------
xisx = range(100,300,10)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=i,random_state=420)
    cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)*0.01
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
#添加方差线
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()

首先，XGB中的树的数量决定了模型的学习能力，树的数量越多，模型的学习能力越强。只要XGB中树的数量足够了，即便只有很少的数据， 模型也能够学到训练数据100%的信息，所以XGB也是天生过拟合的模型。但在这种情况下，模型会变得非常不稳定。

第二，XGB中树的数量很少的时候，对模型的影响较大，当树的数量已经很多的时候，对模型的影响比较小，只能有
微弱的变化。当数据本身就处于过拟合的时候，再使用过多的树能达到的效果甚微，反而浪费计算资源。当唯一指标或者准确率给出的n_estimators看起来不太可靠的时候，我们可以改造学习曲线来帮助我们。

第三，树的数量提升对模型的影响有极限，最开始，模型的表现会随着XGB的树的数量一起提升，但到达某个点之后，树的数量越多，模型的效果会逐步下降，这也说明了暴力增加n_estimators不一定有效果。

这些都和随机森林中的参数n_estimators表现出一致的状态。在随机森林中我们总是先调整n_estimators，当n_estimators的极限已达到，我们才考虑其他参数，但XGB中的状况明显更加复杂，当数据集不太寻常的时候会更加复杂。这是我们要给出的第一个超参数，因此还是建议优先调整n_estimators，一般都不会建议一个太大的数目，300以下为佳

1.2 有放回随机抽样：重要参数subsample

在无论是装袋还是提升的集成算法中，有放回抽样都是我们防止过拟合，让单一弱分类器变得更轻量的必要操作。实际应用中，每次抽取50%左右的数据就能够有不错的效果了。sklearn的随机森林类中也有名为boostrap的参数来帮助我们控制这种随机有放回抽样。

同时，这样做还可以保证集成算法中的每个弱分类器（每棵树）都是不同的模型，基于不同的数据建立的自然是不同的模型，而集成一系列一模一样的弱分类器是没有意义的。在梯度提升树中，我们每一次迭代都要建立一棵新的树，因此我们每次迭代中，都要有放回抽取一个新的训练样本。

不过，这并不能保证每次建新树后，集成的效果都比之前要好。因此我们规定，在梯度提升树中，每构建一个评估
器，都让模型更加集中于数据集中容易被判错的那些样本。

采样除了让模型更加集中于那些困难样本，还对模型造成了什么样的影响呢？
采样会减少样本数量，而从学习曲线来看样本数量越少模型的过拟合会越严重，因为对模型来说，数据量越少模型学习越容易，学到的规则也会越具体越不适用于测试样本。所以subsample参数通常是在样本量本身很大的时候来调整和使用。

axisx = np.linspace(0,1,20)
rs = []
for i in axisx:
    reg = XGBR(n_estimators=180,subsample=i,random_state=420)
    rs.append(CVS(reg,Xtrain,Ytrain,cv=cv).mean())
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="green",label="XGB")
plt.legend()
plt.show()

#继续细化学习曲线
axisx = np.linspace(0.05,1,20)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=180,subsample=i,random_state=420)
    cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()

#细化学习曲线
axisx = np.linspace(0.75,1,25)
rs = []
var = []
ge = []
for i in axisx:
    reg = XGBR(n_estimators=180,subsample=i,random_state=420)
    cvresult = CVS(reg,Xtrain,Ytrain,cv=cv)
    rs.append(cvresult.mean())
    var.append(cvresult.var())
    ge.append((1 - cvresult.mean())**2+cvresult.var())
print(axisx[rs.index(max(rs))],max(rs),var[rs.index(max(rs))])
print(axisx[var.index(min(var))],rs[var.index(min(var))],min(var))
print(axisx[ge.index(min(ge))],rs[ge.index(min(ge))],var[ge.index(min(ge))],min(ge))
rs = np.array(rs)
var = np.array(var)
plt.figure(figsize=(20,5))
plt.plot(axisx,rs,c="black",label="XGB")
plt.plot(axisx,rs+var,c="red",linestyle='-.')
plt.plot(axisx,rs-var,c="red",linestyle='-.')
plt.legend()
plt.show()

1.3 迭代决策树：重要参数eta

如何保证必须每次新添加的树一定得是对这个新数据集预测效果最优的那一棵树。
类比逻辑回归：

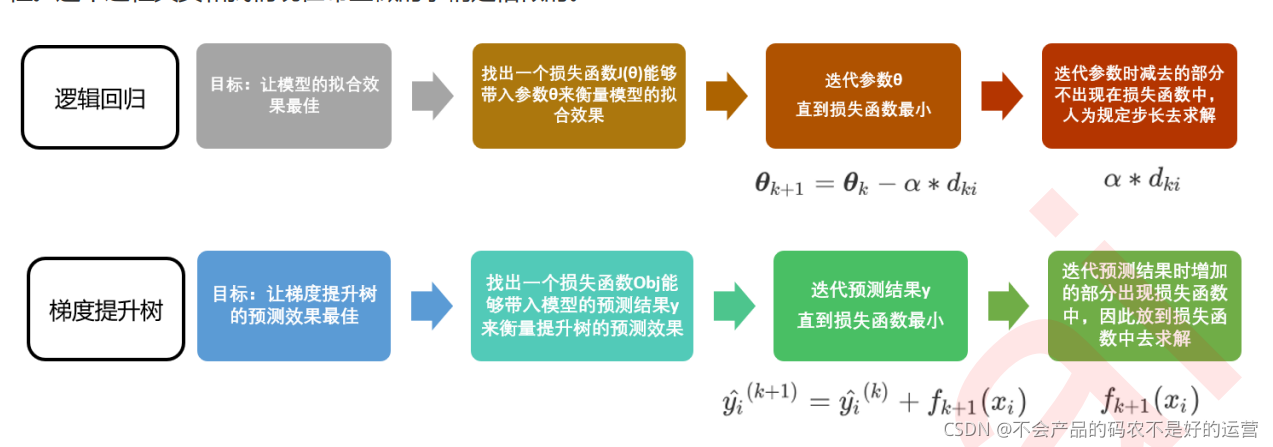
完整的迭代决策树公式：

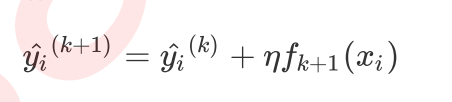
其中η读作"eta"，是迭代决策树时的步长（shrinkage），又叫做学习率（learning rate），η越大，迭代的速度越快，算法的极限很快被达到，有可能无法收敛到真正的最佳。η 越小，越有可能找到更精确的最佳值，更多的空间被留给了后面建立的树，但迭代速度会比较缓慢。

#首先我们先来定义一个评分函数，这个评分函数能够帮助我们直接打印Xtrain上的交叉验证结果
def regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2"],show=True):
    score = []
    for i in range(len(scoring)):
        if show:
            print("{}:{:.2f}".format(scoring[i] #模型评估指标的名字
                                     ,CVS(reg
                                          ,Xtrain,Ytrain
                                          ,cv=cv,scoring=scoring[i]).mean()))
        score.append(CVS(reg,Xtrain,Ytrain,cv=cv,scoring=scoring[i]).mean())
    return score
#观察一下eta如何影响我们的模型：
from time import time
import datetime
for i in [0,0.2,0.5,1]:
    time0=time()
    reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
    print("learning_rate = {}".format(i))
    regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"])
    print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
    print("\t")
axisx = np.arange(0.05,1,0.05)
rs = []
te = []
for i in axisx:
    reg = XGBR(n_estimators=180,random_state=420,learning_rate=i)
    score = regassess(reg,Xtrain,Ytrain,cv,scoring = ["r2","neg_mean_squared_error"],show=False)
    test = reg.fit(Xtrain,Ytrain).score(Xtest,Ytest)
    rs.append(score[0])
    te.append(test)
print(axisx[rs.index(max(rs))],max(rs))
plt.figure(figsize=(20,5))
plt.plot(axisx,te,c="gray",label="test")
plt.plot(axisx,rs,c="green",label="train")
plt.legend()
plt.show()

虽然从图上来说，默认的0.1看起来是一个比较理想的情况，并且看起来更小的步长更利于现在的数据，但我们也无法确定对于其他数据会有怎么样的效果。所以通常，我们不调整 ，即便调整，一般它也会在[0.01,0.2]之间变动。如果我们希望模型的效果更好，更多的可能是从树本身的角度来说，对树进行剪枝，而不会寄希望于调整η

2 XGBoost

class xgboost.XGBRegressor (kwargs，max_depth=3, learning_rate=0.1, n_estimators=100, silent=True,
objective='reg:linear', booster='gbtree', n_jobs=1, nthread=None, gamma=0, min_child_weight=1,
max_delta_step=0, subsample=1, colsample_bytree=1, colsample_bylevel=1, reg_alpha=0, reg_lambda=1,
scale_pos_weight=1, base_score=0.5, random_state=0, seed=None, missing=None, importance_type='gain')

2.1 选择弱评估器：重要参数booster

梯度提升算法中不只有梯度提升树，XGB作为梯度提升算法的进化，自然也不只有树模型一种弱评估器。在XGB中，除了树模型，我们还可以选用线性模型，比如线性回归，来进行集成。虽然主流的XGB依然是树模型，但我们也可以使用其他的模型。基于XGB的这种性质，我们有参数“booster"来控制我们究竟使用怎样的弱评估器。

for booster in ["gbtree","gblinear","dart"]:
    reg = XGBR(n_estimators=180
               ,learning_rate=0.1
               ,random_state=420
               ,booster=booster).fit(Xtrain,Ytrain)
    print(booster)
    print(reg.score(Xtest,Ytest))

2.2 XGB的目标函数：重要参数objective

梯度提升算法中都存在着损失函数。不同于逻辑回归和SVM等算法中固定的损失函数写法，集成算法中的损失函数是可选的，要选用什么损失函数取决于我们希望解决什么问题，以及希望使用怎样的模型。比如说，如果我们的目标是进行回归预测，那我们可以选择调节后的均方误差RMSE作为我们的损失函数。如果我们是进行分类预测，那我们可以选择错误率error或者对数损失log_loss。只要我们选出的函数是一个可微的，能够代表某种损失的函数，它就可以是我们XGB中的损失函数.


看xgb自身的调用方式：

#xgb实现法
#使用类Dmatrix读取数据
dtrain = xgb.DMatrix(xtrain,ytrain)
dtest = xgb.DMatrix(xtest,ytest)
param = {'silent':False,#silent默认为False，通常需要手动将它关闭
        'objective':'reg:linear',
        'eta':0.1}
num_round = 180
#类train，可以直接导入的参数是训练数据，树的数量，其他参数都需要通过params来导入
bst = xgb.train(param, dtrain, num_round)
r2_score(ytest,bst.predict(dtest))
MSE(ytest,bst.predict(dtest))

2.3 参数化决策树fk(x)：参数alpha，lambda

当λ和α越大，惩罚越重，正则项所占的比例就越大，在尽全力最小化目标函数的最优化方向下，叶子节点数量就会被压制，模型的复杂度就越来越低，所以对于天生过拟合的XGB来说，正则化可以一定程度上提升模型效果。

#使用网格搜索来查找最佳的参数组合
from sklearn.model_selection import GridSearchCV
param = {"reg_alpha":np.arange(0,5,0.05),"reg_lambda":np.arange(0,2,0.05)}
gscv = GridSearchCV(reg,param_grid = param,scoring = "neg_mean_squared_error",cv=cv)

param = {'reg_alpha':np.arange(0,5,0.05),'reg_lambda':np.arange(0,2,0.05)}
gscv = GridSearchCV(reg,param_grid=param,scoring = 'neg_mean_squared_error',cv=cv)
time0 = time()
gscv.fit(xtrain,ytrain)
print(datetime.datetime.fromtimestamp(time()-time0).strftime('%M:%s:%f'))

2.4 让树停止生长：重要参数gamma

import xgboost as xgb

#为了便捷，使用全数据
dfull = xgb.DMatrix(X,y)
#设定参数
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
num_round = 100
n_fold=5 #sklearn - KFold
#使用类xgb.cv
time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
#看看类xgb.cv生成了什么结果？
cvresult1 #随着树不断增加，我们的模型的效果如何变化
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,101),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,101),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()

#从这个图中，我们可以看出什么？
#怎样从图中观察模型的泛化能力？
#从这个图的角度来说，模型的调参目标是什么？
param1 = {'silent':True,'obj':'reg:linear',"gamma":0,"eval_metric":"mae"}
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)

plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.legend()
plt.show()
param1 = {'silent':True,'obj':'reg:linear',"gamma":0}
param2 = {'silent':True,'obj':'reg:linear',"gamma":20}
num_round = 180
n_fold=5

time0 = time()
cvresult1 = xgb.cv(param1, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
time0 = time()
cvresult2 = xgb.cv(param2, dfull, num_round,n_fold)
print(datetime.datetime.fromtimestamp(time()-time0).strftime("%M:%S:%f"))
plt.figure(figsize=(20,5))
plt.grid()
plt.plot(range(1,181),cvresult1.iloc[:,0],c="red",label="train,gamma=0")
plt.plot(range(1,181),cvresult1.iloc[:,2],c="orange",label="test,gamma=0")
plt.plot(range(1,181),cvresult2.iloc[:,0],c="green",label="train,gamma=20")
plt.plot(range(1,181),cvresult2.iloc[:,2],c="blue",label="test,gamma=20")
plt.legend()
plt.show()

#从这里，你看出gamma是如何控制过拟合了吗？控制训练集上的训练 - 降低训练集上的表现

3 XGBoost应用中的其他问题

3.1 过拟合：剪枝参数与回归模型调参

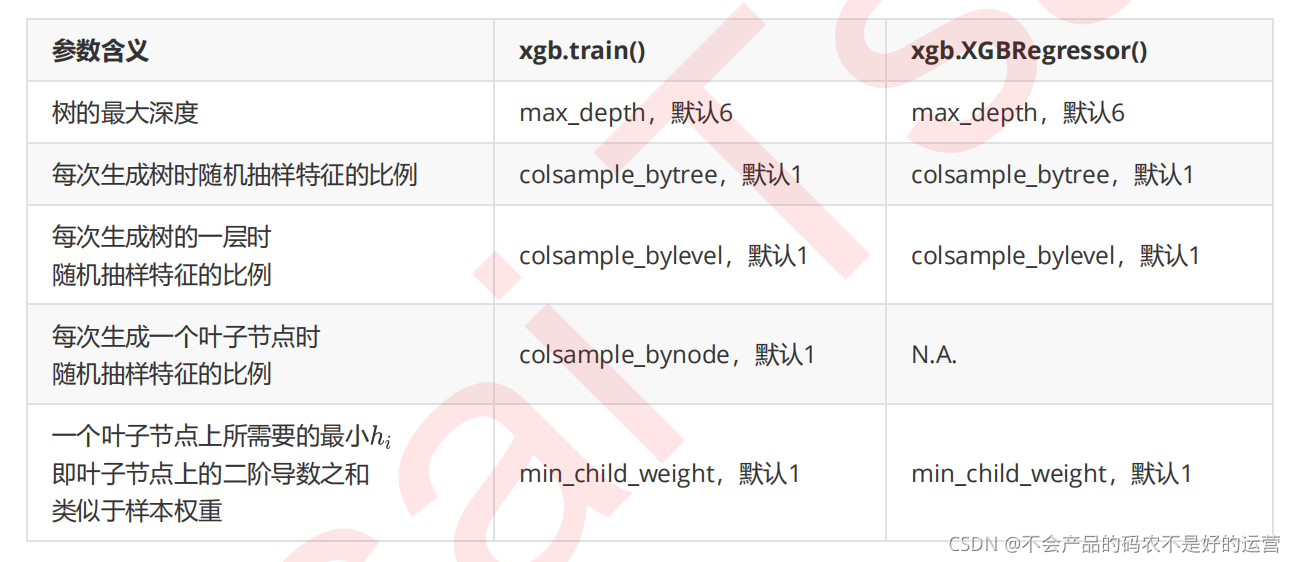
这些参数中，树的最大深度是决策树中的剪枝法宝，算是最常用的剪枝参数，不过在XGBoost中，最大深度的功能与参数 相似，因此如果先调节了 ，则最大深度可能无法展示出巨大的效果。当然，如果先调整了最大深度，则 也有可能无法显示明显的效果。通常来说，这两个参数中我们只使用一个，不过两个都试试也没有坏处。

三个随机抽样特征的参数中，前两个比较常用。在建立树时对特征进行抽样其实是决策树和随机森林中比较常见的一种方法，但是在XGBoost之前，这种方法并没有被使用到boosting算法当中过。Boosting算法一直以抽取样本（横向抽样）来调整模型过拟合的程度，而实践证明其实纵向抽样（抽取特征）更能够防止过拟合。

参数min_child_weight不太常用，它是一篇叶子上的二阶导数 之和，当样本所对应的二阶导数很小时，比如说为
0.01，min_child_weight若设定为1，则说明一片叶子上至少需要100个样本。本质上来说，这个参数其实是在控制
叶子上所需的最小样本量，因此对于样本量很大的数据会比较有效。如果样本量很小（比如我们现在使用的波士顿房价数据集，则这个参数效用不大）。就剪枝的效果来说，这个参数的功能也被 替代了一部分，通常来说我们会试试看这个参数，但这个参数不是我的优先选择。

通常当我们获得了一个数据集后，我们先使用网格搜索找出比较合适的n_estimators和eta组合，然后使用gamma或 者max_depth观察模型处于什么样的状态（过拟合还是欠拟合，处于方差-偏差图像的左边还是右边？），最后再决定是否要进行剪枝。通常来说，对于XGB模型，大多数时候都是需要剪枝的。接下来我们就来看看使用xgb.cv这个类来进行剪枝调参，以调整出一组泛化能力很强的参数。