1. 采用 PCA 对男女生样本数据中的(身高、体重、鞋码、50m 成绩、肺活量) 共 5 个特征进行特征降维,并实现 LDA 算法对处理后的特征进行分类,计算 模型预测性能(包含 SE、SP、ACC 和 AUC),试分析 LDA 算法如果作为降维 技术对于各性能指标的影响。
2. 实现基于信息增益率进行划分选择的决策树算法,对男女生样本数据中的(喜 欢颜色,喜欢运动,喜欢文学)3 个特征进行分类,计算模型预测性能(包 含 SE、SP、ACC),并以友好的方式图示化结果。
本文的运行环境是windows+Pycharm+python3.8。
数据部分如下
其中,男1女0,喜欢1不喜欢0,总样本数据数351,其中男生样本数量为283,女生样本数量为68;训练集样本数量为245,测试集样本数量为106;其中测试集约占样本总数的30%。

目录
1.1 PCA降维
用PCA对男女生样本数据中的身高、体重、鞋码、50m 成绩、肺活量5维特征进行降维处理,得到可视化结果,本次实验选择降到2维。

图1?PCA降维后的二维数据?
这里选择投影后方差最大的身高、体重两个特征,其投影后特征维度的方差分别为7.59619030e+05和1.21208785e+02。


图2为原始的男女身高体重样本信息和经过PCA降维处理后的特征信息的对比。
1.2 LDA降维处理
????? 用LDA对男女生样本数据中的身高、体重、鞋码、50m 成绩、肺活量5维特征进行降维处理,得到可视化结果,本次实验选择降到二维和一维。
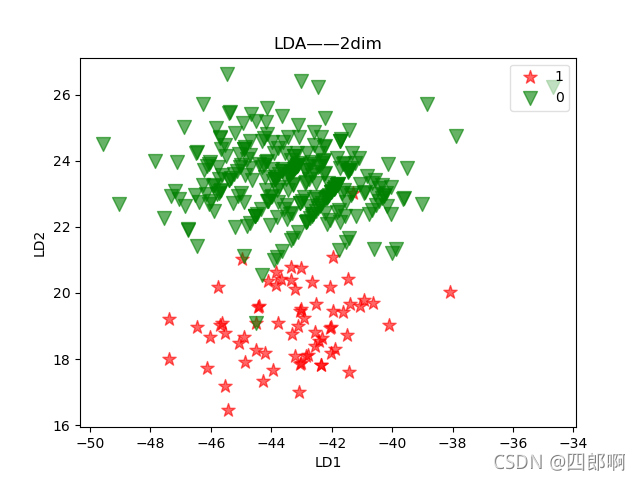
图3 LDA 降维后的二维数据可视化

图4 LDA 降维后的一维数据可视化
?为方便观察降各点的纵坐标,本文将其设为两类样本的标签值0(女),1(男),通过图1.2.1可以发现,经过LDA降维处理后的两类数据分别投影到两条直线上,数据类间样本距离较远,而类内样本距离较近。
选取100个样本进行模型效果测试,特征维数为5维,聚类中心为2

?图5 LDA分类器的分类效果展示
从上方对比图中,我们可以发现LDA降维至一维和二维特征,数据的分类效果都不错,接下来本文选择使用LDA降至一维的特征数据继续实验。
1.3 基于PCA和LDA降维的SVM分类的模型指标
本次实验使用机器学习库scikit-learn建立SVM模型,分别沿用经过PCA和LDA降至一维的数据集。其中,经过PCA、LDA降维处理的数据集为:原始数据条数:351;训练数据条数:210;特征个数:2;
将经过PCA、LDA降维处理的数据,送入到SVM中进行训练得出训练模型,然后将测试集标签和通过训练模型得出的score两组数据经过roc_curve函数,最终返回真正率和假正率以及阈值。
最终得到的AUC为0.9836182336182336;SP、SE以及Threshold见表1。
| SP | 1. | 1. | 1. | 0.9583 | 0.9583 | 0. |
| SE | 0. | 0.0085 | 0.6068 | 0.6068 | 1. | 1. |
| Threshold | 12.8081 | 11.8081 | 4.4613 | 4.4445 | 0.4696 | -9.0282 |
表1 LDA模型指标
经过PCA降维数据的分类模型参数的AUC: 0.8294159544159544;由于Threshold(阈值)数多大28个这里就不再展示。
 ?
?
?图6 LDA_1dim_ROC曲线,图7 PCA_1dim_ROC曲线
通过对比图6和图7很容易的得出:图6LDA特征集合的ROC曲线更靠近左上角,其试验的FPR高于图7和FPR低于图7,即灵敏度更高,误判率更低。两幅图ROC曲线的area分别为0.98和0.83。LDA图的最佳分类点处的TPR值为1,同时FPR接近0,而PCA图的最佳分类点处的TPR值为不足0.8,同时FPR接近0.2。因此针对本实验数据集在进行数据降维时,选择LDA的分类性能效果要远优于选择PCA。
2. 实现基于信息增益率进行划分选择的决策树算法,对男女生样本数据中的(喜 欢颜色,喜欢运动,喜欢文学)3 个特征进行分类,计算模型预测性能(包 含 SE、SP、ACC),并以友好的方式图示化结果。
2.1 决策树
2.1.1 样本数据集
本次决策树的构建使用总为样本数据351,其中男生样本数量为283,女生样本数量为68;训练集样本数量为245,测试集样本数量为106;其中测试集约占样本总数的30%。
2.1.2 决策树可视化

2.2 模型分类性能预测
2.2.1 模型稳定性
性能度量是衡量模型泛化能力的评价标准,反映了任务需求;使用不同的性能度量往往会导致不同的评判结果。
????? 首先,利用score(),输入测试样本的数据和标签,返回经过测试样本预测后模型的分类score;
第二步:得到分数后,再做十次交叉验证,看模型的稳定性。利用sklearn 中的cross_val_score函数进行交叉验证,输入数据特征与数据标签,这里cv设置为10,进行十次交叉验证,返回测试分数也是0.8019,由此可知模型稳定性良好;
| list | Score |
| 测试集 | 0.8019 |
| 十次交叉验证 | 0.8019 |
| 调整树深 | 0.8063 |
第三步:调整参数,这里主要针对决策树的深度,为了看看到底是过拟合还是欠拟合,这里我们把训练集和测试集的表现都比较一下。由表2.2.1得知结果为0.8063,从图2.2.1 可以看到是有过拟合的倾向。

2.2.2 SE、SP、ACC分类性能预测
本次预测任务,使用决策树中的函数predict(),对测试集的106个样本进行预测,返回样本的预测标签。根据测试集的真实标记与预测结果计算样本的评价指标TP、TN、FP、FN,然后在算出SE、SP、ACC等评价指标。
列表如下,其中1代表正类,0代表负类:

其中,TP 表示预测正确的正样本;TN 表示预测正确的负样本;FP 表示预测错误的负样本 ;FN表示预测错误的正样本。
敏感性(SE)=TP/(TP+FN) #tpr
特异性(SP)=TN/(TN+FP) # tnr=1-fpr
准确率(ACC)=(TP+TN)/(TP+FP+TN+FN)
模型预测性能如表4
| 敏感性SE | 特异性SP | 准确率ACC |
| 0.942 | 0.300 | 0.821 |
?表 4 决策树分类性能评估
从表中可知,由ACC准确率可知,能够被正确预测的样本高达总数的82.1%;由敏感性SE可知,该模型对男生(正样本)的预测正确率高达94.2%;而由特异性SP可知,该模型对女生(负样本)的分类正确率只有30%,这可能是在模型训练的过程中,女生(负样本)数量过少,导致训练的模型不够准确,因而正确率不高。
# 代码段
?1.PCA由5维特征降到2维代码
图1PCA降维后的二维数据?
# 建立工程,导入sklearn 相关工具包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
'''
/**************************task1**************************/
1.1. 采用 PCA 对男女生样本数据中的(身高、体重、鞋码、50m 成绩、肺活量)
共 5 个特征进行特征降维,并实现 LDA 算法对处理后的特征进行分类,计算
模型预测性能(包含 SE、SP、ACC 和 AUC),试分析 LDA 算法如果作为降维
技术对于各性能指标的影响。
/**************************task1**************************/
'''
# 加载数据
data = pd.io.parsers.read_csv('data.txt', header=0, sep=' ')
data.dropna(how='any', inplace=True)
feature_names = ['身高(cm)', '体重(kg)', '鞋码', '50米成绩', '肺活量']
X = data[feature_names].values # 男女五个特征数据的集合
y = data['sex'].values
print(type(X))
print(type(y))
print(y)
print(y[0])
# PCA进行降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
print(X_pca)
# 3 按类别对降维后的数据进行保存
man_x, man_y = [], []
woman_x, woman_y = [], []
m, n = np.shape(X)
for i in range(m):
if y[i] == 1:
man_x.append(X_pca[i][0])
man_y.append(X_pca[i][1])
elif y[i] == 0:
woman_x.append(X_pca[i][0])
woman_y.append(X_pca[i][1])
# 4 降维后数据可视化
plt.figure(1)
plt.title('PCA_2dim')
p1 = plt.scatter(man_x, man_y, c='g', marker='*', alpha=0.6)
p2 = plt.scatter(woman_x, woman_y, c='r', marker='*', alpha=0.6)
gender_label = ['boy', 'girl']
plt.legend([p1, p2], gender_label, loc=0)
plt.xlabel('x')
plt.ylabel('y')
plt.savefig("PCA_2dim.png")
plt.show()2.LDA模型性能测试
图3 LDA 降维后的二维数据可视化
图4 LDA 降维后的一维数据可视化
图5 LDA分类器的分类效果展示
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
'''
/**************************task1**************************/
1.2. 采用 PCA 对男女生样本数据中的(身高、体重、鞋码、50m 成绩、肺活量)
共 5 个特征进行特征降维,并实现 LDA 算法对处理后的特征进行分类,计算
模型预测性能(包含 SE、SP、ACC 和 AUC),试分析 LDA 算法如果作为降维
技术对于各性能指标的影响。
1.PCA LDA 降维后的对比 优缺点 细节 具体向量
2.LDA 用于分类
/**************************task1**************************/
'''
# 第一步数据载入
data = pd.io.parsers.read_csv('data.txt', header=0, sep=' ')
data.dropna(how='any', inplace=True)
# 第二步提取数据的X轴和y轴信息
feature_names = ['身高(cm)', '体重(kg)', '鞋码', '50米成绩', '肺活量']
X = data[feature_names].values # 男女三个特征数据的集合
y = data['sex'].values
# print(X)
# 第三步 使用Label_encoding进行标签的数字转换
from sklearn.preprocessing import LabelEncoder
model = LabelEncoder().fit(y)
y = model.transform(y) + 1 # +1 所以从1开始
labels_type = np.unique(y) # print(labels_type):[1,2] 1--女,2--男
# 第四步 计算类内距离Sw
Sw = np.zeros([5, 5]) # Sw = np.zeros((X.shape[1], X.shape[1]))
# 循环每一种类型
print(labels_type)
for i in range(1, 5):
xi = X[y == i] # x1--女 x2--男
ui = np.mean(xi, axis=0) # 每个类别的均值1*3array
sw = ((xi - ui).T).dot(xi-ui)
Sw += sw
print('类内距离Sw:', Sw)
# 第五步:计算类间距离SB
SB = np.zeros([5, 5])
u = np.mean(X, axis=0).reshape(5, 1) # 所有类别的均值向量--3*1array
print(u, 'means')
for i in range(1, 3): # 分为男女生两类 1-2
ni = X[y == i].shape[0] # 每个类别含多少人 shape(0)--矩阵行数;shape(1)--矩阵列数
print(ni, '男女生人数')
ui = np.mean(X[y == i], axis=0).reshape(5, 1) # 某个类别的平均值
print(ui, '男女生在每一类的均值')
sb = ni * (ui - u).dot((ui - u).T) # 5*5矩阵
print(sb, '$$')
SB += sb
print('类间距离SB:', SB)
# 第六步:使用Sw^-1*SB特征向量计算w
vals, eigs = np.linalg.eig(np.linalg.inv(Sw).dot(SB)) # 返回Sw^-1*SB(3*3)的特征值和特征向量
print('Sw^-1*SB的特征值:', vals)
print('Sw^-1*SB的特征向量:', eigs)
# 第七步:取前两个特征向量作为w(投影矩阵),与X进行相乘操作,相当于进行了2维度的降维操作
w = np.vstack([eigs[:, 0], eigs[:, 1]]).T # 5*2
print('投影矩阵:', w) # 5*2
transform_X = X.dot(w) # 总数*5 * 5*2 = 总数*2维矩阵 transform_X:经过降维后的数据
# print('经过降维后的数据:', transform_X)
# 第八步:定义画图函数
labels_dict = data['sex'].unique()
print(labels_dict) # [1,0]
def plot_lda():
ax = plt.subplot(111) # # 使用plt.subplot来创建小图. plt.subplot(111)表示将整个图像窗口分为1行1列, 当前位置为1.
for label, m, c in zip(labels_type, ['*', 'v'], ['red', 'green']):
p = plt.scatter(transform_X[y == label][:, 0], transform_X[y == label][:, 1], c=c, marker=m, alpha=0.6, s=100, label=labels_dict[label-1])
plt.xlabel('LD1')
plt.ylabel('LD2')
# 定义图例,loc表示的是图例的位置
leg = plt.legend(loc='upper right', fancybox=True)
# 设置图例的透明度为0.6
leg.get_frame().set_alpha(0.6)
plt.title('LDA——2dim')
plt.savefig("LDA.png")
plt.show()
plot_lda()
# LDA模型测试
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# from sklearn.datasets.samples_generator import make_classification
from mpl_toolkits.mplot3d import Axes3D
def LDA(X, y):
X1 = np.array([X[i] for i in range(len(X)) if y[i] == 0])
X2 = np.array([X[i] for i in range(len(X)) if y[i] == 1])
len1 = len(X1)
len2 = len(X2)
mju1 = np.mean(X1, axis=0) # 求中心点
mju2 = np.mean(X2, axis=0)
cov1 = np.dot((X1 - mju1).T, (X1 - mju1))
cov2 = np.dot((X2 - mju2).T, (X2 - mju2))
Sw = cov1 + cov2
w = np.dot(np.mat(Sw).I, (mju1 - mju2).reshape((len(mju1), 1))) # 计算w
X1_new = func(X1, w) # 训练集特征
X2_new = func(X2, w) # 测试集特征
y1_new = [1 for i in range(len1)] # 训练集标签
y2_new = [2 for i in range(len2)] # 测试集标签
return X1_new, X2_new, y1_new, y2_new
def func(x, w):
return np.dot((x), w)
if '__main__' == __name__:
X, y = make_blobs(n_samples=100, n_features=5, centers=2,
cluster_std=1.5, random_state=10)
X1_new, X2_new, y1_new, y2_new = LDA(X, y) # 训练集特征 # 测试集特征 # 训练集标签 # 测试集标签
plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)
plt.title('LDA_2dim')
plt.savefig("LDA_2dim.png")
plt.show()
plt.plot(X1_new, y1_new, 'b*')
plt.plot(X2_new, y2_new, 'ro')
plt.title('LDA_1dim')
plt.savefig("LDA_1dim.png")
plt.show()
3.模型性能指标 SE SP AUC?
图6 LDA_1dim_ROC曲线
图7 PCA_1dim_ROC曲线
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
import warnings
import sklearn
from sklearn.linear_model import LogisticRegressionCV
from sklearn.exceptions import ConvergenceWarning
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import label_binarize
from sklearn import metrics
from sklearn.decomposition import PCA
# 设置字符集,防止中文乱码
mpl.rcParams['font.sans-serif']=[u'simHei']
mpl.rcParams['axes.unicode_minus']=False
# 拦截异常
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
# 数据加载
'''
path = "data.txt"
names = ['身高(cm)', '体重(kg)', '鞋码', '50米成绩', '肺活量', 'sex']
df = pd.read_csv(path, header=None, names=names)
df['sex'].value_counts()
print(df.head())
'''
# 第一步数据载入
data = pd.io.parsers.read_csv('data.txt', header=0, sep=' ')
data.dropna(how='any', inplace=True)
names = ['身高(cm)', '体重(kg)', '鞋码', '50米成绩', '肺活量', 'sex']
def parseRecord(record):
result=[]
r = zip(names,record)
for name,v in r:
if name == 'sex':
if v == '1':
result.append(1)
elif v == '0':
result.append(2)
else:
result.append(np.nan)
else:
result.append(float(v))
return result
# 1. 数据转换为数字以及分割
# 数据分割_提取数据的X轴和y轴信息
feature_names = ['身高(cm)', '体重(kg)', '鞋码', '50米成绩', '肺活量']
X = data[feature_names].values # 男女三个特征数据的集合
y = data['sex'].values
# 3. 特征选择
# 4. 降维处理
# LDA_1dim
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X,y)
X_new = lda.transform(X)
plt.scatter(X_new[:, -1], y,marker='o',c=y)
plt.title('LDA_1dim')
plt.savefig("LDA_1dim.png")
plt.show()
# pca_1dim
pca = PCA(n_components=1)
X_pca = pca.fit_transform(X)
# 数据抽样(训练数据和测试数据分割)
X_train,X_test,Y_train,Y_test = train_test_split(X_pca, y, test_size=0.4, random_state=0)
print ("原始数据条数:%d;训练数据条数:%d;特征个数:%d;测试样本条数:%d" % (len(X), len(X_train), X_train.shape[1], X_test.shape[0]))
# 2. 数据标准化
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
# print(X_train)
# print(X_test)
# Learn to predict each class against the other
from sklearn import svm
svm = svm.SVC(kernel='linear', probability=True, random_state=None)
# 通过decision_function()计算得到的y_score的值,用在roc_curve()函数中
y_score = svm.fit(X_train, Y_train).decision_function(X_test)
print(Y_test)
print(y_score)
# Compute ROC curve and ROC area for each class
# [pred, acc, preb] = svmpredict(Y_test, X_test, y_score, '-b 1');
fpr, tpr, threshold = metrics.roc_curve(Y_test, y_score) # 计算真正率和假正率
print('SP:', 1-fpr, 'SE:', tpr, 'threshold:', threshold)
roc_auc = metrics.auc(fpr, tpr) # 计算auc的值
print('AUC:', roc_auc)
plt.figure()
lw = 2
plt.figure(figsize=(10, 10))
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc) ###假正率为横坐标,真正率为纵坐标做曲线
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()# 决策树及其模型指标SE、SP、ACC
图8 决策树
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
import math
'''
/**************************task1**************************/
2. 实现基于信息增益率进行划分选择的决策树算法,对男女生样本数据中的(喜
欢颜色,喜欢运动,喜欢文学)3 个特征进行分类,计算模型预测性能(包
含 SE敏感性=TP/(TP+FN)、SP特异性=TN/(TN+FP)、ACC=right/all=(TP+TN)/(TP+FP+TN+FN),并以友好的方式图示化结果
1.构建树步骤(数据处理。。知乎) 分类图
2.预测性能
/**************************task1**************************/
'''
import pandas as pd
import numpy as np
data = pd.read_csv('data_favorite.txt', header=0, sep=' ')
# data.dropna(how='any', inplace=True) # type(data)--pandas.core.frame.DataFrame
# 处理非数字
data["color"] = pd.factorize(data["color"])[0].astype(np.uint16)
# print(data)
# 拆分数据
# 先把数据和标签拆分,
X = data.iloc[:, data.columns != "sex"]
y = data.iloc[:, data.columns == "sex"]
# 首先将pandas读取的数据转化为array
X = np.array(X)
y = np.array(y)
# 然后按经典的三七分,把数据拆分。由于是随机抽取的,所以索引是乱的。
from sklearn.model_selection import train_test_split
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.3)
# print('Xtrain:',Xtrain)
# print('Xtest:', Xtest)
# print('Ytrain:',Ytrain)
# print('Ytest:', Ytest)
print(len(Xtrain))
print(len(Xtest))
# 修正测试集和训练集的索引
'''
for i in [Xtrain, Xtest, Ytrain, Ytest]:
i.index = range(i.shape[0])
'''
# 训练模型。得到分数后,再做十次交叉验证,看看模型的稳定性
clf = DecisionTreeClassifier(random_state=25)
clf = clf.fit(Xtrain, Ytrain)
#根据真实值和预测值计算评价指标
def performance(labelArr, predictArr): # 样本一定要是数组narray类型 类标签为1,0 # labelArr[i]真实的类别,predictArr[i]预测的类别
# labelArr[i] is actual value,predictArr[i] is predict value
TP = 0.; TN = 0.; FP = 0.; FN = 0.
for i in range(len(labelArr)):
if labelArr[i] == 1 and predictArr[i] == 1:
TP += 1.
elif labelArr[i] == 1 and predictArr[i] == 0:
FN += 1.
elif labelArr[i] == 0 and predictArr[i] == 1:
FP += 1.
elif labelArr[i] == 0 and predictArr[i] == 0:
TN += 1.
SE = TP / (TP + FN) # Sensitivity = TP/P and P = TP + FN
SP = TN / (FP + TN) # Specificity = TN/N and N = TN + FP
# MCC = (TP * TN - FP * FN) / math.sqrt((TP + FP) * (TP + FN) * (TN + FP) * (TN + FN))
ACC = (TP + TN) / (TP + TN + FP + FN)
return SE, SP, ACC
predict_label = clf.predict(Xtest)
print(predict_label)
# print(type(predict_label))
print('Ytest:', Ytest)
# print(type(Ytest))
print(performance(Ytest, predict_label)) # 测试集特征经过决策树判断出的标签与测试集实际标签输入performance
score_ = clf.score(Xtest, Ytest)
print('训练测试的分数:', score_) # 进行十次交叉验证
# 进行十次交叉验证
score = cross_val_score(clf, X, y, cv=10).mean()
print('进行十次交叉验证:', score_)
# 调整参数
# 先从max_depth开始调,为了看看到底是过拟合还是欠拟合,最好还是把训练集和测试集的表现都比较一下。
tr = []
te = []
for i in range(10):
clf = DecisionTreeClassifier(random_state=25, max_depth=i+1,
criterion="entropy")
clf = clf.fit(Xtrain, Ytrain)
score_tr = clf.score(Xtrain,Ytrain)
score_te = cross_val_score(clf,X,y,cv=10).mean()
tr.append(score_tr)
te.append(score_te)
print(max(te))
plt.plot(range(1,11),tr,color="red",label="train")
plt.plot(range(1,11),te,color="blue",label="test")
plt.xticks(range(1,11))
plt.legend()
plt.title('Train-Test Accuracy')
plt.savefig(" Decision Tree Train-test Accuracy")
plt.show()
'''
'''
from sklearn import tree
tree.plot_tree(clf)
plt.show()
# 可视化决策树
import graphviz
clf = DecisionTreeClassifier(random_state=25, max_depth=i+1, criterion="entropy")
clf = clf.fit(Xtrain, Ytrain)
tree.export_graphviz(clf, out_file='tree.dot')
data_feature_names = ['color', 'sports', 'literature']
# Visualize data
dot_data = tree.export_graphviz(clf,
out_file=None,
feature_names=data_feature_names,
class_names=['girl', 'boy'],
filled=True,
rounded=True,
special_characters=True)
import pydotplus
graph = pydotplus.graph_from_dot_data(dot_data)
colors = ('turquoise', 'orange')
import collections
edges = collections.defaultdict(list)
for edge in graph.get_edge_list():
edges[edge.get_source()].append(int(edge.get_destination()))
for edge in edges:
edges[edge].sort()
for i in range(2):
dest = graph.get_node(str(edges[edge][i]))[0]
dest.set_fillcolor(colors[i])
graph.write_png('tree.png')