? ? ? ? 决策树这一章节已经写过类似的了:具体的特征选择算法可以看以前的文章:
? ? ? ? 里面都详细地介绍了ID3,C4.5,还有GINI系数三种特征选择方法了
????????
? ? ? ? 除此之外,书上还提高了他们之间的对比,这里可以着重看一下:
1. ID3 和C4.5 的提升点在哪里
? ? ? ? 这里其实上面提到的文章也说了,但是这里再说一次:
? ? ? ? ID3会优先选择那些特征的取值较多的特征,根据此特征划分更容易得到纯度更高的子集,因此划分之后的熵更低,由于划分前的熵是一定的,因此信息增益更大,因此信息增益比较 偏向取值较多的特征。自己的话理解就是,因为我这个特征的取值可以非常多,所以可以非常好地过拟合地适应训练集的数据,所以我们可以更容易得到纯度更高的子集,从而使得信息增益比更加高。
? ? ? ? ID3的规则下,信息增益越大,代表这个特征越管用,我们应该选
? ? ? ? 所以 C4.5就会在 在ID3的基础上(信息增益的基础上)乘上一个惩罚参数。特征个数较多时,惩罚参数较小;特征个数较少时,惩罚参数较大。用来遏制ID3因为取值多而结果大的情况
? ? ? ? 再换句话说就是现在候选特征中找出 信息增益 高于平均水平的特征,然后在这些特征中再选择 信息增益比?最高的特征。?
2. ID3 只能处理离散变量,C4.5和CART可以处理连续变量
? ? ? ??其实ID3和C4.5处理连续变量本质上都是在连续的变量里面,找到切分点,把连续的属性转化成布尔类型,从而将连续醒变量转换多个取值区间的离散型变量(如果有N条样本,那么我们有N-1种离散化的方法:<=vj的分到左子树,>vj的分到右子树。计算这N-1种情况下最大的信息增益率。)另外,对于连续属性先进行排序(升序),只有在决策属性(即分类发生了变化)发生改变的地方才需要切开,这可以显著减少运算量
????????C4.5对连续属性的处理:(和CART一样是二叉分裂)

? ? ? ? 反观CART:不管是分类还是回归
????????分类是计算现有特征对该数据集的基尼指数。此时对每一个特征A,对其可能取的每一个值a,根据样本点对A=a的测试为“是”或“否”将D分割成D1和D2两个子集,然后去计算这个A=a时对这个集合的基尼系数
? ? ? ? 回归是利用最小化损失函数去做:这里的切分变量和切分点不是一一对应的,先遍历j,然后在每个j上又去遍历s,例子:切分变量:年龄,切分点:从8岁到40岁,所以切分点就[8.40]。其实就是通过找到一个点j,使得当前这次区分,两边都获得比较小的损失函数
? ? ? ? 也就是说,无论是分类还是回归都会对特征进行二值化分,因此可以很好地适用于连续变量。
3. ID3和C4.5只能应用于分类任务,CART分类回归都可以
????????主要原因是特征分裂的评价标准不一样,CART有两种评价标准:最小化平方误差和Gini系数。而ID3和C4.5的评价基础都是信息熵。
????????信息熵和Gini系数是针对分类任务的指标,而最小化平方误差是针对连续值的指标因此可以用来做回归,预测值等于该节点所有值的平均。
4. C4.5 和 CART都怎么处理缺失值的
????????机器学习笔记(7)——C4.5决策树中的缺失值处理_小赵的博客-CSDN博客_c4.5处理缺失值
? ? ? ? 没看懂,先放着,后期来看。
5. ID3 和C4.5可以在每个节点上产生出多叉分支,且每个特征在层级间不会复用,而CART每个节点只会产生出两个分支,每个特征可以被重复使用。
????????特征能否继续使用这样的问题应该转化为在当前分支下,该特征能否可再次划分的问题(或是是否还有可利用的价值)不能再次划分的意思就是在当前分支内,该特征只有唯一的值。
????????如果Xi是离散特征:
????????ID3和C4.5在离散特征上都是多叉树,就是按照该特征的全部特征值进行分裂,那么显然分裂后的任意一个分支内特征Xi只有唯一的值,所以该特征消耗掉了。(我用ID3和C4.5去选出对信息熵来说最优的特征,然后就全用了,这里应该上一个例子)
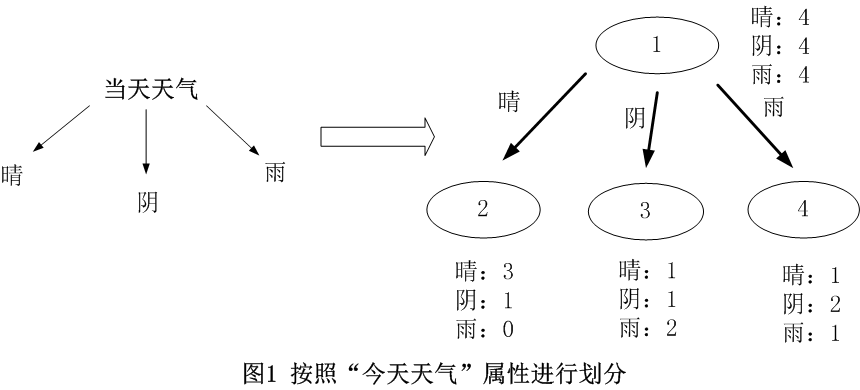 ?
?
????????如果Xi是连续特征:
????????ID3没法处理,略过。C4.5是将连续特征进行排序,按照相邻离散值的中点进行分裂,可以说在连续特征上,C4.5是二叉分裂的。如果该连续特征只有两个离散值,那么一次分裂就会消耗掉这个特征;如果有多个离散值,那么可以经受多次分裂。
????????最后再说CART算法:
????????CART算法是二叉树,也就是无论Xi是连续特征还是离散特征都是二叉分裂的。那么如果Xi有多于2个离散值,即便Xi是离散特征,也可以经受多次分裂,也就是你说的能被重复利用。
? ? ? ? 出自:CART算法中某一特征被使用后还能被重复使用吗? - 知乎
?
6. ID3和C4.5 可以通过剪枝来衡量树的准确率和泛化能力,CART直接利用全部数据发现所有可能的树结构进行对比。
? ? ? ? 具体的剪枝可以看以前的文章,里面有ID3,C4.5 以及 CART树 对应的剪枝流程: