[人工智能] FCOSR: A Simple Anchor-free Rotated Detector for Aerial Object Detection阅读笔记

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> FCOSR: A Simple Anchor-free Rotated Detector for Aerial Object Detection阅读笔记 -> 正文阅读

[人工智能]FCOSR: A Simple Anchor-free Rotated Detector for Aerial Object Detection阅读笔记

FCOSR论文阅读笔记

(一) Title

在这里插入图片描述
论文地址:https://arxiv.org/abs/2111.10780
项目地址:https://github.com/lzh420202/FCOSR

(二) Summary

研究背景:

现有的基于anchor-based方法的旋转框检测算法需要手动设置预设框,引入了额外的超参数和计算。基于anchor-free的方法通常具有复杂的体系结构,不容易部署。

本文方法:

本文提出了一个一阶段的带有角度旋转的检测框架FCOSR,一看就是基于FCOS架构,并且将二维高斯分布也引入进来了。这个工作主要关注的是在训练过程中的label assignment策略，包括：

采用ellipse center sampling方法来给旋转框(oriented bounding boxes)定义一个合适的采样区间
对于overlapping的目标区域，通过fuzzy sample assignment提供了一个更加合理的标签。
通过multi-level sampling模块解决了不充分采样的问题。

实验效果:

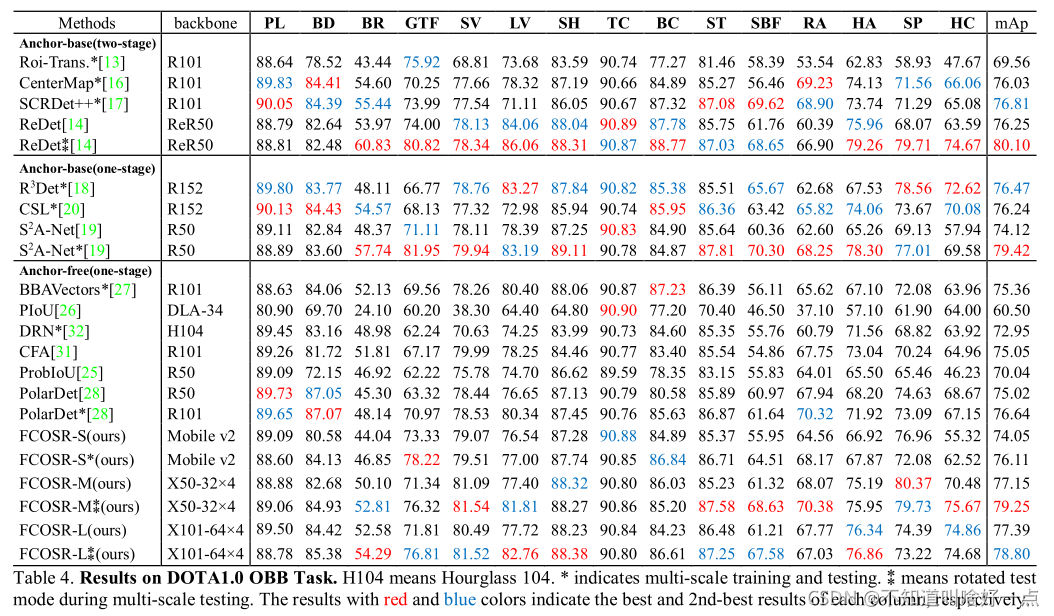
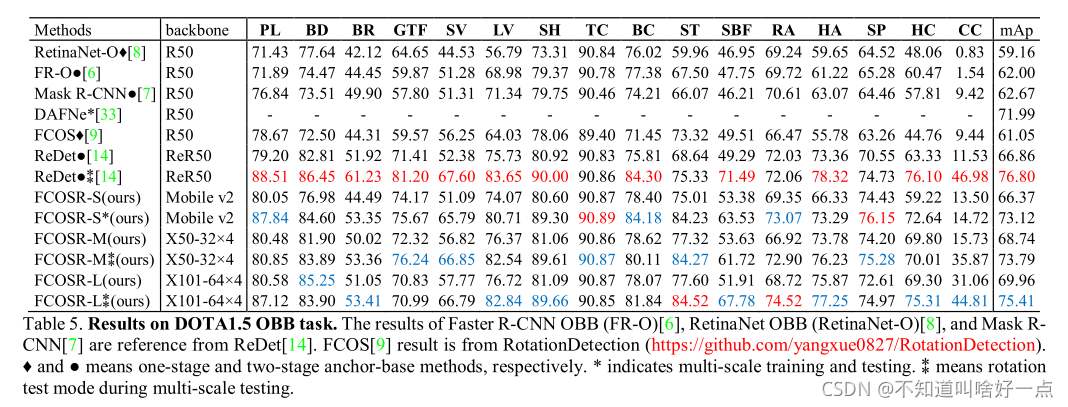
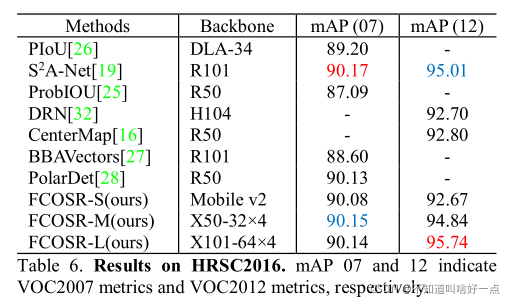
算法在DOTA1.0，DOTA1.5以及HRSC2016数据集上的map分别为79.27,75.41以及90.15。FCOSR在one-stage中优于其他的目标检测器。
将一个轻量网络转换成TensorRT格式,在Jetson Xavier NX上进行部署，在DOTAv1上10.68FPS,实现了73.93的mAP.

(三) Method

在这里插入图片描述
网络基于FCOS架构，直接预测中心点,长宽以及旋转角度。通过label assignment module定义特征图的输出，去掉了centerness分支。

3.1 网络输出

输出两个分支，分类分支是一个 $C$ 维的类别向量，回归分支包括一个5维的向量，这个5维向量的符号表示为 $(Reg_x,Reg_y,Reg_w,Reg_h,Reg_\theta)$ ,需要经过变换得到最终边界框 $offset_x,offset_y,w,h,angle)$ ，并且对边界框的要求是偏移量可以是负数，宽和高必须是正数，角度范围必须限制在0-90。将回归分支输出变换到最终边界框的计算公式为：
$\begin{array}{l} \text { offset }_{x y}=\operatorname{Reg}_{x y} \cdot k \cdot s \\ w h=\left(\operatorname{Elu}\left(\operatorname{Reg}_{w h} \cdot k\right)+1\right) \cdot s \\ \theta=\operatorname{Mod}\left(\operatorname{Reg}_{\theta}, \pi / 2\right) \end{array}$

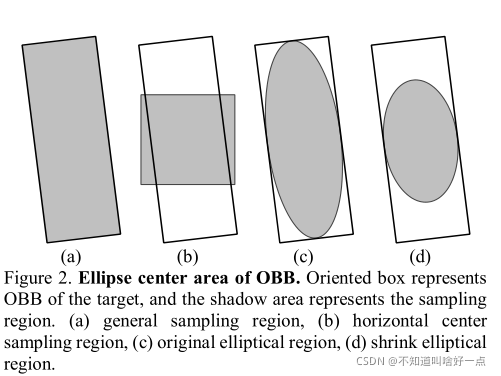
3.2 椭圆中心采样

Center Sampling是将采样点集中到目标中心附近,有助于减少低质量预测,提高模型性能。在FCOS以及YOLOX中都采用该策略提升了精度。然而将水平中心采样策略直接迁移到旋转框中存在着两个问题：

水平框的采样区域通常为 $\times 3$ 或者 $\times 5$ 的正方形,旋转框的角度会影响采样范围
对于长宽比较大的边界框来说，短边限制了中心采样的范围，这里我觉得是中心采样范围过大，会超出边界框。

为了解决上面两个问题，本文提出了基于二维高斯分布的椭圆中心采样方法,基于旋转框参数定义一个二维的高斯分布：
$\begin{aligned} \Sigma &=R_{\theta} \cdot \Sigma_{0} \cdot R_{\theta}^{I} \\ \mu &=(c x, c y) \\ R_{\theta} &=\left[\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right], \Sigma_{0}=\frac{1}{12}\left[\begin{array}{cc} w^{2} & 0 \\ 0 & h^{2} \end{array}\right] \end{aligned}$
其中 $\Sigma$ 是协方差矩阵,当角度为0时 $\Sigma_0$ 也是协方差矩阵， $\mu$ 是均值, $R_\theta$ 是旋转变换矩阵。正常情况下的二维高斯分布概率密度函数为：
$f(X)=\frac{1}{2 \pi|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(X-\mu)^{T} \Sigma^{-1}(X-\mu)\right)$
$X$ 表示二维坐标,将归一化项去掉得到：
$g(X)=\exp \left(-\frac{1}{2}(X-\mu)^{T} \Sigma^{-1}(X-\mu)\right)$
椭圆的2D高斯分布表示为 $g (X) = C$ 进行表示,当 $C=C_{0}=\exp (-1.5)$ 时,椭圆的等高线刚刚好能够切到旋转框上，也就是如下图中 $(c)$ 所示。随着 $C$ 的减小,椭圆曲线的范围将扩大。
当 $C$ 的范围在 $C_0,1]$ 直接时,就是一个缩放的椭圆核，这个椭圆核不超过边界框的范围 $C = 1$ 时就是中心点。此时不再采用图 $(a)$ 中的方式来确定正样本,而是通过判断点是否在椭圆内,在椭圆内的话就是正样本，不在椭圆内的话就是负样本。
接着解决第二个问题，长宽比较大时,二维高斯核的长边部分会距离图像中心很远，此时样本的可信度也比较小,通过调整长边高斯核方差来实现椭圆在长边方向上的收缩，也就是如上图中的 $(d)$ 所示。这里通过调整协方差矩阵来实现对长边的收缩：
$\Sigma_{0}=\frac{\min (w, h)}{12}\left[\begin{array}{ll} w & 0 \\ 0 & h \end{array}\right]$
也就是将椭圆的长轴收缩成 $\sqrt{wh}$ ,短边保持不变。博主认为这个椭圆中心采样方法就是TTFNet中的一种特例。

3.3 Fuzzy sample label assignment

FCOS中将不同尺度的目标分配给具有不同步长的特征图来减少ambiguous样本。对于尺度相近的目标，FCOS将ambiguous样本标签设置成smaller targets,也就是较小的目标(这里的大小说的是面积)，但是这种方式很难处理航空场景。这里将二维高斯分布的值看成是采样点到目标中心的距离度量，中心距离的度量通过下式表示：
$J(X)=\sqrt{w h} \cdot f(X)$
对于任何一个采样点,计算每一个采样点的 $J (X)$ 值,这个值越大表示越接近目标。按照当前的分配方式可以表述成：

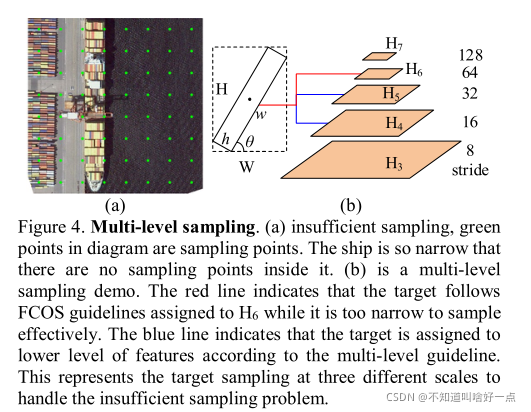
3.4 多阶段采样

对于大长宽比目标,按照上述方式,采样数量主要受短边的影响，当feature map的步长比采样区域更大时(受短边影响,虽然边界框很大,但是采样区域面积比较小,当比特征图的步长还小时就没法分配到特征点来回归边界框了),为了解决这个问题,本文通过比较短边和步长来决定是否在低层特征图中分配标签，满足下面两个条件的话就分配：

目标的短边同feature map步长的比值小于2,也就是在特征图上不超过4个点来回归目标。
旋转框最小的外界轴对齐矩形的长边超过了特征图的范围。
Multi-level sampling strategy允许我们将一些无法有效采样的目标添加到底层特征图上。在底层特征图上进行密集采样。

这里没说明是怎么将分配到下面的特征图上的，只说了什么情况下分配给下面的特征图。

3.5 损失函数

在分类损失中使用QFL,同时引入IoU来关联类别和边界框的质量：
$L(\sigma)=-|y-\sigma|^{\beta}((1-y) \log (1-\sigma)+y \log (\sigma))$
上式中 $y$ 表示IoU
回归损失使用ProbIoU loss。总损失表示为：
$\begin{aligned} L o s s &=\frac{1}{N_{p o s}} \sum_{z} Q F L+\\ & \frac{1}{\sum_{z} \mathbf{1}_{\left\{c_{z}^*>0\right\}} I o U} \cdot \sum_{z} \mathbf{1}_{\left\{c_{z}^*>0\right\}} I o U \cdot \operatorname{Loss}_{P r o b l o U} \end{aligned}$
其中 $N_{pos}$ 表示正样本数量， $\mathbf{1}_{\left\{c_{z}^*>0\right\}}$ 表示示性函数,博主觉得这里指的应该是在椭圆采样区域内的为1，不在这个区域的为0.

(四) Experiments

4.1 实验设置

数据集采用DOTA1.0，DOTA1.5以及HRSC2016,使用随机翻转+随机旋转增强数据。
使用ResNext50+FPN作为骨干,在DOTA上训练36个epoch，在HRSC2016上训练40k迭代。DOTA上使用SGD学习器，初始学习率0.01(感觉挺大的啊),学习率在24和33个epoch降低10倍。HRSC2016上使用SGD,学习率0.001在30K和36K学习率下降10倍。动量为0.9，权重衰减为0.0001.
提出使用两步旋转,第一步等概率旋转0，90，180，270.第2步以50%的概率旋转30和60度。这种两步旋转相比于随机旋转更好嘛？

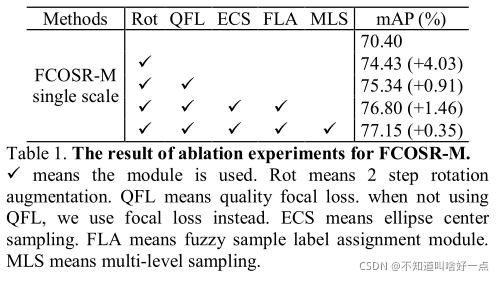
4.2 消融实验

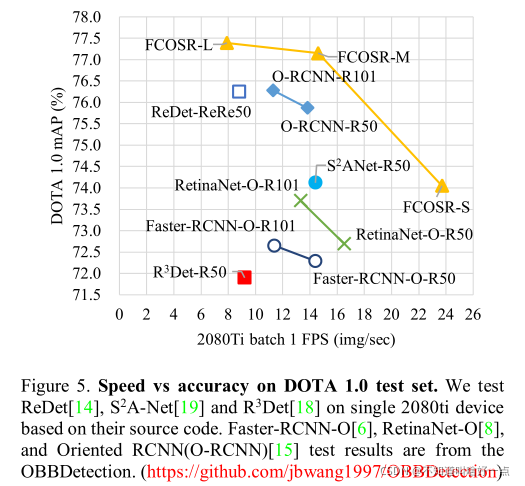
在这里插入图片描述

4.3 精度和速度

在这里插入图片描述

4.5 公开数据集上的对比实验

在这里插入图片描述

(五) Conclusions

本文将二维高斯分布引入到FCOS中，主要工作包括 ellipse center sampling, fuzzy sample label assignment, and multi-level sampling。椭圆中心采样为旋转对象提供了更合适的采样区域。模糊样本标签分配方法更合理地划分了重叠目标的采样区域。多层次抽样方法解决了大长宽比目标抽样不足的问题。

(六) Notes

8.1 主流的旋转框目标检测算法

带锚框的方法

ROI transformer:看着像Transformer,但是并不是基于Transformer架构的方法,主要是通过将ROI输出的水平proposals转变成OBB(旋转边界框),提取旋转proposal的特征用于后续的分类和回归。
ReDet中引入了一个rotation invariant卷积(e2cnn)到整个模型中,并且通过RiROI alignment提取了rotation invariant features
Oriented R-CNN中将ROI Transformer中的RROI learning 模块用一个轻量化，简单的oriented region proposal network(orientation RPN)进行替换
R3Det中通过Feature innovation module(FRM)模块水平的anchor进行微调得到旋转anchor
S2ANet由feature Alignment module(FAM)模块以及Oriented detection module(ODM)模块组成。FAM用于生成高质量的旋转anchor。ODM采用active filters来产生方向敏感和方向不变的特征，缓解分类分数同localization精度不一致的问题。
CSL将角度预测转换成分类任务,解决了discontinuous rotation angles的问题。
DCL中在CSL的基础上采用了密集编码来提高训练速度，同时采用角度距离和长宽比加权来改善性能。

无锚框方法

IENet采用了一个带有注意力机制的branch interactive module，能够融合分类和回归分支的特征。
GWD,KLD,ProbIoU使用两个二维高斯分布之间的距离度量来表示损失，给基于anchor-free的方式提供了一种新的回归损失方案。这个需要后面看看
PIoU定义了用于旋转框的能够梯度反向传播的损失函数
BBAVectors和PolarDet分别使用bbav vector以及polar coordinates定义旋转框
CenterRot使用可变形卷积来融合多尺度特征。
AROA采用了注意力机制。