总的参考:https://datawhalechina.github.io/unusual-deep-learning/
Task04 CNN
1、卷积
2、CNN基本原理
3、经典CNN
4、CNN主要应用
参考:
感觉课程讲述的很清楚,在记录基本笔记的情况下,记录一下从网上其它地方写的介绍。力求笔记尽可能简单移动,且简洁。
关于为什么要从全连接网络转到CNN这种权值共享的网络,主要有以下几点:
- 全连接网络,参数多,CNN网络的权值共享策略能够减少参数的数量
- 其次,全连接网络,不能够识别一些边缘信息,CNN网络能够通过对原始图片数据取padding来检测到原始数据的边缘信息。
- 卷积神经网络,可以通过核卷积操作进行尺度缩放,平移,旋转等操作,不影响其语义信息(教程中提及)
此外,卷积神经网络,引入了生物学中的感受野概念。
关于感受野感念,以及最后VGGNet中提及到的为什么2个感受野为3*3的卷积核比一个 5 * 5的卷积核要好,以及什么是感受野的串联?
在这个文章中有详细介绍到:
卷积神经网络中感受野的详细介绍_Microstrong-CSDN博客_感受野
简言之,感受野即卷积核在原来图片中占据的最大视野,一个卷积核囊括的最大面积。

图片来自:卷积神经网络(CNN)详解 - 知乎 (zhihu.com)
卷积:
卷积是数学中的卷积,关于卷积的一些性质,主要是关于无穷级数中常数项级数是否收敛的一些性质。比如:
1、正项级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un?收敛的充分必要条件是:它的部分核数列 { s n } \{s_n\} {sn?}有界。
2、比较审敛法,设 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un?和 ∑ n = 1 ∞ v n \sum_{n=1}^\infty v_n ∑n=1∞?vn? 都是正项级数,且 u n ≤ v n ( n = 1 , 2 , ? ? ) u_n \le v_n(n=1, 2,\cdots) un?≤vn?(n=1,2,?). 若级数 ∑ n = 1 ∞ v n \sum_{n=1}^\infty v_n ∑n=1∞?vn?收敛,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un?收敛;反之,若级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un?发散,则级数 ∑ n = 1 ∞ v n \sum_{n=1}^\infty v_n ∑n=1∞?vn?发散。
推论:
设 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un???和 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un???都是正项级数,如果级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un???收敛,且存在正正整数 N N N??,使当 n ≥ N n\ge N n≥N??时有 u n ≤ k v n ( k > 0 ) u_n \le k v_n(k>0) un?≤kvn?(k>0)??成立,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un???收敛;如果级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty} v_n ∑n=1∞?vn???发散,且当 n ≥ N n \ge N n≥N?? 时有 u n ≥ k v n ( k > 0 ) u_n \ge k v_n(k>0) un?≥kvn?(k>0)??成立,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un????发散。
3、比较审敛的极限形式,设 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un??和 ∑ n = 1 ∞ v n \sum_{n=1}^\infty v_n ∑n=1∞?vn??都是正项级数,
(1)如果 lim ? n → ∞ u n v n = l ( 0 ≤ l < ∞ ) \lim_{n \to \infty} \cfrac{u_n}{v_n}=l(0 \le l< \infty) limn→∞?vn?un??=l(0≤l<∞),且级数 ∑ n = 1 ∞ v n \sum_{n=1}^\infty v_n ∑n=1∞?vn?收敛,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un?收敛
(2)如果 lim ? n → ∞ u n v n = l > 0 \lim_{n \to \infty} \cfrac{u_n}{v_n} = l > 0 limn→∞?vn?un??=l>0?或 lim ? n → ∞ u n v n = + ∞ \lim_{n \to \infty} \cfrac{u_n}{v_n} = + \infty limn→∞?vn?un??=+∞?, 且级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty} v_n ∑n=1∞?vn?? 发散,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^\infty u_n ∑n=1∞?un??发散
4、比较审敛法:设
∑
n
=
1
∞
u
n
\sum_{n=1}^\infty u_n
∑n=1∞?un?为正项级数,如果
lim
?
n
→
∞
u
n
+
1
u
n
=
ρ
\lim_{n \to \infty}\cfrac{u_{n+1}}{u_n} = \rho
n→∞lim?un?un+1??=ρ
则当
ρ
<
1
\rho < 1
ρ<1时级数收敛;
ρ
>
1
\rho > 1
ρ>1(或
lim
?
n
→
∞
u
n
+
1
u
n
=
∞
\lim_{n \to \infty} \cfrac{u_{n+1}}{u_n}=\infty
limn→∞?un?un+1??=∞时级数发散;
ρ
=
1
\rho=1
ρ=1时级数可能收敛也可能发散。
5、极值审敛法,柯西判别法;设
∑
n
=
1
∞
u
n
\sum_{n=1}^{\infty} u_n
∑n=1∞?un?为正项级数,如果
KaTeX parse error: Undefined control sequence: \ at position 21: …_{n \to \infty}\? ?
6、TODO待补充
这里的卷积,其实可以很简单理解,一个是现在的数据,一个是过去t个时刻的数据。
关于卷积中padding的大小,可以分为窄卷积、宽卷积、等宽卷积,其中padding分别取值为0, K-1, (K - 1) / 2. 现在卷积一般是等宽卷积。
关于卷积如何在原始数据上起作用,是在原来的感知野中,以stride步长来进行滑动,原始图片深度是多少,就会有多少个这样的卷积核来作用到原来的数据(图片)中。这么说,想强调的是,卷积核的深度跟其作用的深度是一样的,各个深度下的权重共享(包括权重和偏置)是相等的,但是不同深度的权重共享是不同的。
其它卷积
转置卷积:讲地位特征映射到高维特征上。也就是说,讲原始特征中的感知野变“稀疏” , 对原始低维数据padding,进而得到相对”较大“的原始数据(图片),尽管在我们看来,原始数据经过这样扩充之后是很”稀疏“的。
空洞卷积:为了增加输出单元的视野,通过给卷积核插入”空洞“来相对增加其大小。
不同于转置卷积,这里的话,是忽略中间的一些单元(维度),进而达到稀疏(扩大视野)的作用。
卷积神经网络的原理:
卷积层、激活函数、汇聚层、全连接层、输出层
卷积层,是对两个矩阵作卷积(主要是依赖当前的输出,以及对原始数据(图片)的华东)。
能够体现出两个矩阵之间的互相关作用
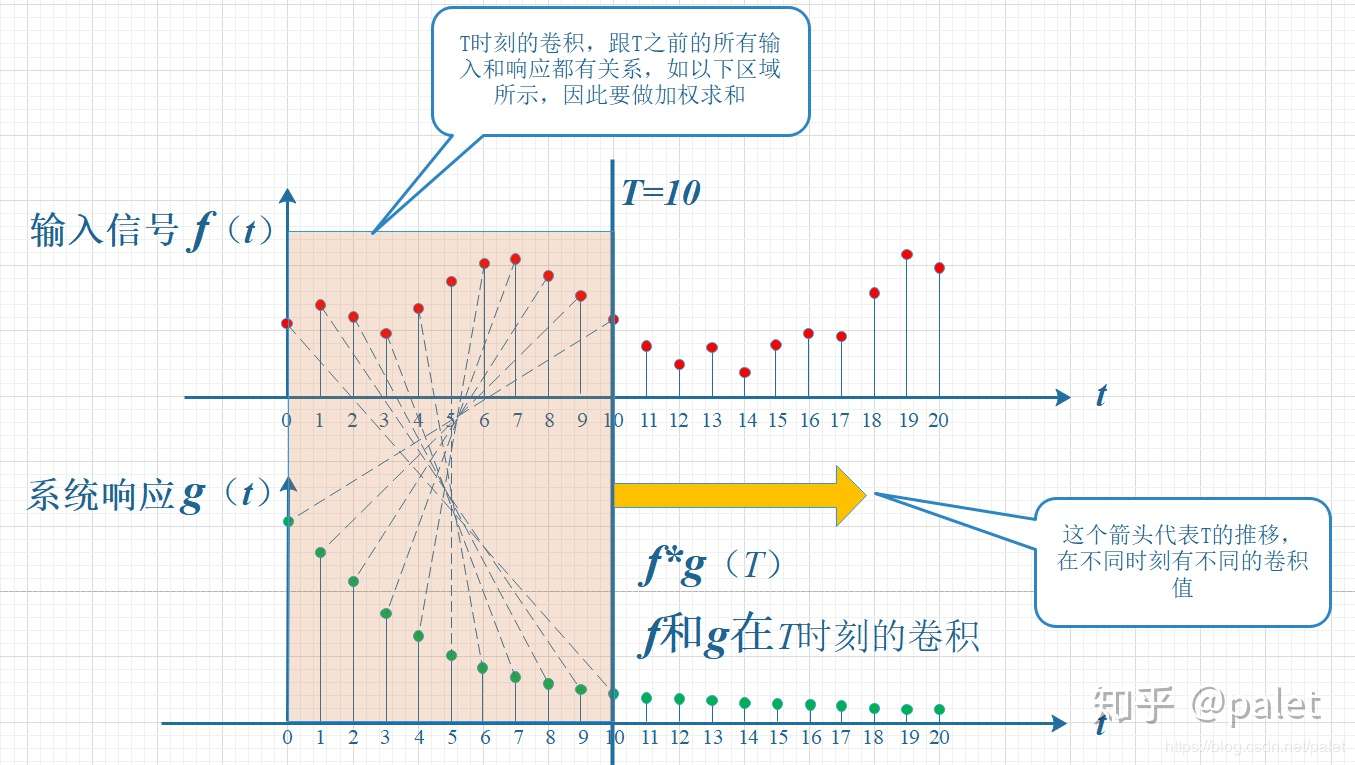 图片源自:如何通俗易懂地解释卷积? - palet的回答 - 知乎 https://www.zhihu.com/question/22298352/answer/637156871
图片源自:如何通俗易懂地解释卷积? - palet的回答 - 知乎 https://www.zhihu.com/question/22298352/answer/637156871
就类似于交互作用吧。交叉的意思。
卷积步长:Stride
卷积kenerl的宽度核高度:Width, Height
补全:padding
深度:channel的个数,卷积核的深度要和其作用的数据(图片)的深度一致。最后输出的数据(图片)的深度跟当前卷积核的个数(K)有关。
输出的维度
H
2
=
H
1
?
f
+
2
?
p
S
+
1
W
2
=
W
1
?
f
+
2
?
p
S
+
1
D
2
=
D
1
\begin{aligned} H_2 &= \cfrac{H_1 - f + 2 * p}{S} + 1\\ W_2 &= \cfrac{W_1 - f + 2 * p}{S} + 1\\ D_2 &= D_1 \end{aligned}
H2?W2?D2??=SH1??f+2?p?+1=SW1??f+2?p?+1=D1??
感受野:前面有提及。
激活函数:一般取ReLU, 为了避免ReLU的dead units, 设置一个较小的学习率。或者说设置PReLU, ELU,
特征图:未具体了解:TODO
池化层
也称为汇聚层。将原始的数据通过取min, max, average汇聚到一起(原始数据的宽度核高度变小)。
作用:
- 汇聚信息,减少噪声影响,进而防止过拟合。
- 增强鲁棒性。
全连接
降维特征输出图
输出层:
使用softmax或者加权求和得到线性输出(例如要预测某个物体所在的位置)。
CNN的训练
整体的流程是跟一般的神经网络是类似的。
前向,计算损失,梯度(误差),反向传播更新参数,继续前向,。。。,来回,直到满足停止条件。
这里实际的计算,因为引入的卷积,实际上变得比较复杂,具体如何,还需要继续研究参考文献[1]和[2], 前者讲述公式的具体训练流程,后者讲述将卷积层转化为全连接层。具体细节,还待我继续研究总结。TODO
经典卷积神经网络
1、LeNet-5,主要学习网络结构,核的大小的改变,以及卷积核的个数改变。突出:参数数量较多。
2、AlexNet, 主要学习将每一层的卷积核分开来,分别使用两次卷积,再进行类似于全连接的那种连接,进而得到一种并行,快速计算的效果。
这个是mobile net吗?是为了降低模型复杂度的,让模型快速运行的吗?TODO
3、VGGNet, 使用两个卷积核(+Relu),对应一个池化层,三个卷积核(+Relu)对应一个池化层,最后全连接层(+ReLU,Dropout),得到最终输出。
富有结构化的网络,使用多层串联的小卷积层来代替原来一个”大“卷积层。
4、Inception Net:引入了1 * 1卷积核。
5、ReNet,引入上个输出,作为残差,记忆上一步的信息。解决因为深度过大带来的梯度爆炸和梯度消失的问题。
6、
Densenet, 保留原来每个时刻的信息,传到下面的网络中去,以一种全连接的方式。
参考
[1] 零基础入门深度学习(4) - 卷积神经网络 - 作业部落 Cmd Markdown 编辑阅读器 (zybuluo.com) 讲的很细致,关于如何反向传播求导那块,以及由代码的展示
[2] 卷积神经网络(CNN)详解 - 知乎 (zhihu.com) 讲的稍微啰嗦,不过也很细致,关于感受野,以及一般的Filter取值、S(Stride),P(padding)取值有详细介绍
[3] 详解卷积神经网络(CNN)_liuhe_的博客-CSDN博客
[4] 一文让你理解什么是卷积神经网络 - 简书 (jianshu.com)
[5] AI学习笔记——卷积神经网络(CNN) - 简书 (jianshu.com) 入门很好,最后一个图片,可以使用特定的卷积核来识别图像中的轮廓(竖直或者垂直的)