[人工智能]Datawhale~水很深的深度学习~Task 4: 卷积神经网络（CNN）

写在前面?
\quad\quad 本系列笔记为Datawhale11月组队学习的学习笔记：水很深的深度学习。本次组队学习重理论知识学习，包含DL相关的基础知识，如CNN、RNN、Transformer等。参与本次组队学习两个目的：第一，提起自己DL学习的热情；第二，巩固基础知识，使得做实验更加得心应手。
\quad\quad DW 学习文档：由于文档所给出的部分比较完善，因此以下笔记是在原文档的基础上，增加自己理解和补充的产物，好好学习，天天向上！

卷积神经网络

本章内容是对于卷积神经网络的总结。卷积神经网络（CNN）的核心内容是kernel(卷积核)，其最重要的特征是：平移不变性和参数共享。在下文的理解过程中，可以将卷积核理解为“特征提取器”，且一次卷积的结果为提取之后的特征。

回顾全连接神经网络，如下图，它的权重矩阵的参数非常多。

而且往往自然图像中的物体都具有局部不变性特征，即尺度缩放、平移、旋转等操作不影响其语义信息，但是全连接前馈网络很难提取这些局部不变特征，这就引出了我们将要介绍的卷积神经网络（Convolutional Neural Networks，CNN）。

卷积神经网络也是一种前馈神经网络，是受到生物学上感受野（感受野主要是指听觉系统、本体感觉系统和视觉系统中神经元的一些性质）的机制而提出的（在视觉神经系统中，一个神经元的感受野是指视网膜上的特定区域，只有这个区域内的刺激才能够激活该神经元）。

I CNN基本原理

卷积神经网络的基本结构大致包括：卷积层、激活函数、池化层、全连接层、输出层等。

1.1 卷积基本介绍

卷积：$(f?g)(n)$称为 $f$ 和 $g$ 的卷积，连续卷积和离散卷积可以表达为如下形式：
$$\begin{gathered} (f?g)(n)={\int }_{?\infty }^{\infty }f(\tau )g(n?\tau )d\tau \\ (f?g)(n)=\sum _{\tau =?\infty }^{\infty }f(\tau )g(n?\tau ) \end{gathered}$$

上述公式为高数中学到的卷积，参考知乎的问题–如何通俗易懂地解释卷积？，让我们来通俗易懂地理解一下卷积~
卷积在数学上的操作分为两步：卷和积。卷：将g函数沿着坐标轴从右翻转到左；积：将g函数和f函数对应位置乘积求和。

卷积有很多应用，经常用于处理一个输入，通过系统产生一个适应需求的输出。

• 统计学中加权平均法
• 概率论中两个独立变量之和概率密度的计算
• 信号处理中的线性系统
• 物理学的线性系统
• 图像处理中的应用(卷积神经网络)

卷积经常用在信号处理中，用于计算信号的延迟累积。

例如，假设一个信号发生器每个时刻 $t$ 产生一个信号 $x_t$ ，其信息的衰减率为 $w_k$ ，即在 $k?1$ 个时间步长后，信息为原来的 $w_k$ 倍，假设 $w_1=1,w_2=1/2,w_3=1/4$，则时刻 $t$ 收到的信号 $y_t$ 为当前时刻产生的信息和以前时刻延迟信息的叠加，即：
$$\begin{array}{rl}{y}_t& =1\times x_t+1/2\times x_{t?1}+1/4\times x_{t?2}\\ & =w_1\times x_t+w_2\times x_{t?1}+w_3\times x_{t?2}\\ & =\sum _{k=1}^3{w}_k?x_{t?k+1}\end{array}$$
其中 $w_k$ 就是滤波器，也就是常说的卷积核 convolution kernel。

给定一个输入信号序列 $x$ 和滤波器 $w$，卷积的输出为：
$$y_t=\sum _{k=1}^K{w}_k{x}_{t?k+1}$$
不同的滤波器来提取信号序列中的不同特征：

下面引入滤波器的滑动步长S和零填充P：

卷积的结果按输出长度不同可以分为三类：

1. 窄卷积：步长 𝑇 = 1 ，两端不补零 𝑃 = 0 ，卷积后输出长度为 𝑀 ? 𝐾 + 1
2. 宽卷积：步长 𝑇 = 1 ，两端补零 𝑃 = 𝐾 ? 1 ，卷积后输出长度 𝑀 + 𝐾 ? 1
3. 等宽卷积：步长 𝑇 = 1 ，两端补零 𝑃 =(𝐾 ? 1)/2 ，卷积后输出长度 𝑀

在早期的文献中，卷积一般默认为窄卷积。而目前的文献中，卷积一般默认为等宽卷积。

在图像处理中，图像是以二维矩阵的形式输入到神经网络中，因此我们需要二维卷积。下面给出定义：一个输入信息 $X$ 和滤波器 $W$ 的二维卷积为 $Y=W?X$，即 $y_{ij}={\sum }_{u=1}^U{\sum }_{v=1}V{w}_{uv}{x}_{i?u+1,j?v+1}$ .可以参考下面的算例。

下图直接表示卷积层的映射关系

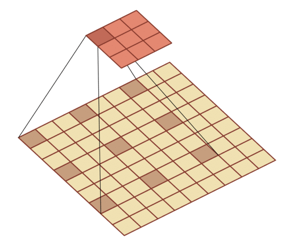
多个卷积核的情况：下图是表示步长2、filter 3*3 、filter个数6、零填充 1的情形。

几乎很多实际应用都可以对应到这个问题上，都是在做这样一件事

1）输入对应着rgb图片

2）一旦输入的特征图个数是多个，这个时候每一组filter就应该是多个，而这里有两组filter

3）输入是三个特征图，输出为两个特征图，那么我们同样看看每个特征图怎么计算的。

典型的卷积层为3维结构

1.2 卷积层

二维卷积运算：给定二维的图像I作为输入，二维卷积核K，卷积运算可表示为 $S(i,j)=(I?K)(i,j)={\sum }_m{\sum }_{n}I(i?m,j?n)K(m,n)$，卷积核需要进行上下翻转和左右反转
$$S(i,j)=\mathrm{sum}?\begin{array}{ccc}I(i?2,j?2)& I(i?2,j?1)& I(i?2,j)\\ I(i?1,j?2)& I(i?1,j?1)& I(i?1,j)\\ I(i,j?2)& I(i,j?1)& I(i,j)\end{array}?.??\begin{array}{rll}K(2,2)& K(2,1)& K(2,0)\\ K(1,2)& K(1,1)& K(1,0)\\ K(0,2)& K(0,1)& K(0,0)\end{array}??$$
卷积实际上就是互相关

卷积的步长(stride)：卷积核移动的步长

卷积的模式：Full、Same和Valid

数据填充：如果我们有一个 𝑛×𝑛 的图像，使用𝑓×𝑓 的卷积核进行卷积操作，在进行卷积操作之前我们在图像周围填充 𝑝 层数据，输出的维度：

感受野：卷积神经网络每一层输出的特征图(featuremap)上的像素点在输 入图片上映射的区域大小，即特征图上的一个点对应输入图上的区 域。

那么如何计算感受野的大小，可以采用从后往前逐层的计算方法：

• 第 i 层的感受野大小和第 *i-*1 层的卷积核大小和步长有关系，同时也与第 (*i-*1)层感受野大小有关
• 假设最后一层(卷积层或池化层)输出特征图感受野的大小(相对于其直 接输入而言)等于卷积核的大小

卷积层的深度(卷积核个数)：一个卷积层通常包含多个尺寸一致的卷积核

1.3 激活函数

激活函数是用来加入非线性因素，提高网络表达能力，卷积神经网络中最常用的是ReLU，Sigmoid使用较少。

1. ReLU函数
$$f(x)=\{\begin{array}{l}0,x<0\\ x,x\ge 0\end{array}$$
ReLU函数的优点：

• 计算速度快，ReLU函数只有线性关系，比Sigmoid和Tanh要快很多
• 输入为正数的时候，不存在梯度消失问题

ReLU函数的缺点：

• 强制性把负值置为0，可能丢掉一些特征
• 当输入为负数时，权重无法更新，导致“神经元死亡”(学习率不 要太大)

2. Parametric ReLU
$$f(x)=\{\begin{array}{l}\alpha x,x<0\\ x,x\ge 0\end{array}$$

• 当 𝛼=0.01 时，称作Leaky ReLU
• 当 𝛼 从高斯分布中随机产生时，称为Randomized ReLU(RReLU)

PReLU函数的优点：

• 比sigmoid/tanh收敛快
• 解决了ReLU的“神经元死亡”问题

PReLU函数的缺点：需要再学习一个参数，工作量变大

3. ELU函数
$$f(x)=\{\begin{array}{l}\alpha (e^x?1),x<0\\ x,x\ge 0\end{array}$$
ELU函数的优点：

• 处理含有噪声的数据有优势
• 更容易收敛

ELU函数的缺点：计算量较大，收敛速度较慢

• CNN在卷积层尽量不要使用Sigmoid和Tanh，将导致梯度消失。
• 首先选用ReLU，使用较小的学习率，以免造成神经元死亡的情况。
• 如果ReLU失效，考虑使用Leaky ReLU、PReLU、ELU或者Maxout，此时一般情况都可以解决

特征图

• 浅层卷积层：提取的是图像基本特征，如边缘、方向和纹理等特征
• 深层卷积层：提取的是图像高阶特征，出现了高层语义模式，如“车轮”、“人脸”等特征

1.4 池化层

池化操作使用某位置相邻输出的总体统计特征作为该位置 的输出，常用最大池化**(max-pooling)和均值池化(average- pooling)**。

池化层不包含需要训练学习的参数，仅需指定池化操作的核大小、操作步幅以及池化类型。

池化的作用：

• 减少网络中的参数计算量，从而遏制过拟合
• 增强网络对输入图像中的小变形、扭曲、平移的鲁棒性(输入里的微 小扭曲不会改变池化输出——因为我们在局部邻域已经取了最大值/ 平均值)
• 帮助我们获得不因尺寸而改变的等效图片表征。这非常有用，因为 这样我们就可以探测到图片里的物体，不管它在哪个位置

1.5 全连接层

• 对卷积层和池化层输出的特征图(二维)进行降维
• 将学到的特征表示映射到样本标记空间的作用

1.6 输出层

对于分类问题：使用Softmax函数
$$y_i=\frac{e^{z_i}}{{\sum }_{i=1}^n{e}^{z_i}}$$
对于回归问题：使用线性函数
$$y_i=\sum _{m=1}^M{w}_{im}{x}_m$$

1.7 卷积神经网络的训练

Step 1：用随机数初始化所有的卷积核和参数/权重

Step 2：将训练图片作为输入，执行前向步骤(卷积， ReLU，池化以及全连接层的前向传播)并计算每个类别的对应输出概率。

Step 3：计算输出层的总误差

Step 4：反向传播算法计算误差相对于所有权重的梯度，并用梯度下降法更新所有的卷积核和参数/权重的值，以使输出误差最小化

注：卷积核个数、卷积核尺寸、网络架构这些参数，是在 Step 1 之前就已经固定的，且不会在训练过程中改变——只有卷 积核矩阵和神经元权重会更新。

和多层神经网络一样，卷积神经网络中的参数训练也是使用误差反向传播算法，关于池化层的训练，需要再提一下，是将池化层改为多层神经网络的形式

将卷积层也改为多层神经网络的形式

II 经典CNN网络

• LeNet-5：1998年提出，主要进行手写数字识别和英文字母识别。经典的卷积神经网络，LeNet虽小，各模块齐全，是学习 CNN的基础。
• AlexNet：2012年提出，获得ImageNet LSVRC-2012(物体识别挑战赛)的冠军，1000个类别120万幅高清图像（Error: 26.2%(2011) →15.3%(2012)），通过AlexNet确定了CNN在计算机视觉领域的王者地位。
• VGGNet
• Inception
• ResNet：解决了瓶颈问题。随着卷积网络层数的增加，误差的逆传播过程中存在的梯度消失和梯度爆炸问题同样也会导致模型的训练难以进行，甚至会出现随着网络深度的加深，模型在训练集上的训练误差会出现先降低再升高的现象。残差网络的引入则有助于解决梯度消失和梯度爆炸问题。

III 新型CNN网络

deformable 可变形卷积
扩张（膨胀）卷积
三维卷积

转置卷积/微步卷积：低维特征映射到高维特征

空洞卷积：为了增加输出单元的感受野，通过给卷积核插入“空洞”来变相地增加其大小。

IV 主要应用

CNNs的应用领域主要集中在图像领域、语音类、NLP领域等，一般针对的任务类型为欧式空间的任务，如图片天然的结构就与卷积核一致，因此在图像分析领域，以下几种任务都可以用CNNs来建模：

• 图像分类(物体识别)：整幅图像的分类或识别
• 物体检测：检测图像中物体的位置进而识别物体
• 图像分割：对图像中的特定物体按边缘进行分割
• 图像回归：预测图像中物体组成部分的坐标

在NLP领域，如情感分析：分析文本体现的情感(正负向、正负中或多态度类型)。一般将文本进行编码（可以使用one-hot编码方式），然后进行特征嵌入，可以得到如下图左侧部分所示的标准张量，将其当作图片来看，使用CNN建模，即使用卷积核提取原文本特征。

语音类，一般是序列数据，也可以按照上述NLP的处理方式，先对原数据进行特征嵌入，将数据格式调整为$H\times W\times C$这种标准shape，即可使用CNN进行特征提取。然而，对于序列问题，考虑到顺序性，一般使用RNNs建模更为有效。

V 总结

本文从“卷积”的概念到CNN的基本构成成分的解释，包含经典的CNN模型以及解决的任务，此外我引申了一些变形/特殊的CNN模型，从浅层了解各种CNN的应用，以加深对CNNs的理解。

学习内容参考自：水很深的深度学习文档~CNN