[人工智能]深度学习-Non-local Neural Networks非局部神经网络

论文下载

0.概述

捕获长范围依赖在深度神经网络中具有核心重要性。对于顺序数据（例如，在语音、语言中），重复性的操作是远程依赖建模的主要解决方案。对于图像数据，长距离依赖性是由深层的卷积运算形成的大感受野建模的。卷积运算和循环运算都处理局部邻域，无论是在空间还是时间上；因此，只有重复应用这些操作，通过数据逐步传播信号，才能捕获长程依赖关系。重复本地操作有几个限制。

• 它的计算效率很低。
• 会导致需要仔细解决的优化困难。
• 这些挑战使得多跳依赖建模更加困难，例如当信息需要在遥远的位置之间来回传递时。

在本文中，我们将非本地操作(Non-local Operation)作为一种高效、简单和通用的组件，用于使用深度神经网络捕获远程依赖关系。我们提出的非局部运算是计算机视觉中经典非局部平均运算(Non-local Means)的推广。直观地说，非局部操作计算某个位置的响应，是通过计算输入特征映射中所有位置的特征的加权和。位置集可以在空间、时间或时空中，这意味着我们的操作适用于图像、序列和视频问题。
使用非局部运算有几个优点：

• 与循环运算和卷积运算的渐进行为相比，非局部运算通过计算任意两个位置之间的交互直接捕获长程依赖，而不管它们的位置距离如何；
• 正如我们在实验中所展示的，非局部操作是有效的，即使只有几层（例如5层），也能达到最佳效果；
• 最后，我们的非局部操作保持可变的输入大小，并且可以轻松地与其他操作（例如，我们将使用的卷积）组合。
  我们展示了非局部操作在视频分类应用中的有效性。在视频中，**空间和时间上的遥远像素之间会发生远距离交互。一个非局部块（我们的基本单元）可以以前馈方式直接捕获这些时空依赖关系。**对于一些非局部块，我们称之为非局部神经网络的架构比2D和3D卷积网络（包括膨胀变量）更准确地用于视频分类。此外，非局部神经网络比三维卷积神经网络在计算上更经济。在动力学和Charades数据集上介绍了全面的烧蚀研究。只使用RGB without any bells and whistles（例如，光流，多尺度测试），我们的方法在这两个数据集上都取得了与最新竞赛获胜者相当或更好的结果。
  为了证明非局部操作的通用性，我们进一步提出了目标检测/分割和姿态估计实验在COCO数据集。在强大的Mask R-CNN基线之上，我们的非局部块可以在很小的额外计算成本下提高所有三个任务的精度。结合视频上的证据，这些图像实验表明，非局部操作通常是有用的，可以成为设计深度神经网络的基本构件。

1.相关工作

1.1.Non-local image processing.（非局部影像处理）

非局部均值是一种经典的滤波算法，它计算图像中所有像素的加权平均值。它允许遥远的像素对基于patch外观相似性的位置的过滤响应做出贡献。这种非局部过滤的想法后来发展成BM3D(块匹配3D)，它对一组相似但非局部的patch进行过滤。与深度神经网络相比，BM3D是一种实心图像去噪基线。非局部匹配也是很多成功纹理合成，超分辨率和修复算法的本质。

1.2.Graphical models（图模型）

长期依赖关系可以通过图形模型来建模，例如条件随机场(CRF)。在深度神经网络的背景下，CRF可以被用于网络的后处理语义分割预测。CRF的迭代平均场推理可以转化为递归网络并进行训练。相比之下，我们的方法是一个更简单的前馈块计算非局部滤波。与这些用于分割的方法不同，我们的通用组件用于分类和检测。这些方法和我们的方法还涉及到一个更抽象的模型，称为图神经网络。

1.3.Feedforward modeling for sequences（对序列进行前馈建模）

最近出现了一种使用前馈(即非递归)网络建模语音和语言序列的趋势。在这些方法中，由非常深的一维卷积所贡献的大型接收字段捕获长期依赖项。这些前馈模型适合并行实现，并且比广泛使用的循环模型更有效。

1.4.Self-Attention（自注意力机制）

自我关注模块通过关注所有位置并在嵌入空间中取其加权平均值，计算序列中某个位置（例如，一个句子）的响应。正如我们将在下一篇文章中讨论的那样，自我关注可以被视为Non-local 平均值的一种形式，从这个意义上说，我们的工作将机器翻译的自我关注与适用于计算机视觉中图像和视频问题的更一般的非局部过滤操作联系起来。

1.5.Interaction Networks（交互网络）

交互网络（IN）最近被提出用于物理系统建模。它们在涉及成对交互的对象的图形上进行操作。Hoshen[23]在多智能体预测建模的背景下提出了Vertex Attention IN （顶点注意力交互网络）中更有效的顶点注意。另一个变量，命名为关系网络（Relation Networks），在其输入中的所有位置对特征嵌入计算函数。我们的方法也处理所有对，我们将在等式（1）中解释（f（xi，xj））。虽然我们的非局部网络与这些方法相联系，但我们的实验表明，该模型的非局部性，这是正交于注意/互动/关系的想法(例如，一个网络可以关注一个局部区域)，是其成功的关键。非局部建模是图像处理中一个长期的关键元素，在最近的计算机视觉神经网络中被大量忽略。

1.6.Video classification architectures（视频分类架构）

频分类的一种自然解决方案是结合cnn对图像的成功和rnn对序列的成功。相比之下，前馈模型是通过三维卷积(3D convolutions, C3D)在时空中实现的，三维滤波器可以通过“膨胀”预先训练的二维滤波器形成。除了在原始视频输入端到端建模之外，已经发现光流和轨迹是有用的。流和轨迹都是现成的模块，可以找到长期的、非局部的依赖关系。

2.Non-local 神经网络

我们首先给出非局部操作的一般定义，然后提供它的几个具体实例。

2.1.公式

按照非局部均值的定义，我们定义在深度神经网络中的non-local操作如下：

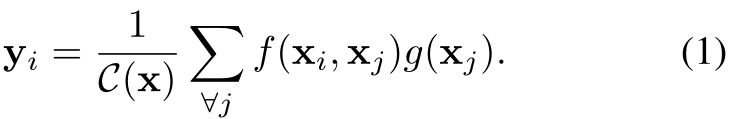
• x是输入信号，cv中使用的一般是feature map
• i 代表的是输出位置，如空间、时间或者时空的索引，他的响应应该对j进行枚举然后计算得到的
• f 函数式计算i和j的相似度
• g 函数计算feature map在j位置的表示
• 最终的y是通过响应因子C(x) 进行标准化处理以后得到的
  i代表的是当前位置的响应，j代表全局响应，通过加权得到一个非局部的响应值。
  f(xi,xj)用来计算i和所有可能关联的位置j之间pairwise的关系，这个关系可以是比如i和j的位置距离越远，f值越小，表示j位置对i影响越小。g(xj)用于计算输入信号在j位置的特征值。C(x)是归一化参数。
  在全连接层中（FC）x_j和x_i之间的关系不是输入数据的函数，是直接通过学习得到权重，而Non-local操作中，根据不同位置之间的关系计算响应。此外，我们在式(1)中的公式支持可变大小的输入，并保持相应的输出大小。相反，fcl层需要一个固定大小的输入/输出，并且失去了位置对应。非局部操作是一个灵活的构建块，可以轻松地与卷积/循环层一起使用。它可以添加到深度神经网络的早期部分，而不像通常在最后使用的fc层。这允许我们构建更丰富的层次结构，结合非局部和局部信息。

2.2 实例

接下来我们描述f和g的几个版本。有趣的是，我们将通过实验(Table2a)表明，我们的非局部模型对这些选择不敏感，这表明一般的非局部行为是观察到的改进的主要原因。为简单起见，我们只考虑线性嵌入的形式:g(x_j) =W_gx_j，其中W_g是一个需要学习的权重矩阵。这可以实现为 1×1空间卷积或1×1×1时空卷积。接下来我们讨论成对函数f的选择。

2.2.1.高斯

在非局部均值和双边滤波器之后，自然选择高斯函数。在本文中，我们考虑：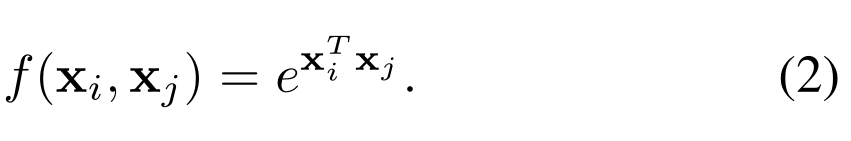
X^T _i X _j 为计算的点积相似性，标准化因子设置为C(x)=∑_∨j f(x_i ,x_j )

2.2.2.嵌入式高斯

高斯函数的简单扩展是在嵌入空间中计算相似性。在本文中，我们考虑：

θ(x_i)=W_θx_i和ф(x_j)=W_фx_j 是两个嵌入式，标准化因子设置为C(x)=∑_∨j f(x_i ,x_j )
self-attention模块其实就是non-local的embedded Gaussian版本的一种特殊情况。对于给定的i，C(x)f(x_i,x_j)就变成了计算所有j的softmax，即y=softmax(x^TW^T_θW_?x)g(x)，这就是self-attention的表达形式。这样我们就将self-attention模型和传统的非局部均值联系在了一起，并且将sequential self-attention network推广到了更具一般性的space/spacetime non-local network，可以在图像、视频识别任务中使用。

2.2.3.点乘

f也可以定义成点乘相似度，即：

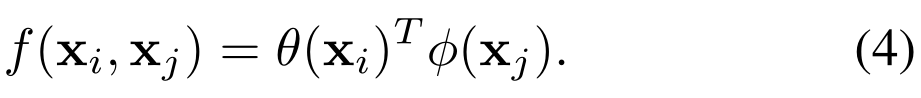
这里我们采用嵌入式版本。在这种情况下，我们设置归一化因子C(x)=N，其中N是x的总元素个数。规范化是必要的，因为输入可以具有可变的大小。点积和嵌入式高斯版本之间的主要区别在于softmax的存在，它起着激活函数的作用。

2.2.4.Concatenation

Concat是在Relation Networks 中用到的pairwise function。我们也给出了一个concat形式的f，如下：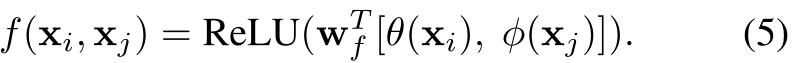
这里[.,.]表示的是concat，wf是能够将concat的向量转换成一个标量的权重向量。这里设置C(x)=N。
以上几个变体展示了我们通用非局部操作的灵活性。我们相信替代版本是可能的，并可能改善结果。

2.3.非局部块

我们将(1)式中的non-local操作变形成一个non-local block，以便其可以被插入到已有的结构中。
我们定义一个non-local block为：
其中y_i 由等式（1）给出，x_i 表示残差链接。残差连接允许我们将新的非局部块插入到任何预先训练的模型中，而不会破坏其初始行为。

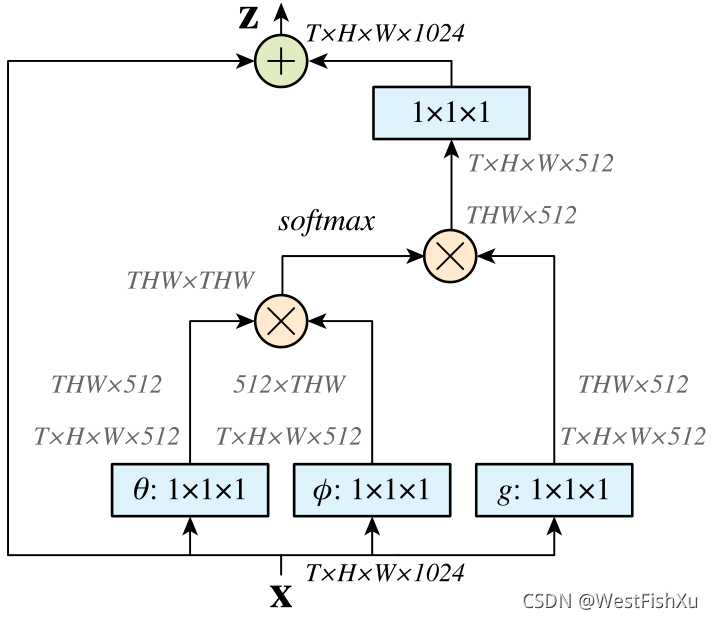
图2
时间空间非局部模块。特征图显示为其张量的形状T×H×W×1024用于1024个通道（注意时执行适当的整形）。“?” 表示矩阵乘法，和“⊕” 表示按元素求和。对每行执行softmax操作。蓝色框表示1×1×1卷积。这里我们显示了嵌入的高斯版本，瓶颈为512个通道。
普通高斯版本可以通过移除θ和φ来完成，点积版本可以通过用1/N的缩放替换softmax来完成.

图2中举例说明了一个非局部块。等式（2）、（3）或（4）中的成对计算可以简单地通过矩阵乘法完成，如图2所示；（5）中的连接版本很简单。非局部块的成对计算在用于高级次采样特征映射时是轻量级的。例如，图2中的典型值为T=4、H=W=14或7。通过矩阵乘法进行的成对计算可与标准网络中的典型卷积层进行比较。我们进一步采用以下实现，使其更加高效。
我们将W_g、W_θ和W_φ表示的通道数设置为x通道数的一半。这遵循了瓶颈设计，并将块的计算量减少了约一半。等式（6）中的权重矩阵W_zi计算y_i位置嵌入（position-wise embedding ），将通道数与x匹配。参见图2。子采样技巧可用于进一步减少计算量。我们将公式（1）修改为：yi=f(x_i,x^∧_j)g(x^∧_j)，其中x^∧是x的二次抽样版本（例如，通过池化操作）。我们在空间域中执行此操作，这可以将成对计算量减少1/4。这种技巧不会改变非局部行为，只会使计算变得更稀疏。这可以通过在φ和g图2之后添加最大池层来实现。我们将这些有效的修改用于本文研究的所有非局部块。
结合示意图（以Embeded Gaussian为例

• x代表feature map, xi代表的是当前关注位置的信息； xj代表的是全局信息。
• θ代表的是θ(xi)=Wθxi? ,实际操作是用一个1×1卷积进行学习的
• φ代表的是?(xj)=W?xj?,实际操作是用一个1×1卷积进行学习的
• g同理
• C(x)代表的是归一化操作，在embedding gaussian中使用的是Sigmoid实现的。
  non-local block的pairwise的计算可以是非常lightweight的，如果它用在高层级，较小的feature map上的话。比如，图2上的典型值是T=4，H=W=14 or 7。通过矩阵运算来计算parwise function的值就和计算一个conv layer的计算量类似。另外我们还通过以下方式使其更高效。